基于QR分解的MIMO-OFDM檢測(cè)算法的改進(jìn)

陳 磊，張 敏，趙瑞弟，王可霞

（遼寧工業(yè)大學(xué)電子與信息工程學(xué)院，遼寧錦州121001）

0 引言

隨著信息技術(shù)的發(fā)展，越來(lái)越多地需要高速率數(shù)據(jù)傳輸，無(wú)線通信技術(shù)也開(kāi)始不斷地向?qū)拵o(wú)線傳輸方向轉(zhuǎn)變，而MIMO技術(shù)[1]和OFDM技術(shù)[2]也已成為寬帶無(wú)線傳輸?shù)?個(gè)主體。將這2種技術(shù)結(jié)合的MIMO-OFDM系統(tǒng)可以實(shí)現(xiàn)很高的傳輸速率，并且能通過(guò)分集實(shí)現(xiàn)很強(qiáng)的可靠性，將會(huì)成為第4代通信發(fā)展的趨勢(shì)。MIMO-OFDM系統(tǒng)信號(hào)檢測(cè)算法的研究主要是在提高檢測(cè)器性能和降低檢測(cè)復(fù)雜度之間平衡。

1 系統(tǒng)模型

MIMO-OFDM系統(tǒng)[3]模型如圖1所示。發(fā)射天線數(shù)為N，接收天線數(shù)為M。在發(fā)射機(jī)中，信源輸出經(jīng)串并變換和映射等處理后，形成N層并行數(shù)據(jù)流，每層數(shù)據(jù)再串并變換，然后進(jìn)行IFFT，再經(jīng)過(guò)并串變換和加循環(huán)前綴后送入發(fā)射天線，發(fā)射信號(hào)經(jīng)頻率選擇性多徑衰落信道到達(dá)M個(gè)接收天線，在接收端對(duì)各接收信號(hào)先去循環(huán)前綴，再經(jīng)串并變換和FFT[4]等相反操作后將信號(hào)送入檢測(cè)器檢測(cè)并輸出。

圖1 MIMO-OFDM系統(tǒng)模型

接收機(jī)收到的信號(hào)矢量為:

式中，X=[X1…XN]T，Y=[Y1…YM]T和W=[W1…WM]T分別為發(fā)送信號(hào)矢量、接收信號(hào)矢量和高斯白噪聲;H=[Hmn]為復(fù)數(shù)域上M×N矩陣，Hmn（n=1，…，N，m=1，…，M）表示從發(fā)射天線n到接收天線m間的信道頻響系數(shù)。

2 基本算法原理

2.1 最大似然（ML）檢測(cè)算法

最大似然檢測(cè)算法[5]是最佳檢測(cè)算法，其基本思想是:在所有可能的發(fā)送信號(hào)矢量集中遍歷搜索，得到使似然函數(shù)最大的信號(hào)向量，將其作為估計(jì)。假設(shè)所有的未編碼符號(hào)都是等概率發(fā)送的，那么ML檢測(cè)算法為:

式中，Ω表示所有可能的發(fā)送信號(hào)矢量;‖Y－HX‖表示它的歐式距離。

2.2 迫零（ZF）檢測(cè)算法

迫零檢測(cè)算法的基本思想是:把信道矩陣H帶來(lái)的干擾強(qiáng)制為零，所以被稱作迫零算法[6]。它是空時(shí)信號(hào)處理接收算法中最簡(jiǎn)單的一個(gè)。ZF檢測(cè)算法的加權(quán)矩陣為:

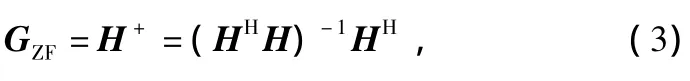
式中，（·）H表示矩陣的Hermitian矩陣;（·）+表示矩陣的廣義逆矩陣。將加權(quán)矩陣GZF乘以式（1），可以得到:

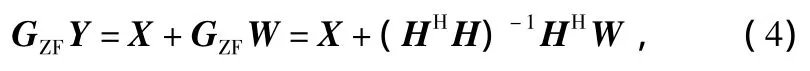
忽略噪聲的影響，得到X的估計(jì)

2.3 最小均方誤差（MMSE）檢測(cè)算法

ZF檢測(cè)算法在抑制信號(hào)干擾時(shí)忽略了噪聲對(duì)系統(tǒng)性能的影響，而MMSE檢測(cè)算法則不然。MMSE檢測(cè)算法可使由噪聲和同頻信號(hào)相互干擾造成的錯(cuò)誤達(dá)到最小。它雖然降低了信號(hào)分離的質(zhì)量，但具有較好的抗噪性能。其基本思想是:使判決統(tǒng)計(jì)矢量和發(fā)送信號(hào)X之間的均方誤差最小。MMSE檢測(cè)算法的加權(quán)矩陣為:

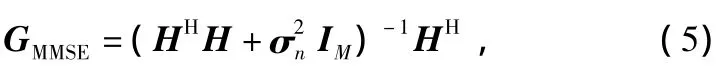
與式（1）相乘后得到:

2.4 串行干擾抵消（SIC）檢測(cè)算法

干擾抵消算法是一個(gè)迭代過(guò)程。SIC檢測(cè)算法[8]的思想是:采用一種復(fù)雜度不高的線性檢測(cè)算法（ZF或MMSE），解調(diào)出一個(gè)天線上的數(shù)據(jù)，再消除解調(diào)出的符號(hào)在接收信號(hào)中對(duì)其他層的干擾，再用同樣的方法，依次對(duì)其他天線上的發(fā)送符號(hào)進(jìn)行線性檢測(cè)和干擾抵消，直到估計(jì)出所有發(fā)送信號(hào)。

2.5 基本QR檢測(cè)算法

將信道矩陣HN×M進(jìn)行QR分解:

式中，QN×M是酉矩陣[9]，RM×M是一個(gè)上三角矩陣。通過(guò)將信道矩陣QR分解，得到接收向量的每一個(gè)分量，表示如下:

由于R具有上三角性質(zhì)，因此可以從最底層開(kāi)始得到各層發(fā)送信號(hào)的估計(jì)量，每層判決信號(hào)表示如下:

3 改進(jìn)的QR算法

3.1 循環(huán)迭代QR算法

先對(duì)接收向量H進(jìn)行一次QR分解，得到發(fā)射信號(hào)的估計(jì)向量。而最后檢測(cè)層的分集增益最大，所以只判定輸出性能最好的，其余各層的信息丟棄不用。接下來(lái)進(jìn)行第2次檢測(cè)，為了讓第1次最后檢測(cè)出的放到第1層檢測(cè)，需要對(duì)信道矩陣H的列進(jìn)行調(diào)整，然后再進(jìn)行QR分解。因?yàn)闄z測(cè)時(shí)第1層的信息是第1次檢測(cè)的結(jié)果，所以不用再判決。重復(fù)這個(gè)過(guò)程，直到檢測(cè)出所有層的符號(hào)。循環(huán)迭代QR分解檢測(cè)算法[10]的具體檢測(cè)步驟如下:

①對(duì)H進(jìn)行第1次QR分解，得到估計(jì)向量

③循環(huán)調(diào)整H的列向量:h1→hM→hM－1→…→h2→h1，即將第1列的向量移動(dòng)到最后一列，其余各列依次往前移動(dòng)一列。假設(shè)調(diào)整后新的信道矩陣為

④將進(jìn)行QR分解并檢測(cè)下面M－1層的信號(hào)，只保留最好檢測(cè)層結(jié)果;

⑥通過(guò)新的檢測(cè)，得到新的檢測(cè)序列:

4發(fā)4收循環(huán)迭代QR檢測(cè)的過(guò)程如表1所示。

表1 4發(fā)4收循環(huán)迭代QR檢測(cè)過(guò)程

其中，H為信道增益矩陣;Y為接收端向量;X為發(fā)射端向量為第1次檢測(cè)結(jié)果為最終檢測(cè)結(jié)果。

3.2 IC_QR_LI算法

IC_QR_LI算法是在循環(huán)迭代QR檢測(cè)算法的第1次QR算法之前先排序，無(wú)論是QR算法還是循環(huán)迭代QR算法，都有一個(gè)共同的缺點(diǎn)，就是有誤差累計(jì)，即最先檢測(cè)層產(chǎn)生的誤差會(huì)影響到后續(xù)檢測(cè)的準(zhǔn)確度，現(xiàn)在在第1次QR分解之前先進(jìn)行排序，使得在進(jìn)行QR檢測(cè)時(shí)最先檢測(cè)層是信噪比最高的那一層，這樣誤差的累計(jì)就會(huì)有效地降低。本文只進(jìn)行了一次排序，所以說(shuō)算法復(fù)雜度幾乎沒(méi)有增加，而性能的提高相比于復(fù)雜度的增加卻是相當(dāng)可觀的。

4 計(jì)算機(jī)仿真結(jié)果分析

仿真條件:MIMO系統(tǒng)的發(fā)送端天線數(shù)為4，接收端天線數(shù)也為4，收發(fā)均采用線性天線陣列，調(diào)制方式采用BPSK，收發(fā)之間存在理想的反饋信道。

采用循環(huán)迭代和不采用循環(huán)迭代的性能曲線如圖2所示。采用循環(huán)迭代QR檢測(cè)的性能比不采用循環(huán)迭代的性能要好很多。當(dāng)然，性能的大幅提高也付出了算法復(fù)雜度增加的代價(jià)，4×4的MIMO系統(tǒng)采用循環(huán)迭代QR檢測(cè)算法，要經(jīng)過(guò)4次QR分解，復(fù)雜度是基本QR算法的4倍。采用預(yù)先排序和不采用預(yù)先排序的性能曲線如圖3所示。采用了預(yù)先排序后檢測(cè)的性能有了提高，而復(fù)雜度方面增加的運(yùn)算量只有一次排序所需要的運(yùn)算量。

圖2 VBLAST系統(tǒng)QR檢測(cè)算法采用循環(huán)迭代和不采用循環(huán)迭代的性能比較

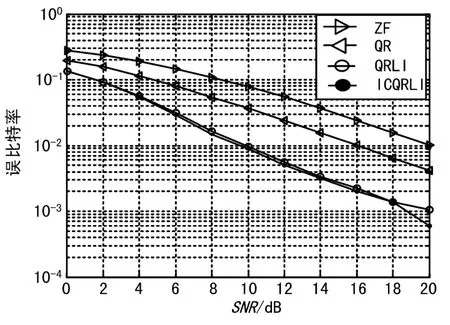
圖3 VBLAST系統(tǒng)QR檢測(cè)算法采用排序和不采用排序的性能比較

5 結(jié)束語(yǔ)

提出了一種改進(jìn)的QR檢測(cè)算法，并利用MATLAB進(jìn)行了仿真，比較了該算法與基本QR算法的性能。通過(guò)仿真可以看出，與基本QR算法和循環(huán)迭代QR檢測(cè)算法相比，基于預(yù)先排序的循環(huán)迭代檢測(cè)算法的性能是最好的，計(jì)算復(fù)雜度并沒(méi)有增加很多，并且實(shí)現(xiàn)了檢測(cè)性能和復(fù)雜度之間很好的平衡。

[1]GORVAJA R，ARMADA A G.Effect of Multipath and Antenna Diversity in MIMO-OFDM Systems with Imperfect Channel Estimation and Phase Noise Compensation[J].Physical Communication，2009，1（4）:288－297.

[2]胡茂凱，陳西宏，孫際哲，等.改進(jìn)時(shí)變多徑信道下OFDM系統(tǒng)性能分析[J].華中科技大學(xué)學(xué)報(bào)，2012，40（10）:2－3.

[3]饒文元，王軍選.貝爾實(shí)驗(yàn)室分層空時(shí)結(jié)構(gòu)和空時(shí)編碼[J].電信快報(bào)，2004（3）:1－3.

[4]JIA Dan-ping，YUAN Zhuo，SAN Hong-li.The Study of Fluorescence Thermal Measurement Based on DSP [J].Procedia Engineering，2012，29:2864－2868.

[5]CHO Yongsoo，KIM Jaekwon，YANG Wonyoung，et al.MIMO－OFDM Wireless Communications with MATLAB[M].USA:John.Wiley ＆ Sons，2010.

[6]WANG Shi-liang，SUN Song-lin，JING Xiao-jun.Tree Pruning for MIMO Sphere Detection Based on MMSE Detection[J].The Journal of China Universities of Posts and Telecommunications，2012，19（4）:64－72.

[7]FENG Xing-le，ZHU Shi-hua，REN Pin-yi.Transmit Antenna Selection in V-BLAST System[J].Journal of Electronics，2005，23（4）:1－2.

[8]付翠竹.MIMO SIC檢測(cè)合并技術(shù)[J].現(xiàn)代電信科技，2011（5）:1－2.

[9]CHENG Jing，HE Cheng-yuan.Some Properties of Generalized Unitary Matrices and Generalized Hermite Matrices[J].Journal of Chongqing Normal University，2010，27（3）:58－61.

[10]劉海濤，孫宇昊，李冬霞，等.基于QR分解的循環(huán)迭代檢測(cè)算法[J].電波科學(xué)學(xué)報(bào)，2005，20（5）:2－3.