應用Poisson板理論求解S0蘭姆波在通孔缺陷的散射

張海燕，姚杰聰，馬世偉

(1. 上海大學通信與信息工程學院，特殊光纖與光接入網省部共建重點實驗室，上海 200444；2. 上海大學機電工程與自動化學院，上海市電站自動化技術重點實驗室，上海 200072)

0 引 言

因為蘭姆波在(NonDestructive Testing, NDT)應用的潛力，近年來波導中的散射問題受到相當大的關注。由于其復雜性，所進行的研究主要是應用數值方法如有限元法(Finite Element Method, FEM)[1]或邊界元法(Boundary Element Method, BEM)[2]。雖然二維(2D)研究能夠部分洞察蘭姆波與缺陷之間的相互作用，為了全面地理解散射過程，3D建模是必須的。盡管計算能力和效率不斷提高，數值方法仍然需要相當高的計算代價。即使高性能計算機，對一個特定的入射波場，計算時間也是幾個小時的數量級。而解析或半解析解對這樣的問題是適用的，能夠快速仿真眾多不同散射體的散射。對于2D問題，解析解方法已用于研究蘭姆波遇圓形腔體[3]或裂紋[4]的散射。對于3D問題，尋求解析解相當復雜。雖然瑞利-蘭姆波解是精確的，然而，它在表征蘭姆波與結構缺陷的作用時相當困難，因為在無限多的模式中，需要考慮模式耦合的影響[5-8]。即使激發頻率低于第一階模式的截止頻率(也即僅有一個傳播模式)，近場波高階模式[9]在缺陷與周圍結構的界面上也參與模式轉換過程[10]。Grahn[6]采用雙級數波函數展開法，給出了部分穿透孔的數值解，發現為了實現收斂，需要大量的蘭姆波模式。例如，在第二個彎曲模式的1/3倍截止頻率這樣低的頻率，計算中需要9個蘭姆波模式[11]。對于更高的頻率，在展開式中將會有更多項，這樣將導致很慢的收斂率。因此，要求尋找計算上更有效的求解方法。

作為對蘭姆波精確解的替代，各種近似板理論，如 Kane-Mindlin膨脹形變(extensional deformation)理論[12]以及 Mindlin板彎曲理論[13]，無論是對稱和反對稱模式，都已可以很精確地描述蘭姆波的頻散特性，達到了第二個彎曲模式的截止頻率[14]。在低頻限制下，對于膨脹波(S0波)，Mindlin板理論退化到 Poisson板理論，對于彎曲波(A0波)，Mindlin板理論退化到 Kirchhoff板理論。Mckeon和Hinders[15]采用Mindlin板理論，考察了S0波與各種尺寸孔的散射特征。對點源激發的 S0波，證實了當孔的尺寸大于波束尺寸時，散射的影響很重要，解釋了鋁板中大缺陷孔平行投影層析成像中存在星狀條紋圖案贗像的原因，文中的理論和散射求解方法對發展蘭姆波衍射層析成像具有重要作用。

本文基于Poisson板理論，研究了入射的S0平面波與圓形通孔缺陷之間的相互作用。由于所考慮的問題是3D問題，散射場中也包含SH波。又因為入射場關于板中面是對稱的，散射體也是對稱的，在低頻時，散射場中僅包含對稱的S0和SH0模式，文中對這兩種模態的散射特性進行了研究，并與Diligent的3D精確理論[5]進行比較。給出了這兩個模式位移散射場的遠場方向圖，研究了激發頻率和缺陷尺寸對散射結果的影響，希望能為蘭姆波無損檢測提供一些理論指導。

1 問題描述

考慮入射的 S0平面波遇到圓形通孔缺陷的散射。幾何模型如圖1所示，板的厚度為2h，通孔的半徑為a，坐標系統原點位于通孔的中心。考慮時諧狀態，省略時間因子exp(i)tω?，其中ω表示角頻率，t表示時間。

2 Poisson板理論

2.1 基本方程

Poisson板理論是描述膨脹運動的低階近似板理論。其位移場是由兩個標量勢場φ、ψ控制，在固定頻率下，兩者滿足亥姆霍茲(Helmholtz)方程：

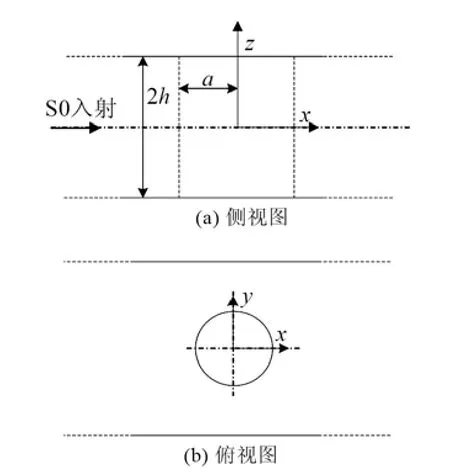
圖1 含通孔板幾何模型Fig.1 The geometry of plate with a through hole

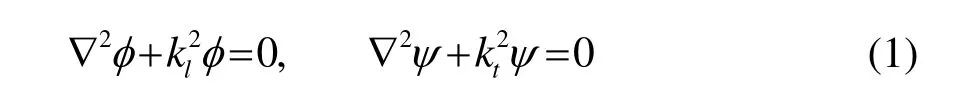
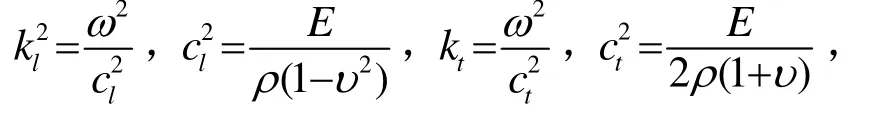
圖2給出了Poisson板理論與3D精確理論頻散曲線的比較。Poisson板理論的cl在低頻時與S0模式重合，Poisson板理論的ct在整個頻率范圍內與SH0模式重合。在低于S1模式的截止頻率(頻厚積約為2.8 MHz·mm)，S0和SH0是3D精確理論中的傳播模式，它們對波場的貢獻最大，其它非傳播模式(凋零波，波數為復數)相對于這兩個模式對波場的貢獻較小。因此，在與這兩個模式重合的頻率范圍內，Poisson板理論可以作為3D精確理論的一種近似替代。

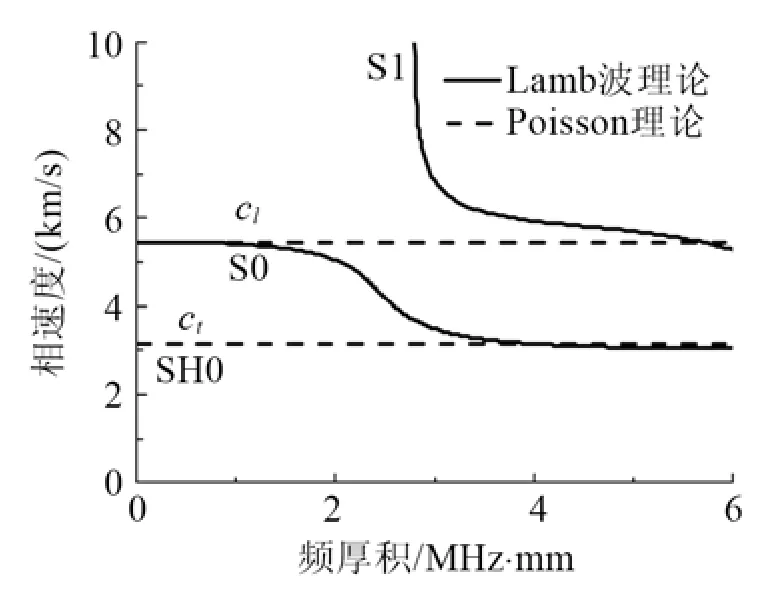
圖2 Poisson板理論與3D精確理論頻散曲線的比較Fig.2 Dispersion curves of the Poisson theory (dash lines) compared to the exact 3D theory (solid lines)

柱狀坐標下的應力和應變可表示為[6]：

式(3)中的位移用勢函數表示為

結合式(2)~(4)，可得：

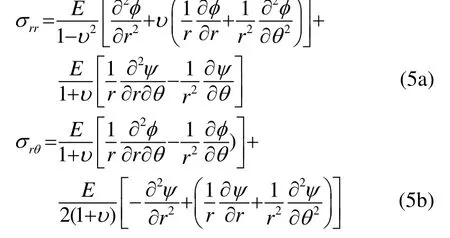
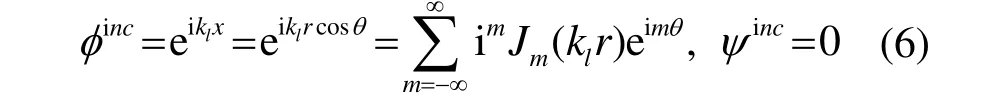
2.2 波場展開

S0平面波入射時，入射場用勢函數表示為：

將式(6)代入式(5)，可得

在散射場區域，方程(1)的解為

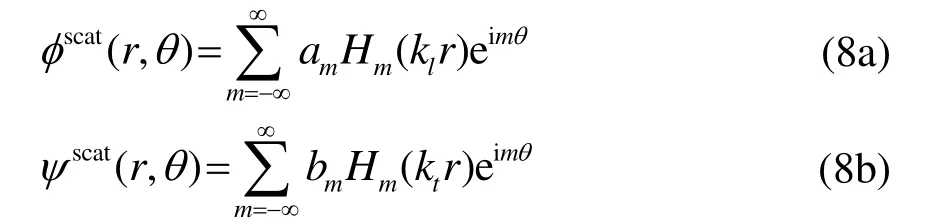
am與bm為散射場的展開系數，可利用在缺陷處的邊界條件求出。

將式(8)代入式(5)，可得

2.3 邊界條件

同3D精確理論類似，在孔邊緣r=a處的邊界條件為：

方程(8)中的展開系數可通過式(10)確定。對每一個m值，含有兩個未知數的系統方程用矩陣形式表示為

式(11)中的αi,j(i,j=1,2)、βi(i= 1 ,2)見后面附錄。

3 數值計算

數值示例中所用的材料為剛板，其材料參數為：楊氏模量E=210GPa，泊松比υ=0.3，或Lamé常數λ=121.2 GPa，μ=80.8 GPa，密度ρ=8100 kg/m3。

數值分析中的無量綱參數為：入射場的波數k與孔半徑的乘積ka(k為入射的S0模式的波數，這里k=kl)，歸一化頻率Ω=ωh/ct，孔半徑a/h。

文獻[5]給出了Poisson板理論和Diligent的3D精確理論在不同頻率、不同孔徑時兩種基本對稱模式的位移遠場散射方向圖，并對其結果進行了比較。散射波的位移遠場幅值定義為

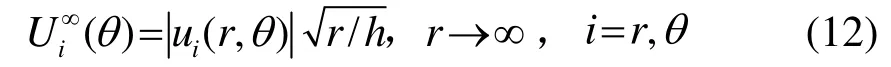
3.1 頻率變化對散射場的影響

圖3 不同頻率時S0模式的位移散射遠場方向圖Fig.3 Far field patterns of displacement scattering for S0 mode at different frequencies

圖4 不同頻率時SH0模式的位移散射遠場方向圖Fig.4 Far field patterns of displacement scattering for SH0 mode at different frequencies

圖3和圖4給出了S0和SH0的位移散射遠場方向圖，其中，ka=1(a≈λ/6，λ為入射波的波長)。可以看到，隨頻率(更確切地說，頻厚積)增加，Poisson板理論偏離3D精確理論的變化情況。低頻時，Ω≤0.4，兩個理論模型具有完好的一致性。隨著頻率增加，兩者間逐漸分離，當Ω=1.2時，Poisson板理論與3D精確理論的偏差較小。但隨著頻率繼續增大，Poisson板理論在形狀上與3D精確理論的差異逐漸增大。對不同的孔徑，如ka=2(a≈λ/3)，隨著頻率變化，這兩個理論具有類似的變化趨勢，只不過它們出現偏離時的頻率可能不同，這里不再給出。

3.2 缺陷尺寸對散射場的影響

既然Poisson板理論在低頻情況下可以作為3D精確理論的替代，我們可以在低頻時采用 Poisson板理論研究散射體(缺陷)變化對散射場的影響，以便對缺陷進行評價，這將大大簡化計算。圖5和圖6給出了Ω=0.4，不同ka值時的S0和SH0模式的位移散射遠場方向圖。可以看到，散射的 S0波主要集中在前向(0°)和后向(180°)(圖5)，而散射的 SH0波主要集中在橫向方向(90°~150°,210°~270°)(圖6)。隨著ka增大，S0波越來越集中在前向，且具有更強的波束指向性和更大的幅值(圖5)。同樣，隨ka增大，SH0波在橫向方向也具有更大的幅值(圖6)。更清晰的比較顯示在圖7中，可以看到，0°散射角時的S0散射波幅值可以反映ka的變化，而110°(或 250°，由于對稱性，圖中未給出)附近散射角時SH0散射波的幅值也可以反映ka的變化，且這種變化近似線性，如圖7(b)、7(d)所示，以此可以對缺陷的大小進行評判。

圖5 Ω=0.4，不同ka值時S0模式的位移散射遠場方向圖Fig.5 Far field patterns of displacement scattering for S0 mode at Ω= 0 .4 for different ka values

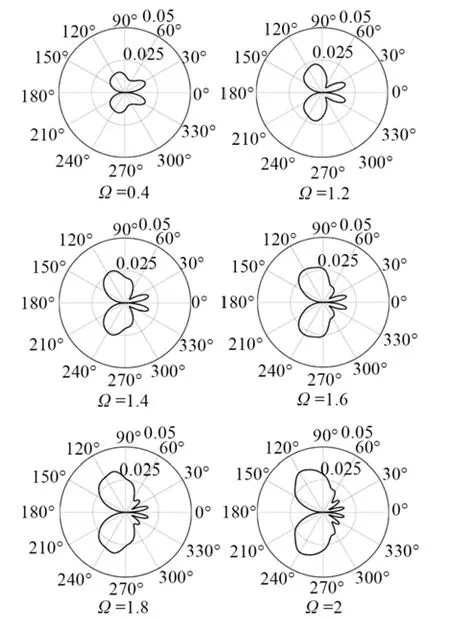
圖6 Ω=0.4，不同ka值時SH0模式的位移散射遠場方向圖Fig.6 Far field patterns of displacement scattering for S0 mode at Ω= 0 .4for different ka values

圖7 Ω =0.4，不同ka值時S0和SH0模式的散射圖Fig.7 Scattering patterns of S0 and SH0 modes for different ka values atΩ=0.4

4 結 語

盡管3D精確理論在高頻情況下求解散射場比較精確，但是其計算過程繁瑣，并且隨著頻率的增高，模態數變多，計算復雜性變大。在低頻情況下，采用3D精確理論并沒有顯示出優越性。基于此，本文用簡單的Poisson板理論計算S0蘭姆波對通孔的散射，并與 3D精確理論進行了對比，給出了Poisson板理論的適用范圍。在此基礎上，對S0和SH0的遠場散射特性進行了研究，得出的結論是：

(1) Poisson板理論是最低階的描述膨脹波運動的近似板理論，僅在低頻下(如對鋼板，Ω≤0.4，相當于頻厚積≤0.4MHz·mm)才可以給出較精確的結果。

(2) 在低頻限制下，Poisson板理論相比3D精確理論是一種較好的選擇，可以極大地簡化計算。這是因為3D精確理論波場展開式中包含較多的傳播模式和非傳播模式，而 Poisson板理論僅含有兩個模式。實際上，為了避免蘭姆波的頻散和多模式混疊，蘭姆波檢測多在低頻情況下進行。

(3) S0和SH0具有不同的散射場分布。S0散射波能量主要集中在前向和后向，其前向散射波幅度隨孔徑增大線性增加。SH0散射波能量主要集中在橫向方向，在某些散射角度方向散射波幅值也隨孔徑呈近似線性變化。這兩種模式都可以為缺陷無損評價提供理論指導。

(4) 本文所用的理論和方法為用解析法求解蘭姆波在固體中的散射提供了基礎。從入射場來說，可以推廣到任何可能的波型，如更高階的對稱模式、彎曲波模式(反對稱模式)，也可以從平面波入射推廣到點源、有限寬度的源入射。從缺陷類型來說，可以從通孔推廣到盲孔，也可以從圓孔推廣到橢圓孔，甚至不規則孔。從材料來說，也可從各向同性材料推廣到各向異性復合材料。

參考文獻

[1] 鄭陽, 何存富, 周進節, 等. 超聲蘭姆波斜入射裂紋時的散射特性[J]. 機械工程學報, 2013, 49(4): 6-12.ZHENG Yang, HE Cunfu, ZHOU Jinjie, et al. Scattering characteristic of Lamb wave at crack with oblique incident[J]. J. Mech.Engin., 2013, 49(4): 6-12.

[2] 王坤, 黃松齡, 趙偉. 平板蘭姆波與缺陷作用邊界元仿真實現研究[J]. 中國機械工程, 2009, 20(8): 887-891.WANG Kun, HUANG Songling, ZHAO Wei. Study on implementation of boundary element method simulation for Lamb wave interaction with defects in elastic plate[J]. China Mechanical Engineering, 2009, 20(8): 887-891.

[3] WANG X, YING C F. Scattering of Lamb waves by a circular cylinder[J]. J. Acoust. Soc. Am., 2001, 110(4): 1752-1763.

[4] Castaings M, Clezio E L, Hosten B. Modal decomposition method for modeling the interaction of Lamb waves with cracks[J]. J.Acoust. Soc. Am., 2002, 112(6): 2567-2582.

[5] Dilligent O, Grahn T A, Bostr?m A, et al. The low-frequency reflection and scattering of the S0Lamb mode from a circular through-thickness hole in a plate: Finite Element, analytical and experimental studies[J]. J. Acoust. Soc. Am., 2002, 112(6):2589-2601.

[6] Grahn T. Lamb wave scattering from a circular partly through-thickness hole in a plate[J]. Wave Motion, 2003, 37: 63-80.

[7] 鄧慶田, 楊智春. 導波在多損傷結構中的散射[J]. 振動與沖擊,2010, 29(4): 40-43.DENG Qingtian, YANG Zhichun. Scattering of guided waves in a plate with multiple damages[J]. Journal of Vibration and Shock,2010, 29(4): 40-43.

[8] Moreau L, Caleap M, Velichko A, Wilcox P D. Scattering of guided waves by flat-bottomed cavities with irregular shapes[J].Wave Motion, 2012, 49: 375-387.

[9] Doyle J F. Wave propagation in structures[M]. Second Edition,New York: Springer, , 1997.

[10] Wang C H, Rose L R F. Wave reflection and transmission in beams containing delamination and inhomogeneity[J]. J. Sound. Vib.,2003, 264: 851-872

[11] Wang C H, Chang F K. Scattering of plate waves by a cylindrical inhomogeneity[J]. J. Sound. Vib., 2005, 282: 429-451.

[12] Kane T R, Mindlin R D. High-frequency extensional vibrations of plates[J]. J. Appl. Mech., 1956, 23: 277-283.

[13] Mindlin R D. Influence of rotary inertial and shear on flexural motions of isotropic, elastic paltes[J]. J. Appl. Mech., 1951, 18:31-38

[14] Wang C H, Rose L R F. Wave reflection and transmission in beams containing delamination and inhomogeneity[J]. J. Sound. Vib.,2003, 264: 851-872.

[15] Mckeon J C P, Hinders M K. Lamb wave scattering from a through hole[J]. J. Sound. Vib., 1999, 224(5): 843-862.