不同底質海底窄帶混響信號空間相關半徑研究

韓榮榮，孫 輝，朱廣平，張明輝，劉 剛

(哈爾濱工程大學水聲技術重點實驗室，黑龍江哈爾濱 150001)

0 引 言

混響是海洋中大量無規則散射體對入射信號產生的散射波在接收點上接收到的所有散射波的總和。其信號具有動態范圍大、與發射信號相關性較強等特點[1]。在主動聲吶檢測中，海底混響是沉底目標探測的主要干擾，因此分析海底混響的特征對聲吶抗海底混響技術的研究具有重要意義。混響仿真的主要方法有兩種，一種是根據混響信號的概率分布，仿真所需分布的混響信號[2,3]；另一種是單元散射模型，即將海底劃分為小散射單元，計算每個單元的散射信號在接收點的迭加得到混響信號[4-6]。本文進行海底混響的仿真時基于比較成熟的單元散射模型，使用網格化的方法對海底有效散射區域進行劃分，對不同海底底質混響信號的相關半徑進行研究。使用此模型來仿真海底混響信號，其物理意義明確，能得到混響在不同位置的空間相關性，可以作為抑制海底混響研究的基礎。

單元散射模型是將海底劃分為小散射單元，每個散射單元的散射系數服從一定的規律，計算每個單元的散射信號在接收點的迭加來得到海底混響信號。可見，在單元散射模型中，如何劃分單元和單元的尺寸為此模型的關鍵。已有學者研究表明，海底混響信號的空間相關性隨海底散射系數相關半徑的增大而減小[7]，同時與海底底質特征有關[8]。

1 海底混響空間相關半徑的定義

用在鉛垂線上分開的兩個水聽器研究混響的空間相關性，證明海底混響比來自深水散射層的混響的相關性強得多。

混響的空間相關理論分析如圖1所示，兩水聽器之間相距為d，假設散射體是相互獨立的散射源，而且采用窄帶濾波，因此，散射源發出的聲波經散射體后，散射聲波在接收水聽器的輸出端可以看成是單頻簡諧波。當散射體到水聽器的距離r遠大于d時，分別寫出兩個水聽器處的散射波聲壓為

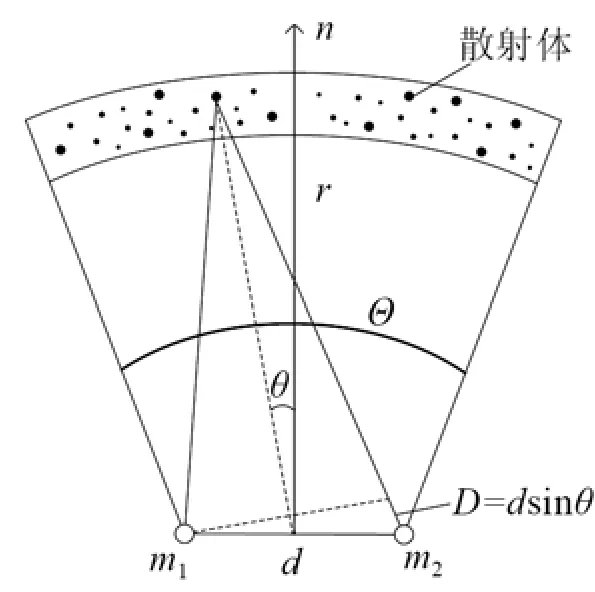
圖1 計算混響空間相關的示意圖Fig.1 Illustration of calculating reverberation spatial correlation

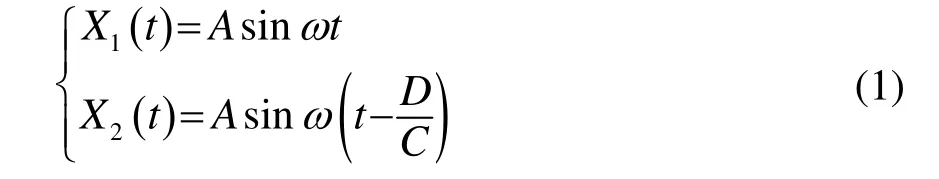
其中：ω為聲頻率，rad/s；C為介質中的聲速，m/s；A為混響聲壓的振幅；D為散射聲波傳播到兩水聽器之間的程差，m。

其中θ為散射體到兩個水聽器中心的連線和水聽器連線的法線n之間的夾角，rad。

于是有

由式(1)和(3)可得X1和X2之間的相關函數K為

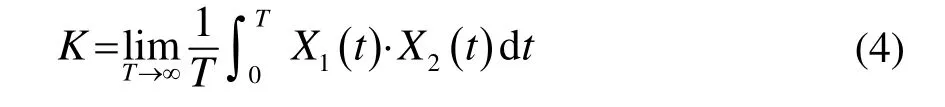
則其相關系數為

將式(1)和(3)代入式(5)中，可得

式中：k為波數，k=ωC。

元的作 則

考慮所有散射 用，

如果水聽器的水平指向性開角為Θ，本次實驗測得Θ≈23.5°，并有θ≤Θ，則sinθ≈θ

可見，當發射信號頻率一定時，混響場的空間相關系數和發射換能器的水平指向性開角有關，且隨水聽器間距的增大表現為振蕩衰減的形式，開角越大混響空間相關系數越大，如圖2所示。

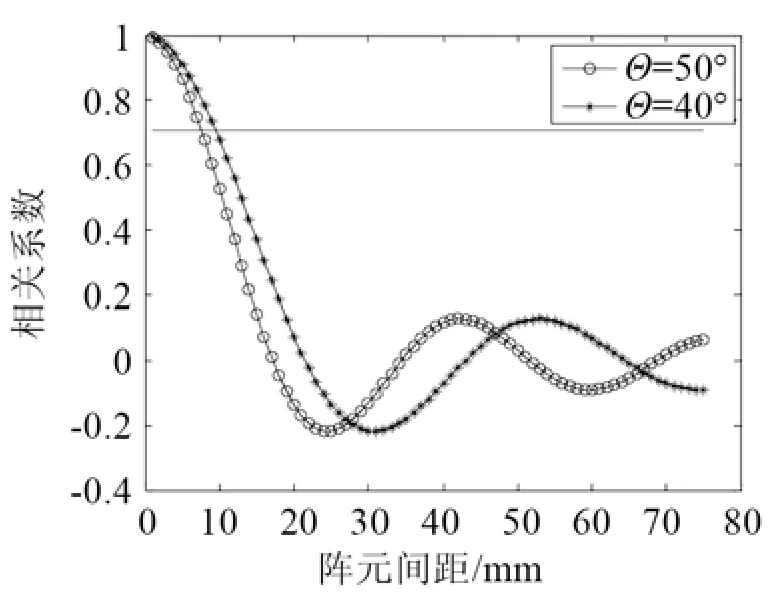
圖2 不同水平指向性開角Θ下混響相關系數Fig.2 The reverberation correlation coefficients of different horizontal beamwidths Θ

當發射換能器的水平指向性開角一定時，混響的空間相關系數僅和頻率有關，且隨水聽器間距的增大表現為振蕩衰減的形式，且頻率越高相關系數越小，如圖3所示。

圖3 不同頻率混響相關系數Fig.3 The reverberation correlation coefficients of different frequencies

理論上定義空間兩點混響信號的相關系數下降至 0.707時對應的距離為混響信號空間相關半徑，那么只要知道發射換能器開角和發射頻率，則混響信號空間相關半徑可以計算得到。但是實際上這里并沒有考慮到海底底質的實際情況，下面探討在海底不同底質的情況下，如顆粒大小與材質不同對混響信號空間相關半徑等的影響。

2 實驗測量不同海底底質的混響空間相關半徑

在不同海底底質的情況下，將海底顆粒簡單描述為如圖4所示的排列。圖4中不同的顆粒大小對應于不同的起伏與周期，這僅是海底散射體的其中一種可能的排列，并沒有數量級的精確描述。

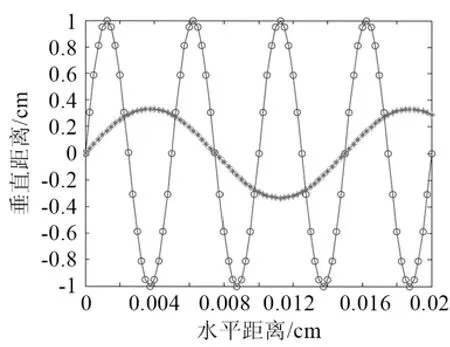
圖4 粗糙度不同海底底質起伏示意圖Fig.4 Illustration of seafloor sediment fluctuation for different roughnesses

本文在實驗中，選取三種不同的材質(顆粒大小不同)作為海底混響散射體，如圖5所示。對在這三種海底底質情況下的混響信號空間相關半徑和強度進行討論。

圖5 不同海底底質照片Fig.5 Photos of different seafloor sediments

實驗條件：發射信號頻率為100 kHz，經測量發射換能器在?3 dB處的水平指向性開角為47°。理論計算得到在此條件下混響的相關系數隨陣元間距的變化關系如圖6所示。

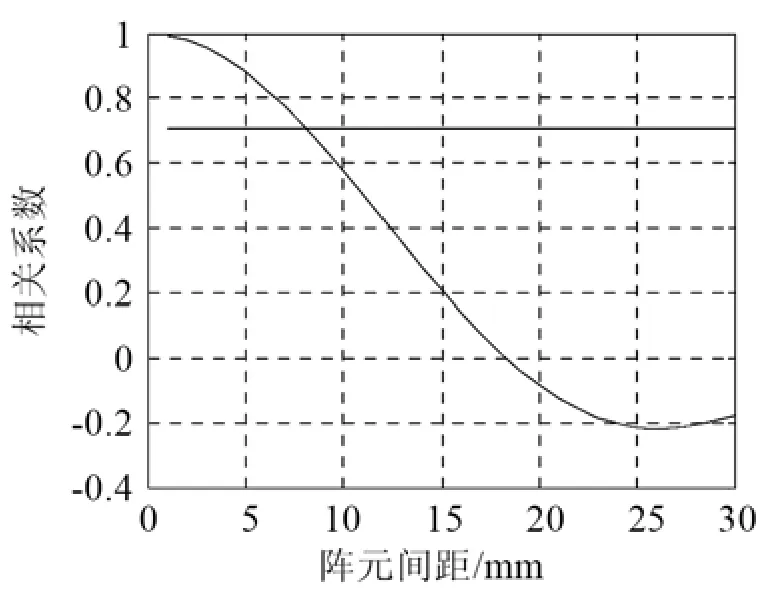
圖6 仿真混響相關系數隨陣元間距的變化Fig.6 The variation of the simulated reverberation correlation coefficient with the element separation

從圖6中可得在上述頻率和發射換能器條件下混響信號空間相關半徑的理論計算結果為8.1 mm。

在實際測量中，使用上述發射換能器，發射頻率為100 kHz，海底底質不同的散射體(如圖5)得到的混響信號空間相關系數與陣元間距的關系，如圖7所示。

圖7中，經測量得到細砂的混響空間相關半徑為7.28 mm，粗砂的混響空間相關半徑為4.03 mm，石頭的混響空間相關半徑為3.82 mm。上述實驗結果中，只有細砂混響空間相關半徑與理論計算得到的混響空間相關半徑相比擬。可見，理論計算混響空間相關半徑只與發射信號頻率和發射換能器的水平指向性開角有關是不夠的，還需要考慮海底底質的散射體顆粒大小。

實驗結果說明不均勻顆粒越大混響空間相關半徑越小。在上述各個散射體中細砂底較為平坦，粗砂與石頭底顆粒較大且不均勻，使得海底表面凹凸不平，在相同的空間距離得到的混響信號，起伏大的相關性弱，所以混響空間相關半徑就會相應地減小。

實驗數據表明，上述三種不同的散射體得到的混響信號的強度也有差別，其混響信號包絡如圖8所示。

在圖8中，點表示細沙的混響包絡，線是粗砂的混響包絡，虛線是石頭的混響包絡。可見，從石頭到細砂，其混響強度是依次增大的。證明發射換能器在此發射角度的情況下，不同材質的散射體產生的混響信號的強弱不同。

表1綜合描述了在海底為不同散射體時的相關半徑和混響強度的關系。

圖7 實測不同底質混響相關系數隨距離的變化Fig.7 The variations of the measured reverberation correlation coefficient with the element separation under different seafloor sediments

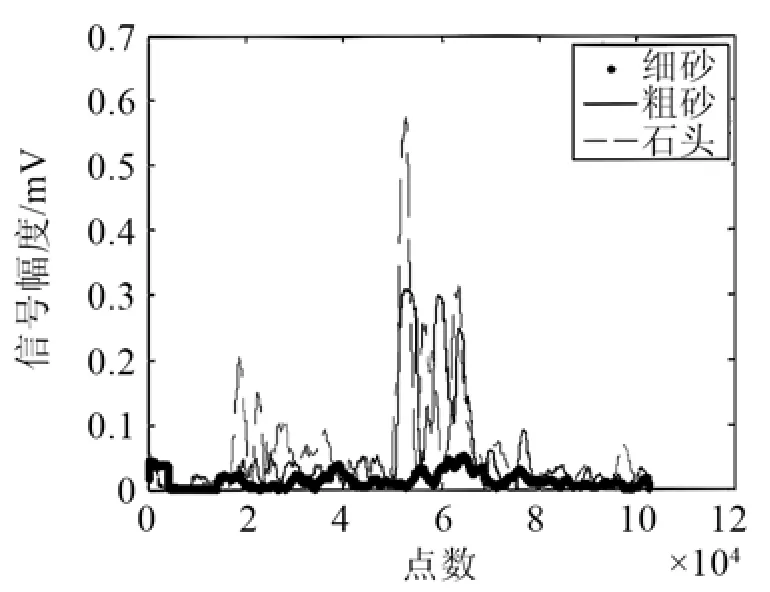
圖8 不同底質混響信號的包絡Fig.8 Envelopes of reverberation signals under different seafloor sediments

表1 不同海底底質的混響空間相關系數與混響強度Table 1 The reverberation spatial correlation coefficients and reverberation intensity under different seafloor sediments

3 結 論

本文在理論上計算了混響信號空間相關半徑，利用實驗數據與理論相結合，表明理論計算結果與實際情況中的細砂吻合較好，由于理論計算并沒有考慮到海底底質的不同，所以當不均勻的散射體顆粒增大時，混響空間相關半徑減小。為今后的抗混響技術研究提供理論基礎。

參考文獻

[1] 張蔚, 嚴勝剛, 劉建國. 主動聲吶均勻線列陣的混響仿真研究[J].計算機仿真, 2012, 29(8): 383-412.ZHANG Wei, YAN Shenggang, LIU Jianguo. Simulation research on reverberation for active sonar uniform linear array[J]. Computer Simulation, 2012, 29(8): 383-412.

[2] Abraham D A, Lyons A P, Reverberation envelope statistics and their dependence on sonar beamwidth[J]. IEEE Journal of Oceanic Engineering, 2004, 29(1): 126-137.

[3] Abraham D A, Lyons A P. Simulating non-rayleigh reverberation and clutter[J]. IEEE Journal of Oceanic Engineering, 2004, 29(2):347-362.

[4] V. V. 奧利雪夫斯基. 羅耀杰, 趙清, 武延祥, 譯. 海洋混響統計特性[M]. 北京: 科學出版社, 1977.Olshevskii V V. LUO Yaojie, ZHAO Qing, WU Yanxiang, translate. Statistical characteristics of sea reverberation[M]. Beijing:Science Press, 1977.

[5] 胡家福, 朱廣平, 張衛強. 收發分置聲吶淺海近程混響信號建模研究[J]. 海洋技術, 2012, 31(2): 27-31.HU Jiafu, ZHU Guangping, ZHANG Weiqiang. Modeling study on shallow sea short-range reverberation signal for bistatic sonar[J]. Ocean Technology, 2012, 31(2): 27-31.

[6] 方世良. 海洋混響信號的序貫仿真[J]. 聲學技術, 1996, 15(3):101-104.FANG Shiliang. Sequence simulation of oceanic reverberation signal[J]. Technical Acoustics, 1996, 15(3): 101-104.

[7] 朱燕, 陳剛, 魯辛凱. 水平分置海底混響信號的空間相關特性研究[J]. 艦船科學技術, 2009, 31(5): 56-59.ZHU Yan, CHEN Gang, LU Xinkai. Research on space correlation characteristic of horizontal biostatic seafloor reverberation signals[J]. Ship Science and Technology, 2009, 31(5): 56-59.

[8] 蒯多杰, 馮雷, 王長紅, 等. 不同底質混響空間相關函數仿真分析[J]. 聲學技術, 2007, 26(5): 1062-1063.KUAI Duojie, FENG Lei, WANG Changhong, et al. Reverberation simulation and analysis of different sediments using spatial correlation method[J]. Technical Acoustics, 2007, 26(5):1062-1063.