水下高速目標航行參數遙測技術研究

張慶國，王健培

(昆明船舶設備研究試驗中心，云南昆明 650051)

0 引 言

實時獲得水下目標的航行參數信息，有利于對其工作狀態進行監控，并能對其航行/攻擊性能進行精確評估。隨著高速輕型水下武器的不斷發展，如何實時獲得其航行參數信息顯得尤為重要。

隨著水聲技術的不斷發展，國內外學者對FSK、PSK、OFDM、PATTERN時延編碼和擴頻通信等技術進行了試驗研究，并取得了部分結果[1-6]。但是由于水聲信道的復雜性及其理解的局限性，現有水聲技術均具有一定的局限性，并非十分有效。因此，針對高速水下目標的航行參數遙測，進行試驗研究具有重要意義。本文對比分析了雙曲線調頻(Hyperbolic Frequency Modulation, HFM)與線性調頻(Linear Frequency Modulation, LFM)在水聲遙測上的特性，采用單頻信號(Continuous Wave, CW)與HFM信號組合調制的方式，進行高速水下目標的航行參數遙測技術與試驗研究。

1 調頻信號特性分析

研究表明，蝙蝠、海豚等哺乳生物采用了HFM形式的超聲信號進行定位與導航[2]，從生物進化擇優性上來看，HFM具有很高的實用性。HFM信號是一種多普勒不變信號，有時又稱為對數相位信號或線性周期信號[3]。為了便于特征分析，本文將HFM信號與水聲工程中常用的LFM信號進行對比分析。

1.1 HFM信號分析

HFM信號波形為：

式中：A為信號幅度；T為脈沖寬度；f0為中心頻率；m為調制參數。

由公式(1)可知，相位函數和瞬時頻率分別為：

假設存在如下關系：

由式(3)可知，k=f0t0。此時，將式(3)代入式(1)，可得到如下實信號計算公式：

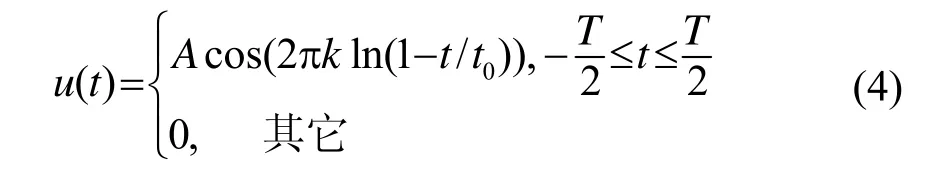
同理，將式(3)代入式(2)可得

假設信號幅度為A，脈沖信號寬度為T，上限頻率及下限頻率分別為fH、fL，fH=f(T/2)，fL=f( ?T/2)；調頻帶寬為B，B=fH?fL。算術中心頻率為fm，fm= (fL+fH)/2；時間中心頻率為f0，f0=f(0)；則式(5)中的參數k與t0分別為：

根據上述公式，產生HFM信號時域波形及時頻曲線波形如圖1所示。

1.2 LFM信號分析

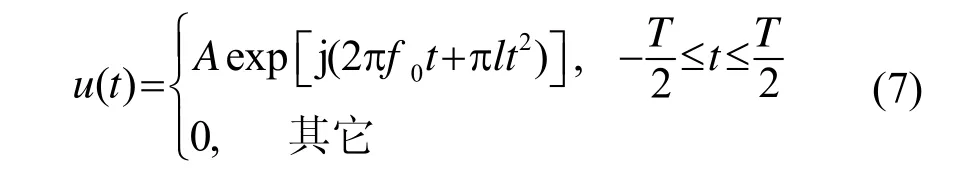
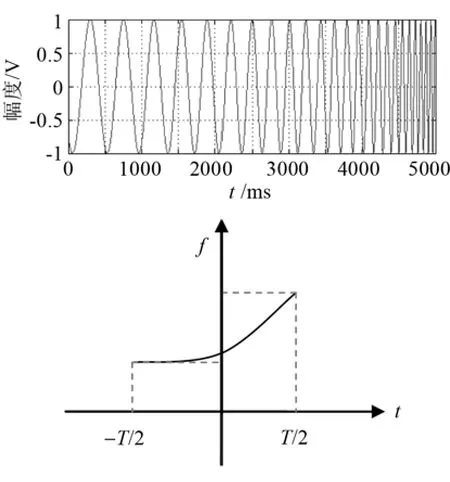
圖1 HFM信號時域波形及時頻曲線圖Fig.1 HFM signal waveform and time-frequency graph

LFM信號波形為：式中，A為信號幅度，f0為中心頻率，l為調頻斜率。

由式(7)可知，其相位函數和瞬時頻率分別為：

根據上述公式，產生 LFM 信號波形及時頻曲線波形如圖2所示。

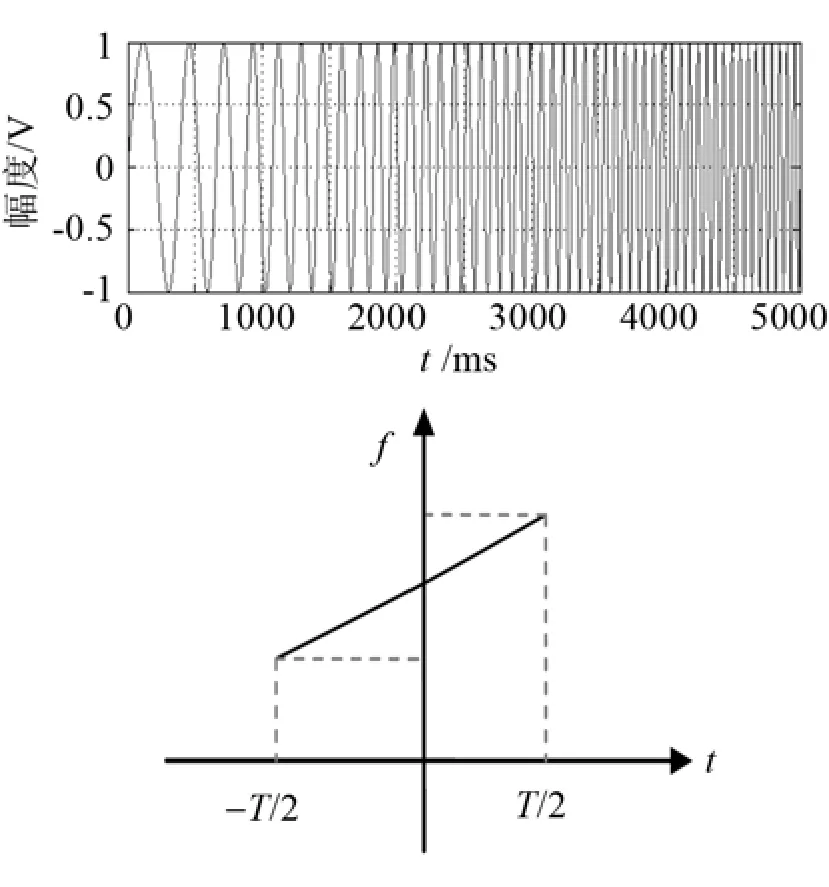
圖2 LFM信號時域波形及時頻曲線圖Fig.2 LFM signal waveform and time-frequency graph

1.3 多普勒特性比對分析

通常情況下，多普勒容限是指信號波形對速度或多普勒頻移敏感性的特征分量[4]。水聲信號的多普勒容限大小，直接影響著高速水下目標航行參數遙測功能與性能。

假設水下目標與接收端相對速度為v，聲速為c，則多普勒頻偏系數p= 1+v/c。那么對于HFM信號，在接收端收到的信號瞬時頻率存在如下關系：

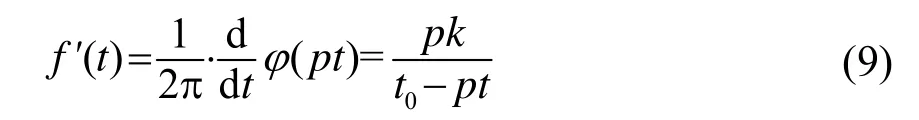
假設存在時延差 Δt，滿足如下關系：

將式(5)代入式(9)可推導出，當 Δt存在如下關系時，滿足式(10)。

由式(10)、(11)可以看出，對于HFM信號而言，多普勒壓縮效應等效于頻率調制函數在時間上的平移和在頻率上移動一個固定量，如圖3所示。

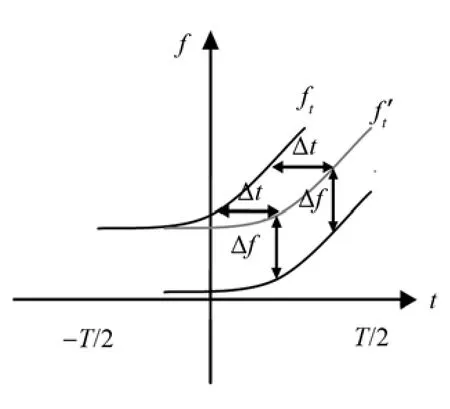
圖3 HFM信號在具有多普勒時瞬時頻率變化曲線圖Fig.3 Instantaneous frequency change of HFM signal with Doppler shift

由圖3可知，對于HFM信號的多普勒匹配，只需要改變參考波形的初始時間 Δt，便能與發射端的信號“完全”匹配。

同上，對于 LFM 信號存在相對速度時，接收端接收到的信號瞬時頻率為

由于找不到時延差 Δt來滿足式(10)，LFM信號的f'(t)不能通過平移與原f(t)相重合(不含p≈1時)，即 LFM 信號不具備多普勒不變性，而 HFM信號具有多普勒不變性。HFM信號經過水聲信道傳播后，接收端獲得的信號幅度不因與目標存在相對運動而劇烈變化，可最大程度上減少由于水下目標高速運動帶來的多普勒效應對水聲遙測的影響。

利用對數展開式對公式(1)進行展開如下：

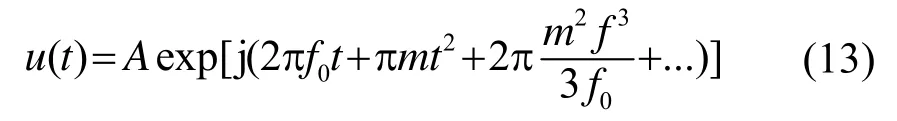
由式(13)可見，當忽略t3以上的各項后，便是LFM的計算公式，也就是說LFM信號是HFM信號的一種特例。

2 航行參數遙測信標波形結構設計

對于水下高速目標的航行參數遙測來說，信標波形的結構設計是其關鍵技術，直接影響水聲遙測基本功能及測量精度。本文采用CW信號與HFM信號相結合的方式組成同步式遙測信標。充分利用HFM信號的多普勒不變性，解決水下目標高速運動帶來的多普勒頻偏及幅度劇變等問題；同時利用CW信號對頻率的敏感性，來提高距離測量精度。所設計的信標波形結構如圖4所示。

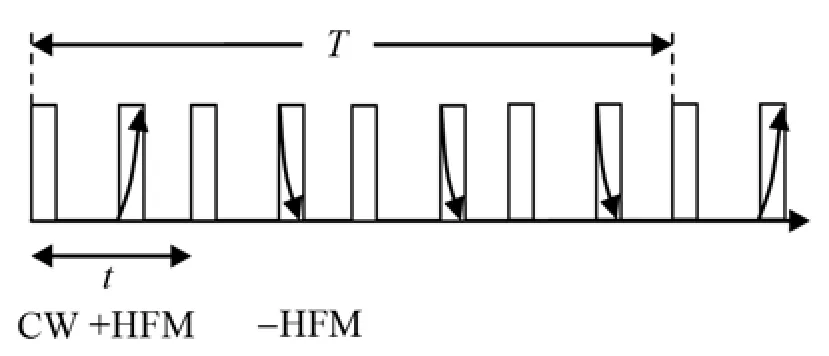
圖4 遙測信標波形結構示意圖Fig.4 Configuration of telemetry beacon signal

圖4中，T為測量周期，T=2 s；t為小周期，t=0.5 s。假設遙測參數(又稱姿態角)為：深度值、俯仰角、橫滾角和航向角，則分別對應于圖4中的四個組合脈沖信號。該信標主要性能為：水下目標最大速度不小于70 kn，水平測量半徑為3 km，姿態角度測量精度可達1°，深度值測量精度為0.5 m。由此可見，該信標可滿足大多數水下目標高速運動狀態下的航行參數測量要求。

3 實驗仿真分析

針對本文設計的遙測信標進行仿真分析。具體仿真參數為：CW 脈沖信號寬度為 5 ms，f0=75 kHz；HFM 信號調制寬度為 ± 3 .5 kHz，f0=75 kHz；T=2 s，t=40.96～81.92 ms(如圖4 所示)。

3.1 信標信號的可識別性仿真

該信標波形結構內共包含三種脈沖信號，即CW、+HFM、?HFM，為了防止在接收端產生混淆，需要各種信號相互之間具有較高的獨立識別性。將三種脈沖信號進行相關分析，歸一化相關圖如圖5所示。每種信號除自身相關峰明顯外，與其他信號相關特性均不明顯，也就是說該信標結構內的信號具有很好的獨立識別性，不存在識別模糊的問題。

3.2 多普勒效應仿真

圖5 信標波形內信號相關示意圖Fig.5 Normalized correlation function of the beacon signal

多普勒效應包括多普勒擴展和多普勒頻移。由于水聲信道的隨機、時變特性引起信號的多普勒擴展，在一般情況下約為0.1~0.7 Hz[5]，對水聲遙測影響不大，這里不予考慮，而多普勒頻移則是本文考慮的主要因素。

通常情況下，對于 LFM 信號采用中心頻率估計、相關樣本修正的方式進行多普勒頻偏修正，可滿足一般的水聲定位需求。但多普勒頻偏是隨著頻率的變化而非線性變化的，不能簡單地采用固定頻偏進行補償。另外，當水下目標速度較快時，按照常規方法，利用已知的 LFM 同步信號樣本對接收到的信號進行拷貝相關處理時，將會出現相關峰值下降、相關峰分裂等現象，最終降低了時延值測量的精度，甚至降低整個遙測系統精度。

以線性插值法[6]進行多普勒信號的模擬仿真，假設接收到的信號為x。分別將LFM和HFM信號進行中心頻率偏移的修正，將修正后的數據和x進行相關，從而獲得兩種信號在不同速度下的時延值偏移量，結果如圖6所示。

圖6 多普勒頻偏仿真比較圖Fig.6 Doppler shift simulation chart

從圖6中可以看出，在同樣的速度下，HFM信號的相關偏移量均小于 LFM 的相關偏移量，甚至在較大的相對速度下，HFM信號均能保持較高的時延值估計精度。這里為了實驗方便，該項仿真沒有考慮多途反射與疊加影響，在實際水聲信道環境下，其整體估計誤差將會增大，但整體規律相同。

4 湖上試驗

在某湖水域進行試驗，針對該種遙測信號波形的性能進行動態測試。在船只上安裝發射聲源，利用固定布放在水底的水聲基陣(接收端)進行信號接收，除驗證其遙測功能外，主要考察高速情況下的該聲信標信號存在多普勒偏移時，對水下目標的航行參數遙測所帶來的影響。

裝載發射聲源船速約 8~10 kn，聲源距離水下基陣約為750 m，其HFM的信號頻譜及相關性如圖7所示。實際HFM信號的長度為5 ms，經過水聲多途傳播后，擴展為7 ms左右，并存在多途信號相互疊加造成的幅度變化。從圖7中可以看出，即使在多途干擾及水面反射疊加的復雜水聲環境下，依然具有良好的識別特性。

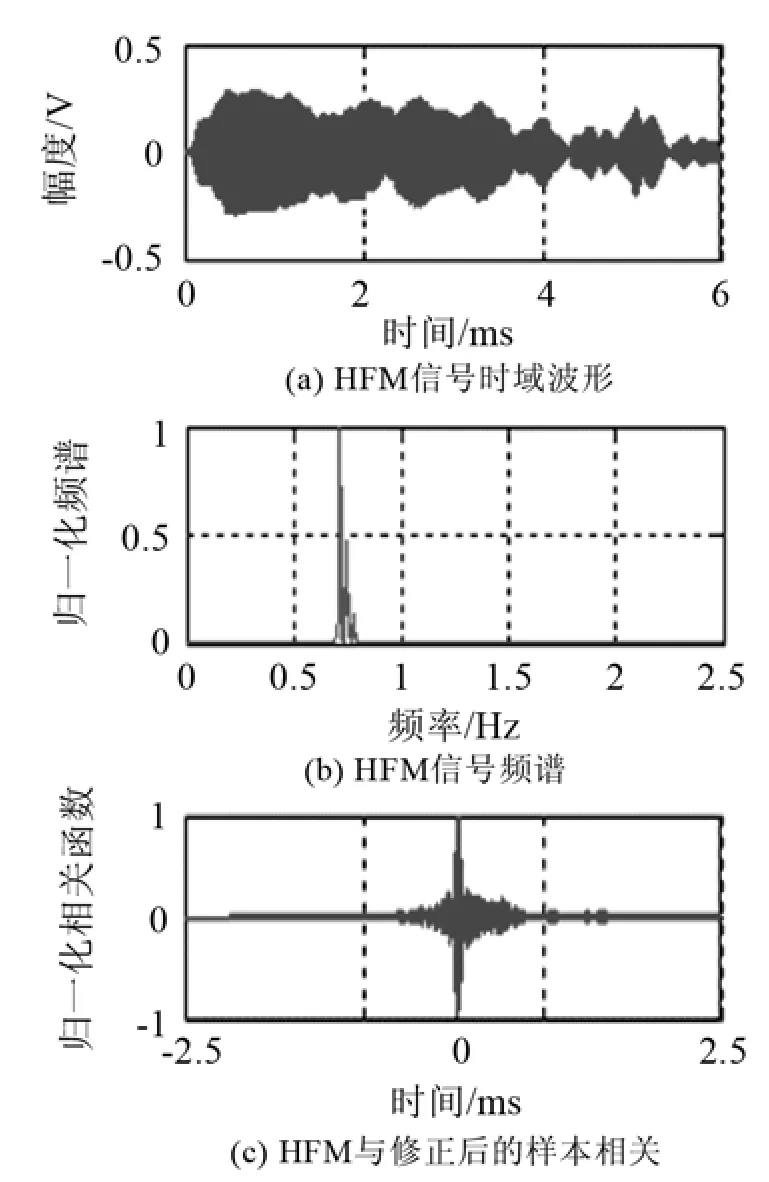
圖7 HFM信號經過水聲信道后的波形、頻譜和相關函數Fig.7 Waveform, spectrum and correlation function of the HFM signal after passing through the underwater acoustic channel

同上，當速度為8~10 kn，距離為800 m時，其 LFM 信號經過水聲信道后的信號頻譜及相關性如圖8所示。

對比圖7、圖8可以看出，其LFM信號在時域上接收端存在較大的幅度變化(主要由于多普勒效應及多途疊加造成)，以至于頻域上相關峰出現分叉，降低了測量精度。

圖8 LFM信號經過水聲信道后的信號波形、頻譜和相關函數Fig.8 Waveform, spectrum and correlation function of the LFM signal after passing through the underwater acoustic channel

裝載發射聲源的試驗船只以8~10 kn左右的速度，在100~2300 m的范圍內周期發射信標信號，接收端進行相應處理后獲得其遙測的誤碼率如圖9所示。圖9所示的誤碼率是指在實際動態試驗中，接收端不能正確解算、錯誤解算及未能接收到的數據，均認為是誤碼數據。也就是說這里的誤碼包含了水聲遙測過程中所有的錯誤信息，比如由于聲線彎曲在某些區域帶來的信噪比急速下降，聲信號的反相位疊加等特殊情況，因此，實際動態試驗獲得的誤碼率較高。

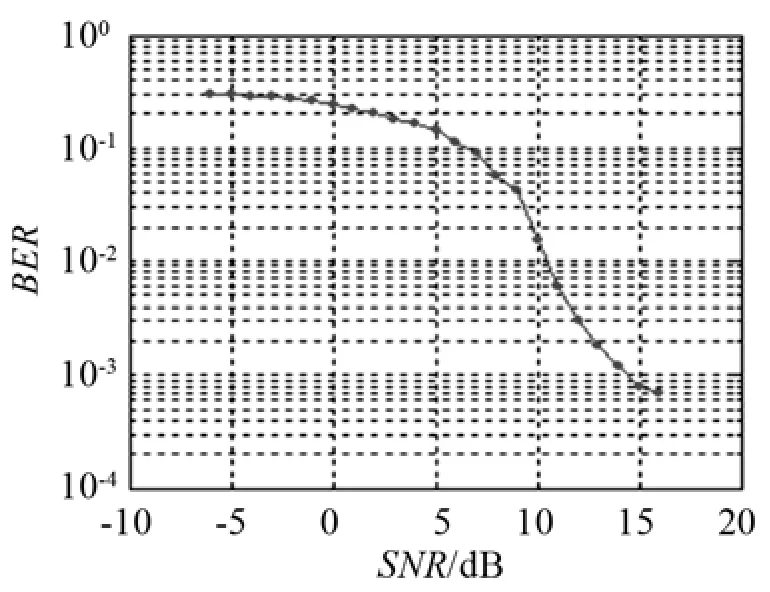
圖9 運動狀態下的實測誤碼率Fig.9 The measured bit error rate under the state of motion

由于水聲信道的多途效應影響，水聲信號與修正后樣本的相關峰會出現多個峰值，這里采用加窗及線性插值再次相關的方法[7]獲取精確時延值。

5 結 論

經過仿真及湖上試驗可以看出，HFM 信號與LFM信號相比，具有更高的多普勒容限，采用HFM信號與單頻信號相組合的方式，實現水下目標的航行參數遙測，可以有效校正多普勒頻偏的影響，遙測性能穩健，特別適用于水下高速、高機動目標的水聲遙測、水聲通信等。

參考文獻

[1] 田坦, 劉國枝, 孫大軍. 聲納技術[M]. 哈爾濱: 哈爾濱工程大學出版社, 2000.TIAN Tan, LIU Guozhi, SUN Dajun. Sonar technology[M]. Harbin: Harbin Engineering University press,2000.

[2] Busnel R G, Fish J F. Animal sonar system[M]. USA: Plenum Press, 1980.

[3] 楊長生, 杜金香, 馬艷. 一種寬帶仿生信號的小波變換域分析[J].聲學技術, 2007, 26(4): 105-109.YANG Changsheng, DU Jinxiang, MA Yan. Analysis of a wideband bionic signal in wavelet transform domain[J]. Technical Acoustics, 2007, 26(4): 105-109.

[4] 李志舜. 魚雷自導信號與信息處理[M]. 西安: 西北工業大學出版社, 2003, 10.LI Zhishun. Signal and information processing homing torpedo[M]. Xi’an: Northwestern Polytechnical University, 2003, 10.

[5] 惠俊英. 水下聲信道[M]. 北京: 國防工業出版社, 1991.HUI Junying. Underwater acoustic channel[M]. Beijing: National Defence Industry Press, 1991.

[6] 林偉. 遠程水聲通信技術的研究[D]. 西安: 西北工業大學碩士學位論文, 2005.LIN Wei. Study on long-range acoustic communication technology[D]. Xi’an: Master's degree thesis of Northwestern Polytechnical University, 2005.

[7] 劉松海, 冼觀福, 廖述常. 同步信標在水下機動小目標軌跡測量中的高精度時延估計方法[J]. 聲學技術, 2008, 27(26): 903-906.LIU Songhai, XIAN Guanfu, LIAO Shuchang. A method of high precision time delay estimation in underwater moving mini-tracking with synchronous beacon[J]. Technical Acoustics,2008, 27(26): 903-906.