聲吶導流罩內聲場特性研究

張洋波

(中國船舶重工集團公司第七一〇研究所，湖北宜昌 443003)

0 引 言

聲吶導流罩為封閉的結構，其內部聲場和罩體的結構形式、選材等密切相關，導流罩內部聲場特性關系到聲吶系統的正常工作。研究聲吶導流罩自噪聲，關鍵在于處理內外流體與結構耦合的振動與聲輻射問題。對于在流體介質中內部充液的封閉結構內的聲場特性，目前已經有一些研究。文獻[1]采用解析方法，利用經典彈性理論推導了平面波入射雙層彈性球殼的內部聲場的計算公式，計算了無限水介質中內部充水雙層球殼內部場點的插入損失；文獻[2]將聲類比邊界元技術應用于殼內外聲場耦合，提出了一種計算流體目標聲散射的耦合邊界元方法，并通過變形圓柱法的算例進行驗證；文獻[3]通過有限元法計算得到聲吶平臺區各部分結構在激勵下的均方振速，采用經驗公式求得輻射聲壓，最后合成聲吶平臺區自噪聲；文獻[4、5]采用有限元結合邊界元方法，對敷設聲學材料的聲吶平臺結構的振動和內部聲場進行計算和對比分析。

對于規則形狀的封閉結構，如薄球殼，可以通過解析的方法計算得到；對于復雜結構來說，解析方法難以求解，通常采用數值方法來計算。有限元法[6]可以求解這種問題，但是聲學處理功能弱，且只能采用有限邊界區域模擬外部無限水域，這樣的計算效率和精度都不高。邊界元法[7]降低了求解問題的空間維數，并且滿足無限遠流體全吸收邊界條件，可以同時求解內部和外部區域中的聲場。有限元結合邊界元法充分利用兩者的優勢，是處理結構振動和聲場的有效方法。

本文采用有限元法-邊界元法數值計算，并結合實驗的方法，研究機械激勵下聲吶導流罩內部聲場的分布特性，對導流罩的自噪聲中機械激勵噪聲作出預報。在此，機械激勵噪聲是指機械激勵下產生的結構振動傳遞至導流罩部位，引起的結構噪聲向導流罩內部輻射形成的。

1 理論基礎

1.1 聲場間接邊界元分析

對于具有任意封閉結構表面S的振動結構，振動結構為薄殼結構，在內外部均充滿了均勻、各向同性的理想介質。

在內外部區域中，當激勵源隨時間作簡諧變化時，有Helmholtz微分方程[8]此外，交界面上速度與聲壓滿足邊界條件，無窮遠處還滿足Sommerfeld輻射條件。

最終可得單頻聲場下的Helmholtz積分方程為

式中：E、I分別表示位置處于結構外部、結構內部；當r∈S時，p(r)前面的系數1/2僅適用于光滑結構表面。

間接邊界元法可以從直接邊界元法中推導出來，將直接邊界元法的Helmholtz積分方程分別應用在結構邊界表面的兩側，則可以得到：

式中，C1(r)、C2(r)分別為邊界面上內外場處的聲壓參與系數，且兩者滿足關系：

在內外場中定義的邊界面上的單位法向向量的方向是不同的，滿足如下關系：

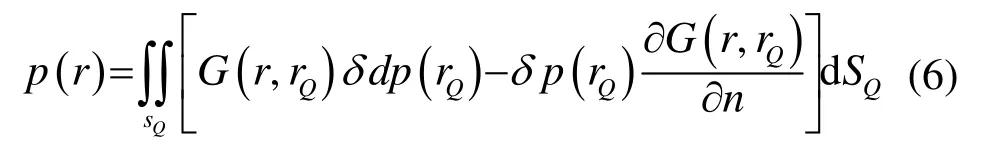
由上面三式可以得到如下表達式：其中δdp(rQ)、δp(rQ)分別表示邊界面兩側的法向壓力梯度差(單層勢)和壓力差(雙層勢)：

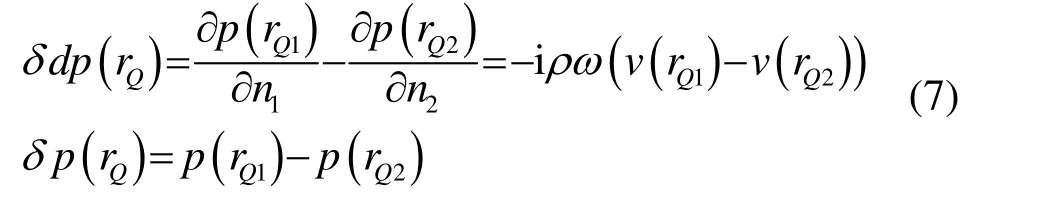
結構表面上任一點的基本變量可以用結構模型上節點的基本變量及其形函數表示。利用變分原理，假設Neumann邊界條件，在結構表面上進行離散，可得關于基本變量的間接邊界元求解方程：

其中：[A]是對稱矩陣；{Fa} 是激勵函數向量。

由式(8)得到結構邊界面上的基本勢函數變量，再利用式(6)可以計算整個聲場域中任一點聲壓。

1.2 間接邊界元流體模型與有限元結構模型的耦合

將結構振動的運動方程和聲場輻射的積分方程通過耦合系數矩陣聯系在一起，可以得到結構和聲耦合矩陣方程為：

其中：[K]是結構剛度矩陣；[M]是結構的質量矩陣；[C]是結構阻尼矩陣；{u}是結構位移；{x}是結構表面的未知基本變量；[CAD]和[CDA]是耦合矩陣；{Fd} 是結構機械載荷；{Fa} 是流體模型載荷。

2 導流罩內聲場數值與實驗研究

2.1 實驗條件及計算模型

導流罩分為底板(包括矩形板、縱橫肋)和上蓋(1/4球殼、1/4橢球殼、縱橫肋和連接裙帶)兩部分，中間通過密集的螺栓連接，寬度方向對稱，底板長為3.1 m，寬為1.46 m，如圖1所示。

在底板三個基座位置分別安裝三個激振器，激勵方向垂直于底板面，自球狀艏部的激勵開始依次定義工況1、工況2、工況3這三種激勵工況。在實驗中采用的激振器是一種大功率激振器，這種激勵源可滿足信噪比要求，但同時其輸出力并不穩定。為避免由此帶來的問題，在后面還需要對結果作一定處理。

導流罩全部采用鋼材料(包括底板)，其楊氏模量 為 2 .1× 1011N/m2， 泊 松 比 為 0.3， 密 度 為7800 k g/ m3。

圖1 導流罩實物圖Fig.1 Actual sonar dome

實驗在某湖實驗站開展，湖面開闊，水深在40m左右，夜晚背景噪聲較低。導流罩模型內部充滿水，置于開闊的水域中。

在計算導流罩模型之前，經過球殼模型內聲場的計算已驗證了Sysnoise軟件中FEM+IBEM方法的準確性，下面采用此方法對導流罩進行計算。

在ANSYS中，對導流罩模型進行建模，數值計算模型是根據實驗中實際的導流罩模型建立的，計算模型和實驗采用模型一致，如圖2所示，這里將螺栓連接視為固定連接。

圖2 導流罩模型圖Fig.2 Sonar dome model

根據實驗采用的工況對數值計算模型施加激勵，激勵的位置和方向一致，如圖3所示。數值計算中施加的是單位力，這與實驗中的情況不同。

在導流罩內部均勻布放 32只水聽器測量內部空間的聲壓，因為艏部空間較大，布置上下兩層水聽器，如圖4所示，圖中白點位置代表一只水聽器，而黑點位置代表此處的垂直底板面布置了上下兩只水聽器。在導流罩底板上布置6個加速度計用于測量結構的振動量，如圖3所示。

從32只水聽器測得的聲壓中選取艏部、尾部、中間三個位置的聲壓作為代表，即圖4中a、b、c三點的聲壓，其中a點取上層水聽器測得的聲壓。對測得的結果作1/3倍頻程處理，并計算均方值。表1列出工況1激勵下在100~2000 Hz之間測得的聲壓和均方聲壓。

圖3 激勵源和加速度計的位置Fig.3 Positions of excitation sources and accelerometers

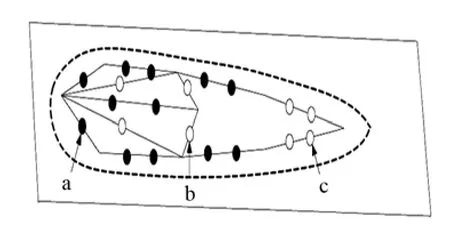
圖4 水聽器的布放位置Fig.4 Positions of hydrophones

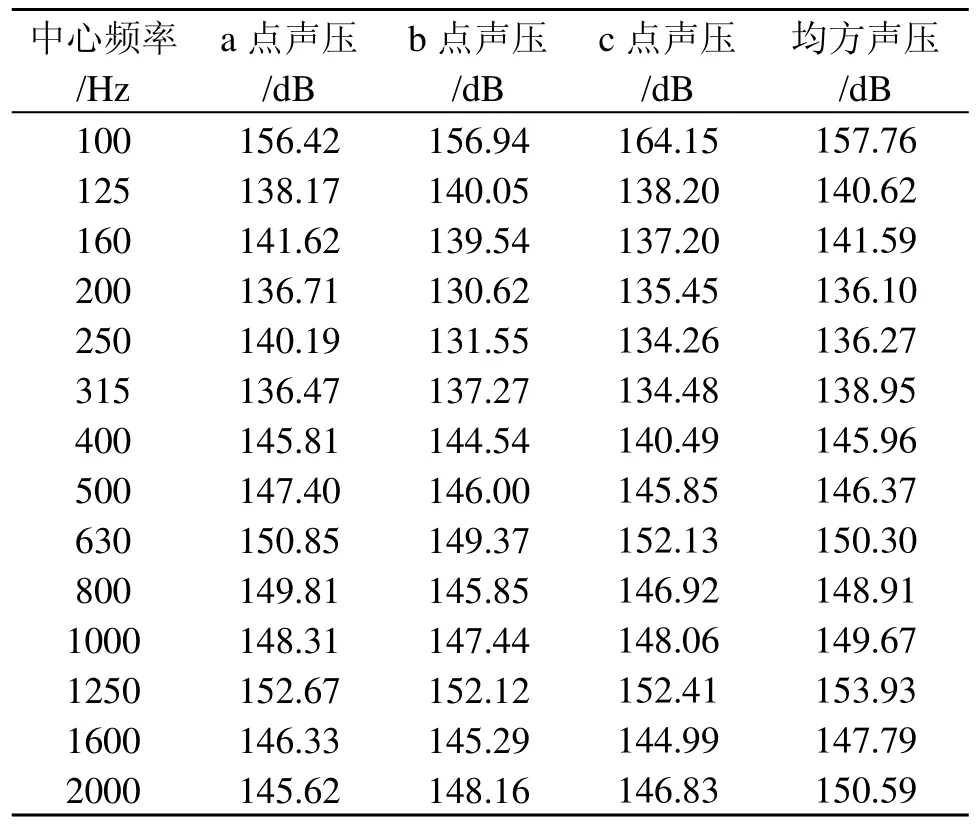
表1 工況1測得的聲壓Table 1 Sound pressures under the first condition

2.2 內聲場數值計算結果

導流罩模型分別加載三種不同的工況，激勵力大小為1 N，計算100~2000 Hz之間的1/3倍頻程頻率，對導流罩內部全空間各點聲壓作均方處理，比較內部聲場均方聲壓隨頻率的變化規律，如圖5所示。

圖5 不同工況下均方聲壓頻譜圖Fig.5 Frequency spectrums of mean square pressures under different conditions

比較圖5中不同工況下的均方聲壓結果，可以看出，內部空間均方聲壓隨著頻率的增大在起伏中逐漸增大，工況1、工況2的聲壓變化趨勢比較一致，量值也比較接近；工況3在大部分頻段內導流罩內聲場聲壓響應比較小，這可能是由于激勵位置靠近上蓋與底板的連接裙帶，此位置剛度較大，難以激起響應。

2.3 數值與實驗結果對比分析

在采用數值法對封閉結構的內外部聲場仿真過程中，可以設置任意的激勵大小和方向，而且僅對單一頻率進行分析。由于實驗中激振器的輸出力不穩定，導致不能直接比較數值計算所得聲壓與實驗測得結果。在機械激勵下，結構本身會有振動量的產生，通常認為在理想流體中的封閉薄殼結構的振動和聲輻射是線性系統[9]，那么聲壓量與振動量之間也滿足線性關系。因此，考察結果可以采用聲壓振速比這種形式。

結構內部聲場是本文的主要研究對象，而空間均方聲壓可以描述整個聲場的特性，這里采用殼內聲場全空間均方聲壓值與底板所有點均方振速之比(pvr)的形式作為考察結果：

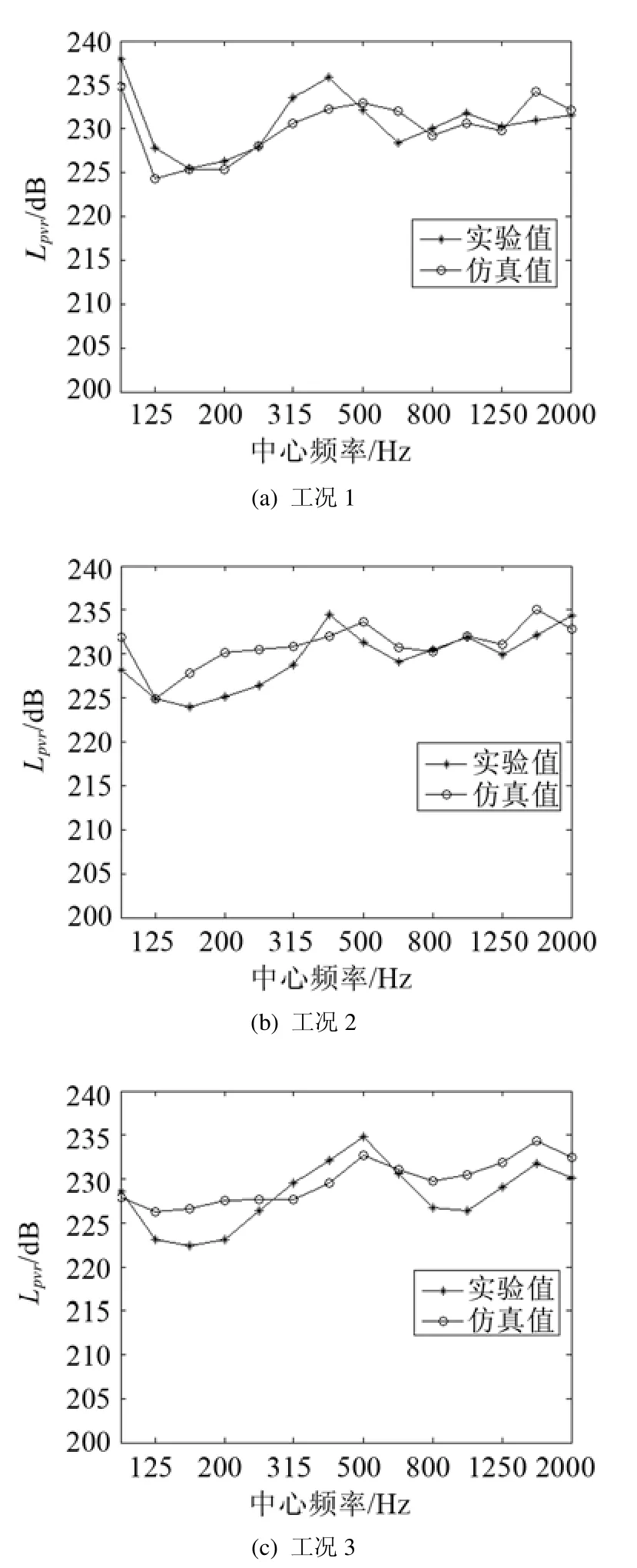
圖6 實驗與仿真的聲壓振速比曲線對比Fig.6 Comparison between experimental and simulation graph of the ratio of acoustic pressure and velocity

比較數值計算結果與實驗測量結果，如圖6所示，其中縱坐標為聲壓振速比pvr，可以看出，工況1與工況2兩者的聲壓振速比曲線的變化趨勢比較一致，這與兩種工況內部空間均方聲壓的比較結果類似。三種工況下，實驗測量結果與數值仿真結果比較一致，單頻下的聲級誤差基本不超過5 dB，由于結果以聲壓振速比形式呈現，數值上較大。

數值仿真與實驗測量的1/3倍頻程各頻段結果比較一致，反映出 FEM+IBEM 方法具有一定的實用性，同時也說明采用聲壓振速比這種結果形式表示封閉結構的聲場特性是可行的。

3 結 論

本文采用有限元法-邊界元法和實驗方法來分析封閉結構的內聲場特性，得出以下主要結論：

(1) 采用內部空間多點的聲壓均方值來表示封閉結構的聲場特性，實驗結果與仿真結果比較一致，這對以后的實驗有一定指導意義。

(2) 對于不同大小的機械激勵，可采用聲場均方聲壓與結構均方振速之比來對數值計算和實測結果進行對比驗證，聲壓-結構振速比可反映特定結構內的聲場特性，本文初步揭示了它的應用價值。

參考文獻

[1] 程釗, 陶猛, 范軍. 平面波入射球型導流罩的內部聲場分析[C]//第十二屆船舶水下噪聲學術討論會論文集, 2009: 220-225.CHENG Zhao, TAO Meng, FAN Jun. Analysis on inner sound field of spherical sonar dome under plane wave incidence[C]// The twelfth marine underwater noise Academic Symposium, 2009:220-225.

[2] 楊志剛, 王同慶. 邊界元計算內外聲場耦合及流體目標聲散射[J].哈爾濱工程大學學報, 2007, 28(2): 161-164.YANG Zhigang, WANG Tongqing. Coupling of exterior/interior field with BEM and numerical simulation of acoustic scattering of fluid target[J]. Journal of Harbin Engineering University, 2007,28(2): 161-164.

[3] 郭華林, 駱東平, 陳美霞, 等. 潛艇首部聲吶平臺區低頻自噪聲預報方法[J]. 艦船科學技術, 2005, 27(4): 74-77.GUO Hualin, LUO Dongping, CHEN Meixia, et al. Prediction method for low frequency of self-noise in submarine’s fore-body sonar platform area[J]. Ship Science and Technology, 2005, 27(4):74-77.

[4] 陳浩. 敷設聲學材料的聲吶平臺結構振動聲輻射計算分析[J]. 聲學與電子工程, 2010(4): 8-12.CHEN Hao. Analysis on structural vibration and acoustic radiation of sonar platform laying acoustic material[J]. Acoustics and Electronics Engineering, 2010(4): 8-12.

[5] 王紀會, 劉雨東, 劉彥森. 半球形聲吶導流罩空腔內部聲場分析[J]. 機械工程與自動化, 2010(3): 71-72, 75.WANG Jihui, LIU Yudong, LIU Yansen. Analysis of sound field in the sonar dome of hemispherical shape[J]. Mechanical Engineering Automation, 2010(3): 71-72, 75.

[6] Kallivokas L F, Bielak J. Time-domain analysis of transient structural acoustics problems based on the finite method and a novel absorbing boundary element[J]. J. Acoust. Soc. Am., 1993, 94(6):3480-3492.

[7] 徐張明, 沈榮瀛, 華宏星. 利用FEM/IBEM計算流體介質中的殼體的結構聲耦合問題[J]. 振動工程學報, 2002, 15(3): 363-367.XU Zhangming, SHEN Rongying, HUA Hongxing. Structural-acoustic coupling problem of an immersed shell by FEM/IBEM[J]. Journal of Vibration Engineering, 2002, 15(3):363-367.

[8] 何祚鏞. 結構振動與聲輻射[M]. 哈爾濱: 哈爾濱工程大學, 2001.HE Zuoyong. Structural vibration and acoustic radiation[M]. Harbin: Harbin Engineering University, 2001.

[9] 陳明, 王斌, 曹為午. 水下復雜殼體結構在多源激勵下的振動及聲輻射特性研究[J]. 聲學學報, 2009, 34(6): 498-505.CHEN Ming, WANG Bin, CAO Weiwu. Research on vibration and acoustic radiation of the submerged complicated shell structure with multiple excitations[J]. Acta Acustica, 2009, 34(6):498-505.