非線性參量B/A超聲成像的仿真與仿體實驗研究

蔡 雪，余錦華，汪源源，馬友能

(復旦大學電子工程系，上海 200433)

0 引 言

超聲成像經歷半個多世紀的發(fā)展，已廣泛應用于臨床診斷。早在 1980年 Muir和 Carstensen就提出聲波在生物組織中的傳播過程存在不可忽視的非線性現象，Starritt等更于1985年通過醫(yī)學儀器觀察到超聲波在肌肉中的非線性傳播[1]。單一頻率的發(fā)射波在組織中傳播時，隨著傳播深度的變化，其傳播速度在變化。由于波峰的聲速大于波谷的聲速，所以波形會發(fā)生畸變，產生與初始頻率成倍頻關系的頻率分量，這些新增的頻率分量叫做“諧波頻率”分量[2]。在聲波繼續(xù)傳播的過程中，將產生無限多的諧波。最后，發(fā)射的正弦波變?yōu)殇忼X波。諧波產生和累積的過程就是聲波傳播的非線性效應。

如果聲的傳播過程是等熵的，則介質的物態(tài)方程可以表示成泰勒級數的形式：其中：P為聲壓；ρ為密度；P0、ρ0分別為介質的靜態(tài)壓強和靜態(tài)密度。將線性項系數A、二次項系數B定義為A=(ρ?P/?ρ)0，B= (ρ2?2P/?ρ2)0，那么B和A的比值就是非線性參量B/A。它是超聲波在介質傳播過程中非線性效應大小的度量。與聲速、聲阻抗、聲衰減等線性參量相比，非線性參量更能反映生物組織的結構特征以及病變狀態(tài)的動態(tài)特性。作為超聲醫(yī)學診斷中的一個新參量，B/A近年來在超聲醫(yī)學診斷與生物聲學中出現了可喜的應用前景。

非線性參量B/A的測量方法主要分為兩大類，一類是熱力學方法，另一類是有限振幅聲波法[3]。雖然熱力學方法測量樣品的非線性參量B/A具有一定的精度，但是要求有加壓裝置，所以不適用于臨床。與之相反，有限振幅聲波法由于實驗操作簡單，成為了研究熱點。迄今為止，研究者提出了不少基于單頻發(fā)射波或多頻發(fā)射波的有限振幅聲波法。這些方法結合傳統的圖像重建方法，形成了不同的B/A成像技術。

Nakagawa等[4]于1986年提出基于參量陣和二次諧波的非線性成像方法。基于參量陣的非線性成像方法是根據參量陣理論，即兩列不同頻率初始波在介質中傳播方向相同時，會產生差頻波，且這一差頻波是非線性參量沿聲波傳播路徑的線積分。該方法在獲取差頻波幅值后利用傳統的 CT成像算法重建出非線性聲參量的層析圖像。基于二次諧波的非線性成像方法以 Burges非線性傳播方程為基礎，即聲波在介質中傳播所產生的二次諧波可以看作是非線性聲參量沿傳播路徑的線積分。通過測量聲波在傳播距離上產生的二次諧波幅值，以其為投影數據，利用傳統的CT成像算法重建出非線性聲參量的層析圖像。

Fujii和 Akiyama等[7]提出了另一種測量B/A參量的方法。該方法連續(xù)發(fā)射頻率分別為f0和2f0的發(fā)射信號，從發(fā)射頻率為f0的接收信號中提取諧波幅值，在發(fā)射信號為2f0的接收信號中提取基波幅值，將得到的諧波幅值和基波幅值的平方相比便可得到非線性參量B/A的值。此外，龔秀芬等[6]運用該方法得到了等深度脈沖回波 C掃描B/A成像。

2011年，Varray等[8,9]考慮介質中非線性參量的非均勻分布的情況，提出了直接法(Direct Method, DM)與比較法(Comparative Method, CM)的拓展形式：擴展直接法(Extended Direct Method,EDM)和擴展比較法(Extended Comparative Method,ECM)，以提高B/A測量的精度。此外，他們通過濾波從 B型諧波圖像中濾除斑點噪聲，得到與二階聲場相關的圖，在圖上選定參考介質區(qū)和待測介質區(qū)，運用ECM即可得到B/A參量成像圖。

B/A參量成像結果與B/A測量技術有直接關系,而上述B/A參量成像所用到的有限振幅聲波法可分為兩種：直接法和比較法。直接法指向組織發(fā)射一定頻率的有限振幅超聲波，從接收信號中提取所需信號幅值，計算其與發(fā)射信號幅值平方的比來得到組織B/A值。Chavrier[10]和 Wallace[11]進行不同實驗驗證了傳統的直接法測量均一組織的B/A參量誤差在 5%以內，而 Varray等[8,9]在此基礎上提出了適用于B/A分布不均的擴展直接法(EDM)。Fujii和 Akiyama等[7]提出的方法也可以歸于直接法，只是這一方法用2f0發(fā)射源的接收信號的基波幅值代替f0發(fā)射源的幅值。比較法則主要測量聲波在兩種不同介質中傳播時二次諧波的變化。其中一種介質的B/A值是已知的，被稱為參考介質。同樣為了使比較法適用于B/A參量分布不均的組織，Varray等[8,9]提出了擴展比較法(ECM)。

本文通過仿真與仿體實驗比較有限振幅聲波法測量非線性參量B/A的幾種經典方法。仿真和仿體實驗結果均表明：擴展的比較法(ECM)測量準確性高，運用該方法結合濾波反投影仿真實現B/A參量層析成像，成像結果能很好地描述簡單組織中的B/A參量分布。

1 測量非線性參量的有限振幅聲波法

1.1 直接法(DM法)

超聲在組織中傳播時，產生的二次諧波p2與組織的非線性系數β的關系為：

其中：ρ0和c0分別表示組織的密度和聲速；x為聲波傳播的距離，f為發(fā)射源的頻率，p0為發(fā)射源的振幅。由式(2)可知，發(fā)射一定頻率的有限振幅波，當其在組織中傳播一定距離后，從接收到的信號中提取出二次諧波幅值，便可得到組織的非線性系數。

為了使測量結果更加準確，在計算時需要補償聲波在組織中傳播的衰減。此外，還需要測量不同傳播距離下產生的二次諧波幅值，繪制p2(x)/xp02對x的曲線，并在該曲線上進行線性外推，得到x→0時p2(x) /xp02的值。計算β值時只需將此值代入：

2.1 出生后24 h細胞因子比較 從生后24 h臨床監(jiān)測動態(tài)指標來看，非BPD早產兒入院前外周血清IL-1β、IL-6、IL-8等細胞因子水平比BPD早產兒的整體水平要高，差異有統計學意義（P＜0.05），見表1。

其中，α1和α2分別對應基波和諧波的衰減系數。

1.2 擴展的直接法(EDM法)

傳統的直接法是在假設組織的非線性系數是均一的前提下進行的。對于β非均勻分布的情況，式(3)只能得到整個組織的平均值。為了準確測得非均勻組織中非線性系數的值，Varray等[8,9]將傳統的直接法進行了擴展，認為組織的非線性系數不再是常數，不同傳播距離上的非線性系數是不同的，于是有：

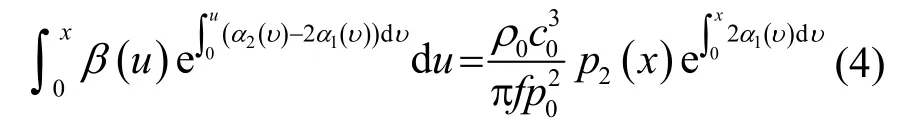
對式(4)左右兩邊均作求導運算，則可以得到非線性系數分布不均時的計算表達式：

1.3 Akiyama和Fujii方法

Akiyama和 Fujii[7]利用超聲回波信號測量組織的B/A值。發(fā)射頻率為f0的正弦波并從接收信號中提取出超聲波在組織中傳播所積累的二次諧波幅值。隨后發(fā)射頻率為2f0的正弦波，從接收信號中提取其基波幅值。于是非線性系數的計算式為

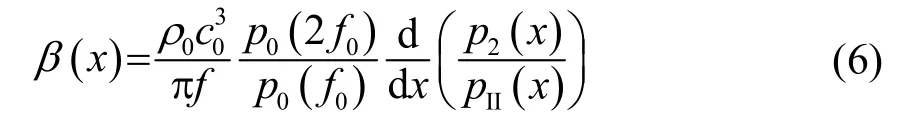
其中：p0(f0)和p0(2f0)分別為兩次發(fā)射波的初始振幅；p2(x)是頻率為f0的發(fā)射波產生的二次諧波幅值；pII(x)是頻率為 2f0的發(fā)射波經過組織后接收到的基波幅值。雖然該方法主要針對回波信號提出，但對于透射波同樣適用。

1.4 比較法(CM法)

比較法是插入取代法的特殊形式，最初是由龔秀芬等提出[5]，其核心思想是：在選定B/A參量已知的參考介質后，測量同一頻率的發(fā)射源在參考介質和待測介質中傳播積累的諧波幅值，從而得到待測介質的B/A值。如果參考介質和待測介質的長度d相等，兩種介質的聲速和密度都已知，同時考慮衰減和衍射的影響對該方法進行改善，那么，待測介質的非線性系數可以表示為

其中：下標為 0和下標為i的參量β、ρ和c分別對應參考介質和待測介質的物理量；p2i和p20分別表示待測介質和參考介質的二次聲壓幅值；I1和I2是衰減相關項，I1=exp(?α1d)，I2=exp(?α2d/2)，其中α1和α2分別表示基波和諧波的衰減系數；D'和D''是兩個無量綱項，表示透射系數，其表達式為：

1.5 擴展的比較法(ECM法)

Varray等[8,9]指出，如式(7)所示的比較法更適用于均勻介質。為了使得比較法在非均勻介質中也同樣適用，他們對原先的比較法進行了擴展。在擴展的比較法(ECM)中，依然選取非線性參量均勻分布的介質作為參考介質，那么其二次諧波幅值(p20)為

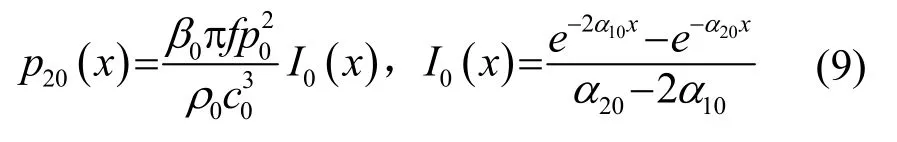
由于待測介質的非線性參量和衰減系數都是非均勻分布的，可以用章東等提出的表達形式[12]來表示其二次諧波幅值(p2i)：

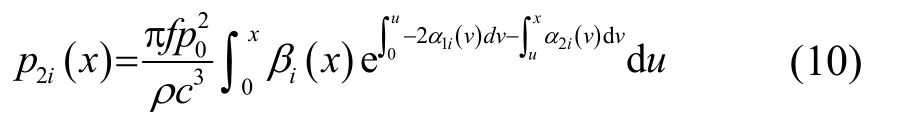
在式(9)、式(10)中，下標為 0和i的參量分別對應參考介質和待測介質的物理量。以二次諧波幅值的表達式為基礎，可以得到非均勻待測介質的非線性系數：

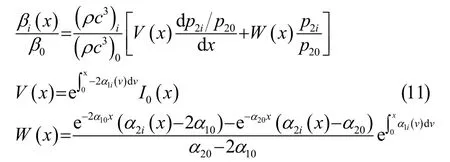
其中，V和W是與參考介質和待測介質的衰減系數相關的兩個系數。

2 非線性參量測量實驗與結果

2.1 仿真實驗與結果

目前，已有幾種模型來模擬聲波在非均勻介質里的非線性傳播過程。Pinton等[13]于 2009年提出了非線性衰減的全波(Full-wave)模型，并運用時域有限差分法(Finite Difference Time Domain,FDTD)得到了其數值解。與目前應用最為廣泛的KZK拋物線方程相比，Full-wave模型不受近軸假設的限制，其對遠場超聲波束的描述更為準確。Full-wave模型的數學形式為

其中：p表示聲壓；c0為聲速；ρ0表示靜態(tài)密度；δ為擴散系數；β(β=1+B/ 2A)是非線性系數。式(12)左邊前兩項表示波動方程的線性項，第三項表示超聲的熱耗散，第四項為非線性項，其余兩項為密度變化和弛豫衰減項。

本文在模擬超聲在組織中的非線性傳播時，采用 FDTD求解該模型[13]。將聲波傳播區(qū)域劃分為若干個小的網格點，每個網格點的大小為 0.1 mm×0.1 mm，所以空間步長Δx為 0.1 mm。Fullwave模型中的各偏微分項近似為差分項后，計算每一個時間步(時間步長 Δt= Δx/c0/2)上的聲場，并通過數值迭代對聲場進行更新。此外，為了將仿真區(qū)域局限在有限空間，在截斷邊界設置完全匹配層(Perfectly Matched Layer, PML)[14]。

按照組織的非線性參量分布均勻與否，我們進行了兩組仿真實驗。一組是建立三種均勻的生物組織(腎、肝和肌肉)的仿真模型。由于比較法和擴展比較法都需要選定參考介質，因此我們也建立了水的仿真模型。四種組織的聲學參數的設定與相關文獻的值是一致的，其中水、肝、腎和肌肉的B/A參量分別設為5.2、6.8、7.2和7.5。另一組模型的組織非線性參量是變化的，具體為

仿真中設置的探頭為 65個陣元的線陣探頭，陣元間隔為 2個網格點。當周期為 10、振幅為 1 MPa、頻率為1 MHz(或2 MHz)的高斯調制正弦脈沖波在組織中傳播時，每隔5 mm接收一組數據。聲波在組織中傳播10 cm后停止接收。對接收到的信號進行傅里葉變換。為了提取接收信號中二次諧波量(或基波)，將其送入一個中心頻率為 1 MHz(或 2 MHz)、帶寬為 0.6 MHz的四階巴特沃茲帶通濾波器進行濾波。

對于第一組組織模型，五種方法測得的組織非線性參量B/A的平均值如表1所示。第二組組織模型測量結果如圖1所示。

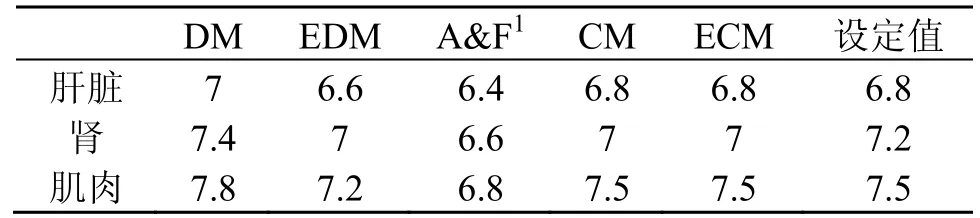
表1 均一組織B/A測量仿真結果Table 1 Simulation results of B/A measurements for homogeneous tissues

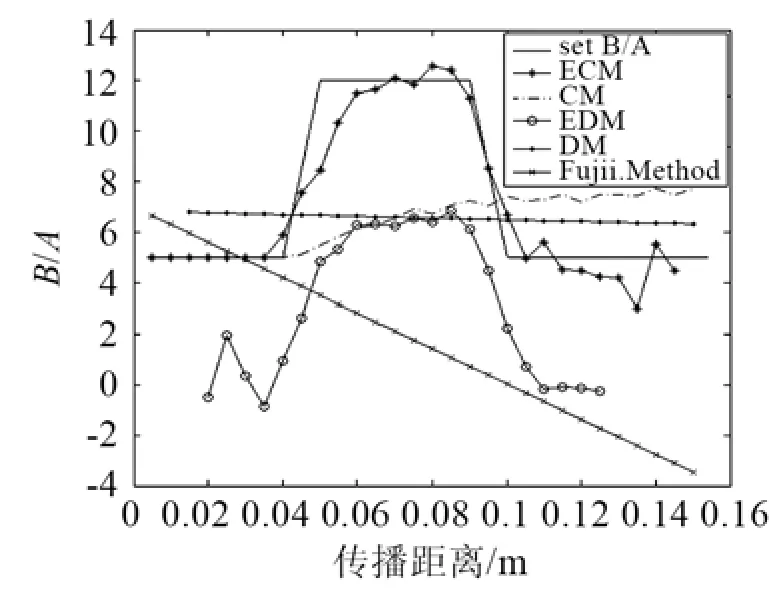
圖1 非均勻組織的B/A測量仿真結果Fig.1 Simulation results of a set of inhomogeneous B/A setting measurements for inhomogeneous tissues

從結果可知：對于均勻組織，DM、EDM、CM、ECM的測量結果都很理想。Akiyama和Fujii方法結果稍差，但是誤差也在 10% 以內。然而對于非線性參量分布不均的情況，Akiyama和 Fujii方法隨傳播深度的增加，結果越加偏離正確值，無法很好描述組織非線性參數的變化。此外，傳統的 DM也無法反映組織的非線性參量變化，只能得到整個組織B/A的平均值。盡管 CM在組織參量沒發(fā)生變化時測量值與設定值幾乎一致，但是當組織B/A發(fā)生變化后，該方法不再有效。EDM盡管能很好地識別組織B/A的變化趨勢，但是其測量值偏離設定很多。而 ECM不僅能識別組織非線性參量的變化，而且其測量值也很接近設定值，只在后端有一定振蕩。

由仿真實驗可以得到結論：ECM是五種方法中最有效的測量法。

2.2 仿體實驗與結果

仿體實驗的操作平臺是基于非線性超聲設備Ritec RAM-5000搭建的。該系統擁有高能量脈沖輸出端和相敏超外差接收器。可使聲學介質的非線性研究更加簡單和精確。實驗框圖如圖2所示。

運用 Ritec RAM-5000系統脈沖信號輸出端經50 ?的負載電阻與發(fā)射探頭連接，接收端探頭經前置放大器后進入 Ritec RAM-5000系統輸入端，該信號再由系統信號顯示端輸入至示波器顯示。實驗中選用的兩個平面水浸探頭分別為泛美V302-SU和 V304-SU，中心頻率分別為 1 MHz和 2.25 MHz。

圖2 實驗裝置圖Fig.2 Experimental layout

仿體實驗主要是針對健康的豬肉組織進行的，將三種組織都分為不同厚度的小樣以便得到不同傳播距離下的接收信號。與仿真實驗一樣，為了實現 CM和 ECM，假設水為參考介質。表2是測量中用到的組織的線性聲學參量匯總。表3為不同方法對三種組織的測量結果。

表2 組織的線性聲學參量Table 2 Linear acoustical parameters of tissues

表3 仿體實驗B/A測量結果Table 3 Phantom experiment results for B/A measurement

由于每種組織的非線性參量都是分開測量的，每種組織都可看作是均勻組織。由于EDM和ECM可測得不同傳播距離下組織的B/A值。為了避免近場區(qū)域多重反射引起的干擾(實驗發(fā)現測量距離大于1.8cm時干擾減小)，將仿體切割為15個不同厚度{d|d=2cm: 0.3cm: 6.5cm}的小樣。表3中EDM和ECM測量值是不同距離下測得值的平均。

從測量結果可得，雖然幾種方法測得組織的非線性參量B/A值的誤差(DM：8%，EDM：5%，A&F：6%，CM：4%，ECM：2%)都在誤差允許范圍內，而 DM和 CM對應的拓展方法都比這兩種方法得到的測量結果要好，但 ECM測量得到的值與相關文獻給出的值最接近。

3 基于ECM的B/A成像計算機仿真

3.1 基于ECM的B/A層析成像

由以上仿真和仿體實驗，可以看出ECM能較好描述組織B/A的變化。而式(9)和式(10)之比可以表示為

將式(14)中的積分因子看成一個整體，整理可得：

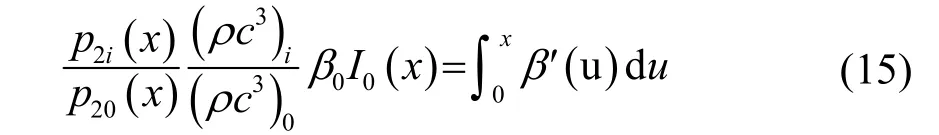
其中式(15)左邊可看作是β'(u)沿聲傳播路徑x的線積分。如果在某一角度上等間距求得待測介質和參考介質的二次諧波聲壓之比，就可以利用CT的重建算法來進行非線性參量的層析成像[15]。

設投影數據p(u,θ)為

按圖3的 CT掃描系統所示，在 0°～180°間等角度地旋轉組織，并在每一角度下等間隔收集投影數據，掃描完成得到投影矩陣后便可通過濾波反投影算法得到β'(u)。

重建β'(u)的關鍵在于斜坡濾波器|w|的選擇，本文選用 Sheep-Logan濾波器在頻域對投影矩陣進行濾波，其頻響曲線為

圖3 CT掃描系統Fig.3 CT scanning system

其中d為等間隔掃描的間隔。對濾波后的投影數據在時域進行線性內插，得到β'(u)后對其進行衰減補償便可得到B/A的層析成像。

3.2 成像實驗及結果

對圖4(a)和圖5(a)所示的組織模型(4×4 cm2，即 400×400網格點)進行層析成像。圖4(a)所示組織模型，中心為一個圓形非線性系數β為7的脂肪類組織，外層為水，非線性系數β為 3.5。圖5(a)所示組織模型為了增加組織模型的復雜度，在圖4(a)所示組織模型的中心圓內又增加了一個小圓，其非線性系數β為 4.8。按圖3所示的掃描方式，發(fā)射探頭和接收探頭之間的距離不變，待測樣品每旋轉 5°時，發(fā)射探頭和接收探頭同時沿u軸，中心陣元每隔 10個網格點移動一次進行掃描，仿真所用的探頭陣元數為 65。為了減少探頭陣元之間的相互干擾對成像結果的影響，每個采樣步長上只取中心陣元得到的數據作為采樣數據，并從采樣數據中提取出二次諧波幅值。采樣組織的整個掃描過程可得到不同投影區(qū)域積累的二次諧波幅值(41×37的矩陣)。選定圖4(a)和圖5(a)中兩線之間的區(qū)域為參考介質，則將得到的二次諧波幅值矩陣除以參考區(qū)域的二次幅值，并乘以參考區(qū)域的非線性系數與其余線性參數之比便可得到投影矩陣(41×37)。對投影數據進行濾波反投影重建后，便可得到該組織的B/A層析圖像，結果如圖4(b)和圖5(b)所示。提取其中心一條線，可得到非線性參量的一維分布，如圖4(c)和圖5(c)所示。

圖4 組織模型I的 B/A層析成像結果Fig.4 B/A tomography results for tissue model I

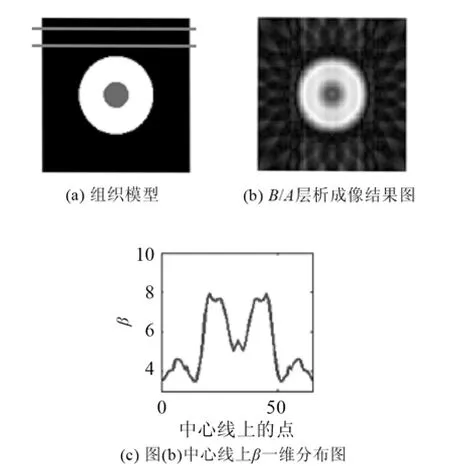
圖5 組織模型II的B/A層析成像結果Fig.5 B/A tomography results for tissue mode II

從成像結果可以看出，基于 ECM的非線性成像結果與組織模型較吻合，能夠很好地反應組織的非線性參量分布。

4 總結與展望

為了獲得較好的B/A成像結果，本文比較了生物組織非線性B/A參量測量的幾種經典算法，希望從中選擇最優(yōu)的方法進行成像。仿真和仿體實驗均表明：ECM 法不但測量精確，而且其測量結果能很好地反映組織中B/A的變化。運用 ECM進行B/A成像的仿真模擬，結合ECM與濾波反投影得到的B/A層析成像結果與設定的組織模型吻合程度較高。

在本文的仿真和仿體實驗中，忽略了組織中散射點對結果的影響。而在實際中，散射點對超聲波在組織中傳播是有影響的，以后對于B/A成像的研究也應考慮散射點的影響。

參考文獻

[1] 余錦華, 汪源源. 醫(yī)學超聲成像的模擬研究[J]. 聲學技術, 2011,30(1): 33-40.YU Jinghua, WANG Yuanuan. Simulation study of medical ultrasound imaging[J]. Technical Acoustics, 2011, 30(1): 33-40.

[2] Choudhry S, Gorman M, Charboneau W, et al. Comparison of tissue harmonic imaging with conventional US in abdominal disease[J]. Radiographics, 2000, 20(4): 1127-1135.

[3] Bj?rn? L. Forty years of nonlinear ultrasound[J]. Ultrasonics,2002, 40(1-8): 11-17.

[4] Nakagawa Y, Nakagawa M, Yoneyama M, et al. Nonlinear parameter imaging computed tomography by parametric acoustic array[C]// Proceeding of IEEE International Ultrasonics Symposium(IUS), 1984: 673-676.

[5] Gong X, Feng R, Zhu C, et al. Ultrasonic investigation of the nonlinearity parameter B/A in biological media[J]. J. Acoust. Soc.Am., 1984, 76(3): 949-950.

[6] Gong X, Zhang D, Liu J, et al. Study of acoustic nonlinearity parameter imaging methods in reflection mode for biological tissues[J]. J. Acoust. Soc. Am., 2004, 116(3): 1819-1825.

[7] Fujii Y, Taniguchi N, Akiyama I. A new system for in vivo assessment of the degree of nonlinear generation using the second harmonic component in echo signals[J]. Ultrasound Med. Biol., 2004,30(11): 1511-1516.

[8] Varray F, Pasovic M, Cachard C, et al. Acoustic nonlinearity parameter of tissue on echo mode: review and evaluation of the different approaches for B/A imaging[C]// Proceeding of IEEE International Ultrasonics Symposium (IUS), 2009: 41-44.

[9] Varray F, Basset O, Tortoli P, et al. Extensions of nonlinear B/A parameter imaging methods for echo mode[J]. IEEE Trans. Ultrasonics. Ferr., Freq. Control, 2011, 58(6): 1232-1244.

[10] Chavrier F, Lafon C, Birer A, et al. Determination of the nonlinear parameter by propagating and modeling finite amplitude plane waves[J]. J. Acoust. Soc. Am., 2006, 119(5): 2639-2644.

[11] Wallace K, Lloyd C, Holland MR, et al. Finite amplitude measurements of the nonlinear parameter B/A for liquid mixtures spanning a range relevant to tissue harmonic mode[J]. Ultrasound Med. Biol., 2007, 33(4): 620–629.

[12] Zhang D, Gong X, Ye S. Acoustic nonlinearity parameter tomography for biological specimens via measurements of the second harmonics[J]. J. Acoust. Soc. Am., 1996, 99(4): 2397-2402.

[13] Pinton G, Dahl J, Rosenzweig S, Trahey G E. A heterogeneous nonlinear attenuating full-wave model of ultrasound[J]. IEEE Trans. Ultrasonics. Ferr. Freq. Control, 2009, 56(3): 474-488.

[14] Li X. PML condition for the numerical simulation of acoustic wave[C]// Proceeding of International Conference on Computing Control and Industrial Engineering, 2010: 129-132.

[15] Zhang D, Gong X. Experimental investigation of the acoustic nonlinearity parameter tomography for excised pathological biological issues[J]. Ultrasound Med. Biol., 1999, 25(4): 593-599.