探尋物理量間定量關系的方法——對數法

潘學升

（高淳高級中學，江蘇 南京 211300）

在探究物理規律時有時要具體探究物理量之間的定量關系，若物理量之間是線性關系或是反比關系只要先觀察實驗數據，后進行猜想和進行驗證即可，整個過程并不復雜，但要是遇到復雜的定量關系，例如是二次方或是三次方關系或更復雜的關系，若仍采用先猜想后驗證的方法，可能在尋找它們的規律時就會花費大量的時間，有時甚至無法找到所要的結果，很顯然先猜想后驗證的方法并不是最優的辦法.如能通過對數據的處理先大致找到物理量之間的定量關系，再進行猜想與驗證，這樣處理就方便得多，利用數學中的對數就可以做到這一點，這種方法稱之為對數法.下面就結合高中物理中遇到的較為復雜的定量關系來舉例說明.

1 對數法處理數據的基本原理

圖1

當兩個物理量不是成線性關系或反比關系時，我們可以根據條件先設一個函數，如y＝axb，a、b為常數，則lgy＝lga＋blgx，畫出lgy－lgx的圖像，如圖1所示，則根據圖像分析可知直線的斜率為b，截距為lga，其中a和b就是我們所要尋找的數值.

2 對數法在探究物理規律時的應用

2.1 對數法在探究單擺周期與擺長的定量關系的應用

表1是某學生在探究影響單擺周期與擺長關系時得到的數據，如表1所示，請根據數據找到T與L的定量關系.（注：數據來源于文獻［1］）

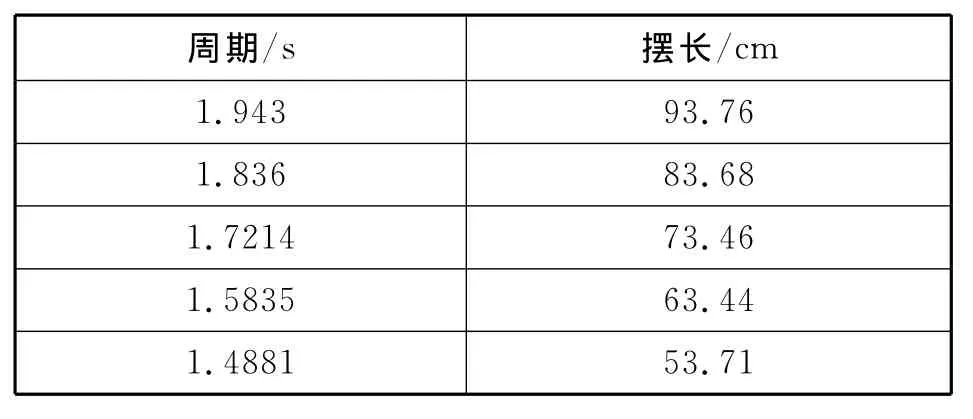
表1

分析：為便于處理，先把周期放大10倍，擺長放大100倍，然后取對數，得到表2.（注：在處理過程中不會影響log2T－log2L關系中的log2L前的系數，對數中是以2為底）

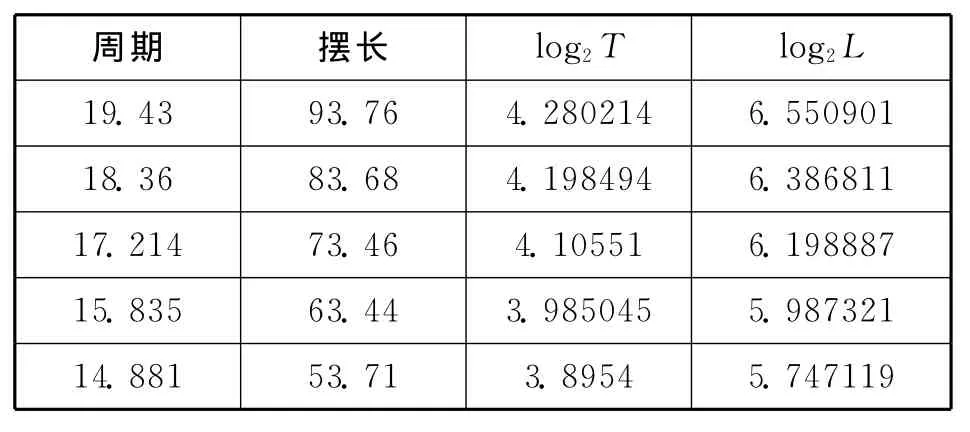
表2

畫出log2T－log2L的關系圖，如圖2所示，從圖像中可以得到斜率為0.4884，這與0.5非常接近，可猜測那么我們只要做出T2－L的圖像，觀察圖像是否為過原點的一條直線，如果是就證明猜想正確.

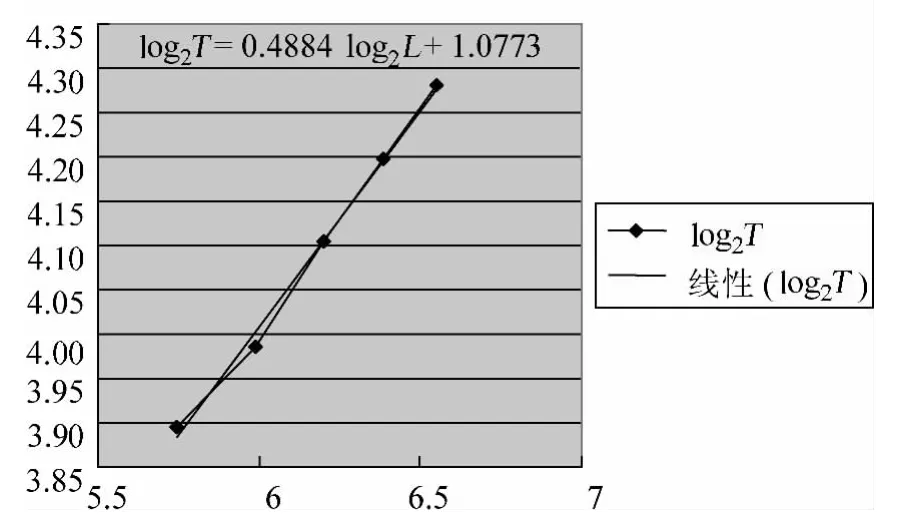
圖2

先對表2數據進行處理，得到表3.根據表中數據繪制出T2－L的圖像，如圖3所示.

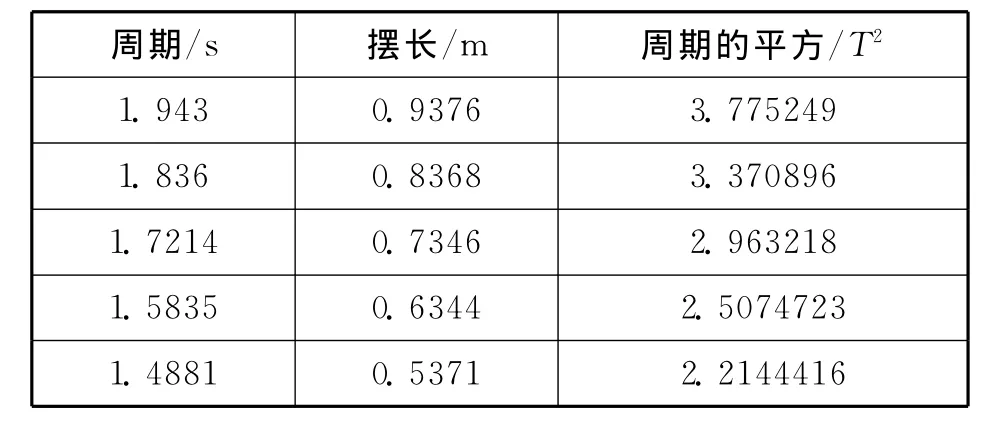
表3

從圖3中我們發現T2－L圖像是一條直線，從而證明猜想是正確的，也說明對數法在解決這類問題時是可行的.

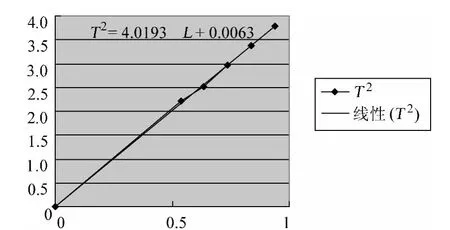
圖3

2.2 對數法在探究行星運動周期與半長軸定量關系的應用

上述單擺周期與擺長的關系并不是特別復雜，高中階段我們還學習過開普勒三大定律，其中第三定律的內容是周期與半長軸的關系，關系較為復雜，我們能否通過分析行星的運動規律來得到周期與半長軸的定量關系呢？不妨一試.

問題.如表4所示，這是當年第谷研究行星運動時的數據，請根據數據找到T與a的定量關系.

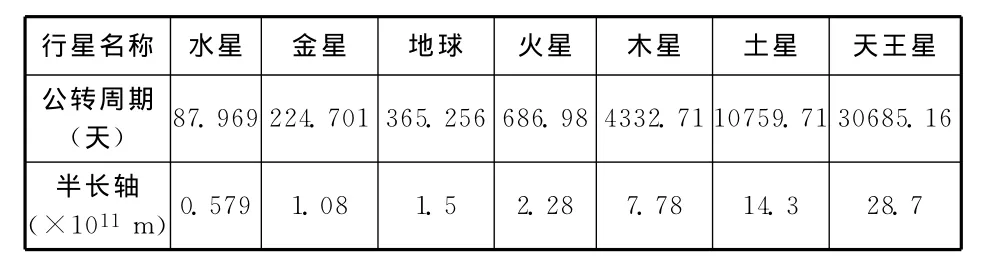
表4

分析：由于數據較大，故可以以水星數據作為參照處理，如表5.

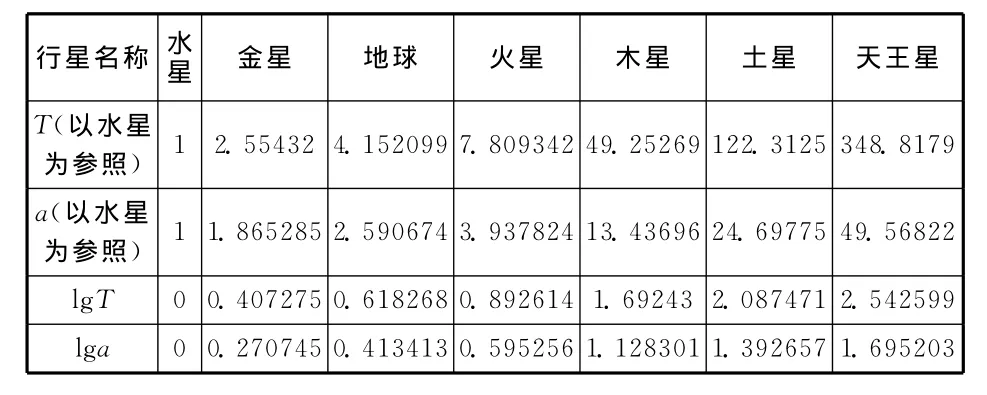
表5

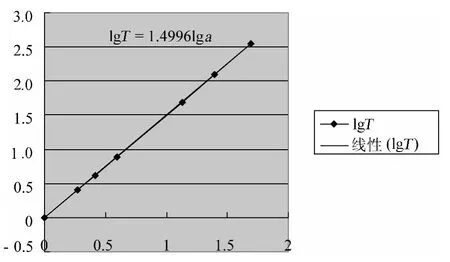
圖4

根據表5的數據，利用Excel軟件畫出lgT－lga的圖像，如圖4所示，從中可以得到斜率為1.4996，這與1.5非常接近，我們可以猜想，猜想是否正確，只要畫出T2－a3的圖像，觀察圖像是不是過原點的一條直線，如果是就證明猜想正確.圖5就是T2－a3的圖像.（注：由于數據范圍太大，我們做以下處理，T和R都以地球為參照，如表6所示，圖像中參照的數據是水、金、地、火4大行星的數據）

表6

從圖5中可發現T2－a3圖像是一條直線，從而證明猜想是正確的.

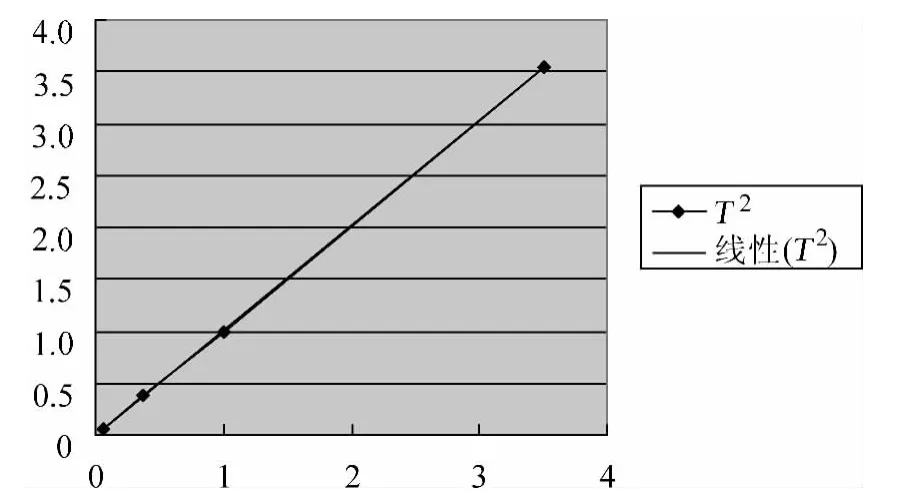
圖5

3 方法總結

通過對兩組實驗數據的分析處理，我們發現利用對數法確實能夠縮短猜想的過程，使得數據處理顯得簡潔明了.當然，由于高中階段遇到的物理量之間的關系一般不是很復雜，所以，我們并不是常用到，但它不失為一種好方法.利用對數法處理數據能夠使得物理量間呈現線性關系，故在求解物理量時也有其妙用，比如我們就可以用對數法處理單擺的實驗數據，求解重力加速度等.由此可見，對數法在具體的應用中有著化難為易、化曲為直、化繁為簡的作用，在高中物理實驗教學中應滲透這種思想方法.

1 趙繼紅.單擺實驗數據處理［J］.太原師范專科學校學報，2001（3）：12－13.

2 林彩欽.用圖解法處理物理實驗數據［J］.物理教師，2013（10）.