船舶擱淺于臺型礁石場景下雙層底縱桁上縱骨變形機理研究

于兆龍，胡志強，2，王 革，姜 哲

（1.上海交通大學海洋工程國家重點實驗室，上海 200240；2.大連理工大學工業裝備結構分析國家重點實驗室，大連 116023；3.美國船級社，新加坡；4.中國海洋石油總公司研究總院，北京）

船舶擱淺于臺型礁石場景下雙層底縱桁上縱骨變形機理研究

于兆龍1，胡志強1，2，王 革3，姜 哲4

（1.上海交通大學海洋工程國家重點實驗室，上海 200240；2.大連理工大學工業裝備結構分析國家重點實驗室，大連 116023；3.美國船級社，新加坡；4.中國海洋石油總公司研究總院，北京）

以典型船舶雙層底結構中縱桁上的縱骨為研究對象，運用塑性力學理論和數值仿真手段，討論了縱桁上骨材在船舶擱淺于臺型礁石場景下的變形過程和破壞機理。研究中應用LS＿DYNA仿真模擬得到結構變形模態和能量耗散結果，在研究變形模態基礎上建立底縱桁骨材塑性變形發展過程的數學模型。運用塑性力學理論求解縱桁上骨材變形吸收的結構變形能和平均變形阻力；同時，應用數值仿真結果進行驗證。研究得到的縱桁骨材變形阻力和變形能解析計算公式，對船舶雙層底耐撞性結構設計和耐撞性能評估都具有一定的指導意義。

船舶擱淺；底縱桁骨材；解析計算；數值仿真；結構變形能

近幾十年來伴隨著海上航行的船舶數量不斷增加，船舶擱淺、觸礁和碰撞事故的發生也愈發頻繁。嚴重的船舶碰撞與擱淺事故會造成巨大的經濟損失和人員傷亡，同時還會引發環境污染等生態災難，最為著名的是1989年發生在美國阿拉斯加的Exxon Valdez號油輪擱淺事故，引發大量的原油泄漏，成為人類海運史上最具破壞性的人造生態災難。為了將船舶因此類碰撞和擱淺造成的損失降到最低，船舶設計中需要針對船舶抗撞性能提出更多的理性設計標準來評估船舶安全性能。為此，研究人員［1］在評估船舶結構響應上投入了大量的研究工作，提出很多創新性的概念和方法，并最終應用于船舶初步設計當中。

評估船體結構響應的方法主要有四種：簡化解析法，模型試驗，實船實驗和數值仿真。其中簡化解析法具有計算周期短、結構變形破壞模態易觀察、結果精度較高等優點，適合應用于船舶初步設計和碰撞事故應急處理。簡化解析法的提出一般是基于實船事故、模型試驗和數值仿真得到的破壞變形模態建立的。破壞變形模態很大程度上和礁石的形狀相關［2］，其中對臺形礁石研究相對較少。Hong等［3］提出一種油輪擱淺于臺型礁石時雙層底板材構件（縱桁、肋板和外底板）變形模態的數學模型并給出其結構變形能解析式。該方法對船舶觸礁擱淺事故緊急處理和船舶防撞性設計具有一定的意義。然而，該方法中并沒有考慮相關骨材的作用。骨材構件通過與板材構件焊接為一個整體從而提高結構整體的強度和剛度。傳統的處理骨材的方法是Paik［4］提出的等效板厚法，即將骨材截面分攤到被依附的板上，通過被依附板的厚度的增加來代替骨材的作用，這一方法可以粗略的估算骨材的作用。然而，Hu等［5］通過研究證明在船舶擱淺于臺型礁石時，這種方法明顯低估了骨材的作用，其后劉毅等［6］針對這一問題運用數值方法確定了等效板厚法在臺型礁石擱淺時的有效系數，不過這種方法還是不能從本質上解決問題。因此，本文通過對數值模擬的變形模態進行分析，運用塑性理論對雙層底縱桁上骨材的變形模態和破壞機理進行研究，得到骨材變形能和變形阻力解析計算公式，并通過數值仿真結果驗證，所得到的結論對擱淺場景下船舶耐撞性結構設計和船舶的耐撞性能評估都具有一定的指導意義。

1 問題描述

Hong等［3］給出了在不考慮骨材情況下，船舶擱淺于臺型礁石時雙層底結構的變形模態和結構響應的解析式。然而，對于真實船舶，骨材顯著地增加了結構剛度從而幫助抵抗外載荷的作用。典型的油輪雙層底結構（帶骨材）如圖1所示，主要包括3部分：外底板、船底縱桁和肋板，撞擊情景如圖1所示。

圖1 典型油輪雙層底結構及撞擊場景示意圖Fig.1 A typical double bottom structure with stiffeners

本文研究縱桁上的骨材在雙層底油輪擱淺于臺型礁石場景下的結構響應。縱桁上骨材的布置如圖2所示，沿著縱桁高度方向均勻的布置3根縱骨由下到上分別編號為1、2、3，且撞深的增加方向設定為自下而上，即礁石首先接觸到第1號縱骨。同一根縱桁上的一組骨材在擱淺之后的變形模態如圖3（a），其中撞擊深度取為0.7Hb（Hb為雙層底高度）。由圖3可見縱桁上的縱骨具有穩定的變形特征，變形曲線呈振蕩的弧形狀，同時具有明顯的周期性。不同位置的骨材周期相同，但是相位有差異。由圖3（b）可以看到對稱布置的1號和3號骨材在0.7Hb撞深下具有相似的相位。然而由圖3（c），1號與2號骨材具有明顯的相位差，但振幅基本保持一致。

圖2 縱桁上骨材布置圖Fig.2 The arrangement of longitudinal girder attached tiffeners

圖3 縱桁骨材變形模態示意圖Fig.3 The deformation patterns

圖4中給出了縱桁上骨材形成弧形的變形模態的過程。由圖4可見，礁石將骨材擠壓到撞深附近的位置，從而使骨材與未變形的骨材形成一個傾斜的角度。從未變形到被擠壓到撞擊深度的位置，骨材承受強烈的拉伸和彎曲變形，形成最終的弧狀變形。這種傾斜的弧狀變形模式使得同一種撞擊深度下不同垂向位置的骨材在完全與礁石撞擊發生變形時，變形的最大橫向延伸趨于相近。

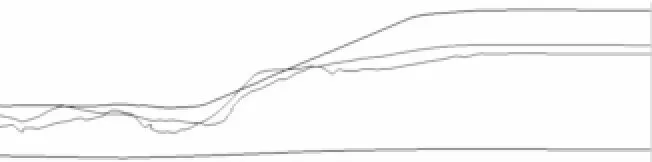
圖4 縱桁上骨材弧狀變形的形成（輪廓模式）Fig.4 The arch-shaped deformation of longitudinal girder stiffeners（edgemode）

現有的船底縱桁構件擱淺于臺型礁石的理論模型的提出都是僅針對有帶板的縱桁單獨作用的情況，并沒有考慮肋板的影響。本文研究針對整個雙層底結構中的縱桁和骨材，因而需要考慮雙層底結構之間的相互作用對變形結果的影響。縱桁與肋板組成的交叉構件明顯增強了交叉點處局部的強度和剛度，對縱桁的變形周期影響比較明顯。通過對LS＿DYNA數值仿真的變形結果進行測量并取平均值，示于表1，其中在模型中肋板間距l＝4 m。

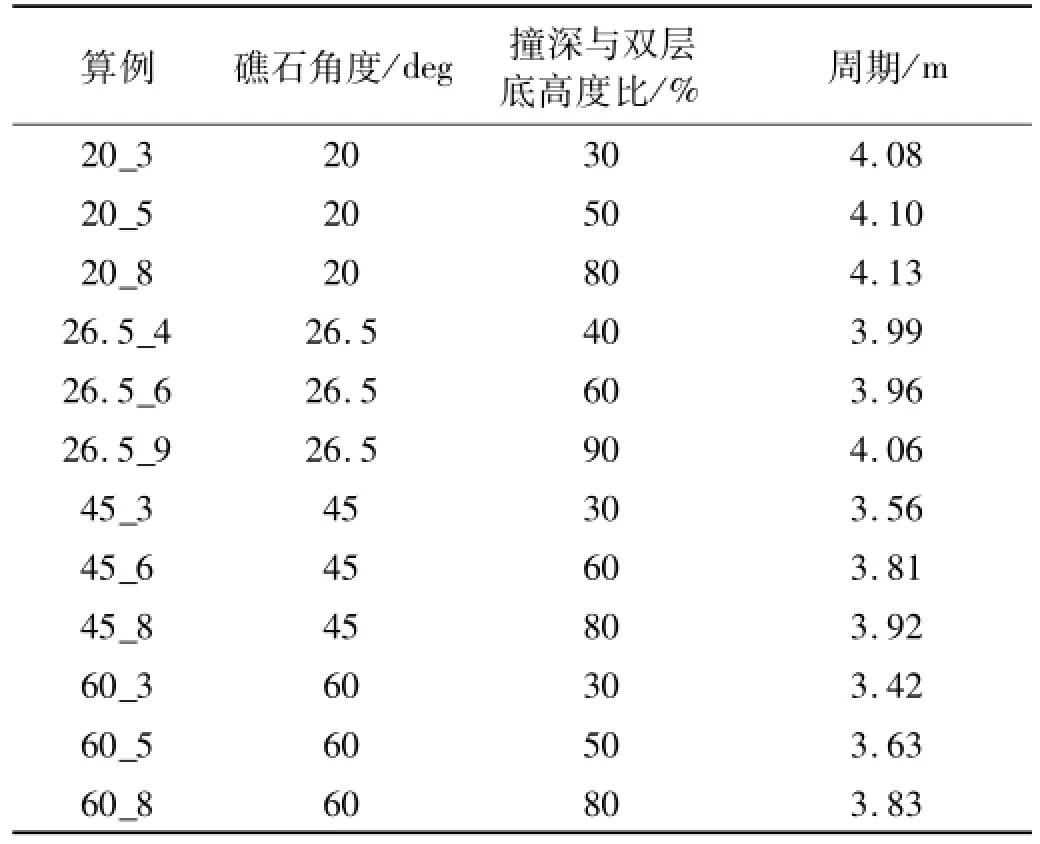
表1 數值仿真中縱桁的變形周期結果Tab.1 The deformation cycle length of longitudinal girders in num erical simulations

表1中算例一欄的含義如下：工況“20＿5”是指礁石角度為20°，撞擊深度與雙層底高度比為0.5的算例，本文其他工況號也應用這一定義。由表1可知，盡管周期隨礁石角度和撞擊深度變化仍呈現一定規律，但縱桁與肋板的交叉結構很大程度的減弱了這種變化規律產生的效果，不同撞深不同角度的周期都趨向于相鄰肋板之間的距離。故在理論模型中假設由于交叉結構的影響，變形周期不隨角度和撞深變化，即：

Lc＝2L＝l（1）

2 研究現狀分析及理論模型的提出

2.1 研究現狀

關于船舶擱淺于臺型礁石情況下的雙層底結構骨材的變形模式和能量耗散的相關研究較少。傳統的方法是依照Paik［4］的等效板厚法近似估算，但結果精度較差。本文從機理上著手對縱桁上骨材結構變形響應進行解析研究。骨材的變形和破壞很大程度上受到其所依附板材的變形影響。Amdahl［7］給出了肋板與縱桁組成的交叉結構在軸向載荷作用下的兩種響應模式：對稱模態和非對稱模態。Simonsen［8］針對船舶擱淺于圓錐形礁石情景下提出了一種移動的變形區域理論，并給出了以薄膜拉伸為主要模式的能量耗散解析式。Midtun等［9］對船舶擱淺于臺型礁石情況下縱桁變形和響應進行機理解析，但是其給出的解析式具有不小的局限性，沒有給出變形角度和周期的解析解，而是根據數值仿真結果擬合得出，其是否適用于不同結構尺寸下的響應估計仍然需要進一步驗證。Hong等［1］在此基礎上進一步研究并提出了一種新的縱桁在臺型礁石擱淺情景下的變形和破壞模式并給出解析解，其變形模態及理論模型如圖5所示。其中，2L為縱桁水平方向的變形周期長度，θ為橫向變形角，2H為垂向擠壓深度，M為邊ab在變形后產生的縱向滑移距離。

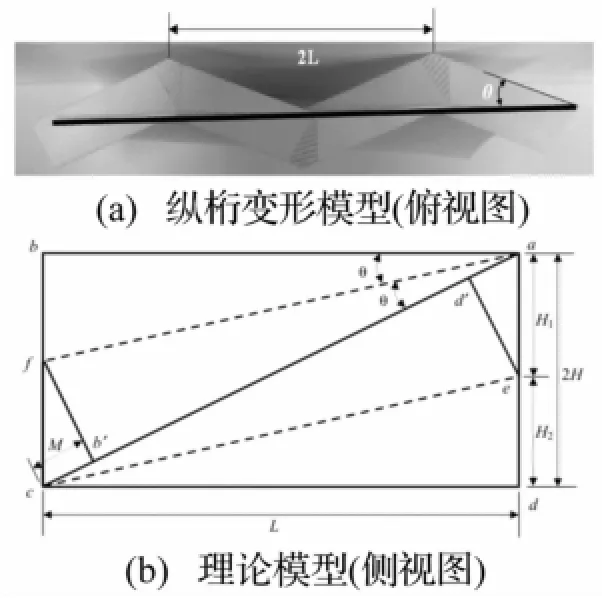
圖5 Hong和Amdahl的縱桁變形的理論模型Fig.5 Hong and Amdahl's theoretical model of longitudinal girders

2.2 Hong和Am dah l的縱桁模型中存在的問題

在Hong和Amdahl［1］的模型中，以一條直線代表縱桁上的骨材（如圖6左所示），變形后結果見圖6右，其中斜線陰影處為膜拉伸能量耗散區域。根據其模型理論，盡管縱桁變形呈周期性振蕩，但骨材變形后仍保持為直線，這并不符合在數值仿真中觀察到的變形結果。同時，Midtun和Amdahl［9］應用數值仿真技術證明了肋板的存在不會影響縱桁變形最大的橫向伸展程度，而只會限制靠近肋板與縱桁交叉處的橫向變形程度。基于這一結果，對數值仿真結果的縱桁橫向變形測量結果對比，以26.5°為例，結果如表2所示。

圖6 紙折法表示Hong和Amdahl的加筋縱桁梁的變形模型Fig.6 Hong and Amdahl's stiffened longitudinal girder deformationmodel by paper folding

由表2可知，數值仿真結果隨撞深增加，橫向變形延伸并沒有非常明顯的增大趨勢，增長趨勢緩慢。因此，Hong和Amdahl的臺型礁石擱淺場景下的縱桁模型的最大橫向伸展距離在很大程度上高估了真實的橫向延伸情況，故該理論模型需要進一步改進。

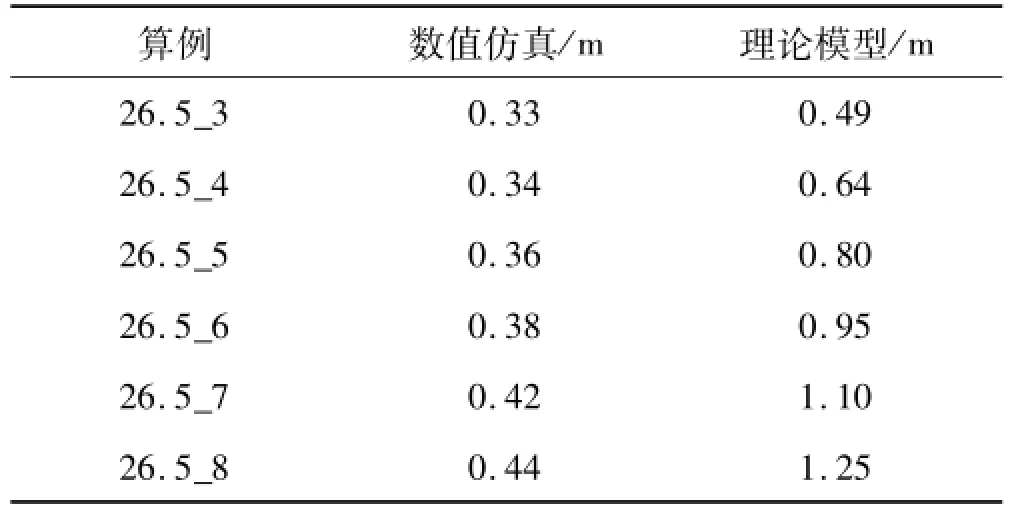
表2 Hong和Am dahl的縱桁模型橫向延伸量的數值對比Tab.2 Transverse extent verification of Hong and Amdahl's longitudinal girder model by numerical simu lations

2.3 新縱桁理論模型的提出

基于以上分析，提出一種新的縱桁變形理論模型，如圖7所示。

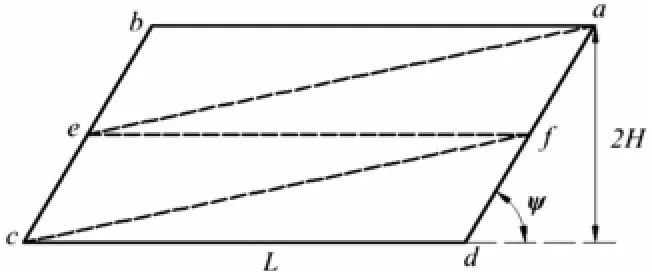
圖7 臺型礁石擱淺情景中一種新的縱桁理論模型Fig.7 A new theoreticalmodel for longitudinal girders during shoal grounding scenario

在新的縱桁變形模型中，縱桁板被ef分為變形模式相同的上下兩部分。塑性絞線ae、cf呈弧形狀，分別彎向縱桁板平面的兩側，這符合數值仿真中橫截面的觀察結果，如圖8所示。

圖8 典型縱桁截面的變形過程Fig.8 Folding process of a typical cross section of the girder

圖8中E點對應著圖7中的折痕ef，ef也是一條振蕩曲線，與上下兩部分的折痕相位相差π／2，圖8中的E點為其正好振蕩到平衡位置。這一結論可以圖3中得到證實。

新縱桁模型的橫向伸展的數值和理論結果對比如表3，數值結果顯示隨著撞深每增加0.1Hm＝0.268，橫向變形伸展僅增加0.02 m，這充分說明垂向的變形初始為2個對稱模態，但并不局限于兩個近似的對稱模態，而隨著撞深的增加可能存在更多的模態。即當撞深增加到一定程度設為2H0時，橫向延伸不再增加，而是在垂向開始了另一個新的垂向變形周期。

表3 新縱桁板材模型橫向延伸距離的數值對比驗證Tab.3 Transverse extentvalidation of the new longitudinal girder model by numerical simulations

基于這一新的縱桁理論模型，可以得到縱桁骨材的最大的橫向伸展距離為：

撞深和礁石角度影響公式，可以采用Hong和Amdahl的模型中計算公式：

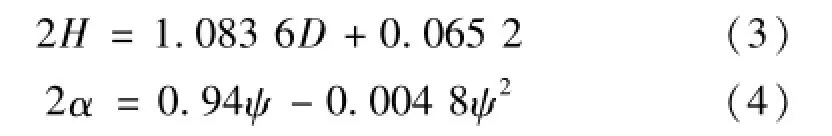
其中：D為撞擊深度，ψ為礁石的角度。

3 縱桁的縱骨變形機理解析計算

圖3中給出了縱桁上骨材在臺型礁石擱淺中的變形模態，通過數值模擬結果的觀察分析發現骨材的變形可分為兩種：與礁石完全接觸的縱骨碰撞變形和尚未接觸礁石產生的波及變形。本文旨在詳細闡述縱骨完全碰撞情況下的變形機理，其能量耗散方式主要有三種：

（1）縱骨弧形狀變形的彎曲能量

（2）縱骨弧形狀變形的膜拉伸能量

（3）縱骨在垂向被礁石擠壓彎曲的能量

三種能量耗散方式在下面做詳細闡述。傳統的金屬在變形做功過程中會發生硬化現象，流動應力會大于初始屈服應力σy小于極限抗拉強度σu，因此取流動應力σ0＝（σy＋σu）／2［10］。從能量耗散模式上來看，耗散模式主要有兩種即彎曲能量Eb和膜拉伸能量Em。

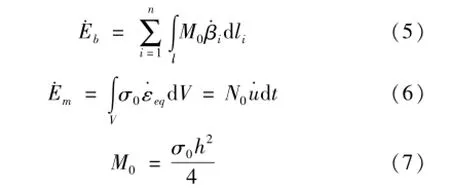
N0＝σ0A（8）

其中：σ0為流動應力，ε·eq為等效應變率，為主應變率。和l分別為經過第i根塑性絞線的角速度和第i根絞線的長度。

3.1 與礁石完全接觸的縱骨變形機理

根據數值仿真結果的觀察和新縱桁模型理論，提出如圖9中所示的半個周期的縱骨骨材變形理論模型。圓柱形的外輪廓保證在不同位置上骨材的最大橫向延伸變形相同。縱骨變形呈螺旋狀上升，螺旋傾角為α。

圖9 縱骨變形理論模型Fig.9 Theoreticalmodel of the deformed stiffener

如圖9所示，骨材AB原長為L，拱形的高位h，則有：

由于傾斜的骨材弧形變形對應的為橢圓形狀，為方便計算彎曲能量這里采用圓形近似其圓心角用∠AOB相似（由于膜拉伸為最主要的能量耗散方式，這一近似計算得到的彎曲能量對整體影響不大）。經過塑性變形后骨材由于拉伸而變長，則骨材伸長長度為：

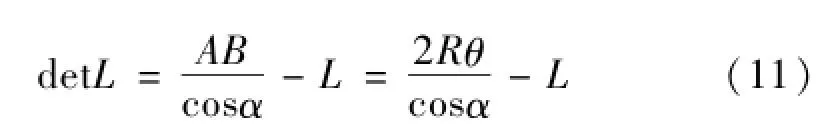
則圓弧變形的膜拉伸能量為：

圓弧變形的彎曲能量為：

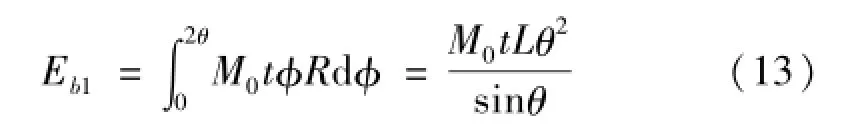
其中t為骨材的厚度。

圖9中討論的是半個周期內的縱骨變形，但從局部來看，由于礁石擠壓引起縱骨垂直方向上產生的位移是緊貼礁石前壁的，因而形成的局部垂向彎曲角度即為礁石角度φ，其彎曲能量為：

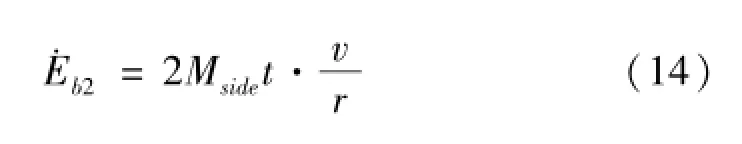
其中Mside＝σ0t2／4，對于r的取值參見Yu等［11］得：r＝1／ψ，則對于半周期：

Eb2＝2MsidetLψ（15）

綜上半周期內縱骨耗散的能量為：

EL＝Eb1＋Eb2＋Em（16）

3.2 碰撞力

基于變形分析和塑性理論已經建立了縱桁縱骨在兩種情況下的能量耗散解析式。能量吸收主要由水平力和垂直力共同做功。水平內力FH，plasticity（塑性水平力）和垂直內力FV，plasticity（塑性垂直力）與礁石角度直接相關，如圖10，表達式如下：

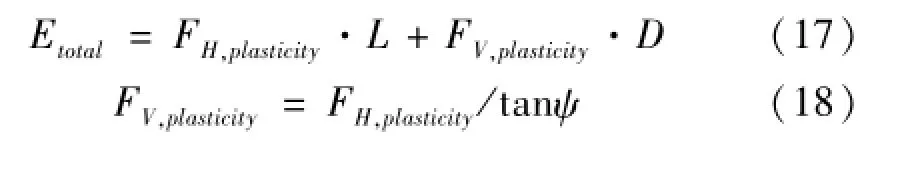
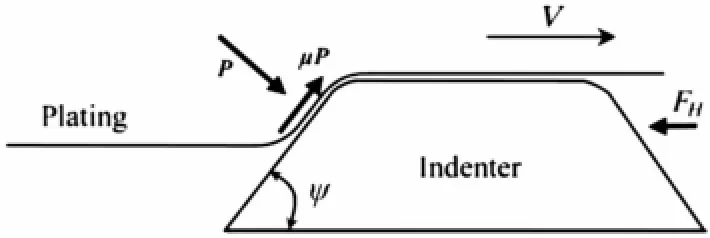
圖10 礁石受力情況Fig.10 Grounding resistances on the indenter（Hong 2011）

水平方向基于力的平衡，FH得到：

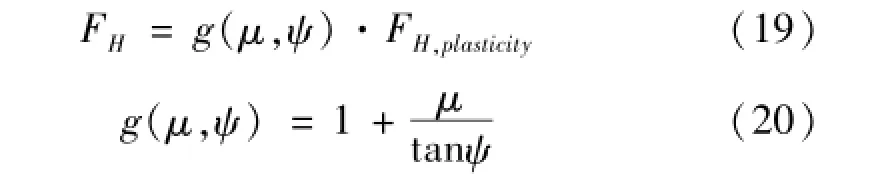
參數g（μ，ψ）最先由Ohtsubo等［12］提出，用來計算船底板撕裂時的摩擦效應。然后，可得FV：

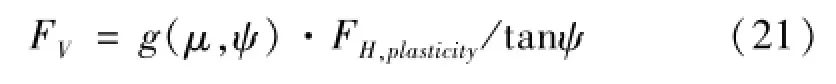
其中：FH和FV分別為水平力和垂直力。

4 數值仿真驗證模型

4.1 模型描述

本文以一艘140 000 t穿梭油輪平行中體的一個分段作為研究對象，進行雙層底結構數值仿真研究。其側視圖見圖11，油船主要結構尺寸見表4。擱淺的場景如圖1所示，礁石為具有較大的接觸面積，截面為梯形的臺型礁石。這類礁石與傳統的有尖銳棱角的礁石相比，不會造成結構或板的撕裂，卻更容易通過使結構發生變形從而降低整體的抗彎剛度和強度，因此值得深入研究［3］。

圖11 油船型線的側視圖Fig.11 A side view of the tanker

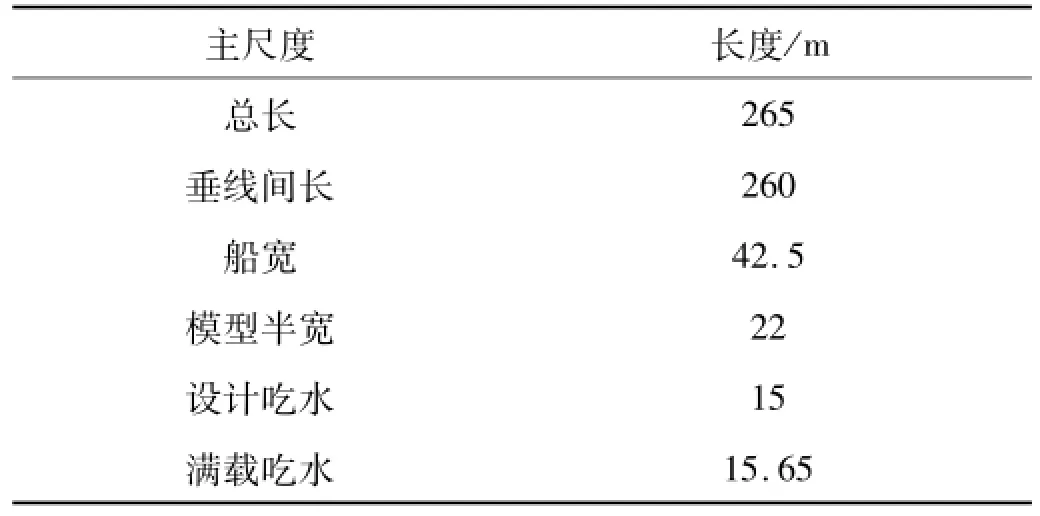
表4 油輪的主尺度Tab.4 Scantlings of the shutter tanker

4.2 有限元模型及仿真算例

數值仿真過程采用PATRAN2008r2進行船體艙段建模并應用非線性動力學軟件LS＿DYNA971進行計算。油船的有限元模型如圖12所示，該艙段模型主要采用了四邊形Belytschko7－Tsay（ELFORM2）單元，模型共劃分了299 586個單元。艙段模型縱向延伸到兩個橫艙壁處，橫向連接舷側外板，因此艙段的內部結構有足夠大的空間在礁石模型的撞擊中發生完整穩定的變形［13］。為了提高計算精度和效率，有限元模型網格疏密結合。對可能發生接觸的雙層底區域精細模擬，其它區域為粗網格，并由細網格部分逐漸過渡到粗網格部分。為了研究不同垂向高度下的縱桁骨材吸收能量的情況，不同高度骨材被分開成不同的部分并編號如圖2。

圖12 雙層底油船的有限元模型Fig.12 Finite elementmodel of the double bottom tanker

艙段模型在兩端固定并忽略船體運動的影響，通過礁石模型移動完成擱淺模擬。擱淺過程中結構采用自接觸和主從接觸相結合。摩擦系數取為0.3，縱桁的高度即雙層底的高度為Hb＝2.68 m，板厚為20 mm；相應的縱桁上的骨材高度為h＝250 mm，厚度為t＝10 mm。

為了全面地對提出的解析方法進行驗證，數值仿真計算涵蓋較廣的礁石角度和不同的撞擊深度。因為海底障礙物為臺型礁石，所以礁石的角度不應太大（否則礁石會變為尖銳棱角狀，產生撕裂，從而不適用本方法）。從保守角度來考慮，礁石的角度分別選取為20°，26.5°，45°和60°，對應于每一個礁石角度，選取10%Hb－90%Hb的雙層底高度進行驗證。

5 數值仿真驗證結果和討論

5.1 數值仿真結果與分析

本文采用數值仿真技術對提出的縱桁縱骨在臺型礁石擱淺場景下的理論模型進行驗證和討論。表5中列出了同一根縱桁上的3根處于不同高度的骨材能量耗散的數值仿真結果。

表5 同一縱桁上3根骨材的能量耗散數值仿真結果Tab.5Numerical energy dissipation of three different stiffeners in vertical direction on a girder

表5中加粗的數字表示與礁石完全接觸變形的縱骨能量，未加粗的數字為波及變形產生的縱骨能量。可見，1號縱骨變形能量基本上為縱骨完全接觸變形產生的，2、3號縱骨變形大部分為未接觸礁石而由能量傳遞產生的波及變形產生的。由1號縱骨變形能結果可見，骨材在同一角度不同撞深時的能量耗散變化趨勢不明顯。小撞深時，隨撞深增加而縱骨能量增加，當增加到一定程度時，撞深繼續增加而能量反而有減小的趨勢。但總體來說能量變化不大，基本穩定在一個值附近。觀察0.8Hb，0.9Hb情況下三種縱骨都達到完全接觸變性，同一角度下三者的值比較接近，第三號縱骨變形值略小。這主要是由于垂向新的變形周期尚未完全形成，橫向伸展尚未達到最大。

縱桁的縱骨中有一些并未與礁石發生直接接觸，但由于縱桁變形的能量傳遞效應，這類縱骨也會發生間接變形。圖13中給出了算例45＿5中三種不同高度下的骨材能量耗散隨撞深的變化趨勢。

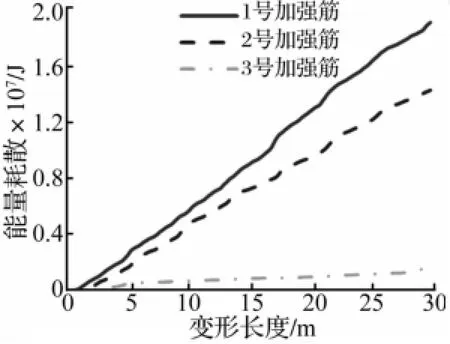
圖13 45＿5中三根不同位置縱骨數值能量－變形長度曲線Fig.13 Numerical energy dissipation-crushing length curves of three vertically different stiffeners for case 45＿5

由上圖可見，骨材由于能量傳遞產生的波及變形，其能量耗散與完全碰撞下模態相同，仍保持線性變化。由圖3觀察可得二者的變形周期亦保持一致。唯一的區別是變形的橫向最大伸展在不斷縮小，因其整體能量減小，如表5所示。波及變形的能量耗散詳細變形機理有待進一步研究。

5.2 縱骨理論公式數值驗證

圖7中的新的縱桁變形模型上下對稱，然而隨著撞深的增加，在垂直方向上還可能會出現更多的變形周期，因而H0的取值很重要。以上理論不能給出H0的閉式解析解，基于數值仿真給出經驗解為：

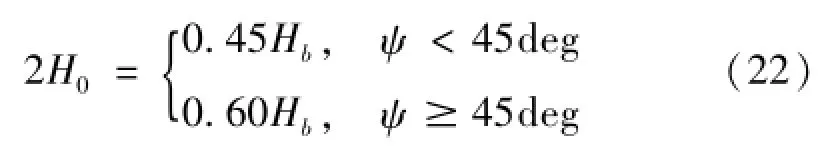
當D＜＝2H0時，直接代入理論公式求解。當撞深增加到D＞2H0時，應將D換算到2H0范圍之內，再代入理論公式，具體換算方法如下：設Hs為縱骨由下而上的垂向高度位置，當D－Hs＜H0時，則2H＝H0＋D－Hs；當D－Hs≥H0時，則說明該縱骨跨越至少兩個不同垂向變形周期的縱骨，其橫向伸展必然會達到最大值，則整體的變形的能量將不再發生變化，此時即2H＝2H0。根據以上說明得到理論解和數值解的對比結果如表6所示。

其中誤差的定義為：

誤差＝（E理論－E數值）／E數值×100%（23）

由表6可見，不同垂向位置的縱骨的理論模型能量耗散結果與數值仿真的接過符合情況良好：能量誤差大部分處于±10%以內，最大誤差不超過30%。在圖14給出了算例45＿5中1號骨材完全接觸下的能量耗散曲線的數值仿真與理論計算數值隨撞深變化的情況。

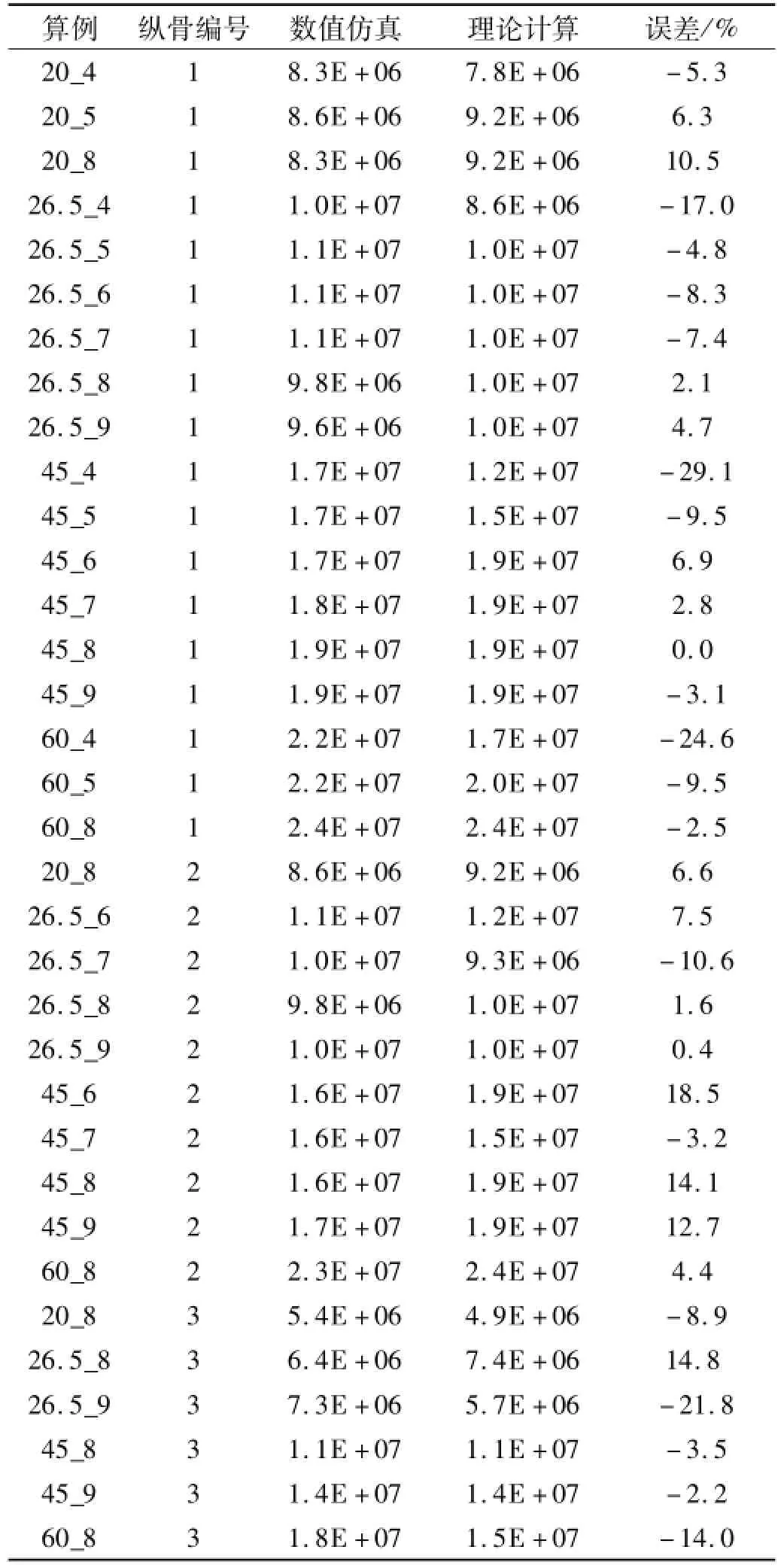
表6 完全變形骨材能量耗散的理論解的數值驗證Tab.6 Theoreticalenergy dissipation of fully contacted and deformed stiffeners

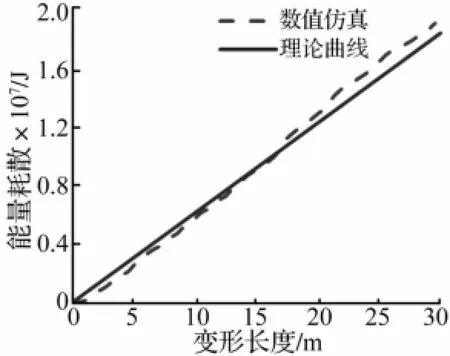
圖14 45＿5中1號骨材理論和數值能量隨撞深變化曲線Fig.14 A comparison of numerical and theoretical energy versus crushing lengthfor stiffener No.1，Case 45＿5

由圖14可見骨材的能量耗散隨撞深變化基本上呈線性增加，新的理論模型和解析計算公式很好的捕捉到了這種趨勢，二者吻合得較好。

6 結 論

本文主要研究船舶擱淺于臺型礁石時雙層底縱桁上骨材的變形和能量耗散機理。研究在分析現有的縱桁變形的理論模型的基礎上，分析了現有模型的不足，并提出新的縱桁變形模型基于新縱桁變形理論模型并結合數值仿真技術計算結果，提出了縱桁骨材變形的理論模型。

礁石在雙層底中滑移時，縱桁上骨材發生穩定的變形，能量耗散方式主要有三種：縱骨的弧形狀變形的彎曲能量、縱骨的弧形狀變形的膜拉伸能量和縱骨在垂向被礁石擠壓彎曲的能量，其中，膜拉伸吸收能量最多。由于肋板與縱桁的交叉結構提升交叉處局部的強度和剛度，使得不同角度和撞深下的縱骨變性周期趨于相同，為肋板的間距。縱桁和其上的縱骨由于礁石擠壓，局部形成傾斜的圓弧狀的變形，使得在同一撞深下不同垂向位置的骨材完全變形后的變形的最大橫向延伸距離基本相同。

應用塑性理論對縱骨變形模型進行分析，得到完全碰撞變形時的能量耗散和擱淺力。數值仿真結果顯示同一位置處的縱骨在完全變形下數值隨撞深變化趨于穩定，但對于不同位置的縱骨，同一撞深完全變形后的能量有差異。理論模型通過垂向周期理論很好的解釋這種現象，理論解和數值結果吻合良好。

由于能量傳遞，未與礁石直接接觸的縱骨會發生波及變形，其能量耗散模式仍保持線性，變形模態和周期與完全碰撞時保持一致，但變形的最大橫向伸展逐漸減小，有關機理有待進一步研究。

［1］Hong L，Amdahl J.Plastic mechanism analysis of the resistance of ship longitudinal girders in grounding and collision［J］.Ships and Offshore Structures，2008，3（3）：159－171.

［2］Alsos H S，Amdahl，J.On the resistance of tanker bottom structures during stranding［J］.Marine Structure，2007，20（4）：218－237.

［3］Hong L，Amdahl J.Rapid assessment of ship grounding over large contact surfaces［C］.In：Proceeding of 5th InternationalConference on collision and grounding of ships；2010.June 14th－16th，Espoo，Finland，2010.

［4］Paik J K.On Qusai-Static crushing of a stiffened squared tube［J］.Journal of Ship Research，1996，40（3）：258－267.

［5］Hu ZQ，Amdahl J.A study on the effectofplate stiffeners of double bottom during ship grounding with large contact surface［C］.OMAE2011－49056 June，2011，Rotterdam，THE NETHERLANDS.

［6］劉 毅，王 晉，胡志強.船舶擱淺于臺型礁石中的等效板厚法的研究［J］.工程力學，2013，30（8）：287－293.

LIU Yi，WANG Jin，HU Zhi-qiang.Investigation on smeared thicknessmethod for ship grounding over obstacles with large contact surfaces and trapezoidal cross section［J］，Engineering Mechanics，2013，30（8）：287－293.

［7］Amdahl J.Energy absorption in ship-platform impacts［PhDthesis］.［Trondheim（Norway）］：Department of Marine Technology，Norwegian University of Science and Technology，1983.

［8］Simonsen B C.Ship grounding on rock－I.Theory［J］.Marine Structures，1997（10）：519－562.

［9］Midtun，Amdahl J.Analysis of tankers during grounding and collision［Master thesis］.［Trondheim］：Department of Marine Technology，Norwegian University of Science and Technology，2006.

［10］Bo CerupSimonsen，Hanson Ocakli.Experiment and theory on deck and girder crushing［J］.Thin-Walled Structures，1999，34：195－216.

［11］Yu Z L，Hu Z Q.Plastic mechanism analysis of structural performances for stiffeners on outer bottom plate during shoal grounding accident［C］.ICCGS2013，June 17th－19 th，Trondheim Norway.

［12］Ohtsubo H，Wang G.An upper-bound solution to the problem of plate tearing［J］.Journal of Marine Science and Technology，1995，1：46－51.

［13］Hu Z Q，Amdahl J，Hong L.Verification of a simp lified analytical methodfor predictionsof ship groundings over large contact surfaces by numericalsimulations［J］.Marine Structures，2011，24：436－45.

Collapsemechanism of longitudinalweb girder attached stiffeners in a shoal grounding scenario of a double bottom tanker

YU Zhao-long1，HU Zhi-qiang1，2，WANGGe3，JIANG Zhe4
（1.State Key Lab of Ocean Engineering，Shanghai Jiaotong University，Shanghai200240，China；2.State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116023，China；3.American Bureau of Shipping，Singapore；4.CNOOC Research Institute，Beijing，China）

Plastic theory and numerical simulation were used to discuss deformation patterns and collapse mechanism of longitudinal web girder attached stiffeners in a shoal grounding scenario of a double bottom tanker.Numerical simulation code LS＿DYNA was used to calculate the deformation patterns and energy dissipation，and a mathematicalmodel of a progressively deforming stiffener was built.With the plastic theory，the deformation energy and themean grounding resistances were solved，and these results were verified with the numerical simulation method.The analytical calculation formulas obtained could be used to calculate and assess the crashworthiness of a ship during its design phase.

shoal grounding；longitudinal web girder attached stiffeners；analytical calculation；numerical simulation；deformation energy

U661.7

A

上海交通大學海洋工程國家重點實驗室青年創新基金課題（GKZD010056－12）；ABSCOTC＆SJTU合作項目

2013－01－17 修改稿收到日期：2013－03－23

于兆龍男，碩士生，1989年生

胡志強男，副教授，1975年生