由逐差法得到的答案是唯一的嗎
——2014年高考福建理綜卷一道實驗題的答案值得商榷

石睿

（福州市第一中學 福建福州 350108）

由逐差法得到的答案是唯一的嗎
——2014年高考福建理綜卷一道實驗題的答案值得商榷

石睿

（福州市第一中學 福建福州 350108）

圍繞2014年高考福建理綜卷一道實驗題展開，用幾種逐差法和Origin 8．0軟件求解其中第（3）小題答案，得到不同結果，通過對比發現對半分組順序逐差產生誤差最小．但關于逐差法產生誤差的分析已超過了高中生能力范圍，故該題答案的唯一性設置值得商榷．

逐差法 Origin 8．0 高考

1 原題與解析

【原題】［2014年高考福建理綜卷第19題（2）］某研究性學習小組利用伏安法測定某一電池組的電動勢和內阻，實驗原理如圖1所示．

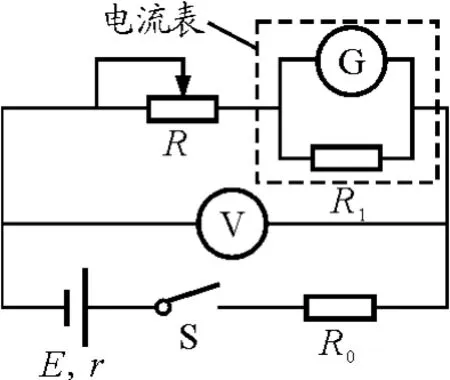
圖1

圖中，虛線框內為用靈敏電流計G改裝的電流表A，V為標準電壓表，E為待測電池組，S為開關，R為滑動變阻器，R0是標稱值為4．0Ω的定值電阻．

（1）已知靈敏電流計G的滿偏電流Ig＝100 μA，內阻rg＝2．0 kΩ，若要改裝后的電流表滿偏電流為200 m A，應并聯一只______Ω（保留一位小數）的定值電阻R1．

（2）根據圖1，用筆畫線代替導線將圖2連接成完整電路．

圖2

（3）某次實驗的數據如表1所示．該小組借鑒“研究勻變速直線運動”實驗中計算加速度的方法（逐差法），計算出電池組的內阻r＝______Ω（保留兩位小數）．為減小偶然誤差，逐差法在數據處理方面體現出的主要優點是______．

表1 某次實驗數據

（4）略．

答案：（1）、（2）略；（3）1．66Ω；充分利用測得的數據；（4）略．

解析：（3）由閉合電路歐姆定律U＝E-Ir′可知，內阻r′為U- I圖線斜率的絕對值，本題中等效內阻r′＝r＋R0，則

由式（1）、（2）、（3），并代入數據得

保留兩位小數，得

2 逐差法的不同數據組合方式

2．1 常用對半分組順序逐差

逐差法常用于求一系列測量量的差值的平均值，使用逐差法處理實驗數據一般來說要求滿足兩個條件：

（1）函數具有線性y＝kx＋b或者有多項形式；

（2）自變量是等間距變化［1］．

使用逐差法時，將所有測量量分成兩組，兩組中的數據對減，這樣每個數據只使用一次，可以避免求平均值時數據相消，充分利用了所有數據．

圖3

高中物理教學在“研究勻變速直線運動”實驗中引入了逐差法．學生分析紙帶記錄下的小車的運動，并使用逐差法求小車的加速度．由于紙帶的特殊性，在該實驗中運用的逐差法，往往演變為“兩段法”更加簡便，即將數據對半分成兩組，以圖3中紙帶為例，將數據分為（s1，s2，s3）與（s4，s5，s6）兩組，再將兩組中的數據按順序分別相減，最終可把紙帶的后一半與前一半看成兩大段相鄰且相等的時間間隔（3T），求出加速度．

顯而易見，上面所附的本題解析中使用的數據處理方法也是對半分組順序逐差．

2．2 用其他組合方式求解本題

本題不像紙帶有前半段后半段之分，單從充分利用數據的角度，完全可以采用其他的數據組合方式進行逐差法，下面試用其他組合方式的逐差法求解此題．

2．2．1 奇偶分組順序逐差

把測量次數為奇數的數據作為一組，測量次數為偶數的作為另一組．

由式（1）、（2）、（4）得

保留兩位小數，得r＝1．63Ω．

2．2．2 對半分組頭尾逐差

仍把數據對半分組，但第二組的最后一個數據減第一組的第一個數據，以此類推．

由（1）、（2）、（5）式得

保留兩位小數，得r＝1．60Ω．

由此可見，同樣是逐差法，利用了所有數據，選擇不同的數據組合方式，會求出不同的答案．但是本題給出的答案是唯一的，即對半分組順序逐差求出的結果．

為什么使用逐差法時都默認使用對半分組順序逐差呢？上述3種組合方式從充分利用數據的角度，應都是可行的．判斷它們優劣應看哪一種分組的逐差法計算結果更接近真實值．

3 使用Origin 8．0處理實驗數據

Origin是美國Microcal公司推出的數據分析和繪圖軟件，具有數據的排序、調整、計算、統計、頻譜變換、曲線擬合等各種完善的數學分析功能，在教學、科研、工程技術領域有非常廣泛的應用．該軟件在擬合直線時，采用最小二乘法作為計算內核，得到的結果相對比較精確．下面筆者使用Origin 8．0軟件，處理題中數據，描繪U- I圖線，擬合直線，并求該直線斜率的絕對值，進而求出內阻，以此作為參考值．

3．1 操作步驟

（1）打開軟件，輸入實驗數據（采用國際單位制），如圖4所示．

圖4 數據輸入窗口

（2）點擊右下方散點圖快捷鍵，選擇橫縱軸描繪散點圖，如圖5，6所示．

圖5U- I散點圖

圖6 橫縱軸選擇窗口

（3）擬合直線與參數分析

選擇Analysis菜單中的Fit Linear，對圖5進行線性擬合，原圖中新增一條擬合出來的直線，同時直線旁出現擬合參數窗口．

圖7 擬合直線與擬合參數

由圖7擬合參數窗口中可看到，擬合直線的截距（intercept）為a＝5．385 36，其標準差為0．008 51，斜率（slope）為b＝-5．684 52，標準差為0．084 25，線性擬合相關系數R＝0．998 46，說明所測量的數據其擬合直線幾乎全部通過數據點（對于一被擬合的直線來說，相關系數越趨近于1，則說明x與y間的線性關系擬合得越好［2］）．

3．2 結果

由上可知，r′＝5．684 52Ω，可得

4 幾種數據處理方式的結果比較

幾種數據處理方式的結果如表2所示．

表2 幾種數據處理方式的結果

對比之前幾種逐差法的結果，可以看出，對半分組順序逐差得到的結果最接近由Origin 8．0得到的參考值，可見，用逐差法處理這組實驗數據時，采取對半分組順序逐差最合理．

但僅從一組實驗數據的分析上我們不能說這個結論是普遍適用的，還應從測量結果傳遞誤差是否最小的角度驗證．

借鑒文獻［3］的研究結果，在只考慮儀器誤差的情況下，對半逐差順序逐差是求測量值差值的平均值的最優分組，它使得在數據處理的過程中，測量結果的誤差最小．這個結論與我們上面的計算結果相符．

5 結論

在高中教學中講授逐差法是在求紙帶加速度的背景下進行的，由于紙帶的特殊性，逐差法均采用對半分組且順序逐差．而2014年高考福建理綜卷的這道題中，不涉及紙帶，利用逐差法，就應該有多種分組可能，對應得到多個答案．

雖然對半分組順序逐差產生誤差最小，是最優方法，但關于逐差法產生誤差的分析已超過了高中生能力范圍，使用哪一種分組方式不應該是在本題的考查范圍之內．而這道題的標準答案設置為唯一值，即只能采用對半分組順序逐差的方式，筆者認為這道題答案是否唯一值得商榷．

1 唐春紅，唐曙光，劉揚正．逐差法和Origin8．0軟件在牛頓環實驗數據處理中的比較．物理通報，2013（9）：98～100

2 曾貽偉，龔德純，王書穎，汪順義．普通物理實驗教程．北京：北京師范大學出版，1989．40～41

3 黃曙江．逐差法的較優分組．物理通報，1998（4）：7～8

2014- 06- 28）