一種基于短時傅里葉變換的機載SAR自聚焦算法

劉忠勝 李銀偉 韋立登 向茂生

?

一種基于短時傅里葉變換的機載SAR自聚焦算法

劉忠勝*①②李銀偉①②韋立登①向茂生①

①(中國科學院電子學研究所微波成像技術重點實驗室 北京 100190)②(中國科學院大學 北京 100049)

合成孔徑雷達；自聚焦；短時傅里葉變換；信雜比；二次相位誤差

1 引言

非參數化自聚焦方法自提出以來，由于其較好的魯棒性，對大部分場景和誤差函數的適應性以及良好的相位誤差補償效果而得到了廣泛應用。但是，利用該類方法時有一個必要條件：在SAR圖像場景中含有高信雜比(Signal-to-Clutter Ratio, SCR)的強點目標。在散焦圖像中提取強點目標，對其進行方位向逆壓縮及去調頻，然后就可以估計其相位誤差。如果點目標方位向信號的SCR足夠高，此時估計得到的相位誤差就可以認為是待估計的相位誤差[6]。PGA算法對SCR的要求不像PPP那么高，是由于其采用了加窗和加權平均兩項措施[5]。但是，加窗一方面會給信號帶來截斷誤差，另一方面不能濾除處于信號帶寬的干擾。而加權平均是基于所有距離單元內信號具有相同的相位誤差歷史。可是由于從不同距離單元提取的相位誤差具有不同的線性項(點目標方位向位置不同)和常數項(點目標本身相位)，這些估計得到的相位誤差無法直接加權平均。因此，PGA算法將每個距離門內的強點目標循環移位至孔徑中心處以消除其線性項差異，同時采用相位誤差梯度估計相位誤差以去除常數項差異。但是點目標的不精確循環移位會降低加權平均的性能，同時采用相位誤差梯度估計相位誤差會導致SCR的下降。因此PGA算法需要足夠多的強點目標。

2 STFT簡介及其應用

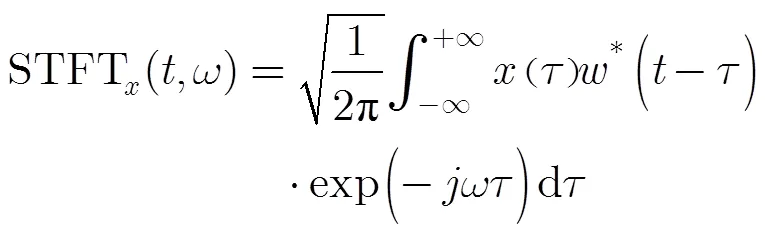
2.1 STFT濾波

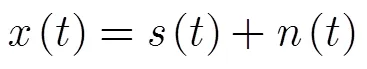
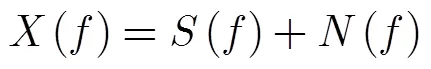
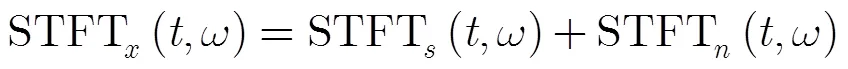
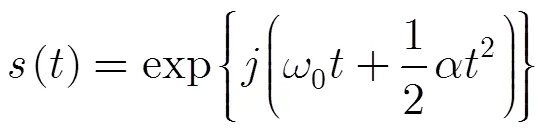
則

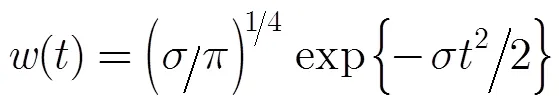
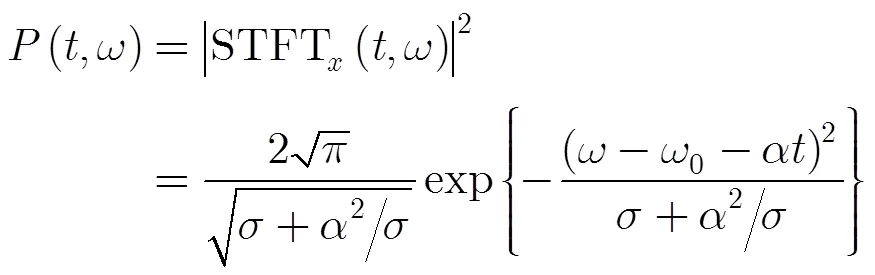
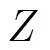
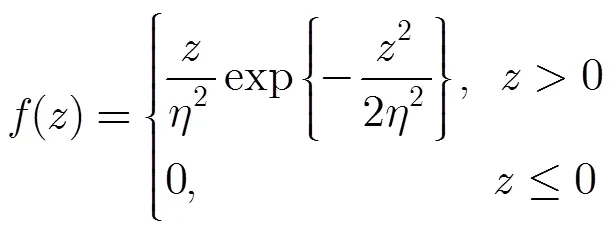
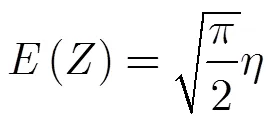
CFAR檢測定義為

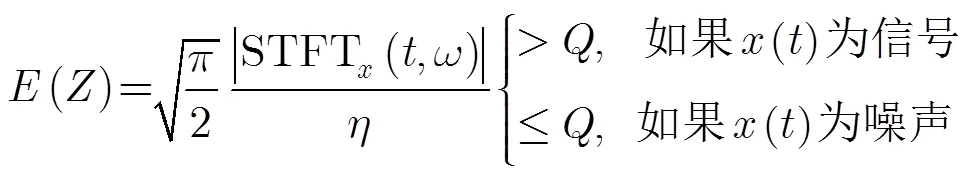
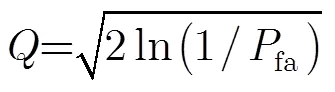
2.2 STFD估計LFM的調頻率

步驟. 1 對信號進行STFT，然后在STFD進行CFAR檢測；

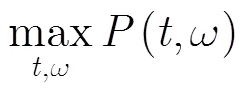
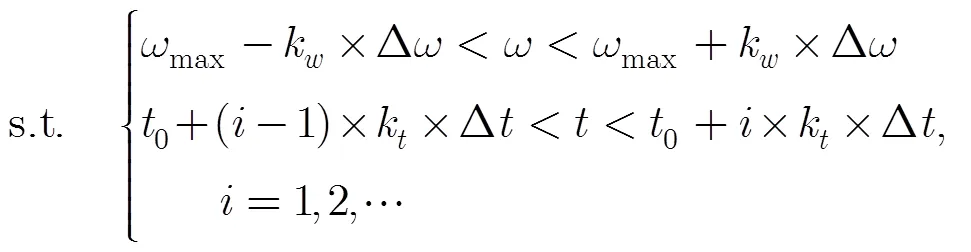
3 STFT自聚焦算法

圖1 STFT濾波與頻域濾波比較

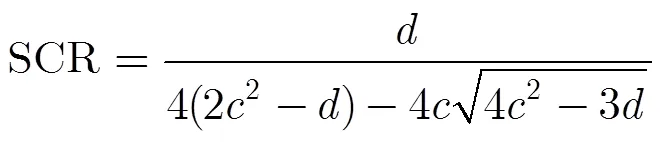
假設經過距離壓縮和距離徙動校正后的點目標信號為

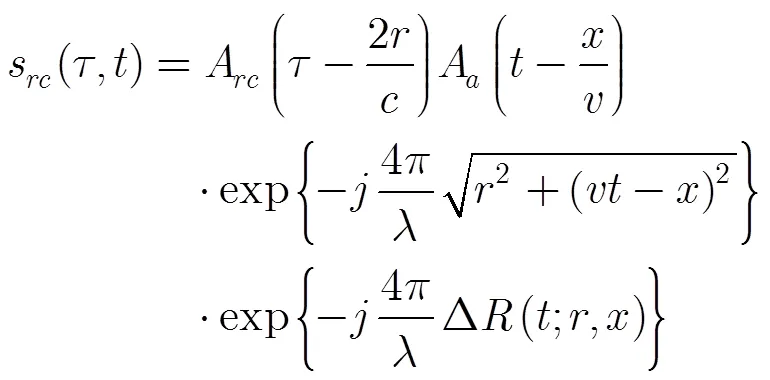
對信號式(16)進行方位去調頻處理，即與式(17)相乘：

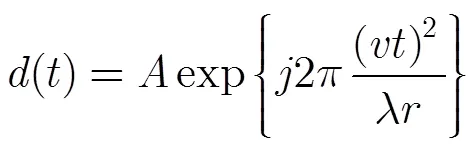
經過方位去調頻處理后，忽略其幅度，式(16)可近似表示為

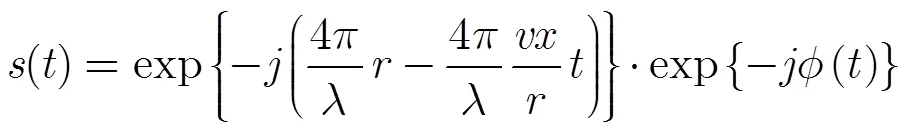
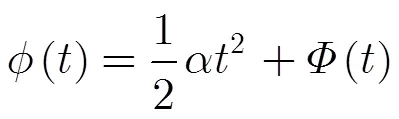
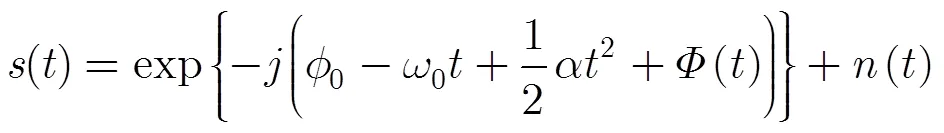
步驟1 根據式(15)進行點目標的自動提取；

步驟2 對點目標進行方位向逆壓縮，然后與式(17)相乘進行方位去調頻；

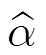
步驟4 對方位向逆壓縮信號進行QPE補償，然后進行方位向壓縮；

步驟5 重復步驟1和步驟2，同時增加SCR閾值，此時式(20)變為

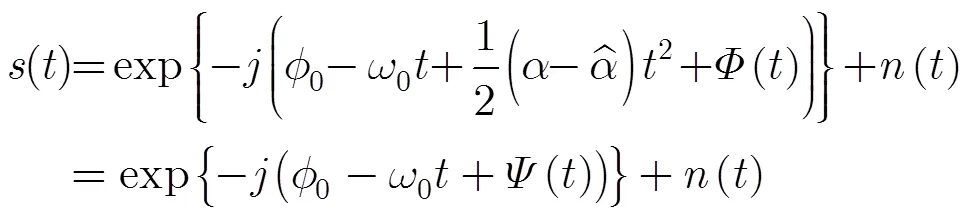
步驟6 對式(21)進行STFT濾波，根據方位信號長度選擇合適的STFT窗長；

步驟7 對濾波后的每個點目標信號進行循環移位，提取其相位誤差梯度，求平均后積分獲得相位誤差；

步驟8 對方位向逆壓縮信號進行殘余相位誤差補償，然后進行方位向壓縮得到聚焦的SAR圖像。

4 實驗數據驗證

4.1 仿真分析

在點目標仿真中，X波段SAR 系統工作在正側視模式，方位分辨率0.5 m，脈沖重復頻率為440 Hz，加入相位誤差量如圖2(a)所示，其具體表達式為

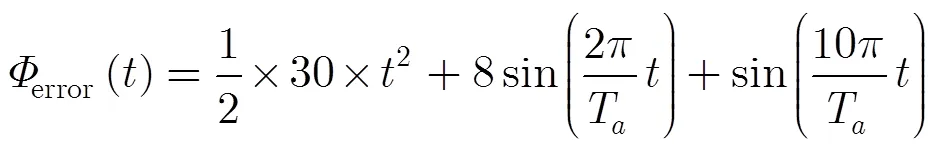
4.2 實際數據處理結果

利用實際SAR數據驗證算法的有效性是必不可少的，在此利用中國科學院電子學研究所X波段機載SAR數據進行處理分析。圖3(a1)~圖3(a3)為3幅散焦圖像，其分別代表了3種不同的場景：含有高SCR的強點目標、含有低SCR的強點目標以及不含有強點目標。圖3(b1)~圖3(b3) 分別為經過PGA[16]處理后得到的SAR圖像，圖3(c1)~圖3(c3)分別為最小熵自聚焦算法[17]得到的SAR圖像，圖3(d1)~圖3(d3)分別為利用本文算法進行自聚焦后的SAR圖像。由圖可知，3幅散焦圖像經過最小熵算法和本文算法處理后圖像質量都得到了較大改善，而PGA處理后的SAR圖像質量依賴于場景類型。當成像場景含有高SCR的強點目標時，PGA能夠獲得與本文算法聚焦質量相當的SAR圖像，如圖3(b1)所示。但是如果成像場景中強點目標的SCR比較低(如圖3(b2)所示)或者強點目標不明顯(如圖3(b3)所示)時，使用PGA算法圖像聚焦質量改善不明顯。由表１所示的最后聚焦圖像的熵值大小可以看出，在具有強點目標的場景，本文算法略優于最小熵算法，而在沒有強點目標的場景，最小熵自聚焦算法適應性更好一些。這也說明了本文提出的STFT自聚焦算法的確提高了信號的SCR，能夠適合于不同場景類型的SAR散焦圖像。同時，與PGA算法需要迭代相比，STFT自聚焦算法不需要迭代就能夠獲得聚焦良好的SAR圖像。通過對多幅散焦圖像的處理，本文算法在SCR大于１dB時均有滿意的聚焦圖像。

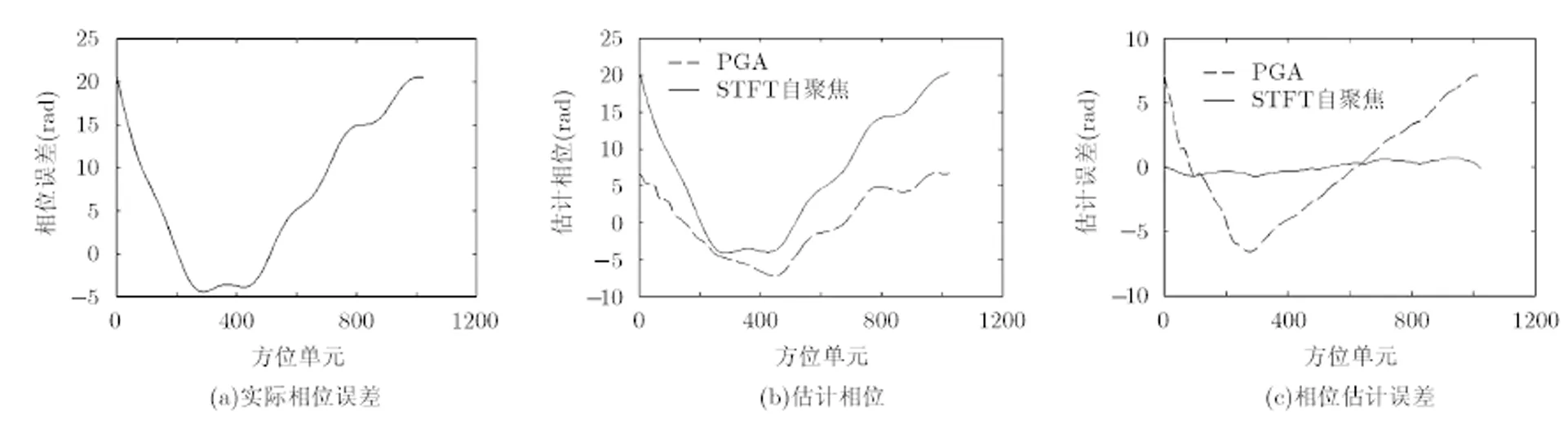
圖2 STFT自聚焦算法與PGA算法性能比較

圖3 PGA、最小熵和STFT自聚焦結果比較

表1幾種算法成像結果熵值比較

序號原始散焦圖像PGA算法最小熵算法本文算法 1 9.1077 7.0953 7.0973 7.0611 210.600910.2381 9.0734 9.0428 313.149213.149312.685012.7144

5 結束語

本文在討論了利用STFT對LFM信號進行濾波及調頻率估計的基礎上，提出了一種基于STFT的機載SAR自聚焦算法。該算法首先利用STFT對QPE進行估計和補償，然后在殘余相位誤差補償時利用STFT濾波器對時變信號進行濾波以提高SCR。對仿真數據和實測數據處理的處理結果驗證了本文算法的有效性和可行性。與PGA算法相比，本文算法能在成像場景中強點目標的SCR比較低或者強點目標不明顯的情況下依然獲得聚焦良好的圖像，同時不需要進行迭代操作。

[1] Fornaro G. Trajectory deviations in airborne SAR: analysis and compensation[J]., 1999, 35(3): 997-1009.

[2] Fornaro G, Franceschetti G, and Perna S. Motion compensation errors: effects on the accuracy of airborne SAR images[J]., 2005, 41(4): 1338-1352.

[3] Berizzi F, Corsini G, Diani M,.. Autofocus of wide azimuth angle SAR images by contrast optimization[C]. Proceedings of the International Geoscience and Remote Sensing Symposium, Lincoln, America, 1996, 2: 1230-1232.

[4] Berizzi F, Martorella M, Cacciamano A,.. A contrast based algorithm for synthetic range-profile motion compensation[J]., 2008, 46(10): 3053-3062.

[6] Berizzi F, Martorella M, Haywood B,.. A survey on ISAR autofocusing techniques[C]. Proceedings of the 2004 IEEE International Conference on Image Processing, Singapore, DOI: 10. 1109/ICIP. 2004. 1418676.

[7] Chen V C and Ling H. Time–frequency Transforms for Radar Imaging and Signal Analysis[M]. Boston: Artech House, 2002: 47-64.

[8] Moreira A and Huang Y H. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J]., 1994, 32(5): 1029-1040.

[9] Owens F J and Murphy M S. A short-time Fourier transform [J]., 1988, 14(1): 3-10.

[10] Pei Soo-chang and Huang Shih-gu. STFT with adaptive window width based on the chirp rate[J]., 2012, 60(8): 4065-4080.

[11] Socheleau F X, Pastor D, and Duret M. On symmetric alpha-stable noise after short-time Fourier transformation[J]., 2013, 20(5): 455-458.

[12] Yin Qin-gbo, Shen Li-ran, Lu Ming-yu,. Selection of optimal window length using STFT for quantitative SNR analysis of LFM signal[J]., 2013, 24(1): 26-35.

[13] Qin Xian-xiang, Zhou Shi-lin, Zou Huan-xin,A CFAR detection algorithm for generalized gamma distributed background in high-resolution SAR images[J]., 2013, 10(4): 806-810.

[14] Tao R, Li Y L, and Wang Y. Short-time fractional Fourier transform and its applications[J]., 2010, 58(5): 2568-2580.

[15] Chan H L and Yeo T S. Noniterative quality phase-gradient autofocus algorithm for spotlight SAR imagery[J]., 1998, 36(5): 1531-1539.

[16] Ye Wei, Yeo Tat-Soon, and Bao Zheng. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus[J]., 1999, 37(5): 2487-2494.

[17] 鄭曉雙. 機載合成孔徑雷達運動補償技術研究[D]. [博士論文], 中國科學院電子學研究所, 2007: 107-111.

Zheng Xiao-shuang, The study of motion compensation of airborne synthetic aperture radar[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Science, 2007: 107-111.

劉忠勝： 男，1977年生，博士生，研究方向為干涉SAR信號處理.

李銀偉： 男，1985年生，博士生，研究方向為SAR成像、運動補償、干涉SAR信號處理.

韋立登： 男，1973年生，副研究員，碩士生導師，研究方向為干涉SAR數據處理技術.

向茂生： 男，1964年生，研究員，博士生導師，研究方向為干涉SAR技術及方法.

A Novel Autofocus Method Based on Short-time Fourier Transform for Airborne SAR

Liu Zhong-sheng*①②Li Yin-wei①②Wei Li-deng①Xiang Mao-sheng①

①(,,,100190,)②(,100049,)

The Short-Time Fourier Transform (STFT) is an important method widely used in the study of the nonstationary signals. After discussing the filtering and the estimation of chirp rate for Linear Frequency Modulation (LFM) signal by using the STFT, this paper proposes a novel autofocus method based on the STFT. The proposed autofocus method firstly utilizes the STFT to estimate and compensate the Quadratic Phase Error (QPE), which is the main part of phase error influencing the quality of the SAR image. And when estimating the residual phase error, the STFT filtering is used for filtering the noise and interference of the time-variant signals to raise the Signal-to-Clutter Ratio (SCR). The experiment results using both simulated data and real data demonstrate the validation of the proposed autofocus method.

SAR; Autofocus; Short-Time Fourier Transform (STFT); Signal-to-Clutter Ratio (SCR); Quadratic Phase Error (QPE)

TN959.73

A

1009-5896(2014)11-2705-06

10.3724/SP.J.1146.2013.02004

劉忠勝 zsliu@mail.ie.ac.cn

2013-12-23收到，2014-06-13改回；

國家重大專項項目(30-H37D01-9004-13/15)和中國科學院裝備研制項目(YZ201107)資助課題