基于源信號包絡矩陣奇異值的機械故障診斷方法
姚春江,毋文峰,陳小虎,蘇勛家
(第二炮兵工程大學,陜西西安 710025)
在旋轉機械設備中,齒輪振動信號具有調制特征,而且幅值調制和相位調制同時存在。一般,機械設備調制信號的包絡更集中地攜帶了機械設備的故障信息,基于調制信號包絡特征的故障診斷方法可準確、迅速地識別機械設備故障。目前,基于調制信號包絡的特征提取和故障診斷方法已經引起了機械設備故障診斷領域眾多學者的關注[1-5]。
在機械故障診斷實踐中,待測部件往往是不可接觸或不能直接觀察和測量的。例如,在齒輪箱診斷中,齒輪和軸承是待測部件,不能直接針對齒輪和軸承本身進行測量,而必須在齒輪箱體或軸承座等可接觸部位進行測量。這樣,測量信號一般是若干個不同的機械部件產生的源信號的混合信號。在機械信號處理中,如何從測量的混合信號中分離或恢復源信號,具有非常重要的意義。盲源分離 (Blind Source Separation,BSS)是信號處理的預處理工具,從機械設備的測量信號中分離出不同機械部件的振動源信號,然后再利用其他的信號處理方法進行深入的處理和診斷。目前,盲源分離已在機械故障診斷領域取得了初步的應用[6-11]。
綜上所述,機械設備的振動信號是調制信號,而且機械測量信號是這些不同源信號的混合信號。盲源分離可從已知的混合信號 (測量信號)中分離出不同的獨立振動源信號,包絡分析是處理調制信號的有力工具。因此,作者將盲源分離和包絡分析相結合,提出基于源信號包絡矩陣奇異值的故障診斷方法,并應用于液壓齒輪泵的故障診斷。
1 基于源信號包絡矩陣奇異值的故障診斷方法
1.1 盲源分離
盲源分離算法[12-13]是基于高階統計量的多元統計分析方法,既可以有效地分離和恢復機械振動源信號,又可以深入機械信號結構,提取機械設備的高階統計特征。在機械故障診斷領域中,盲源分離算法的應用主要集中在兩個方面:一是盲源分離算法可以作為機械信號處理的預處理措施,從已知的混合信號(測量信號)中分離振動源信號,再與其他的特征提取方法聯合,共同提取機械設備故障特征;二是盲源分離可以直接用于提取機械設備的高階統計特征。文中重點研究盲源分離作為預處理措施,與包絡分析和奇異值等傳統方法聯合,共同提取機械設備故障特征。
1.2 包絡分析
包絡分析 (Envelope Analysis,EA)[14],又稱為解調分析,目的是提取載附在高頻信號上的低頻信號,從時域上看,就是提取時域信號波形的包絡軌跡。機械信號的包絡包含了豐富的狀態特征信息,不僅可以反映機械設備有無故障,而且可以反映故障發生的部位和分布等信息。若以機械設備振動信號為研究對象進行解調分析,提取載附在高頻機械振動信號上的與瞬時沖激對應的包絡信號,再進一步分析其時-頻域特征,便可提取齒輪或滾動軸承等機械零部件的故障特征信息,從而可為機械故障診斷提供可靠的依據。
1.3 奇異值分解
在矩陣的奇異值分解 (Singular Value Decomposition,SVD)中,奇異值是矩陣的固有特征,一般,它具有比較好的穩定性,即當矩陣的元素發生小的變動時,矩陣的奇異值變化很小;同時奇異值還具有比例不變性、旋轉不變性和降維壓縮特性等良好性能,因此,矩陣的奇異值符合機械故障診斷對于提取特征的基本要求。
1.4 基于源信號包絡矩陣奇異值的故障診斷方法
綜上所述,提出基于源信號包絡矩陣奇異值的特征提取和故障診斷方法,其流程如圖1所示。
由圖1可知,該方法的具體步驟為:
(1)機械信號測量:從待檢測的機械設備上測量機械設備的多通道傳感器觀測信號;
(2)盲源分離:根據混合信號 (測量信號)分離或恢復機械設備的振動源信號;
(3)源信號包絡分析:提取分離源信號的上、下包絡線并分別組成上包絡矩陣和下包絡矩陣;
(4)包絡矩陣奇異值分解:源信號的上、下包絡矩陣奇異值分解,得到源信號上、下包絡矩陣的奇異值向量;
(5)特征向量提取:源信號上、下包絡矩陣的奇異值首尾相接,組成機械設備的故障特征向量;
(6)模式識別和故障診斷:在提取的故障特征向量的基礎上,引入最小二乘支持向量機 (Least Square Support Vector Machine,LS-SVM)分類器識別和診斷機械設備的故障類型。
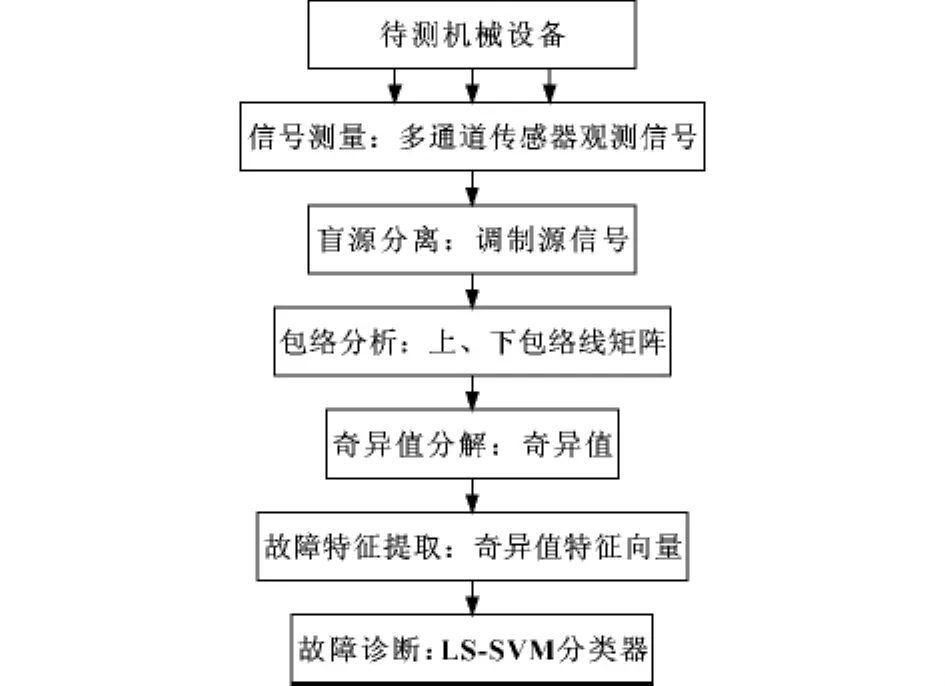
圖1 基于源信號包絡矩陣奇異值的故障診斷方法流程
2 試驗分析
從機械結構和工作原理來看,液壓齒輪泵是一個典型的旋轉機械設備,但是,它又不同于一般的旋轉機械設備,它的工作介質是封閉的液壓油,因此它的工作原理更為復雜,通常的故障特征提取方法難以有效地提取它的故障特征向量。在這里,試將基于源信號包絡矩陣奇異值的故障診斷方法應用于CB-Kp63型液壓齒輪泵。
在實驗室環境下,待檢測CB-Kp63型液壓齒輪泵的振動源信號數量已估計為4個。因此,測量液壓齒輪泵的4通道泵殼振動信號x(t)=[x1(t),x2(t),x3(t),x4(t)]T。液壓齒輪泵試驗臺架和加速度計 (傳感器)的設置如圖2所示,其中,泵軸轉速為定速1 480 r/min。

圖2 液壓齒輪泵試驗臺架及加速度計設置
在此,設定液壓齒輪泵的故障模式類型包括:正常狀態,齒面磨損故障和軸承故障等3種;液壓齒輪泵殼振動信號采樣頻率為10 kHz,采樣時間為1 s,在泵的每個故障模式下各采集64組傳感器觀測信號,即每個故障模式各具有64組4通道測量信號。
液壓齒輪泵的4通道振動信號x(t)=[x1(t),x2(t),x3(t),x4(t)]T去均值和白化等預處理后,應用FastICA算法進行盲源分離,得到分離源信號s(t)=[s1(t),s2(t),s3(t),s4(t)]T。進一步,從各個分離源信號中提取其上、下包絡線,并分別組成上包絡矩陣和下包絡矩陣,其中的一組分離源信號s(t)及其上、下包絡信號的時域波形 (圖中波形為信號的前1 024個點)如圖3所示。
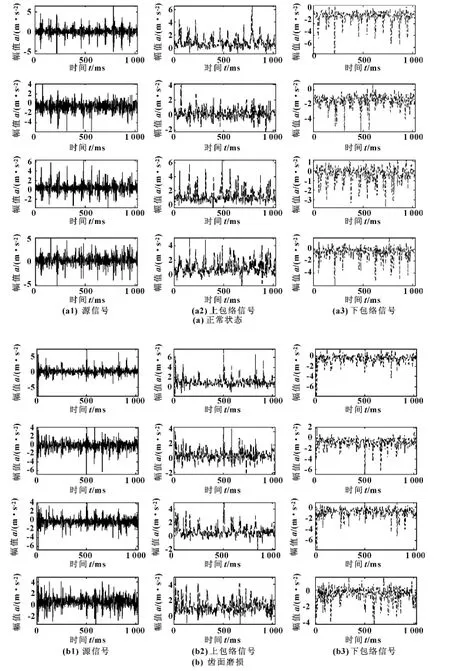

圖3 齒輪泵源信號及其上、下包絡線信號
源信號的上、下包絡矩陣進行奇異值分解,分別得到相應的奇異值向量,,,和,,,,其中,上標“1”代表上包絡矩陣的奇異值向量,上標“2”代表下包絡矩陣的奇異值向量。表1所示為在液壓齒輪泵不同故障模式下提取的奇異值特征向量,限于篇幅,僅列出了其中的5組樣本。源信號上、下包絡矩陣的奇異值首尾相接,即可組成液壓齒輪泵的故障特征向量。
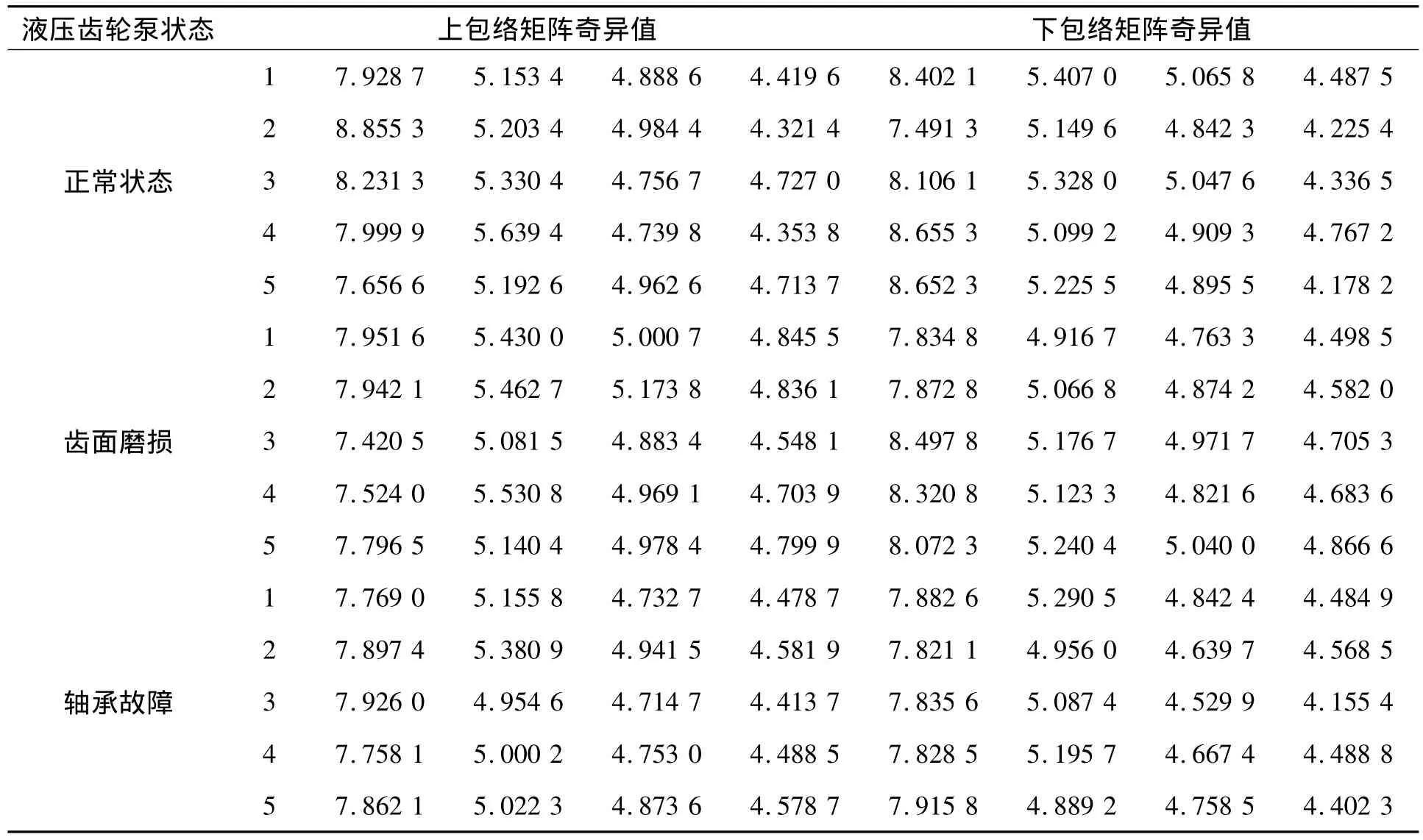
表1 齒輪泵源信號包絡矩陣的奇異值特征向量 (量綱一)
觀察和比較表1中的奇異值數值,可知:由源信號上、下包絡矩陣的奇異值組成的故障特征向量,在液壓齒輪泵的不同故障模式下具有比較大的差異,而在同一種故障模式下,則具有很好的聚類性,數值比較穩定。
在提取的奇異值特征向量的基礎上,利用LS-SVM分類器[15]來識別和診斷CB-Kp63型液壓齒輪泵的故障類型。在本文中,LS-SVM分類器采用Direeted A-cyclic Graph SVM(DAGSVM)[16]模式,如圖 4 所示。
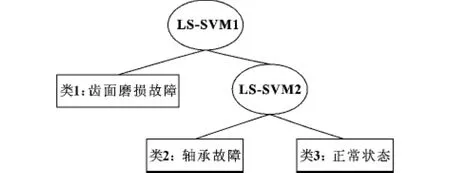
圖4 齒輪泵故障診斷的LS-SVM分類器結構
其中,LS-SVM分類器的核函數取為高斯徑向基函數“RBF_kernel”,它的參數σ=0.2,懲罰因子γ=10。在各個故障模式中,64組樣本隨機分為兩組,其中32組作為訓練樣本,另外的32組作為測試樣本。LS-SVM分類器的測試結果如表2所示。
這里為了進一步比較,也分別將源信號上包絡矩陣的奇異值向量和下包絡矩陣的奇異值向量單獨作為液壓齒輪泵的故障特征向量,并利用LS-SVM分類器進行模式識別和故障診斷。它們的LS-SVM測試結果也列在表2中。
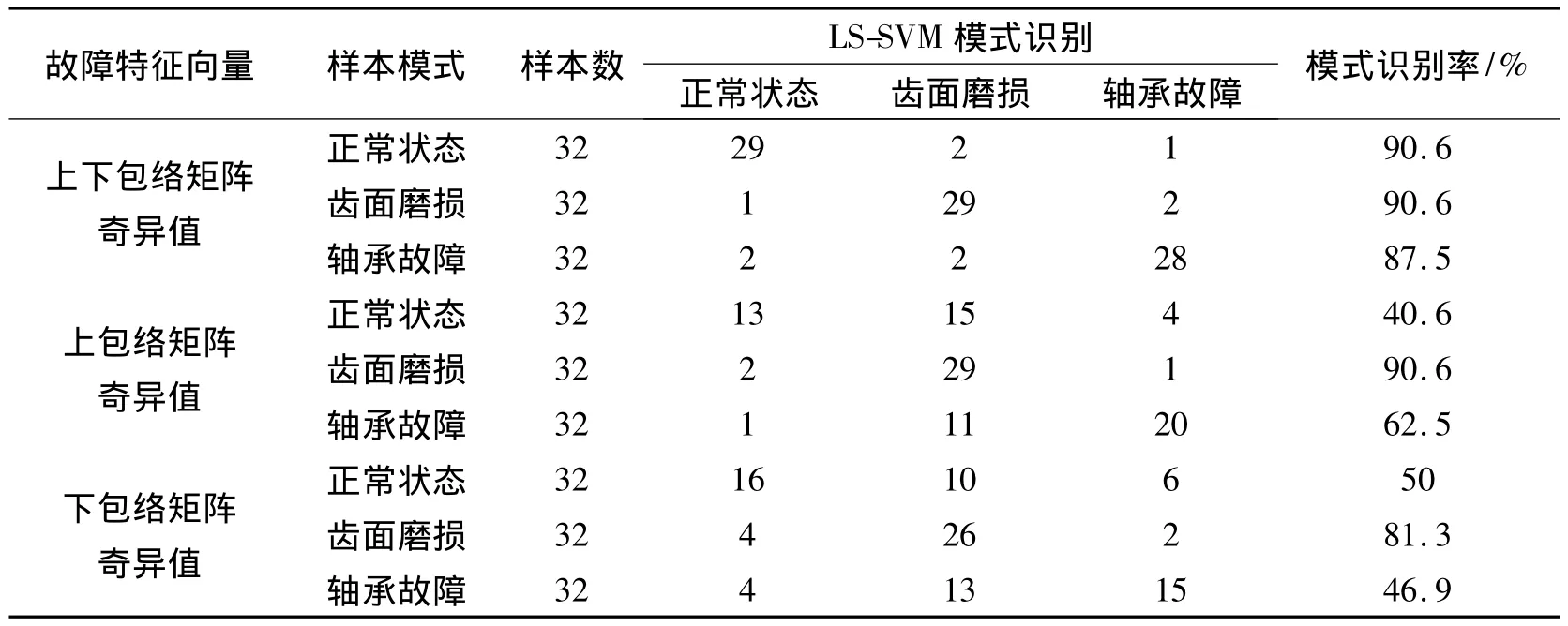
表2 齒輪泵的LS-SVM測試結果
由表2的LS-SVM測試結果可以得知,相比單獨的上包絡矩陣奇異值特征向量或者下包絡矩陣奇異值特征向量,基于源信號上、下包絡矩陣的 (全部)奇異值向量的故障診斷方法的診斷率最高,這表明它是可行的,而且也是準確和有效的,這對于故障源復雜、故障點隱蔽的液壓齒輪泵來說,是一個值得研究和應用的方法。
3 結論
(1)盲源分離可以有效地去除混合信號之間的信息冗余,包絡解調分析可以從高頻調制信號中提取出與故障特征有關的包絡信號,奇異值是矩陣的固有特性,具有比較好的穩定性、比例不變性、旋轉不變性和降維壓縮特性。理論和試驗分析表明,基于源信號包絡矩陣奇異值的故障特征信息具有良好的聚類劃分特性;
(2)最小二乘支持向量機是小樣本模式識別和故障診斷的有效工具,在提取的奇異值特征向量基礎上,它可以有效地識別和診斷機械設備的故障模式;
(3)基于源信號包絡矩陣奇異值的故障診斷方法不僅可以應用于液壓齒輪泵故障診斷,而且它也可以應用于其他的機械設備,具有很好的工程應用價值。
[1]TSE P W,PENG Y H,YAM R.Wavelet Analysis and Envelope Detection for Rolling Element Bearing Fault Diagnosis-their Effectiveness and Flexibilities[J].Journal of Vibration and Acoustics,2001,123(3):303 -310.
[2]SZWOCH G,CZYZEWSKI A,KULESZA M.A low Complexity Double-talk Detector Based on the Signal Envelope[J].Signal Processing,2008,88(11):2856 - 2862.
[3]SHEEN Y T.An Analysis Method for the Vibration Signal With Amplitude Modulation in a Bearing System[J].Journal of Sound and Vibration,2007,303(3 -5):538 -552.
[4]SHEEN Y T.On the Study of Applying Morlet Wavelet to the Hilbert Transform for the Envelope Detection of Bearing Vibrations[J].Mechanical Systems and Signal Processing,2009,23(5):1518 -1527.
[5]SHI D F,WANG W J,QU L S.Defect Detection for Bearings Using Envelope Spectra of Wavelet Transform[J].Journal of Vibration and Acoustics,2004,126(4):567 -573.
[6]GELLE G,COLAS M,SERVIERE C.Blind Source Separation:a New Pre-processing Tool for Rotating Machines Monitoring[J].IEEE Transactions on Instrumentation and Measurement,2003,52(3):790 -795.
[7]SERVIERE C,FABRY P.Blind Source Separation of Noisy Harmonic Signals for Rotating Machine Diagnosis[J].Journal of Sound and Vibration,2004,272(1 -2):317 -339.
[8]ROAN M J,ERLING J G,SIBUL L H.A New non-linear,Adaptive,Blind Source Separation Approach to Gear Tooth Failure Detection and Analysis[J].Mechanical System and Signal Processing,2002,16(5):719-940.
[9]YPMA A,LESHEM A,DUIN R P W.Blind Separation of Rotating Machine Sources:Bilinear Forms and Convolutive Mixtures[J].Neurocomputing,2002,49(1/4):349-368.
[10]TSE P W,ZHANG J Y,WANG X J.Blind Source Separation and Blind Equalization Algorithms for Mechanical Signal Separation and Identification[J].Journal of Vibration and Control,2006,12(4):395-423.
[11]ZHOU W L,CHELIDZE D.Blind Source Separation Based Vibration Mode Identification[J].Mechanical Systems and Signal Processing,2007,21(8):3072-3087.
[12]COMON P.Independent Component Analysis-a New Concept[J].Signal Processing,1994,36(3):287-314.
[13]HYV?RINEN A,KARHUNAEN J,OJA E.Independent Component Analysis[M].New York:John Wiley& Sons,Inc,2001.
[14]FELDMAN M.Analytical Basics of the EMD:Two Harmonics Decomposition[J].Mechanical Systems and Signal Processing,2009,23(7):2059-2071.
[15]SUYKENS J A K,VANDEWALLE J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[16]PLATT J C,CRISTIANINI N,SHAWE J.Large Margin DAGs for Multiclass Classification[J].Advance in Neural Information Processing System,1999,12:547-553.

