基于二進制混沌粒子群算法的認知決策引擎

于 洋，譚學治，殷 聰，張 闖，馬 琳

(哈爾濱工業大學電子與信息工程學院，150080 哈爾濱)

基于二進制混沌粒子群算法的認知決策引擎

于 洋，譚學治，殷 聰，張 闖，馬 琳

(哈爾濱工業大學電子與信息工程學院，150080 哈爾濱)

為了解決不同通信模式下認知無線電發射機參數合理優化的問題，提出了一種基于二進制混沌粒子群算法(BCPSO)的認知決策引擎，該引擎利用粒子群優化算法收斂速度快和混沌運動全局遍歷性的特點，使認知決策在多目標優化過程中有效地擺脫了局部極值點，提高了參數優化的精度和穩定性.基于認知正交頻分復用(OFDM)系統的仿真結果表明，相對于現有認知引擎，該引擎具有平均適應度值高、對不同通信模式魯棒性強的特點，實現了有效優化發射機參數的目的.

認知無線電;認知決策引擎;多目標優化;二進制混沌粒子群算法

為了能夠高效地利用無線電頻譜資源，認知無線電(cognitive radio，CR)技術應運而生［1－2］.美國聯邦通訊委員會(FCC)更確切地把CR定義為基于與操作環境交互的、能動態改變其發射機參數的無線電，其具有環境感知和傳輸參數自我調整的功能.在不同通信模式下，如何合理有效地優化發射機參數以滿足不同服務質量(quality of service，QoS)要求，是認知決策引擎的主要任務.CR通過認知決策引擎制定最優傳輸策略以匹配信道當前狀態，從而實現高效可靠的無線傳輸.

近些年，認知決策引擎的設計問題得到了越來越多的關注［3－10］.認知決策引擎需具備一定的智能性，因此各種人工智能(artificial intelligence，AI)技術被引入到其設計中.因其固有的并行計算能力和良好的可擴展性，遺傳算法(genetic algorithm，GA)被認知決策引擎大量采用［3－6］.模糊邏輯(fuzzy logic，FL)因其可進行模糊綜合判斷，也被應用到認知決策引擎的設計中［7］.為了克服GA早熟等缺點，文獻［8］提出了一種基于二進制粒子群(binary particle swarm optimization，BPSO)算法的認知決策引擎.通過量子理論改進算法，文獻［9］提出了一種基于二進制量子粒子群(binary quantum particle swarm optimization，BQPSO)算法的認知決策引擎.針對認知單載波頻域均衡(singlecarrierfrequencydomain equalization，SC－FDE)系統，文獻［10］提出了一種適用于SC－FDE認知決策引擎的速率控制和自適應調制編碼的聯合算法.本文提出了一種二進制混沌粒子群(binary chaotic particle swarm optimization，BCPSO)算法，并將該算法引入到認知正交頻分復用(orthogonal frequency division multiplexing，OFDM)系統的認知決策引擎中.由于利用了混沌系統的遍歷性，基于BCPSO的認知決策引擎改善了參數優化的精度和魯棒性.

1 粒子群算法

1.1 粒子群算法

粒子群(particle swarm optimization，PSO)算法于1995 年提出［11－12］.因該算法具有收斂速度快、魯棒性好、簡單易于實現等優點，目前已在函數優化、信號處理、模式識別等領域得到了廣泛應用.PSO算法將每個個體視為D維搜索空間中的一個沒有體積和質量的粒子(particle).該粒子具有自學習和社會學習的能力.通過每個粒子對自身速度和位置的逐代更新，最終整個種群在搜索空間中找到全局最優解.

假設某種群中有I個粒子，第i個粒子在D維空間的第k次迭代后速度和位置分別表示為=［，…，］和=［，v，…，v］.粒子的速度和位置更新公式為

式中:w是慣性權重，體現了速度本身的記憶性;c1，c2分別是自學習因子和社會學習因子，為使算法收斂;0 ＜ c1，c2＜ 2;r1，r2是2 個介于［0，1］之間服從均勻分布的隨機數;粒子i在第d維第k次迭代后經歷過的最優位置由表示，整個種群在第d維第k次迭代后經歷過的最優位置為

為了解決離散空間中目標優化的問題，PSO算法的離散二進制形式——BPSO算法被提出［13］.該算法速度更新公式不變，如式(1)所示.但其位置由于被離散化為0或1，相應的更新公式需做以下調整:

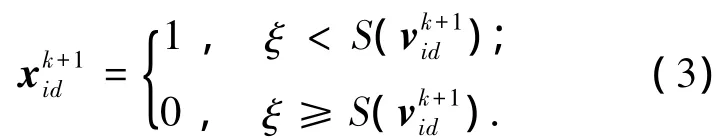
式中:ξ是介于［0，1］之間服從均勻分布的隨機數，S(v)為將連續取值的速度離散化為0或1的Sigmoid函數

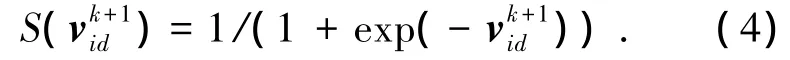
1.2 二進制混沌粒子群算法

本文提出的二進制混沌粒子群算法由于吸收了混沌系統具有的全局遍歷性的優點，因此提高了優化算法的效率.BCPSO算法采用的混沌系統為Logistic方程:

式中:μ為控制參數，m為混沌迭代次數，Z=［z0，z1，…，zm］為混沌序列矢量.若控制參數 μ=4，且初值 z0∈［0，1］，則系統完全處于混沌狀態，且所有混沌變量均介于［0，1］之間.

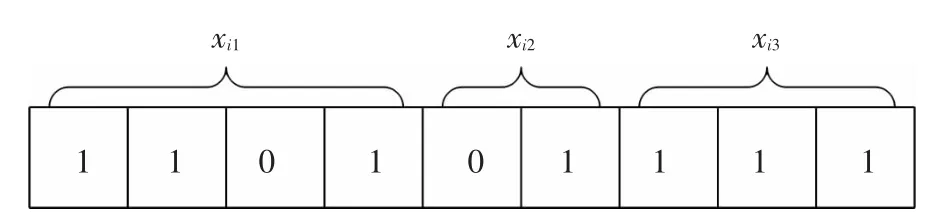
圖1 第i個粒子的二進制編碼

在BCPSO算法中，粒子的維度E應等于可調決策變量的個數.假設存在3個可調決策變量，則粒子的維度為三維.此時，粒子i由3個決策變量xi1，xi2和xi3組合而成，其二進制編碼如圖1所示.若E個決策變量經二進制編碼后其長度分別為li1，li2，…，liE，則搜索空間的維度 D 為

BCPSO算法在混沌優化時，需進行如下的映射和逆映射處理:

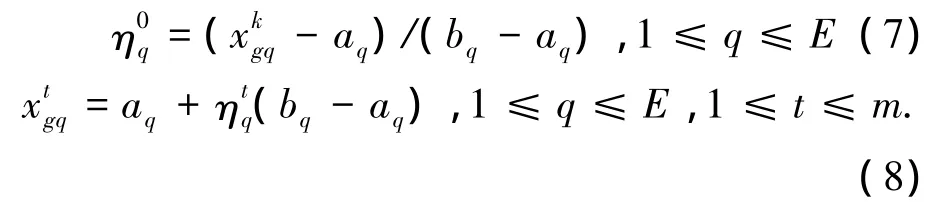
BCPSO算法具體實現流程如下:

1)初始化算法參數和種群.初始化的參數包括最大迭代次數K、慣性權重w、學習因子c1和c2.初始化種群即隨機產生I個粒子的D維位置初矢量=［，，…，x］和 速 度 初 矢 量位置初矢量的每個元素均是0或1.粒子i的最優位置設為

3)根據式(1)和(2)分別對粒子的速度和位置進行更新.對更新后的位置進行二進制譯碼，得到E個決策變量的實數值.計算種群的適應度值，如果粒子 i的適應度值優于 FLbesti，則將此時粒子i的位置設為粒子i的最優位置，同時更新FLbesti;如果此時種群的適應度最大值優于FBest，則該最大值所對應的位置設為全局最優位置同時更新全局最優值FBest.

5)混沌優化.根據式(5)進行混沌迭代，得到混沌矢量序列Ht(1≤t≤m).然后根據式(8)將Ht(1≤ t≤ m)逆映射回 E個決策變量的實數值矢量計算適應度值，同時對其進行二進制編碼，得到原搜索空間的m個矢量若m個矢量的適應度最大值優于FBest，則將全局最優位置］更新為對應于該適應度最大值的矢量，FBest更新為該適應度最大值.用隨機取代當前種群的一個粒子i的位置.

6)判斷是否達到最大迭代次數K:若未達到K，則返回執行3);若達到K，算法結束.

上述算法流程中步驟1)～3)與標準PSO算法相同.但通過步驟4)～5)，BCPSO算法引入了混沌優化過程，該過程改善了原PSO算法跳離局部極值的能力，有效提高了算法精度.

2 基于BCPSO的認知決策引擎

認知決策引擎進行決策的實質可以描述為:利用智能優化算法合理調整可調發射機參數，以達到某種性能組合的最理想實現.即該過程實質上是多目標優化問題.

假設認知無線電中有E個可調決策變量r=ri(i=1，2，3，…，E)和 λ 個目標函數 f=［f1，f2，…，fλ］.任何不同表達形式的多目標函數優化問題都可以轉化成統一的表達形式，且通過將所有目標聚集可把多目標優化問題轉換為單目標問題［14］:

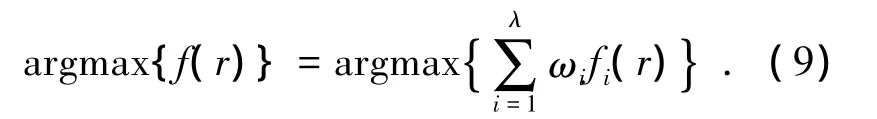
式中ωi，(1≤i≤λ)為介于［0，1］之間的權重系數，且需滿足如下關系:

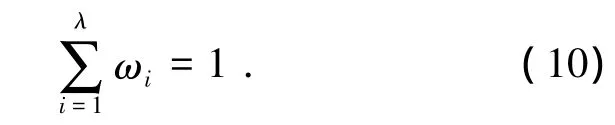
權重系數ωi反映了不同QoS的服務對各目標函數的偏重程度.如當終端處于省電模式下，相應于最小化功率的權重系數ωi就應該設置為最大;再如當用戶在觀看多媒體時，相應于最大化吞吐量的權重系數ωi應該設為最大.可以說，權重系數決定了認知決策引擎的優化方向.因此，認知系統工作模式的切換可以通過調整權重系數加以實現.通過不同權重系數的設置，可以測試并分析在不同通信模式下認知決策引擎的性能.

利用二進制混沌粒子群算法提出的BCPSO算法，可根據式(9)搜索到最優適應度值及其對應的發射機參數組合.我們將該發射機參數組合稱為最優傳輸方案.認知決策引擎決策出最優傳輸方案，并將該方案傳遞給認知系統硬件加以實施.

3 仿真結果與分析

本文的仿真結果均是基于認知OFDM系統得到的.該仿真系統的具體參數如表1所示.該系統發射功率值共有64個，二進制編碼后由6個比特組成;調制方式4種，由2個比特組成.這樣一個子載波由8比特組成，32個子載波共計有256個比特.即粒子維度D=256.

表1 認知OFDM系統參數

每個子載波有2個決策變量:調制方式和功率.這樣32個子載波共有64個決策變量，即E=64.背景噪聲為加性高斯白噪聲，噪聲功率－60 dbm，路徑損耗60 dB.假設仿真系統的目標函數分別為最小化發射功率、最小化誤碼率(bit error rate，BER)和最大化吞吐量.各目標函數歸一化表達式為

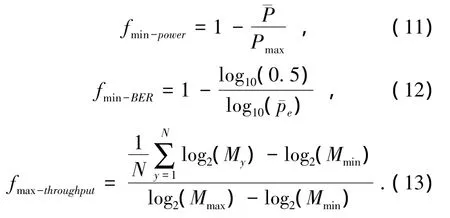
將式(11)～(13)表示的目標函數聚集為如下單目標函數:

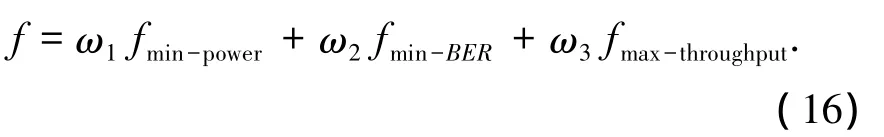
式中f即為適應度函數，其反映了系統對發射功率、誤碼率和吞吐量的綜合需求，用以評價發射參數優化配置的好壞.

假設認知OFDM系統工作在以下3種模式:低功耗模式、緊急模式和多媒體模式.3種通信模式相應的權重系數如表2所示.在表2的低功耗模式下，系統對發射功率的要求較高，為此，反映功率的子目標函數fmin-power的權重系數ω1被設為最大，為0.8;同理，緊急模式和多媒體模式分別對反映誤碼率的子目標函數fmin-BER的權重系數ω2和反映吞吐量的子目標函數fmax-throughput的權重系數ω3設為最大.

文中提出的BCPSO算法的具體參數如表3所示.為了進行性能對比，文中也對分別基于GA［3］、BPSO 算法［8］和 BQPSO 算法［9］的認知引擎進行了仿真.其中GA采用輪盤賭選擇，單點交叉，交叉概率為0.6，變異概率為0.001.而BPSO算法和BQPSO算法的參數與表3所示的前7列一致.

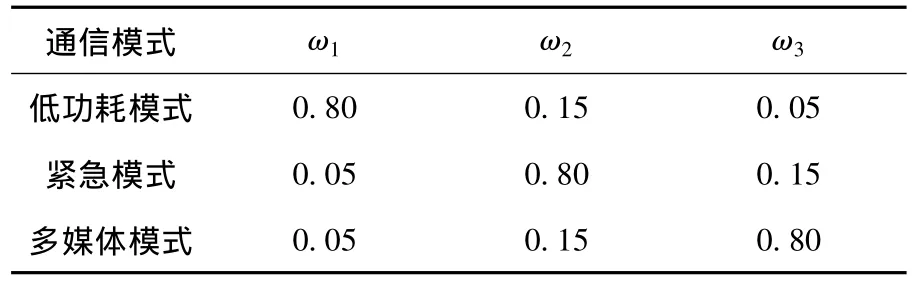
表2 3種通信模式的權重系數

表3中粒子維度D的取值與決策變量個數及取值個數有關，慣性權重w、自學習因子c1、社會學習因子c2的選取均為PSO算法的經典取值，混沌控制參數μ取值為4可以保證混沌系統完全處于混沌狀態.種群大小I、最大迭代次數K和混沌最大迭代次數m其取值與具體系統要求有關.若系統對實時性要求很高，則上述3個參數應取較小值;反之，當系統對實時性不敏感，而對適應度性能要求較高時，則上述參數可取較大值以保證性能要求.對仿真系統的實時性和性能要求進行折中，從而確定表3中種群大小I、最大迭代次數K和混沌最大迭代次數m的相應取值.粒子速度最大值Vmax=4為仿真經驗值.另外，最大迭代次數K的選取需要通信的雙方相互反饋確定.離線狀態下進行系統仿真，可得到一次迭代的時間代價，認知無線電系統將這一參數存儲到CR知識庫中.在線狀態時，認知系統通過信道認知引擎感知到當前信道的信道相干時間等狀態信息，并將該信息傳遞給認知決策引擎.認知決策引擎根據獲得的信道相干時間和CR知識庫提供的一次迭代的時間代價，據此確定最大迭代次數K的取值.由于信道認知引擎和CR知識庫超出了文中研究范疇，相關具體內容可參見文獻［16］.

表3 BCPSO算法參數

表4給出了在3種通信模式下，通過基于BCPSO的認知決策引擎優化后的平均發射機參數.如表4所示，在低功耗模式下，認知決策引擎通過減小平均發射功率的方式以保證用戶功耗達到最低.在緊急模式下，為了保證系統的高可靠性傳輸，需使系統平均BER達到最小.為此，認知決策引擎通過提高發射功率和降低調制階數的方式加以實現.在多媒體模式下，為使系統平均吞吐量達到最大，認知決策引擎使平均調制階數達到最大.由此可見，通過改變目標函數中的權重系數，文中提出的認知決策引擎可以沿著不同的方向進行優化，以保證不同通信模式不同QoS服務的實際需求.

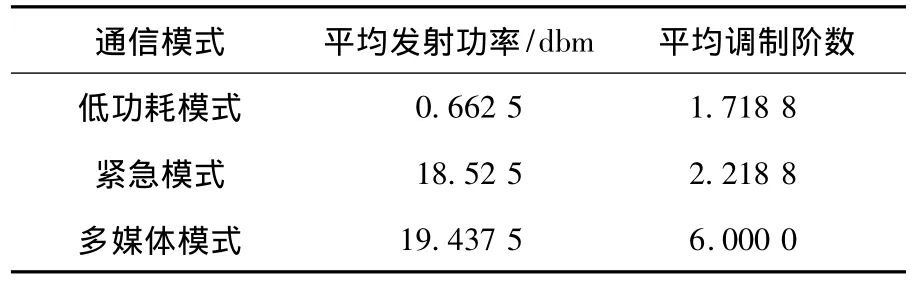
表4 3種通信模式下的BCPSO的平均發射機參數

圖2～4分別給出了低功耗模式、緊急模式和多媒體模式下4種算法的平均歸一化適應度值性能曲線.在上述 3種通信模式下，每種算法經1 000次迭代后的平均適應度值如表5所示.不同算法的收斂性能如表6所示.

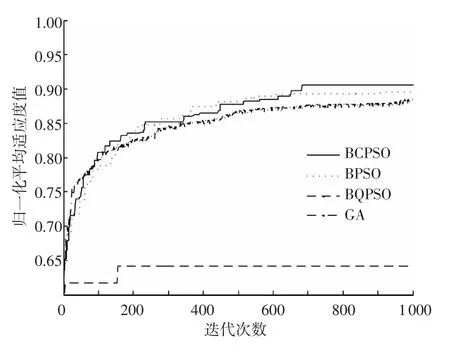
圖2 低功耗模式下性能對比

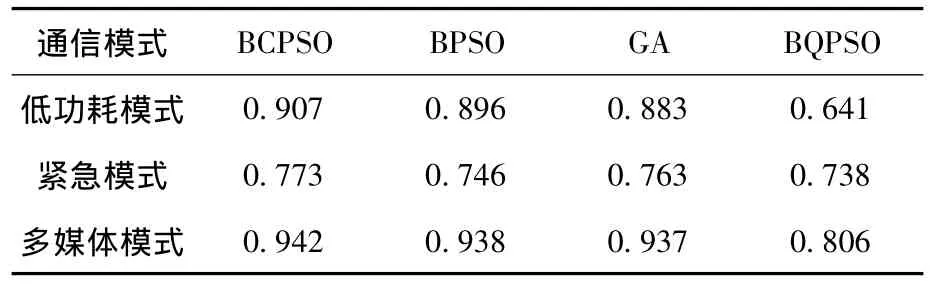
表5 3種通信模式下的平均適應度值

如圖2和表5所示，低功耗模式下，在算法精度方面，提出BCPSO算法最好，以下依次為BPSO算法、GA和BQPSO算法.BCPSO算法的平均適應度值為0.907，高過次優的BPSO算法 0.011.如圖2和表6所示，在收斂性方面，BQPSO算法在155次迭代后即收斂，但由于其適應度值較差，可以看出BQPSO算法出現了“早熟”現象.除了BQPSO算法，文中提出的BCPSO算法的收斂速度明顯比GA和BPSO算法更快.

如圖 3和表 5所示，緊急模式下，提出BCPSO算法在精度方面有顯著優勢.此時該算法的平均適應度值為0.773，高過次優的GA 0.01.如圖3和表6所示，除“早熟”的BQPSO算法外，BPSO算法收斂最快，其次BCPSO算法，最差的是GA.BCPSO算法精度性能的優勢是以犧牲部分收斂性能為代價的.

表6 3種通信模式下的收斂性能

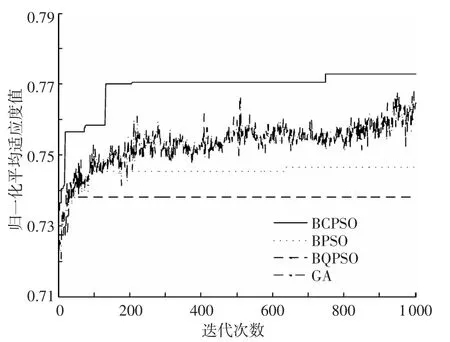
圖3 緊急模式下性能對比

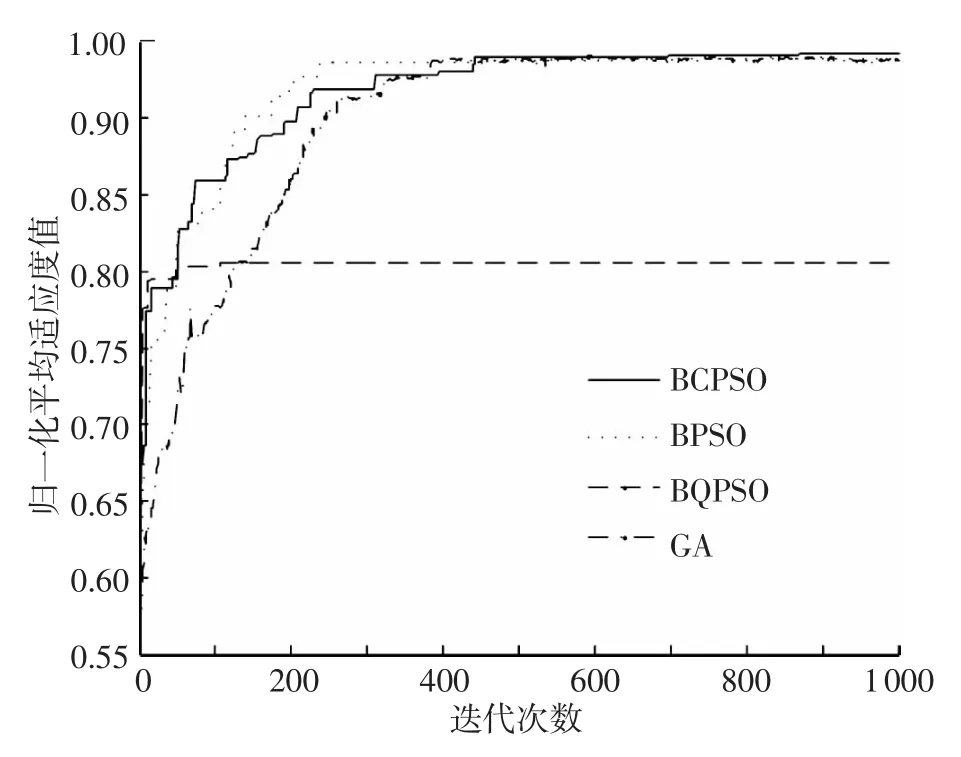
圖4 多媒體模式下性能對比

如圖4和表5所示，在多媒體模式下，在算法精度方面，提出 BCPSO算法最好，以下依次為BPSO算法、GA和BQPSO算法.但前3者的平均適應度值非常接近.如圖4和表6所示，不考慮“早熟”的BQPSO算法，文中提出的BCPSO算法收斂性能不如GA和BPSO算法.

綜合上述分析，在3種不同通信模式下，雖然文中提出的BCPSO算法有時收斂性能不是最好，但其以犧牲部分收斂性能為代價，換來了精度的提高.此外，3種通信模式下，該算法的精度性能始終保持最高，也體現了算法自身較強的魯棒性.這表明文中提出的BCPSO算法和基于該算法的認知決策引擎能夠保證認知OFDM系統在不同通信模式下高效可靠地自適應傳輸.

4 結語

本文首先提出了一種新型智能優化算法，稱為BCPSO算法.在此基礎上，提出了基于BCPSO的認知決策引擎.該引擎吸收了混沌理論的全局遍歷性，使其在多目標優化過程中擺脫了局部極值的不利影響，有效提高了優化性能.由基于認知OFDM系統的仿真結果可以看出，本文提出的認知決策引擎能夠高效地對發射機參數進行優化配置.其優化的適應度值更高，且針對不同通信模式其魯棒性也更好.這表明本文提出的認知決策引擎能夠滿足認知系統對發射機參數合理優化的需求.

［1］MITOLA J，MAGUIRE G.Cognitive radio:making software radios more personal［J］.IEEE Personal Communications Magazine，1999，6(4):13－18.

［2］MITOLA J. Cognitive radio forflexible mobile multimedia communications［C］//Proceedings of IEEE International Workshop on Mobile Multimedia Communications’99.San Diego:IEEE，1999:3－10.

［3］RIESER C J.Biologically inspired cognitive radio engine model utilizing distributed genetic algorithm for secure and robust wireless communications and networking［D］.Blacksburg:Virginia Polytechnic Institute and State University，2004:35－57.

［4］RIESER C J，RONDEAU T W，BOSTIAN C W，et al.Cognitive radio testbed:further details and testing of distributed genetic algorithm based cognitive engine for programmable radios［C］//Proceedings ofIEEE Military Communication Conference.Monterey:IEEE，2004:1437－1443.

［5］AYMAN A E，MAHAMOD I，MOHD A M A，et al.Development of a cognitive radio decision engine using multi-objective hybrid genetic algorithm ［C］//Proceedings of the 2009 IEEE 9th Malaysia International Conference on Communications.Kuala Lumpur:IEEE，2009:343－347.

［6］WU Di，WANG Feng，YANG Shengyao.Cognitive radio decision engine based on priori knowledge［C］//Proceedings of the 3rd International Symposium on Parallel Architecture， Algorithm and Programming.Dalian:Conference Publishing Services(CPS)，2010:255－259.

［7］KHEDR M，SHATILA H.A cognitive radio approach for WiMAX systems［C］//Proceedings of the 7th IEEE/ACS InternationalConference on Computer Systems and Applications.Rabat:IEEE，2009:550－554.

［8］趙知勁，徐世宇，鄭仕鏈，等.基于二進制粒子群算法的認知無線電決策引擎［J］.物理學報，2009，58(7):5118－5125.

［9］張靜，周正，高萬鑫，等.基于二進制量子粒子群算法的認知無線電決策引擎［J］.儀器儀表學報，2011，32(2):451－456.

［10］YU Yang，TAN Xuezhi，CHI Yonggang，et al.A joint rate control and AMC algorithm for adaptive transmission systems［J］.Journal of Harbin Institute of Technology(New Series)，2013，20(2):12－16.

［11］EBERHART R，KENNEDY J.A new optimizer using particle swarm theory［C］//Proceedings of the 6th IEEE International Symposium on Micro Machine and Human Science.Piscataway:IEEE，1995:39－43.

［12］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE，1995:1942－1948.

［13］KENNEDY J，EBERHART R.A discrete binary version ofthe particle swarm algorithm ［C］//ProceedingsofIEEE InternationalConference on Computational Cybernetics and Simulation.Orlando:IEEE，1997:4104－4108.

［14］鄭金華.多目標進化算法及其應用［M］.北京:科學出版社，2007:2－10.

［15］GOLDSMITH A. WirelessCommunications［M］.Cambridge:Cambridge University Press，2005:130 －131.

［16］于洋，譚學治.基于信道分類和自適應調制編碼的認知無線電決策引擎［J］.電子與信息學報，2014，36(2):371－376.

Cognitive decision engine based on binary chaotic particle swarm optimization

YU Yang，TAN Xuezhi，YIN Cong，ZHANG Chuang，MA Lin
(School of Electronics and Information Engineering，Harbin Institute of Technology，150080 Harbin，China)

To solve the problem of transmitter parameter optimization in different communication modes for cognitive radio(CR)systems，a cognitive decision engine based on binary chaotic particle swarm optimization(BCPSO)is proposed.The BCPSO algorithm has both the fast convergence of particle swarm optimization and global ergodic property of chaos.Therefore，the cognitive decision engine based on BCPSO can jump off the local extreme points effectively，which can improve the precision and stability of parameter optimization.The cognitive orthogonal frequency division multiplexing(OFDM)system is used for the performance analysis.And the simulation results show that the proposed cognitive decision engine，which has higher fitness value and stronger robustness for different communication modes，is better than the other existing engines.The proposed engine achieves the objective of parameter optimization effectively.

cognitive radio;cognitive decision engine;multi-objective optimization;binary chaotic particle swarm optimization

TN914.3

A

0367－6234(2014)03－0008－06

2013－07－08.

國家自然科學基金委員會與中國民用航空局聯合資助項目(61071104);國家科技重大專項“寬帶多媒體集群系統技術驗證(中速模式)”(2011ZX03004－004).

于 洋(1984—)，男，博士研究生;

譚學治(1957—)，男，教授，博士生導師.

譚學治，tanxuezhi－hit@163.com.

(編輯 苗秀芝)