高溫高壓條件下堆積顆粒的吸能效應

王宏亮， 田 宙， 郭永輝

（西北核技術研究所，陜西西安 710024）

高溫高壓條件下堆積顆粒的吸能效應

王宏亮， 田 宙， 郭永輝

（西北核技術研究所，陜西西安 710024）

建立二維軸對稱氣固兩相雙流體物理模型.對三種不同源區初始質量比內能E0／10、E0／100、E0／1 000，固體堆積顆粒作用下氣相流場能量、壓力衰減進行數值模擬.結果表明：初始質量比內能越高，堆積顆粒作用下流場動能、內能衰減越快；初始質量比內能越高，流場壓力衰減達到準靜狀態的速度越快，準靜態后壓力衰減也越快.

高溫高壓；雙流體模型；有限體積方法；堆積顆粒；能量衰減

0 引言

爆炸實驗中，在激波傳播路徑上，適時噴灑粉塵抑爆劑，或提前設置堆積顆粒，可達到衰減激波，抑制爆炸的目的［1－8］.目前，關于粉塵或堆積顆粒抑爆問題所開展的實驗和數值研究中，重點關注的基本是堆積顆粒或懸浮粒子的動力學行為對沖擊波載荷的影響，而未對高溫條件下，堆積顆粒吸熱效應對于流場能量及沖擊波載荷的影響進行細致研究.

高溫高壓環境下，氣相流場與固相顆粒通過熱傳導、輻射傳熱機制進行熱量傳遞，當固相顆粒溫度達到熔點、沸點時發生相變，從而可能向氣相流場傳遞質量.理論上，單位時間內球形顆粒表面通過對流換熱同周圍流體之間的傳遞的熱量同兩者的溫差成正比，而以輻射方式彼此傳遞的熱量同兩者溫度四次方的差成正比，這里固相溫度指其表面溫度，溫度越高，熱量傳遞效率越高，輻射傳熱較對流傳熱的影響也會越來越重要，會對流場沖擊波載荷造成影響.

利用高溫高壓多相流體動力學已有研究成果，建立二維軸對稱氣固兩相雙流體物理模型，并設計高效非結構有限體積數值計算方法對模型進行數值求解，用所建立的方法成功對具體實驗條件下沙墻消波吸能效應進行數值研究，計算結果表明：沖擊波到時、容器內準靜氣壓數值計算結果同實驗結果符合良好，驗證了所建物理模型及計算方法解決高溫高壓條件下堆積顆粒吸能物理問題的合理性［9］.應用上述數值算法，設定不同等溫等壓源區條件，對顆粒吸能效應進行數值模擬，對比分析不同初始質量比內能條件下，氣相能量衰減以及流場壓力時間歷程.結果表明：源區相同能量、壓力，不同質量條件下，溫度不同時，堆積顆粒作用下流場能量衰減速率、沖擊波載荷衰減速率存在很大的差異，氣固熱交換是影響流場壓力變化的重要因素，且源區初始質量比內能越小，影響越突出.

1 物理模型

高溫高壓條件下，氣流同堆積顆粒的相互作用機理為：一方面，堆積顆粒在激波作用下快速飛散，導致部分流場能量轉變為顆粒動能；另一方面，顆粒在高溫氣流沖刷下升溫，可能熔化、汽化，部分流場能量轉變為顆粒內能；此外，顆粒在高速氣流沖擊下可能破碎細化，消耗部分流場能量，細化顆粒會進一步吸收流場能量.

基于連續介質假設，將稠密堆積顆粒當作連續相在Euler坐標系中處理，考慮相間雙向耦合作用，基于合理簡化，推導氣相－固相控制方程.

1.1 基本假定

物理模型基本假定如下：

①不考慮空氣粘性；

②不考慮固相粘性，考慮固相分壓，固相本構方程基于彈性體假設推導得到；

③考慮氣體－顆粒間通過熱傳導、輻射傳熱機制所引起的熱量傳遞；

④考慮顆粒受熱相變，及汽化引起的質量傳遞，但假設顆粒為惰性物質，不發生化學反應，圖1為顆粒比內能同溫度的關系，圖中：Qmelt、Qeva代表顆粒熔化熱、汽化熱.

⑤考慮氣體－顆粒間由于速度差，通過阻力作用所引起的動量傳遞，不考慮顆粒所受重力等；

⑥固相顆粒粒徑均勻一致，不考慮粒子破碎過程，固相顆粒粒子數保持不變.

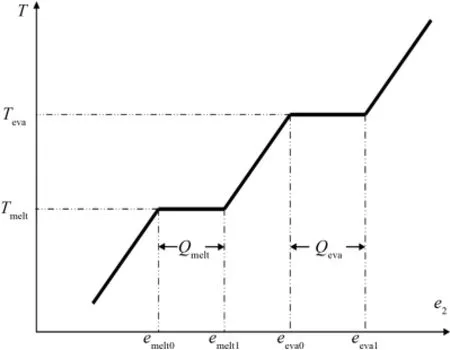
圖1 顆粒比內能同溫度的關系Fig.1 Specific internal energy of a particle as function of temperature

1.2 控制方程

基于以上假定，氣固兩相Euler-Euler型二維軸對稱控制方程組，

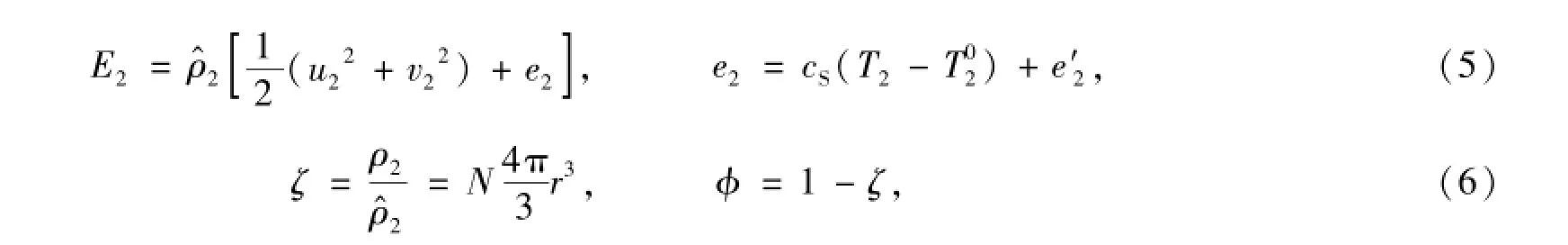
式中，氣相、固相控制方程中第一式為質量守恒方程，第二、第三式為動量守恒方程，第四式為能量守恒方程，固相控制方程最后一式為粒子數守恒方程；F代表氣相、固相質量、動量、能量、粒子數守恒量矢量；G、H代表氣固質量、動量、能量、粒子數沿軸向、徑向單位面積對流通量矢量；Ψ代表氣固方程右端源項；φ、ρ1、u1、v1、e1、E1、T1、p1分別代表氣相單元體積分數、密度、徑向速度、法向速度、單位質量比內能、單元總能量、溫度、壓力；γ代表氣相絕熱指數；ζ、ρ＾2、u2、v2、e2、E2、T2、p2、N分別代表固相單元體積分數、顆粒材料密度、徑向速度、法向速度、單位質量比內能、單位體積總能量、溫度、壓力、單位體積粒子數目；r、cS代表粒子半徑、比熱容.

對于固相壓力，其表達式稱為固相本構方程，是為了描述顆粒碰撞所引起的固相應力，由于不考慮固相粘性，即不考慮固相切應力，僅考慮固相法向應力.關于固相粘度、應力問題，國內外學者提出不同描述方法，如Pritchett（1978）和Lyczkowski（1993）等采用固體彈性模量模型、Ding＆Gidaspow（1990）等所提出的分子動力學模型，以及范寶春等根據激波與堆積粉塵相互作用的實驗結果以及斜激波的相關理論所確定的堆積粉塵本構方程等［9］.本文通過彈性體假設提出堆積顆粒本構方程，

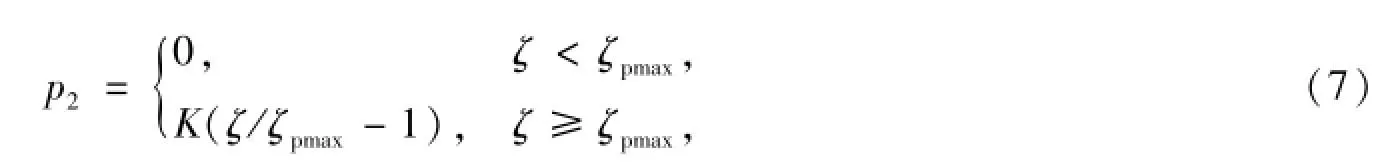
式中：K為顆粒材料體積模量；ζ為顆粒堆積體積分數；ζpmax為球形顆粒的最大堆積密度，在實際應用中需參考實驗結果進行修正，具體推導過程參見文獻［10］.

控制方程右端，除第一項，其余各項分別代表兩相質量、動量、熱量交換作用，其計算公式如下：

采用Sreznevsky液滴蒸發模型描述氣相、固相之間的質量交換式（8），假設固相顆粒為惰性粒子，當其溫度達到沸點時，發生汽化，從而向氣相流場傳遞質量.

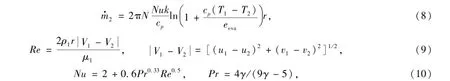
式中：k代表氣體熱傳導系數；Nu為Nusselt數，Pr為Prandtl數；Re代表Reynolds數；μ1、cp代表氣相介質粘性系數及定壓比熱容.

采用牛頓阻力定律描述高雷諾數條件下氣固兩相之間的阻力作用式（11）、式（12），阻力系數計算公式見式（13）.

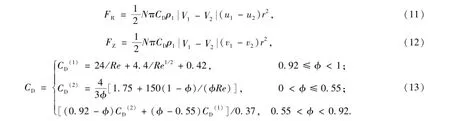
式中：CD為阻力（驅動力）系數；FR、FZ分別為兩相介質之間徑向、軸向動量交換有關的驅動力項.氣固兩相之間的熱量交換率，

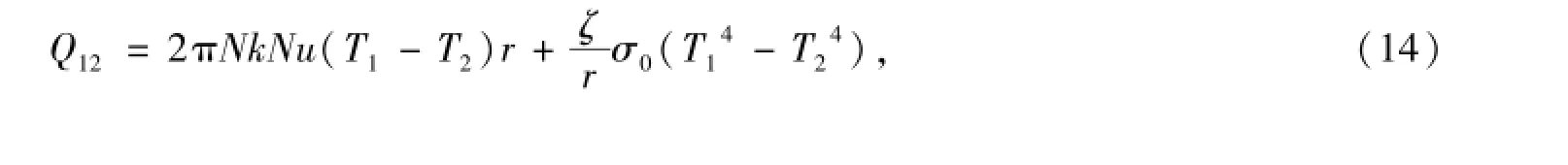
式中，右端第一、第二項分別代表熱傳導、輻射傳熱所引起的熱量傳遞；σ0為斯蒂芬－玻爾茲曼常數，其值為5.67×10－8J·（s·m2·K4）－1.

2 堆積顆粒吸能效應

數值研究源區初始體積比內能、壓力相同，初始質量、溫度不同時，見表1，堆積顆粒作用下流場能量、壓力變化規律.

表1 計算條件Table 1 Computational conditions

2.1 計算條件

計算模型如圖2所示，約束空間區域半長為20 m，半徑1.0 m，堆積顆粒位置如圖所示.堆積顆粒為沙粒，初始堆積體積分數約為0.4，沙粒物性條件見表2.計算中，氣相為單一空氣介質，初始時刻，流場源區處于高溫高壓狀態，源區以外區域氣體處于標準狀態.

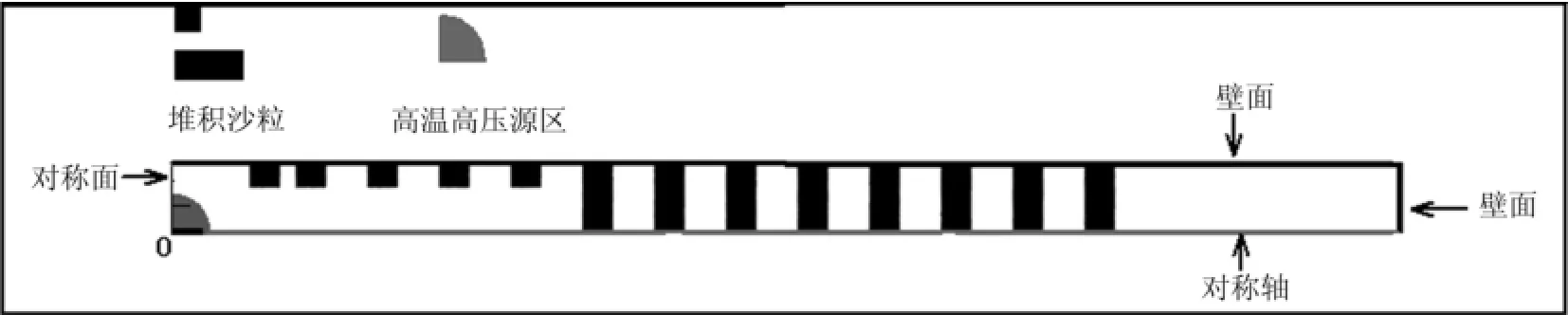
圖2 計算模型Fig.2 Computational model

表2 沙粒物性條件Table 2 Physical and thermodynamical parameters of sand particles

2.2 計算結果

根據以往研究，沖擊波與堆積顆粒相互作用過程中，堆積顆粒，一方面在沖擊作用下發生擠壓，透射波過后，堆積顆粒自自由表面層層發生飛散運動；另一方面，在波后氣流作用下，其速度、溫度會不斷增大.而沖擊波在堆積顆粒作用下，會發生反射、透射、繞射等物理現象.因此，在沖擊波與堆積顆粒相互作用過程中，沖擊波對堆積顆粒做功，其載荷降低，傳播速度降低，即流場動能向堆積顆粒進行了轉移；另外，由于波后氣流與堆積顆粒之間仍然存在速度差、溫差，因此在作用過程中，流場動能、內能會不斷向堆積顆粒進行轉移，從而造成流場總能量衰減.

圖3為t＝0.05 ms時刻，三種計算條件下，流場壓力等值云圖，如圖所示：源區初始能量、體積相等時，源區質量越小，源區膨脹所產生首道沖擊波傳播速度越快，當然波后介質速度也更快.圖4為t＝1.0 ms時刻，三種計算條件下，流場壓力等值云圖，從圖中可以看出：沖擊波在堆積顆粒作用下，發生明顯繞射現象.

圖5、圖6、圖7為三種計算條件下，氣相總能量、總動能、總內能隨時間變化，顯然：源區初始體積比內能相等時，源區質量越小，氣相總能量、總動能、總內能衰減越快；源區初始體積比內能相等時，源區質量越大，源區總能量轉化為氣相動能的比例越大，但三種情況下，氣相以動能形式衰減的能量不超過氣相總能量的20%，大部分能量將以熱能的形式被顆粒吸收.源區質量等于10 kg、100 kg、1 000 kg時，氣相總能量趨于平衡的時刻分別為1 ms、幾十ms、百ms.從圖中可以看出，氣相總能量與總內能變化趨勢一致，氣相總內能趨勢變化，決定流場達準靜態后壓力衰減趨勢.也就說明，源區初始體積比內能相同時，質量越小，沖擊波載荷衰減達準靜態后壓力衰減速率越快.圖8、圖9為三種計算條件下，約束空間壁面Z＝0.0 m、6.21 m處，壓力隨時間變化曲線，如圖所示：質量越小，沖擊波脈寬越窄，傳播速度越快，激波衰減速率也越快，即：流場內能衰減對于激波衰減的影響也越大.

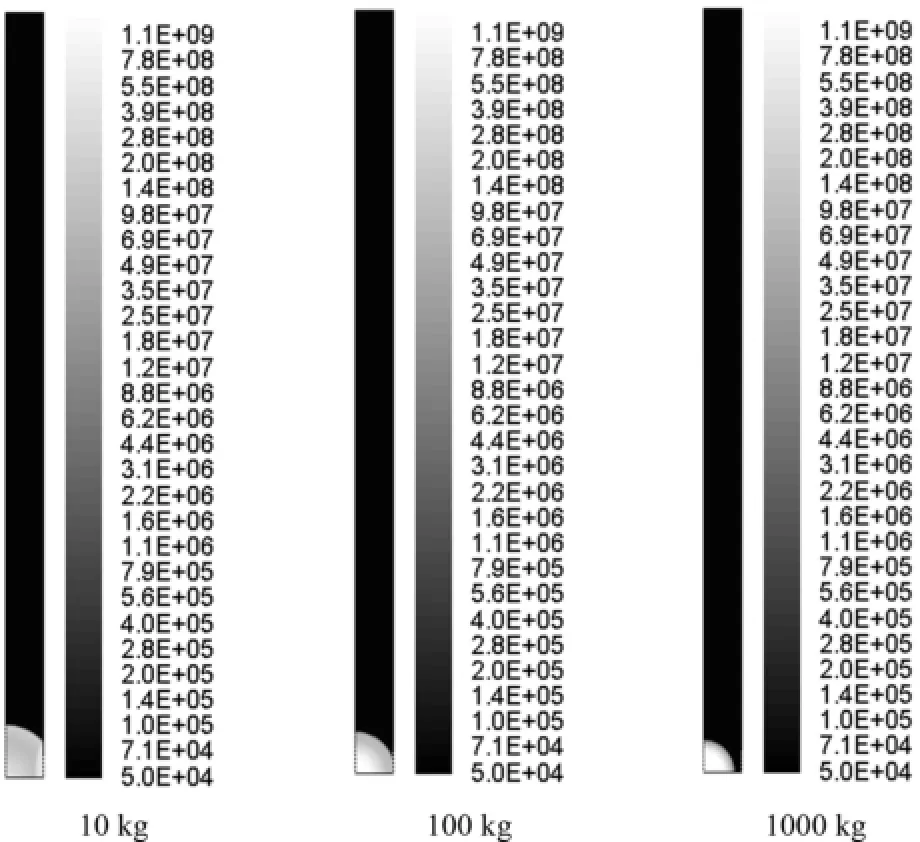
圖3 三種計算條件下，t＝0.05 ms時刻，壓力云圖Fig.3 Pressure contours at t＝0.05 ms under conditions in Table 1

圖4 三種計算條件下，t＝1.0 ms時刻，壓力云圖Fig.4 Pressure contours at t＝1.0 ms under conditions in Table 1

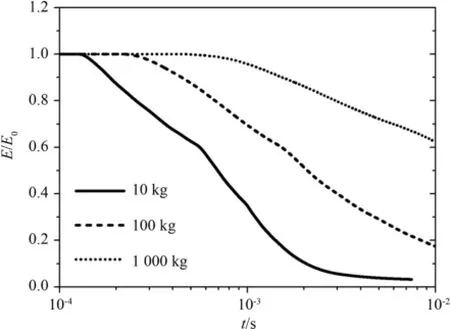
圖5 三種計算條件下，氣相總能量隨時間變化Fig.5 Ratio of gas total energy to E0 under conditions in Table 1

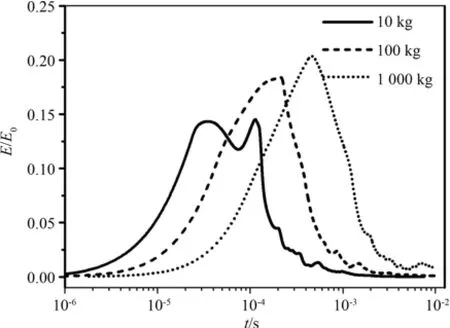
圖6 三種計算條件下，氣相動能隨時間變化Fig.6 Ratio of gas kinetic energy to E0 under conditions in Table 1

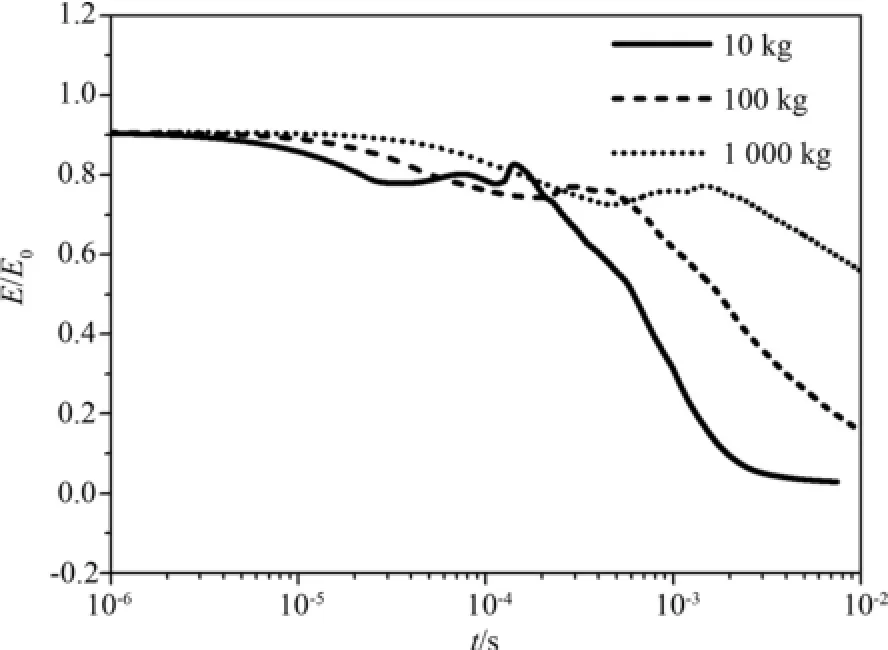
圖7 三種計算條件下，氣相內能隨時間變化Fig.7 Ratio of gas internal energy to E0 under conditions in Table 1

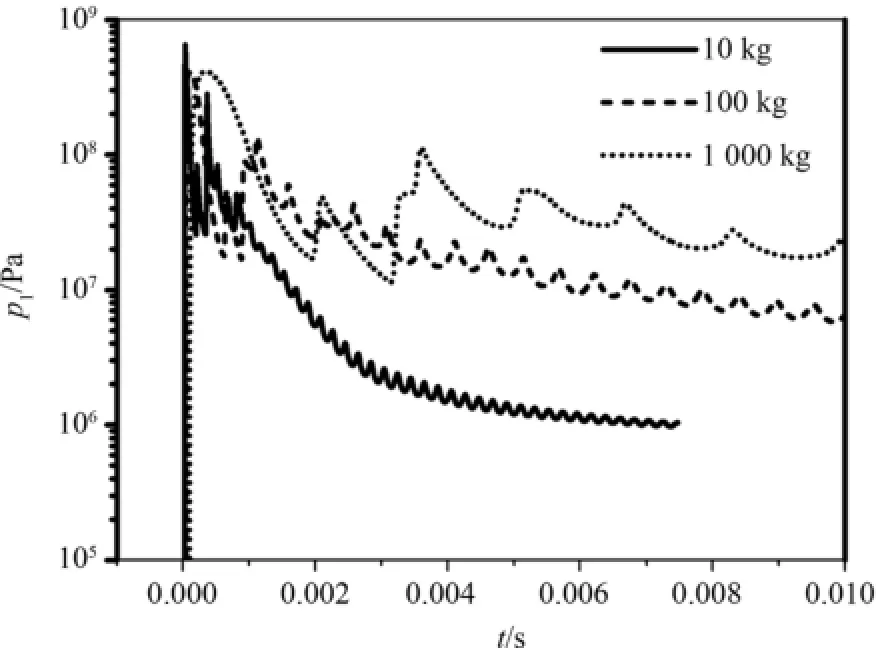
圖8 三種計算條件下，約束空間壁面z＝0.0 m處壓力隨時間變化Fig.8 Pressure vs.time at z＝0.0 m on wall of computational model under conditions in Table 1

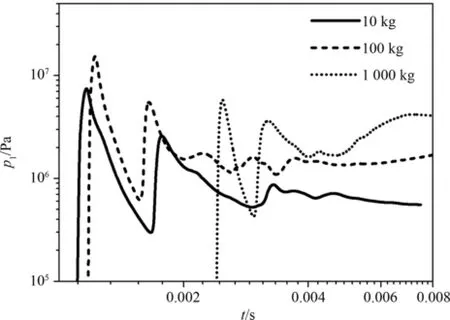
圖9 三種計算條件下，約束空間壁面z＝6.21 m處壓力隨時間變化Fig.9 Pressure vs.time at z＝1.0 m on wall of computational model under conditions in Table 1

3 結論

通過上述研究，當三種源區條件能量相同、體積相同，氣相采用一種狀態方程描述，壓力相同，可以得到以下結論：

1）不超過20%源區能量以動能形式發生衰減，即大量源區能量將以熱能形式發生衰減；

2）氣相動能衰減速率，決定了流場達準靜態的時刻.氣相流場初始質量比內能越高，沖擊波脈寬窄，傳播速度快，造成固相顆粒作用下氣相動能衰減越快，流場達到準靜態越快.

3）氣相內能衰減速率，決定了流場達準靜態后壓力衰減的快慢.初始質量比內能越高，氣相總內能衰減越快，流場達準靜態后壓力衰減也越快.也就表明：氣固兩相之間熱量交換，對于流場壓力變化具有重要影響，且初始質量比內能越高，這種影響越顯著.

［1］ Fan Baochun，Xie Bo，Zhang Xiaohe，et al.Experimental research on explosion suppression by inert particles［J］. Experiments and Measurements in Fluid Mechanics，2001，15（4）：20－25.

［2］ Fan Baochun，Li Hongzhi.Numerical simulations of explosion suppression by inert particles［J］.Explosion and Shock Waves，2000，20（3）：208－214.

［3］ Xie Bo，Fan Baochun.Study on active explosion suppression by powder in large-scale duct［J］.Chinese Journal of Applied Mechanics，2010，27（2）：280－286.

［4］ Zhang Lite，Shi Honghui.Reflection and transmission mechanism of shock wave interacting with moveable particle group［J］. Journal of China Coal Society，2010，27（2）：280－286.

［5］ Zhang Dezhi，Zhong Fangping，Ma Yanjun，et al.Experimental investigation on explode loading of the slender cylindrical vessel［C］.8th Symposium on Shock＆Impact Dynamics Yinchuan，China，2007.

［6］ Cui Yunxiao，Hu Yongle，Chen Jianjie，et al.Numerical simulation for explosive test in explosion containment vessel filled with sand［C］.9th Symposium on Shock＆Impact Dynamics，Jiaozuo，China，2009.

［7］ Yu Yong，Zhang Xia，Chen Wei.Simulation of supersonic gas-particle two-phase flow with two-fluid model［J］.Journal of Aerospace Power，2010，25（4）：800－807.

［8］ Lei Ming，Zhang Baihua，Wang Hongliang，et al.Numerical simulation of effect of energy absorption of sand walls under blast wave［J］.Journal of PLA University of Science and Technology，2007，8（5）：434－438.

［9］ Wang Hongliang，Tian Zhou，Guo Yonghui.Numerical study of effect of sand-walls on shock wave attenuation［C］.1st National Conference on Explosion Vessel，Sichuan，China，2010.

［10］ Wang Hongliang，Tian Zhou.Deduction of constitutive equation of granular materials based on plastic theory［C］.Advances in Computational Explosion Mechanics，Qingdao，China，2006.

Effect of Particles-piled on Energy Attenuation at High Temperature and High Pressure

WANG Hongliang， TIAN Zhou， GUO Yonghui
（Northwest Institute of Nuclear Technology，Xi'an 710024，China）

Two-dimensional axi-symmetric gas-solid two-fluid model was established.Under three conditions of source：E0／10，E0／100，E0／1 000（initial energy per mass of gas），diminishing of gas energy and gas pressure caused by packing particles was studied.It shows that：With higher initial energy per mass of source kinetic and internal energy of gas is diminished by packing particles more quickly，gas fluid is close to stillness more quickly，gas pressure is decreased more quickly.

high temperature and high pressure；two-fluid model；packing particles；energy attenuation

date： 2013－11－26；Revised date： 2014－04－25

O359

A

2013－11－26；

2014－04－25

王宏亮（1983－），女，碩士，主要從事兩相流研究，E-mail：wanghongliang＠nint.ac.cn

1001-246X（2014）06-0706-07