快速反演算法在汽輪機蒸汽濕度測量中的應用

劉芳艷，黃竹青，2*，曹小玲，蔡 成，楊 穎

（1.長沙理工大學能源與動力工程學院，長沙410114；2.湖南有色金屬職業技術學院，株洲412006）

快速反演算法在汽輪機蒸汽濕度測量中的應用

劉芳艷1，黃竹青1，2*，曹小玲1，蔡 成1，楊 穎1

（1.長沙理工大學能源與動力工程學院，長沙410114；2.湖南有色金屬職業技術學院，株洲412006）

為了解決汽輪機通流部分蒸汽濕度的在線測量問題，提出了一種基于散射相函數的半經驗公式快速反演散射光強分布的計算方法。該算法采用MATLAB自帶的cftool進行相函數的雙高斯擬合，擬合誤差低，且擬合函數可以快速得到Mie散射理論的近似解析解，即從散射光強分布到水滴質量中間半徑的快速反演。結果表明，在約束水滴粒徑范圍內，得到了顆粒大小與散射比之間的半經驗模型，對比實驗測得散射比，吻合良好，且由半經驗模型反演得到水滴質量中間半徑為1.1μm。在一定條件下，可以有效解決蒸汽濕度的在線測量問題。

散射；水滴質量中間半徑；雙高斯擬合；汽輪機

引 言

汽輪機低壓缸常期在濕蒸氣狀態下運行，在濕蒸氣流過葉片時，會造成腐蝕，影響機組經濟、安全運行，降低汽輪機級效率。而對水滴粒徑的在線測量，對于實現汽輪機蒸汽濕度測量，以適時調整汽輪機組蒸汽進口參量，提高機組運行的安全性和經濟性具有重要意義。

自20世紀70年代以來，流動蒸汽濕度的測量技術才取得了較大進展。隨著激光技術、光電技術及計算機技術的迅速發展和廣泛應用，基于激光散射法測量顆粒粒徑分布［1］的技術得到了廣泛應用。由于激光散射法［2-4］具有適用性廣、粒徑測量范圍寬、測量準確、精度高、重復性好、測量速度快、所需知道的被測顆粒及分散介質的物理參量少、儀器的自動化及智能化程度高、可實現在線測量等優點，同樣被應用于汽輪機水滴粒徑的測量中［5-6］。

傳統的水滴粒徑的測量方法是基于Mie散射理論，通過對測量得到的前向小角度散射光強分布進行反演［7］實現的。然而經典Mie散射理論計算量大，且要經過大量迭代，非常耗時，不能滿足實時測量的要求。因此，本文中提出了一種基于散射相函數的半經驗公式快速反演散射光強分布的算法，并采用MATLAB內置命令cftool對水滴群散射相函數進行雙高斯擬合，得到散射相函數近似的半經驗公式，從而建立起水滴粒徑分布與散射光強之間的快捷橋梁，為測量汽輪機低壓缸的蒸汽濕度，提供了快速可行的方案。采用參考文獻［8］中的實驗圖像，分析得到與散射光強分布關聯的實驗散射比，驗證了數值模擬結果。

1 M ie理論與MATLAB數值模擬

在經典Mie散射理論的基礎上，運用參考文獻［8］中的改進算法，充分利用MATLAB的內置命令與函數集，可以實現散射系數、消光系數、散射相函數在任意較寬顆粒粒徑范圍內的快速計算。非偏振光情形下，散射光強表示式為［8］：

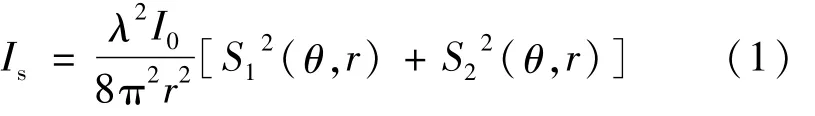
式中，Is為總散射光強，I0為入射光強，λ為激光波長，r為顆粒半徑，S1（θ）和S2（θ）為振幅函數。

將水滴質量中間半徑代入（1）式可數值模擬散射光強值的分布情況。但其逆向解，即實驗測得散射光無法應用文獻方法求得水滴質量中間半徑。在汽輪機通流部分蒸汽濕度在線測量要求下，需尋求Mie散射理論解可替代近似公式。

2 相函數的雙高斯擬合

Mie氏理論在已知散射光強條件下，反演顆粒粒徑分布時，其矩陣為變態矩陣，沒有解析解。因此，為了獲得散射光強的逆向解，這里將水滴的散射相函數作雙高斯擬合，得到擬合公式——半經驗公式。其中，散射相函數是散射光強隨散射角度變化的函數。

［9］中的改進Mie計算方法下，得出散射相函數計算式。當入射光為非偏振光時，其表達式為：

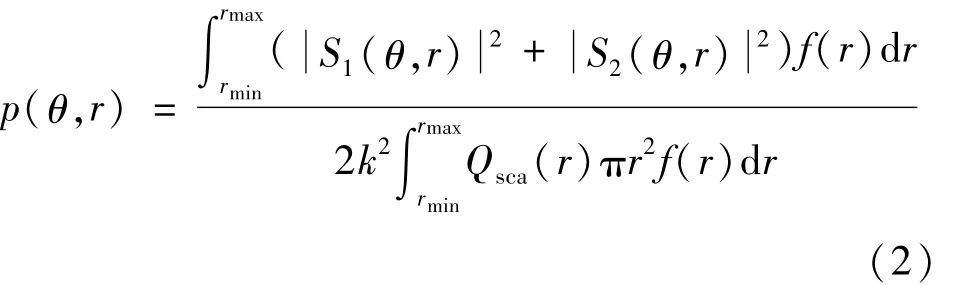
式中，p（θ，r）為散射相函數，θ為散射角，r為顆粒尺寸半徑，m為兩相介質相對折射率（因兩相介質相對穩定，這里不做討論為激光波數，Qsca（r，m）為散射系數，rmax和rmin為水滴半徑的最大值及最小值，f（r）為水滴尺寸分布概率密度函數。f（r）服從羅辛-拉姆勒（Rosin-Rammler，R-R）分布，該分布函數特別適合于描述噴霧形成的液滴群，在一定范圍內是可靠的，其表達式為：

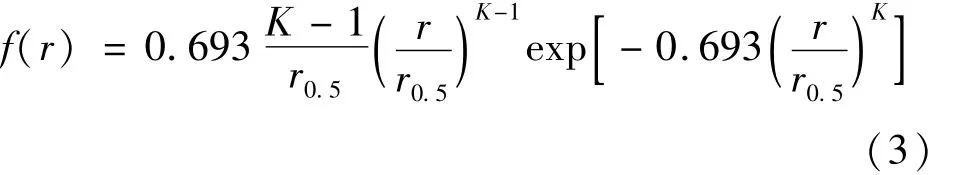
式中，r0.5為水滴質量中間半徑，K為水滴分布的寬度參量。

采用MATALB編程，分別計算了不同波長、水滴質量中間半徑下散射相函數圖像隨角度變化關系曲線，如圖1和圖2所示。從圖中可知：（1）波長越短，散射現像越明顯，且主要集中在前向小角度；（2）水滴質量中間半徑越大，散射現象越明顯，在前向小角度集中分布，且在較大角度處振蕩明顯。

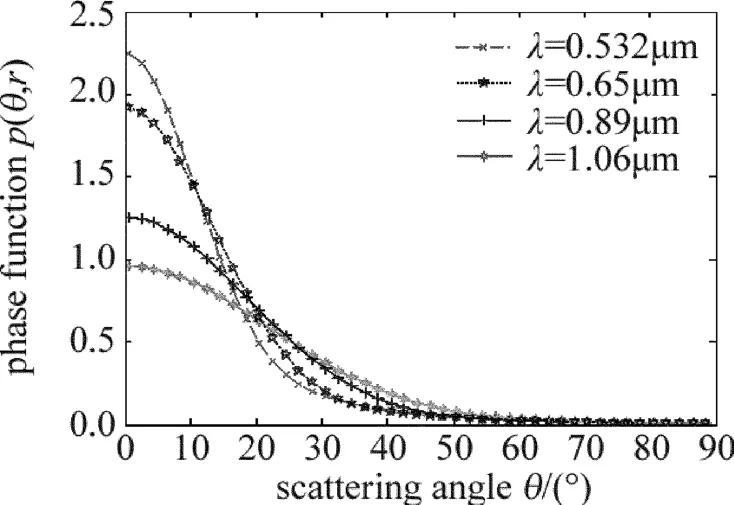
Fig.1 Phase function under differentwave length of scattering

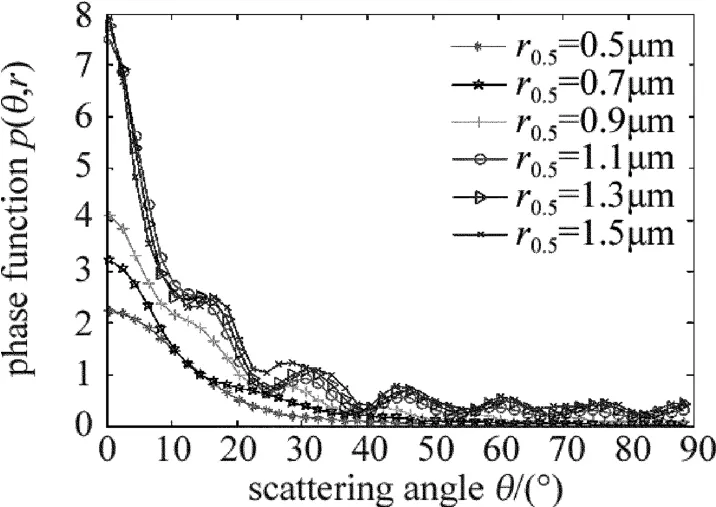
Fig.2 Phase function under differentwater qualitymiddle radius

可見，影響散射光強分布的因素很多，且水滴質量中間半徑是影響蒸汽濕度測量的關鍵因素。在汽輪機低壓缸中，一次水滴粒徑范圍在0.1μm～2μm之間，取水滴質量中間半徑范圍為0.5μm～1.5μm，假定其它參量為定值，如λ＝0.532μm，K＝5，結合（2）式數值模擬r0.5＝0.5μm時散射相函數圖像，如圖3所示，同時采用MATLAB內置命令cftool及函數集在同一圖像上進行高斯擬合及雙高斯（double Gaussian）擬合。擬合結果顯示，采用雙高斯函數擬合結果更為理想。

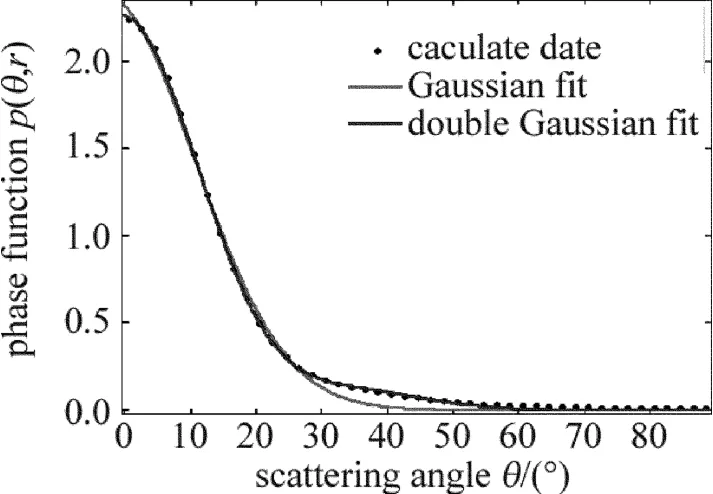
Fig.3 Gaussian fitting and double Gaussian results for phase function

經MATALB內置命令cftool及編程所得雙高斯擬表達式，即相函數近似半經驗公式：

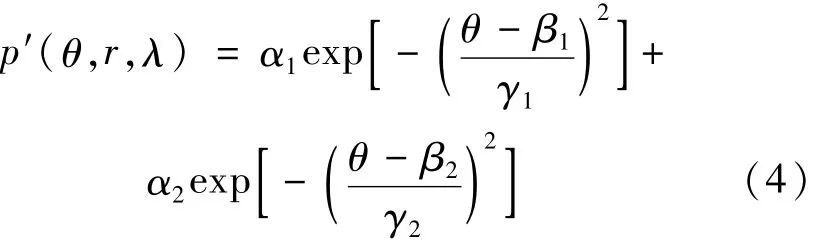
式中，α1，β1，γ1，α2，β2和γ2均為擬合待定參量，p′（θ，r，λ）擬合散射相函數。顯然參量與激光波長、水滴質量中間半徑r0.5等因素有關。當λ取0.532μm，0.65μm，0.89μm，1.06μm時，得到的擬合特定參量與波長相關關系如圖4所示，由于實驗條件及波長的可控因素，僅對λ＝0.532μm進行分析。r0.5在0.5μm～1.5μm范圍內時，擬合參量與半徑相關關系如圖5所示。

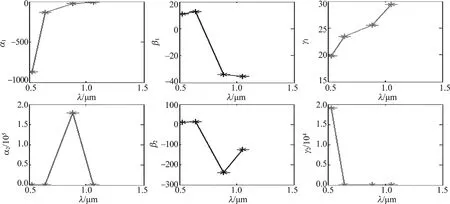
Fig.4 Double Gaussian fitting parameters changing with the laserwavelength

Fig.5 Double Gaussian fitting parameters changing with water qualitymiddle radius

假設散射角為θ時，散射光強為I（θ），擬合散射相函數為p′（θ，r，λ）；散射角為θ0時，散射光強為I（θ0），擬合散射相函數為p′（θ0，r，λ）。可得如下散射比Ks關系式：

在實驗測得散射光強灰度圖像條件下，經轉化得不同散射角θ＝3.4°～5.6°，θ0＝3.2°下，散射光強比值，根據半經驗公式（4）式，應用圖4中雙高斯擬合參量隨水滴質量中間半徑變化關系，便可計算得到水滴質量中間半徑r0.5。以此半徑代入經典Mie散射理論，數值模擬得散射光強值

3 散射比結果分析

在MATLAB開發環境下，為了檢測cftool自帶雙高斯函數反演方法的可靠性，用參考文獻［10］中對模擬汽輪機低壓缸平臺實驗所攝CCD灰度圖像進行分析，并提取灰度曲線，如圖6所示。實驗結果表明，在散射角θ＝3.2°時，灰度值最強，隨后灰度值迅速下降。

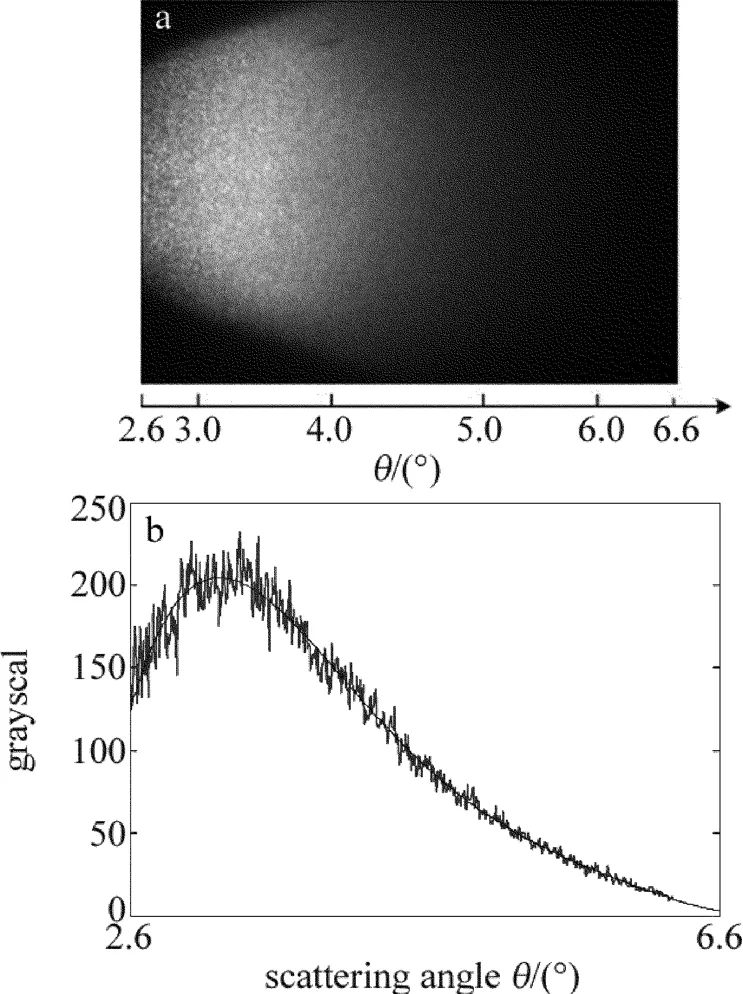
Fig.6 Forward small angle scattering intensity distribution and the axial grayscale

實驗中測得散射比以后，利用相函數半經驗公式推導出的散射比關系（5）式及相函數擬合參量點進行反演［10］，計算在背壓為0.50MPa下，可得濕蒸氣的水滴質量中間半徑為1.1μm。將水滴質量中間半徑代入（1）式，經Mie理論數值模擬得理論散射比，結果如表1所示。

Table1 Under different scattering angle，the scattering ratio results between the experiment and Gaussian fitting

從表1可以看出，由于受大角度孔徑光闌的限制及環境和測量誤差等因素的影響，在散射比為時，實驗值較理論值要小。但總的來說，經半經驗公式反演簡化后，數值模擬散射比結果與實驗測得結果吻合良好。

實驗測得多組散射比，代入（5）式，求出擬合參數值，由擬合參量與水滴質量中間半徑關系，可求得水滴質量中間半徑為r0.5＝1.1μm，采用半經驗公式數值模擬結果與參考文獻［11］中用經典Mie散射理論計算結果相近，說明該方法有效。將反演r0.5＝1.1μm代入以下兩式，便可對汽輪機通流部分蒸汽濕度Y進行計算［8］：

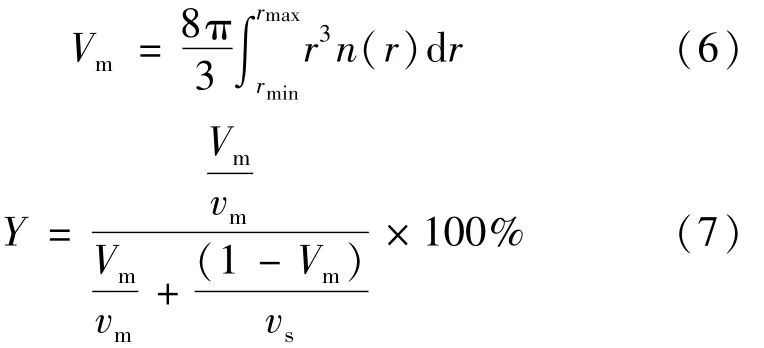
式中，Vm為單位體積內的水滴總容量，n（r）為尺寸分布函數；vm是飽和水的比容，vs是飽和汽的比容，均可通過查表獲取。

4 結 論

針對經典Mie散射理論測量顆粒粒度大小時沒有嚴格解析解情形，這里用MATLAB自帶cftool對相函數進行雙高斯擬合，得出相函數半經驗公式，使Mie理論解變得簡單、快速可解。實驗中測得散射比，經半經驗公式反演得到水滴質量中間半徑為1.1μm，再用于散射相函數數值模擬，計算得散射比。

可以說所求得半徑即為模擬汽輪機低壓缸內水滴顆粒質量中間半徑。

與其它算法相比，其優點表現在：（1）計算簡單，數值模擬結果與實驗結果吻合較好；（2）可以實現汽輪機通流部分蒸汽濕度在線測量問題；（3）具有一定的理論意義和工程實際應用價值。

參考文獻

［1］ KADONO T，ARAKAWA M，KOUCHIC A.Size distributions of chondrules and dispersed droplets caused by liquid breakup：An application to shock wave conditions in the solar nebula［J］.Icarus，2008，197（2）：621-626.

［2］ SIGEL R.Light scattering near and from interfaces using evanescentwave and ellipsometric light scattering［J］.Colloid＆Interface Science，2009，14（6）：426-437.

［3］ GOGOIA，BURAGOHAIN A K，CHOUDHURY A，et al.Laboratorymeasurements of light scattering by tropical fresh water diatoms［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2009，110（14／16）：1566-1578.

［4］ SHCHERBAKOV A A，TISHCHENKO A V.Light scattering in plane dielectric layers：modeling in the 2-D reciprocal space［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2012，113（18）：2424-2430.

［5］ WUW，QIN Sh Q，HUANG Zh Q.A fast inversionmethod forwater droplet size determination in scattering lightmeasurement［J］.Journal of Optics，2011，31（7）：1-5（in Chinese）.

［6］ HUANG Zh Q，YANG JM，SUN Ch Sh.Application of the laser scattering theory for monitoring steam wetness and droplet size in steam turbines［J］.Journal of Power Engineering，2006，26（2）：241-244（in Chinese）.

［7］ CAIW W，ZHAO Y，MA L.Direct recursion of the ratio of Bessel functionswith applications to Mie scattering calculations［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2008，109（16）：2673-2678.

［8］ HUANG Zh Q，QIN Sh Q.Investigation of exhaustwetnessmeasurementmethod in steam turbine based on mie scattering of laser［D］.Changsha：Graduate Schoolof National University of Defense Technology，2010：1-118（in Chinese）.

［9］ ZHANG H Y，ZHAOW J，REN D M，et al.Improved algorithm of Mie scattering parameter based on MATLAB［J］.Journal of Light Scattering，2008，20（2）：102-110（in Chinese）.

［10］ GODDEERIS C，CUPPO F，REYNAERS H，et al.Light scatteringmeasurementsonmicroemulsions：estimation ofdroplet sizes［J］.International Journal of Pharmaceutics，2006，312（1／2）：187-195.

［11］ HUANG Zh Q，CAO X L，YANG JM，et al.Application of CCD in measuring steam moisture and droplet size［J］.Opto-Electronic Engineering，2010，37（4）：39-43（in Chinese）.

Application of fast inversion algorithm in measurement of steam hum idity of steam turbine

LIU Fangyan1，HUANG Zhuqing1，2，CAO Xiaoling1，CAICheng1，YANG Ying1
（1.School of Energy and Power Engineering，Changsha University of Science＆Technology，Changsha 410114，China；2.Hunan Nonferrous Metals Vocational and Technical College，Zhuzhou 412006，China）

In order to solve the problem confronted with the online steam humiditymeasurementof turbine flow pass，a semi-empirical formula of phase function computingmethod was proposed to improve the inversion algorithm on scattering light distribution.Phase function of double Gaussian fitting by using MATLAB with cftool was adopted in this algorithm.The fitting result shows that the relative error is in small，and the approximate analytic solution of the Mie scattering theory could be got by the fitting function，which means that a rapid inversion from the scattering light intensity distribution to water quality radius.According to the results，with the restriction of the range of the droplet size，the approximation of the theory between the droplet size and scattering ratio was got.Contrast experiment showed themeasured scattering ratio was similar with the simulated scattering ratio.Based on the semi-empirical model，the water quality of middle radius was 1.1μm.Thefast inversion algorithm can well resolve the onlinemeasurement of steam humidity.

scattering；water qualitymiddle radius；double Gaussian fitting；turbine

O436.2

A

10.7510／jgjs.issn.1001-3806.2014.03.023

1001-3806（2014）03-0389-05

湖南省自然科學基金資助項目（12JJ2031）；湖南省科技廳重點資助項目（2011GK4005）

劉芳艷（1987-），女，碩士研究生，主要研究方向為光學測量中實驗數據處理及分析。

*通訊聯系人。E-mail：huangzhuqing＠aliyun.com

2013-05-27；

2013-06-21