基于電子式互感器微分輸出的改進R-L模型距離保護算法

陳學偉 高厚磊 向珉江 趙寶光 劉 凱 吳遠波 田 純

（1．山東大學電氣工程學院 濟南 250061 2.萊蕪供電公司 萊蕪 271100）

1 引言

電子式互感器具有不受飽和及鐵磁諧振影響、頻帶寬、動態范圍大、體積小、重量輕、數字量輸出等諸多優點，已開始大量應用于智能化變電站。但基于羅氏線圈的電子式電流互感器（ECT）和基于電容分壓原理的電子式電壓互感器（EVT）的輸出信號皆為被測信號的微分，為還原原始信號，需要在信號處理環節中加入積分環節，由此帶來一定的時間延時和相位偏移，并會降低頻響帶寬和增加高壓側功耗。為克服額外的積分環節帶來的不利影響，本文對傳統R-L 模型算法進行改進，探索直接利用電子式互感器的微分輸出實現故障測距和距離保護的方法。

2 電子式互感器的微分輸出及處理方法

2.1 基于羅氏線圈ECT 的輸出信號

羅氏線圈的等效電路[1,2]如圖1所示，其中，R0為線圈的內阻，L為自感系數，RL為負載電阻，C為匝間電容，e(t)為感應電動勢，Uo為輸出電壓。

根據電磁感應定律，可列式為

式中，M為線圈的互感系數；i為被測電流。

圖1 羅氏線圈等效電路圖Fig.1 Equivalent circuit diagram of Rogowski coils

由圖1所示的羅氏線圈等效電路可列式為

取拉普拉斯變換并化簡得輸入輸出關系為

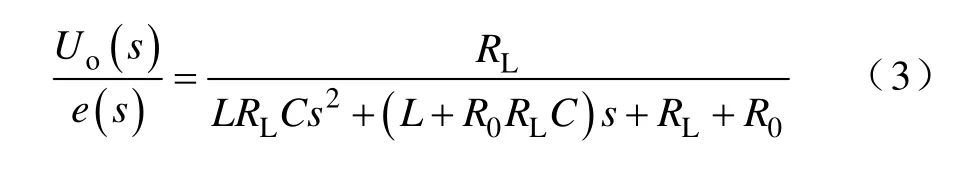
當RL＞＞ωL+R0且1/ωC＞＞ωL+R0時，羅氏線圈處于開路工作狀態，Uo(s)/e(s)=1，拉普拉斯反變換得

此時輸出電壓正比于被測電流對時間的微分，此狀態即為基于羅氏線圈ECT 的外積分工作狀態。在實際應用中，外積分工作方式能實現對脈沖電流、工頻電流和諧波電流的測量，是基于羅氏線圈ECT的主要工作方式。

2.2 基于電容分壓原理EVT 的輸出信號

圖2為基于電容分壓原理EVT 的等效電路圖[3,4]，分壓器的采樣是在C2兩端并聯一個精密取樣電阻R，分壓器的輸出u2與被測電壓u1的關系為

圖2 電容分壓式EVT 等效電路Fig.2 Equivalent circuit diagram of capacitor divider EVT

兩邊取拉普拉斯變換得

若1/R＞＞ω（C1+C2），則有U2/R=sC1U1，拉普拉斯反變換得

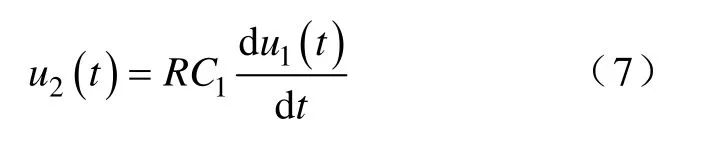
由式（7）可知電容分壓EVT 的輸出電壓與被測電壓對時間的微分成正比。

2.3 電子式互感器輸出信號的處理方法

圖3為電子式互感器高壓側數據處理流程圖。電子式互感器輸出的模擬信號經前置濾波裝置濾波后，通過模擬積分電路還原出原始信號，再通過A-D模塊轉換為數字信號，最后經電-光變換轉換為光信號后通過光纖傳輸到低壓側供保護裝置使用。

圖3 高壓側數據處理流程圖Fig.3 Data processing flow diagram of high-voltage side

圖3中的積分環節需要一定的數據窗長度及數據處理時間，因而會降低保護的動作速度；此外，積分電路還會限制信號傳輸帶寬，增加高壓側功耗。針對上述問題，如能設計出直接利用微分信號的保護算法，則保護裝置可直接接收電子式互感器輸出的微分信號，從而省去模擬積分電路環節。

3 R-L 模型算法原理及其改進

3.1 傳統R-L 模型算法原理

R-L 模型算法主要用于計算線路阻抗。對于一般的輸電線路，短路情況下，線路分布電容產生的影響主要表現為高頻分量，如果采用低通濾波器將高頻分量濾除，就相當于可忽略分布電容的影響，將輸電線路等效為R-L 模型[5,6]，如圖4所示。

圖4 R-L 模型示意圖Fig.4 Schematic diagram of R-L model

K 點發生接地短路時，以下關系成立。

式中，R1、L1分別為保護安裝處到故障點間的正序電阻和電感；u(t)、i(t)分別為保護安裝處測得的電壓和電流。

分別取兩個不同時刻的電壓、電流和電流導數，可列式

式中，u1、u2、i1、i2分別為電壓、電流在t1、t2時刻的采樣值；D1、D2分別為電流i1、i2在t1、t2時刻的導數值（導數的求取可用差分算法實現）。

由式（9）可求得

根據公式：X1=2πfL1，可求出故障線路的正序電抗，從而實現故障測距及距離保護的相關功能。

3.2 改進R-L 模型算法原理

為直接應用電子式互感器傳感頭輸出的微分信號，對傳統R-L 模型算法進行改進。對式（8）兩端微分，可得

式中，du/dt和di/dt是由電子式互感器傳感頭直接獲得的數據，而d2i/dt2是對di/dt求導而得的數據。傳統R-L 模型算法需增加兩組積分電路同時對ECT和EVT 輸出的微分信號進行還原，而改進算法只需對ECT 的輸出信號進行一次微分，且微分過程的數據窗長度根據實際需要可靈活調整，不會限制信號的傳輸帶寬。

取兩個不同采樣時刻的數據，代入式（11）解得

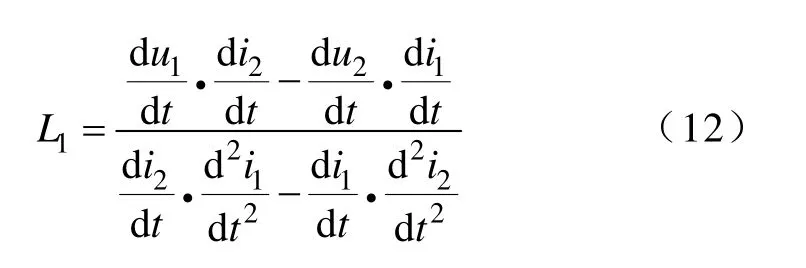
實際應用中，對于相間短路，應采用Δu和Δi。例如AB 兩相短路時，取uab和ia-ib。對于單相接地短路，取相電壓及相電流加零序補償電流。以A 相為例，式（8）改寫成

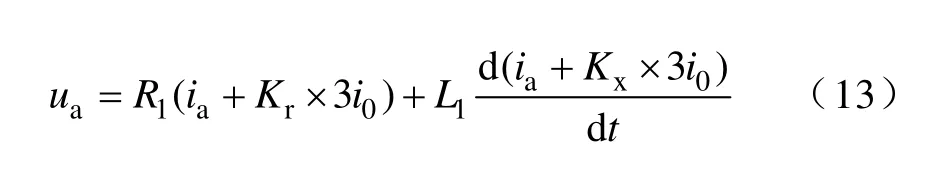
式中，Kr、Kx分別為電阻及電感分量的零序補償系數，Kr=(r0-r1)/(3r1)，Kx=(l0-l1)/(3l1)，其中r0、r1、l0和l1分別為輸電線路每km 的零序及正序電阻和電感。

同樣，將式（11）改寫成

取兩個不同采樣時刻數據，代入式（14）可得出與式（12）類似的結果，再根據公式X1=2πfL1，可求得故障線路的正序電抗。

4 計及過渡電阻的影響分析

上節的討論是在假定輸電線路發生金屬性短路基礎上的，但實際發生的短路一般存在過渡電阻Rg[7,8]，如圖5所示。

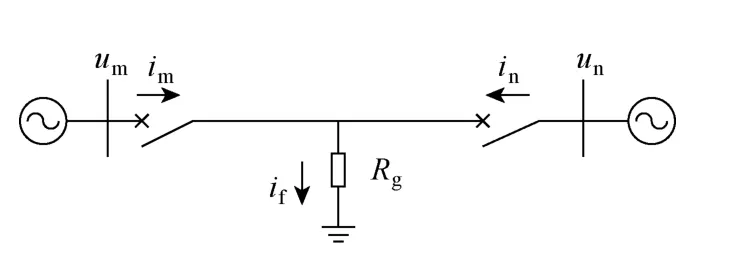
圖5 經過渡電阻接地短路Fig.5 Short circuit through fault resistance

按圖5所標變量可列式為

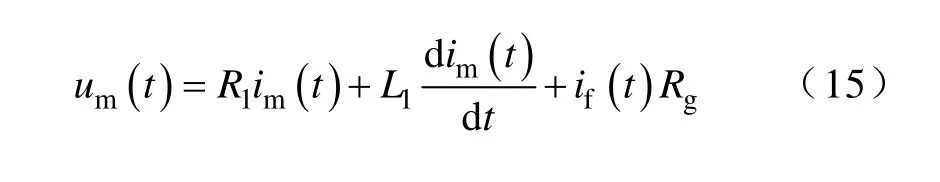
又if=im+in，若兩側電壓相角差不大（＜5°），且系統阻抗角與線路阻抗角接近時，if與im近似同相位。設if=Kim，則K近似為常數。

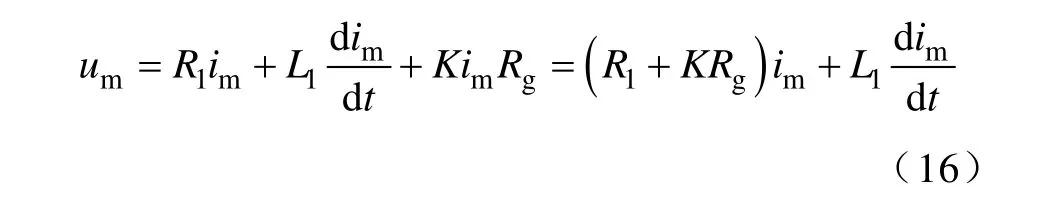
對式（16）兩端微分得

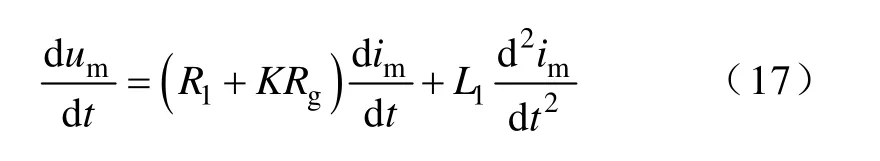
式（17）即為計及過渡電阻的改進R-L 模型算法的計算公式。其中dum/dt和dim/dt可由電子式互感器的輸出直接獲取，而d2im/dt2為對電子式電流互感器輸出數據微分所得。分別取兩個不同時刻數據即可解出（R1+KRg）和L1的值。在if與im接近同相位時，用式（17）計算所得的電抗值是準確的，即可用電抗法較為準確地進行故障測距。

5 改進R-L 模型算法的實驗驗證

5.1 基于PSCAD/EMTDC 的仿真實驗驗證

為驗證改進R-L 模型算法的可行性和有效性，本文采用PSCAD 建模仿真[9,10]，應用Matlab 進行數據處理，并以基于阻抗原理的傅里葉算法作為參照進行對比分析。仿真模型及參數如圖6所示。

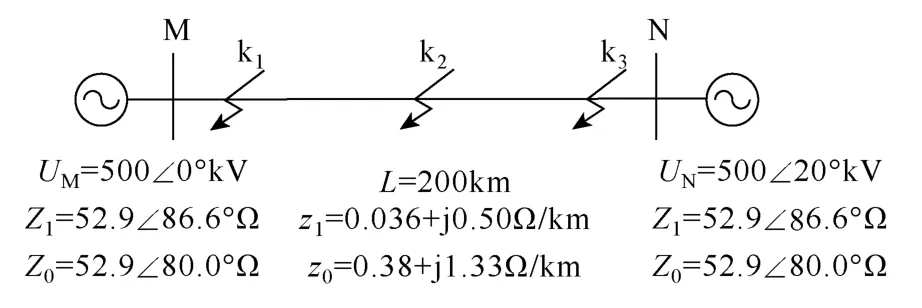
圖6 仿真模型及參數Fig.6 Simulation model and parameters

依照圖6所示仿真模型及參數進行仿真，通過對電壓電流進行微分處理來模擬電子式互感器的微分輸出，將相關數據結果導入到Matlab 中進行處理。其中傅里葉算法的數據窗長度為一周期（20ms），而改進R-L 模型算法兩采樣時刻t1、t2時差為2ms，均值濾波數據窗為1/4 周期（5ms），共7ms。設故障測距相對誤差計算公式為

表1、表2分別為線路出口（距離M 端10km）、中端（距離M 端100km）和末端（距離M 端180km）分別發生AN 金屬性短路和經過渡電阻（Rg=100Ω）短路，傅里葉算法和改進R-L 模型算法的測距結果及誤差。其中，表1、表2分別為兩端電源相角差為20°和5°時的測量數據。

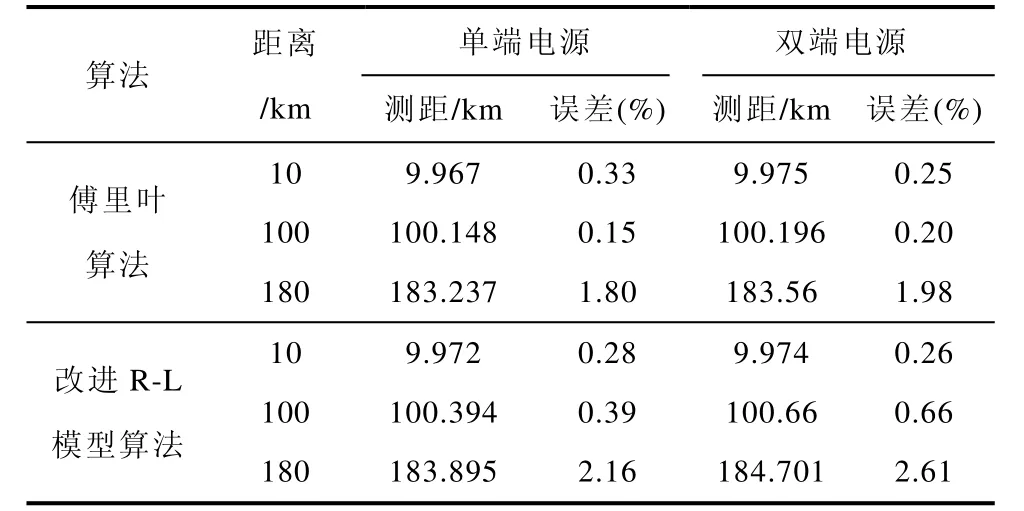
表1 故障測距仿真結果（Rg=0Ω）Tab.1 Fault location simulation results（Rg=0Ω）

表2 故障測距仿真結果（Rg=100Ω）Tab.2 Fault location simulation results（Rg=100Ω）

由表1 可知，在發生金屬性短路時，無論是單端電源還是雙端電源，兩種測距算法的相對誤差均很小（＜3%），測量結果精確可靠。

分析表2，在發生經過渡電阻短路時，對于單端電源系統，改進R-L 模型算法誤差非常小，幾乎與無過渡電阻時相同；對于雙端電源系統，在兩側電源相位差很小且系統阻抗角與線路阻抗角接近的條件下，改進R-L 模型算法測距結果對于單端測距算法而言也足夠準確（＜3%或＜3km）。而對于傅里葉算法，無論是單端電源系統還是雙端電源系統，均已無法正確測量。

此外，與傅里葉算法相比，改進R-L 模型算法的數據窗長度僅為傅里葉算法的1/3，從原理上提高了保護的動作速度。

5.2 算法的動模實驗驗證

為驗證改進R-L 模型算法在實際系統中的測距精度與可靠性，在動態模擬實驗室中搭建與實際系統按比例匹配的物理模型，如圖7所示。

圖7 動模實驗模型及參數Fig.7 Dynamic simulation model and parameters

圖7中，右側為發電機系統，通過單回線并于左側系統，模擬線路全長200km。其中，K1為線路中點（100km）的故障點，模擬阻抗比（實際線路阻抗/設計元件阻抗）為6.6，兩側母線處均以1kV電壓模擬實際線路500kV 電壓，線路參數如圖中所示。DL1、DL2為斷路器，故障類型和故障時間可靈活設定，電壓取自系統側母線EVT，電流取自線路ECT。

表3 所示為在100km 處AN 故障時不同過渡電阻條件下兩種測距算法的動模實驗測距結果對比。

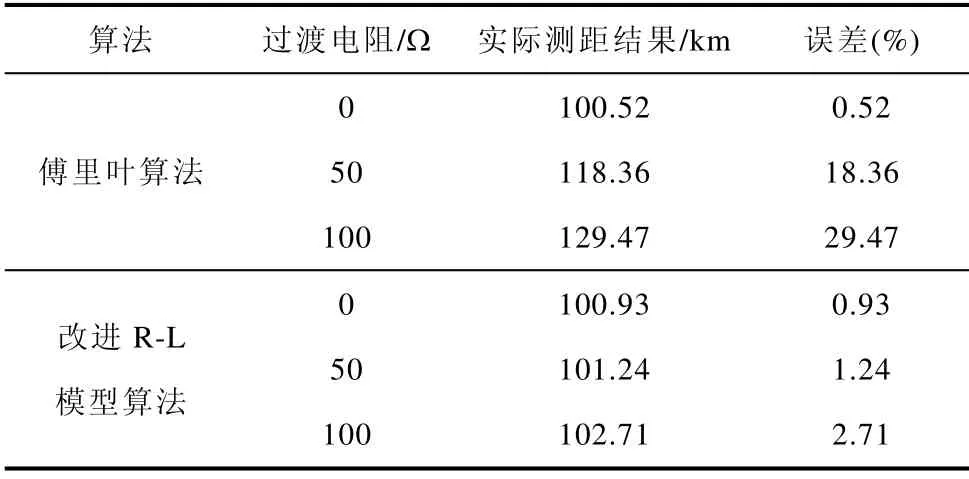
表3 動模實驗測距結果Tab.3 Fault location results of dynamic simulation experiment

由表3 結果可知，動模實驗驗證了改進R-L 模型算法在金屬性短路和經過渡電阻短路時測距的可靠性和精確性，測距相對誤差小于3%；傅里葉算法在金屬性短路條件下測距結果準確，當存在過渡電阻時，測距誤差急劇增大，使測距失效。

6 算法的動態特性

對于距離保護來說，要準確獲得故障線路阻抗，所依據的原始數據應是故障后的電流和電壓數據。對于與數字濾波器配合應用的算法，濾波器和算法所需的總數據窗都應取故障后的數據。

輸電線路發生故障所引起的電壓電流的相關變化是一個連續的過程，利用各種算法實時算得的線路阻抗值也是不斷變化的，即從負荷阻抗逐漸變為短路阻抗的過程。因此，短路后測得準確的線路阻抗值至少需要與算法數據窗相當的時間延時。

研究算法動態特性的目的是確定利用部分故障前數據、部分故障后數據計算得到的線路阻抗值是否單調下降[11,12]。若是單調下降，計算值低于整定值就可以立即跳閘，甚至可利用反時限特性進一步縮短跳閘時間，如圖8a 所示；反之，若算法的動態特性非單調下降，則在故障后一個數據窗（0～N）時間內的計算值可能比實際短路阻抗小，則在有一次計算值低于整定值就跳閘時，將可能導致保護誤動作，如圖8b 所示。

圖8 動態特性圖Fig.8 Dynamic characteristics graph

為進一步對比分析，繪制傅里葉算法和改進R-L 模型算法的電阻、電抗動態特性如圖9所示。圖9中采用雙端電源線路中段（距離M 端100km處）發生AN 金屬性短路故障時的數據，采樣頻率為400 點/周期。

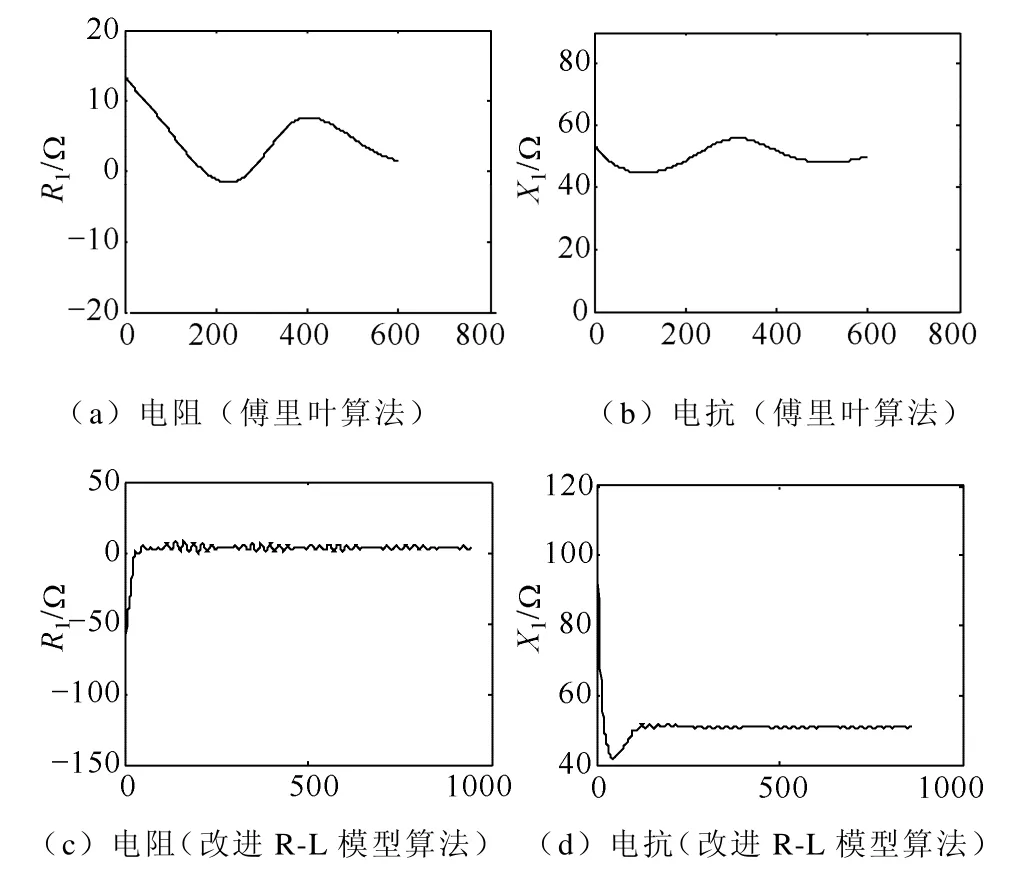
圖9 仿真動態特性圖Fig.9 Dynamic characteristics graph of simulation

由圖9a、圖9b 可以看出，傅里葉算法計算所得的電阻和電抗值近似呈正弦曲線變化，這樣的動態特性極易引起保護的誤動作。

由圖9c、圖9d 可以看出，改進R-L 模型算法的短路電阻和短路電抗曲線在穩定后也是振蕩變化的，但振蕩周期和幅值較傅里葉算法低得多，因此能在更短的時間內準確求出故障線路的短路阻抗。由圖9d 還可看出，電抗的動態特性曲線并非單調下降的，而是在0～100 點（故障后0～5ms）內取得極小值（約42?），小于穩定后的短路電抗（約50?）。這就意味著不能在一次計算值低于定值時就跳閘，至少應在連續幾次計算值都在定值以下才可跳閘，但這樣勢必會增加一定的動作時間。

為作進一步分析比較，繪制兩種算法測得的短路阻抗在方向圓特性阻抗繼電器中的動態特性曲線，如圖10所示。

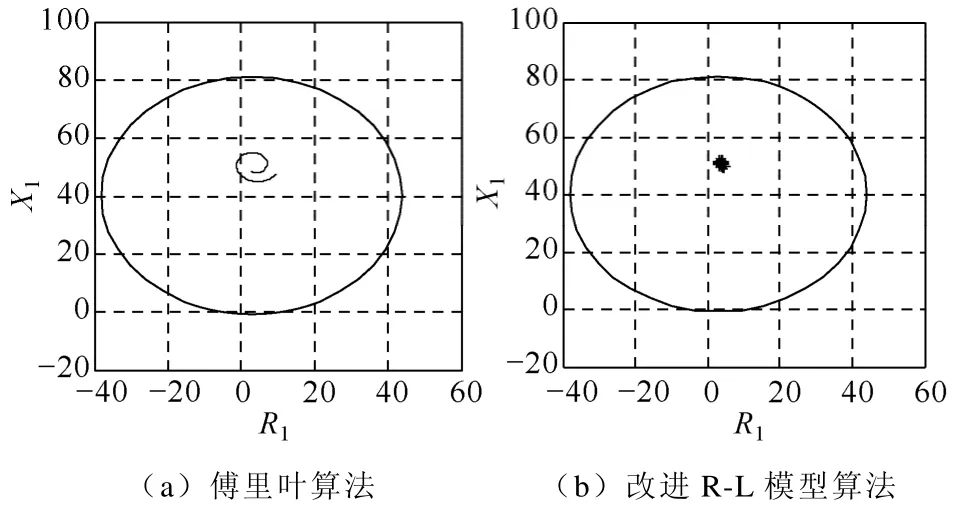
圖10 阻抗動態特性曲線Fig.10 Dynamic characteristics curve of impedance

由圖10可看出，傅里葉算法的阻抗特性曲線近似呈周期變化，因此不易快速準確進行故障測距，而改進 R-L 模型算法的阻抗特性曲線分布非常集中，方便進行快速精準的故障測距。

7 結論

根據電子式互感器具有直接輸出微分信號的特點，本文在傳統 R-L 模型算法基礎上提出了改進R-L 模型故障測距及距離保護算法。理論分析、仿真實驗以及動模實驗結果表明，改進算法繼承了傳統算法的優點，能正確測量輸電線路短路阻抗，具有較好的抗過渡電阻能力，不必濾除非周期分量。與傅里葉算法相比，所用數據窗更短，測距結果更精確；與傳統R-L 模型算法相比，避免了積分環節帶來的不利影響，有利于距離保護的快速動作。此外，基于該方法的保護可直接利用電子式互感器的微分信號，有利于簡化互感器遠端模塊的電路設計。

但是，改進R-L 模型算法也存在一些有待于進一步研究解決的問題。如雙端電源系統，當兩端系統相位差較大且經大過渡電阻接地故障時，測距結果不夠準確。

[1]王寶誠,王德玉,鄔偉揚.羅氏線圈的頻率特性分析與傳感器的設計方法[J].電工技術學報,2009,24(9):21-27.

Wang Baocheng,Wang Deyu,Wu Weiyang.Frequency response analysis of a Rogowski coil transducer and its design method[J].Transactions of China Electrotech- nical Society,2009,24(9):21-27.

[2]李維波,毛承雄,余岳輝,等.羅氏線圈在高速大功率電流檢測系統中的特性研究[J].電工技術學報,2006,21(6):49-53.

Li Weibo,Mao Chengxiong,Yu Yuehui,et al.Study of property of Rogowski coil applied for measuring the switching current of RSD device[J].Transactions of China Electrotechnical Society,2006,21(6):49-53.

[3]王紅星,張國慶,蔡興國,等.電容分壓型電子式電壓互感器研究與設計[J].電力自動化設備,2009,29(10):83-87.

Wang Hongxing,Zhang Guoqing,Cai Xingguo,et al.Electronic capacitive voltage transformer[J].Electric Power Automation Equipment,2009,29(10):83-87.

[4]李延冰.電子式互感器原理、技術及應用[M].北京:科學出版社,2009.

[5]索南加樂,齊軍,陳福鋒,等.基于 R-L 模型參數辨識的輸電線路準確故障測距算法[J].中國電機工程學報,2004,24(12):119-125.

Suonan Jiale,Qi Jun,Chen Fufeng,et al.An accurate fault location algorithm for transmission lines based on R-L model parameter identification[J].Proceedings of the CSEE,2004,24(12):119-125.

[6]索南加樂,劉文濤,陳勇,等.基于 R-L 模型誤差的自適應距離保護[J].電力系統自動化,2006,30(22):66-72.

Suonan Jiale,Liu Wentao,Chen Yong,et al.Adaptive distance protection based on R-L model error[J].Automation of Electric Power Systems,2006,30(22):66-72.

[7]李風光.距離保護躲過渡電阻能力研究[J].電力系統保護與控制,2011,39(8):124-127.

Li Fengguang.The capacity of distance protection hiding from transition resistance[J].Power System Protection and Control,2011,39(8):124-127.

[8]柴濟民,鄭玉平,吳通華.交流1000kV 特高壓輸電線路距離保護特殊問題[J].電力系統自動化,2007,31(12):55-60.

Chai Jimin,Zheng Yuping,Wu Tonghua.Problems in the distance relay for 1000kV UHV AC transmission lines[J].Automation of Electric Power Systems,2007,31(12):55-60.

[9]陳明,張濤.基于R-L 模型算法的距離保護研究與PSCAD 仿真[J].電力學報,2010,25(2):167-170.

Chen Ming,Zhang Tao.Study of distance protection based on R-L model algorithm and its simulation inPSCAD[J].Journal of Electric Power,2010,25(2):167-170.

[10]哈恒旭,張保會,呂志來.高壓輸電線路單端測距新原理探討[J].中國電機工程學報,2003,23(2):42-45.

Ha Hengxu,Zhang Baohui,Lü Zhilai.A novel principle of single-ended line fault location technique for EHV transmission systems[J].Proceedings of the CSEE,2003,23(2):42-45.

[11]黃景光,董蘭蘭,呂艷萍.基于Matlab 的計算機距離保護微分方程算法仿真與研究[J].繼電器,2006,34(5):13-16.

Huang Jingguang,Dong Lanlan,Lü Yanping.Simulating and studying differential equation algorithms of the digital computer distance relaying protection based on Matlab[J].Relay,2006,34(5):13-16.

[12]王賓,董新洲,周雙喜,等.特高壓交流輸電線路接地阻抗繼電器動作特性分析[J].電力系統自動化,2007,31(17):45-49.

Wang Bin,Dong Xinzhou,Zhou Shuangxi,et al.Analysis of ground impedance relay operation characteristics for UHV AC transmission lines[J].Automation of Electric Power Systems,2007,31(17):45-49.