基于新型電壓電流雙閉環控制的軸帶發電機PWM 整流器研究

石健將 李榮貴 張 平 劉莉飛 楊平西

（1.浙江大學電氣工程學院 杭州 310027 2.中國船舶重工第704 研究所 上海 200031）

1 引言

現代船舶推進系統中，為了提高化石燃料利用率，原動機不但給船舶提供動力，還通過帶動軸帶發電機發電給船舶供電，即混合推進系統。軸帶發電機一般由永磁發電機和背靠背的變流器組成，首先電機側變流器對軸帶發電機產生的交流電進行整流，再通過網側變流器逆變產生滿足要求的電能供給船舶用電設備。

電機側變流器采用電壓型PWM 整流器，以滿足交流側單位功率因數、電流正弦化、輸出直流電壓穩定可控、能量雙向流動等要求[1-3]。三相電壓型PWM 整流器按照控制形式可分為間接控制和直接控制[4]；前者主要采用幅相控制[5-8]，而后者根據內環的反饋量又可以分為電壓電流雙閉環控制（VOC）[9]和直接功率控制（DPC）[10-13]。

傳統的VOC 系統在控制器參數合理設計的條件下可以獲得較好的穩態性能，但是受到級聯雙閉環控制以及PWM 整流器的非最小相位（RHP）系統特性[14]的限制，使得傳統雙閉環控制器參數不能設置過大，否則會引起系統的不穩定；為改善傳統電壓電流雙閉環控制的動態性能，很多學者提出了基于負載電流前饋、電流最優控制等方案[15-17]，但是需要外加電流傳感器或者使數字實現復雜化；同時，與電機的直接轉矩控制相仿[18]，有學者提出直接功率控制，也獲得了較好的穩態和動態性能，但是永磁軸帶發電機輸出接口為電力電子變流器，電壓不易測量使得不能直接進行功率測量計算。

為此，本文在傳統的電壓型PWM 整流器的雙閉環控制模型的基礎上提出一種基于電壓電流平方雙閉環的控制策略以提高 PWM 整流器的動態性能，并且通過仿真與實驗驗證了該模型的正確性以及控制方案的可行性。

2 軸帶發電機PWM 整流器的模型

與傳統的三相三橋臂電壓型PWM 整流器拓撲[2]相似，只是軸帶發電機可以缺少了外部的濾波電感，而直接利用永磁軸帶發電機的定子電樞電感作為濾波電感，其整流器拓撲如圖1 所示。

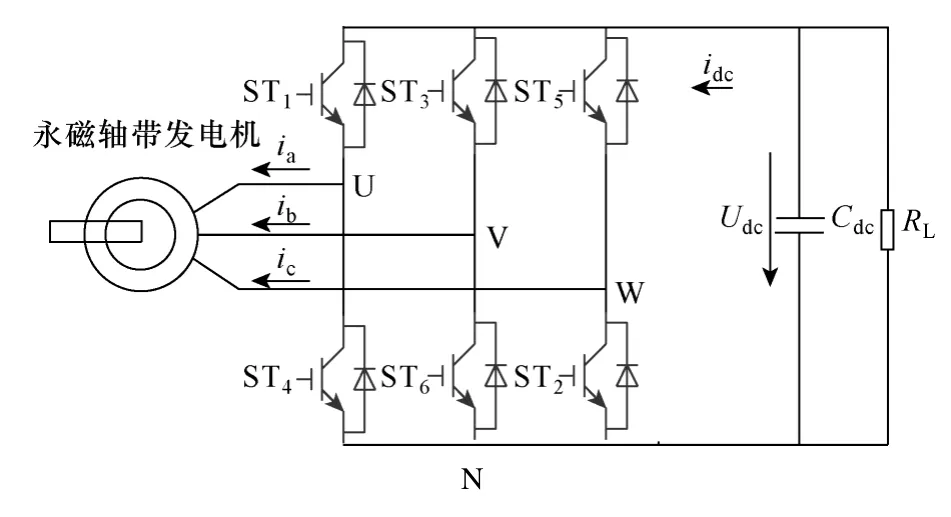
圖1 永磁軸帶發電機PWM 整流器拓撲Fig.1 Topology of PWM rectifier of PM shaft-generator

永磁軸帶發電機的等效模型（電動機慣例）如圖2 所示。其中ea、eb、ec為轉子磁場產生的等效反電動勢（e=-dΦ/dt），Rx（x=a,b,c；Ra=Rb=Rc=R）為等效電樞繞組電阻，lx(x=a,b,c)為等效相電樞電感 L和漏感 Lδ之和，即 la=lb=lc=Lδ+L，Mij（i,j=a,b,c；Mab=Mbc=Mab=-0.5L）為等效電樞互感。

圖2 永磁軸帶發電機等效模型Fig.2 Equivalent model of PM shaft-generator

軸帶發電機PWM 整流器在dq 旋轉坐標軸下的數學模型為

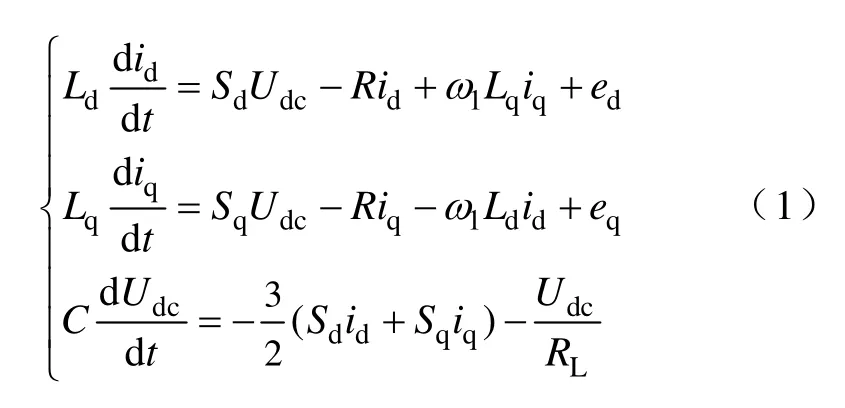
3 新型雙閉環控制策略分析

3.1 傳統雙閉環控制模型分析

從式（1）可知，由于存在狀態變量間的非線性關系，狀態方程又相互耦合，為此文獻[14]通過引入非線性的前饋補償將其去耦化，即令

則式（1）可以化簡為

再對式（2）進行小信號線性化處理得s 域的數學簡化模型[19]為

綜合上述分析可得基于傳統電壓電流雙閉環的解耦控制原理框圖，如圖3 所示。

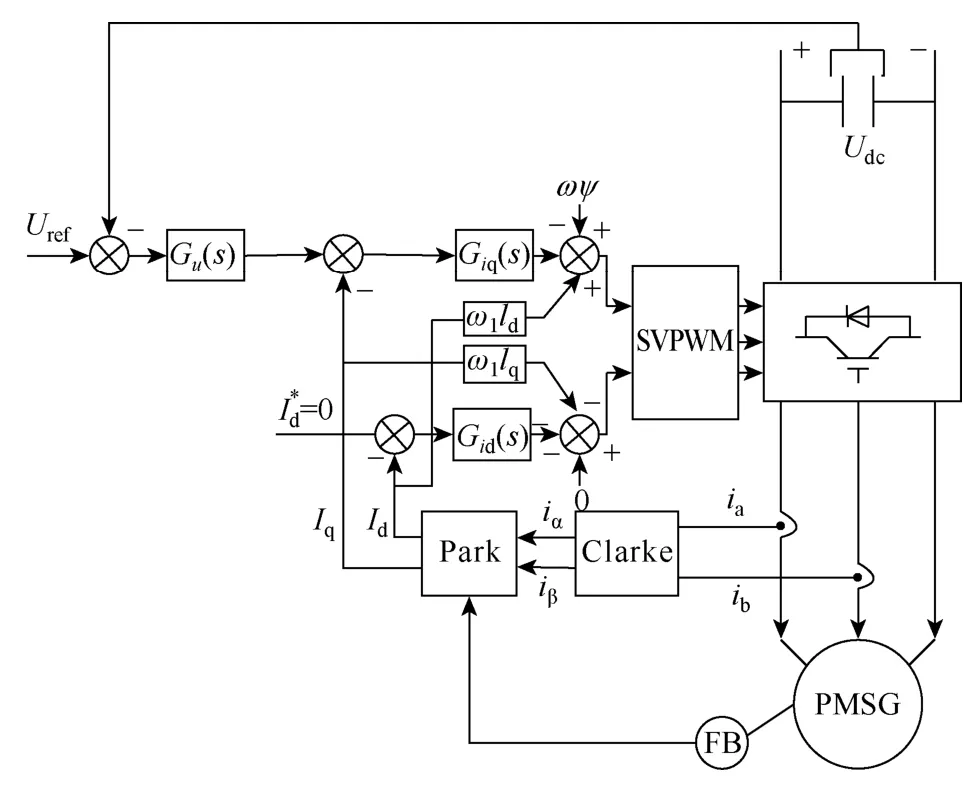
圖3 基于傳統雙閉環控制的原理框圖Fig.3 Schematic diagram based on traditional dual-loop control

3.2 新型雙閉環控制模型分析

根據式（1）和圖3 可知，對于傳統電壓電流雙閉環控制系統中，采用的是采樣所得的電壓電流直接作為反饋控制量，本文在此基礎上對其控制模型進行變換，而采用的是狀態量的平方作為反饋控制量，同時對控制模型進行了簡化。

由式（1）的等式兩邊同時乘以各自的狀態變量，可得

對于電壓環建模可對式（4）進行聯合變換得

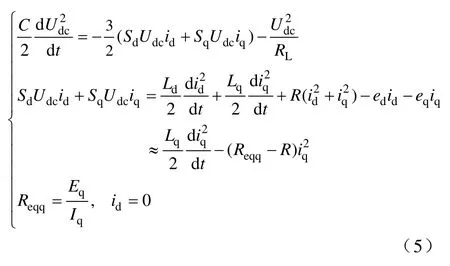
式中，Reqq表示在額定條件下，整流器交流側功率傳輸方向及大小的一個等效常數。

由上式（5）則可推得

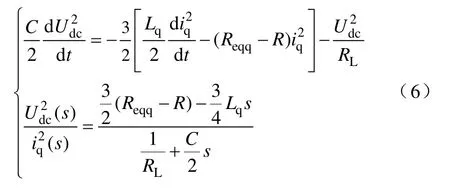
由式（6）可知電壓平方對電流平方的傳遞函數為一非最小相位系統，即RHP 系統，其在額定功率條件下對應的零點關系式為

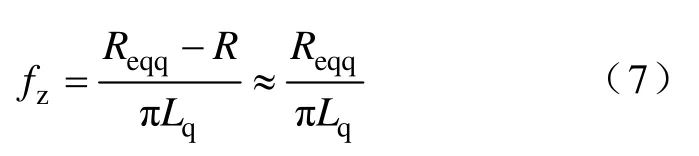
由于非最小相位系統中零點的Bode 圖是以幅值增益20dB 上升，而相位裕度則下降90°，使得系統在重載的條件下不易穩定導致振蕩[14]，為此一般在電壓校正器中加入一個最小相位的極點，使高頻段衰減增益不變，提高系統的穩定性，同時也正是由于該非最小相位零點的存在使得控制系統的整體帶寬也受到了限制。

對于電流環模型也可由式（4）轉換為

分析式（8）可知，等式中雖然存在耦合項 ω1iqdi，但其耦合值在頻率和電感一定時與交直軸電流乘積成一定的比例關系，并且在雙閉環控制系統中為實現發電機輸出功率因數接近1 而控制直軸電流id為0，所以該耦合項 ω1iqdi在穩態過程中約等于0；而該耦合項在動態過程中的值相比控制給定值小得多，也可近似為0。綜上分析，忽略耦合項后電流傳遞函數可進一步簡化為

比較電壓電流平方模型（見式（6）和式（9））與傳統的電壓電流模型（見式（3））可知，前者的時間常數為后者的一半；并且采用如圖4 所示的電壓電流平方控制方案后，由于將控制量的數值平方作為反饋量和給定量，其效果等效于增加控制器直流增益但卻不影響系統穩定性；如此，可以定性地描述為把原控制量的數值平方作為新的控制量，尤其當反饋值與給定值之間的誤差大于1 時，其平方值比較誤差將明顯增大，這樣經過放大的誤差通過PWM 調制，使得輸出控制量快速跟隨其給定值，極大加快了系統的響應速度。綜上所述，基于電壓電流平方的雙閉環控制策略相比傳統的電壓電流雙閉環控制策略的優點，在于相同的控制器參數設計方法下具有更快的系統響應速度，并且不改變系統原有的穩定性。

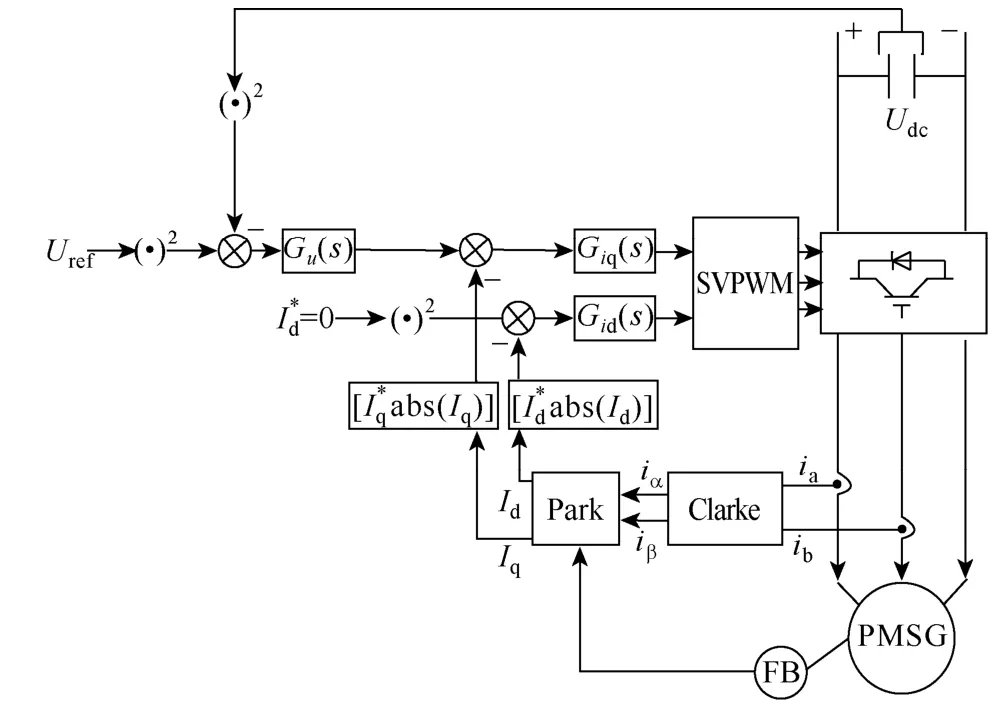
圖4 基于新型雙閉環控制方案原理框圖Fig.4 Schematic diagram based on novel dual-loop control

對于雙閉環控制器的參數設計可以采用典型方法進行整定，其中內環可以整定為典型Ⅰ階環節以滿足快速跟蹤能力，電壓環可以整定為典型Ⅱ階環節以滿足抗干擾要求，同時在級聯雙環控制中要求內環帶寬大于外環帶寬以符合系統穩定性要求。

4 基于Simulink 仿真研究

為驗證該控制方案的可行性與正確性，有必要在Matlab_Simulink 平臺下構建仿真模型，分別對電壓電流平方雙閉環控制方案和傳統電壓電流雙閉環控制方案進行仿真比較研究。

主要仿真參數如下:永磁軸帶發電機額定功率Pn=3.3kW，額定相電壓Un=110V，頻率f=50.0Hz，相數m=3，極對數p=4，定子電阻Rs=0.03Ω，直軸電感 Ld=2mH，交軸電感 Lq=2mH；開關頻率fs=10kHz。

根據典型Ⅰ階、Ⅱ階系統分別整定校正兩種控制系統的控制器參數。傳統控制方案:電流環kp=5.237，ki=78.556；電壓環kpu=0.2，kiu=1.0。電壓電流平方控制方案:電流環kp=5.237/2，ki=78.556；電壓環kpu=0.2/4，kiu=1.0。

圖5 和圖6 分別為兩種控制方案的仿真波形。

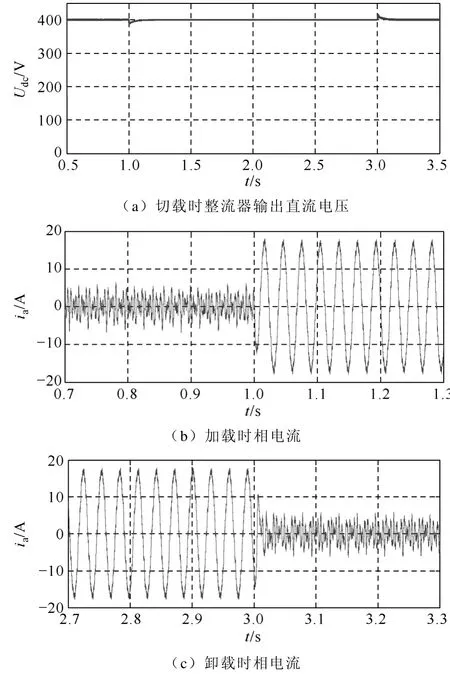
圖5 基于電壓電流平方雙閉環控制的仿真波形Fig.5 Simulation waveforms based on square of voltage-current dual-loop control

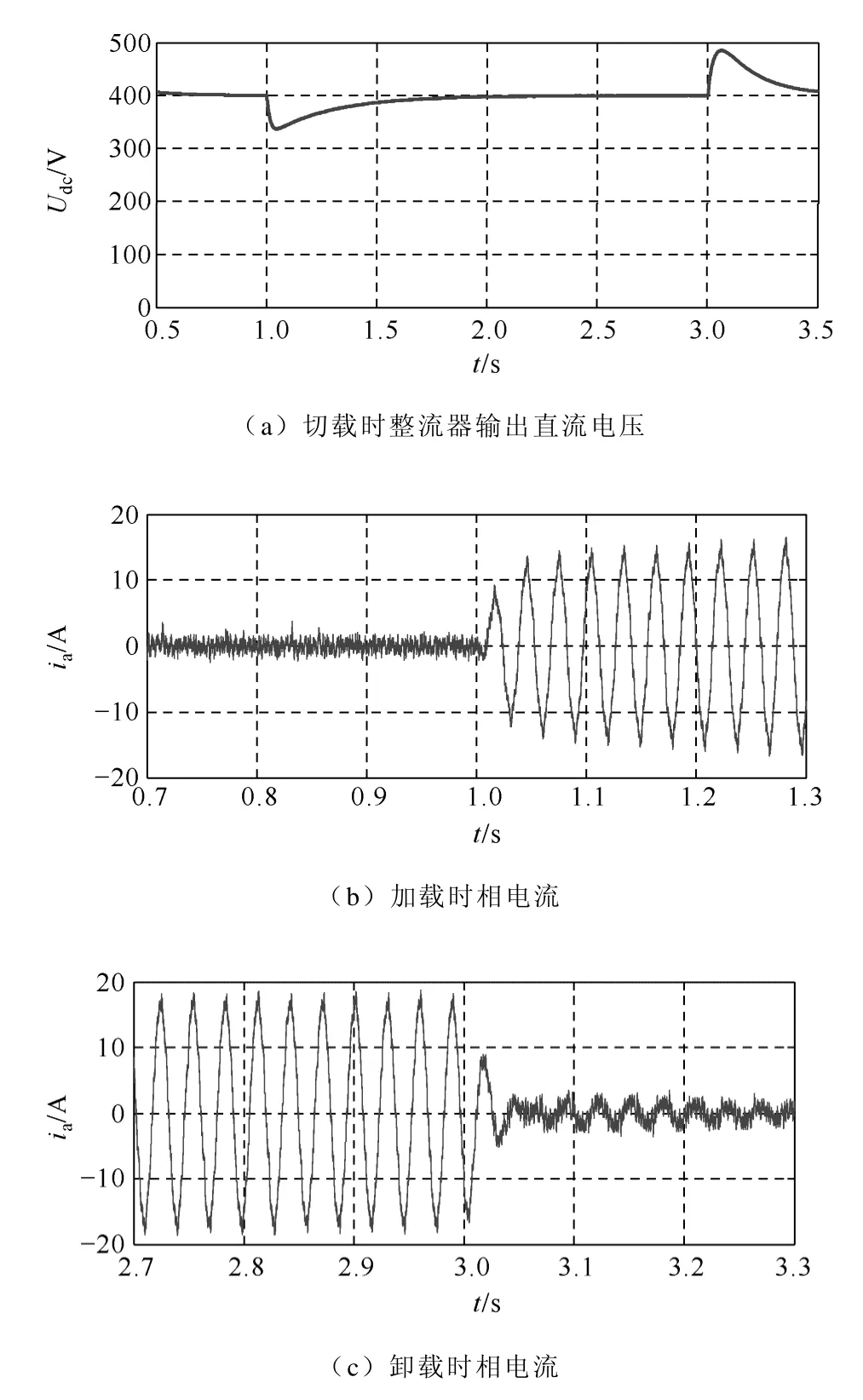
圖6 基于傳統電壓電流雙閉環控制的仿真波形Fig.6 Simulation waveforms based on traditional voltage-current dual-loop control

仿真結果表明:在控制器參數整定設計方法一致的條件下，兩種控制方案在穩態情況下均可以實現PWM 整流器輸出直流電壓的零靜差控制，但在動態過程中前者直流側電壓變化幅值比較后者要小得多；以上比較可知基于電壓電流平方雙閉環控制的動態響應速度優于基于傳統的電壓電流雙閉環控制。

5 實驗驗證

為進一步研究該控制方法的可行性，根據仿真模型參數，本文設計搭建了額定功率為3.3kW 的原理樣機，輸出直流母線電壓為400V，直流側電容取為1 960μF，采用TMS320F28335DSP 作為數字控制芯片，開關頻率為10kHz。

圖7 和圖8 分別為兩種控制方案的實驗波形。

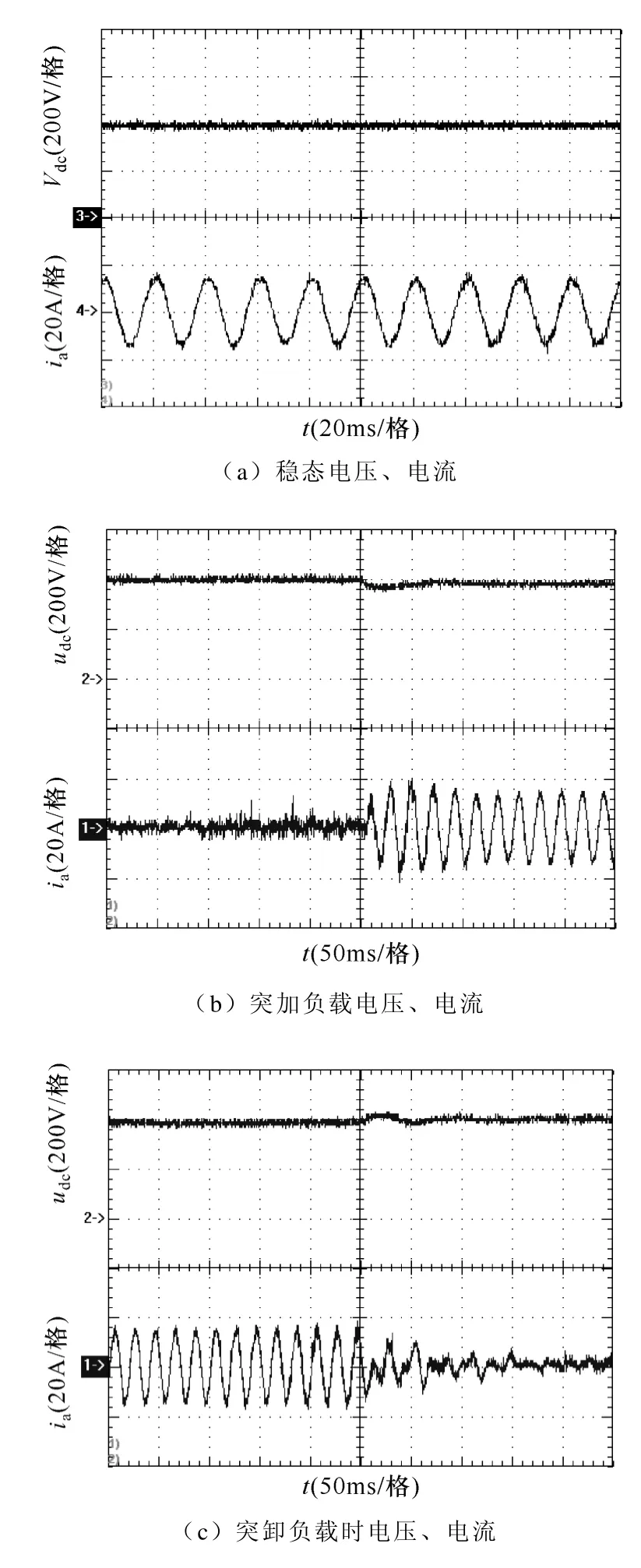
圖7 基于電壓電流平方雙閉環控制實驗波形Fig.7 Experimental waveforms of based on square of voltage-current dual-loop control

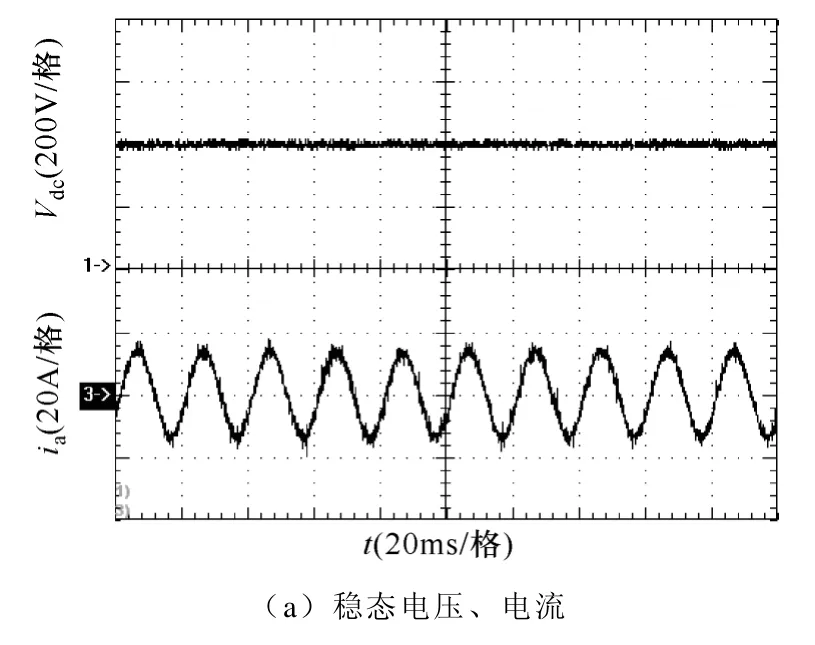
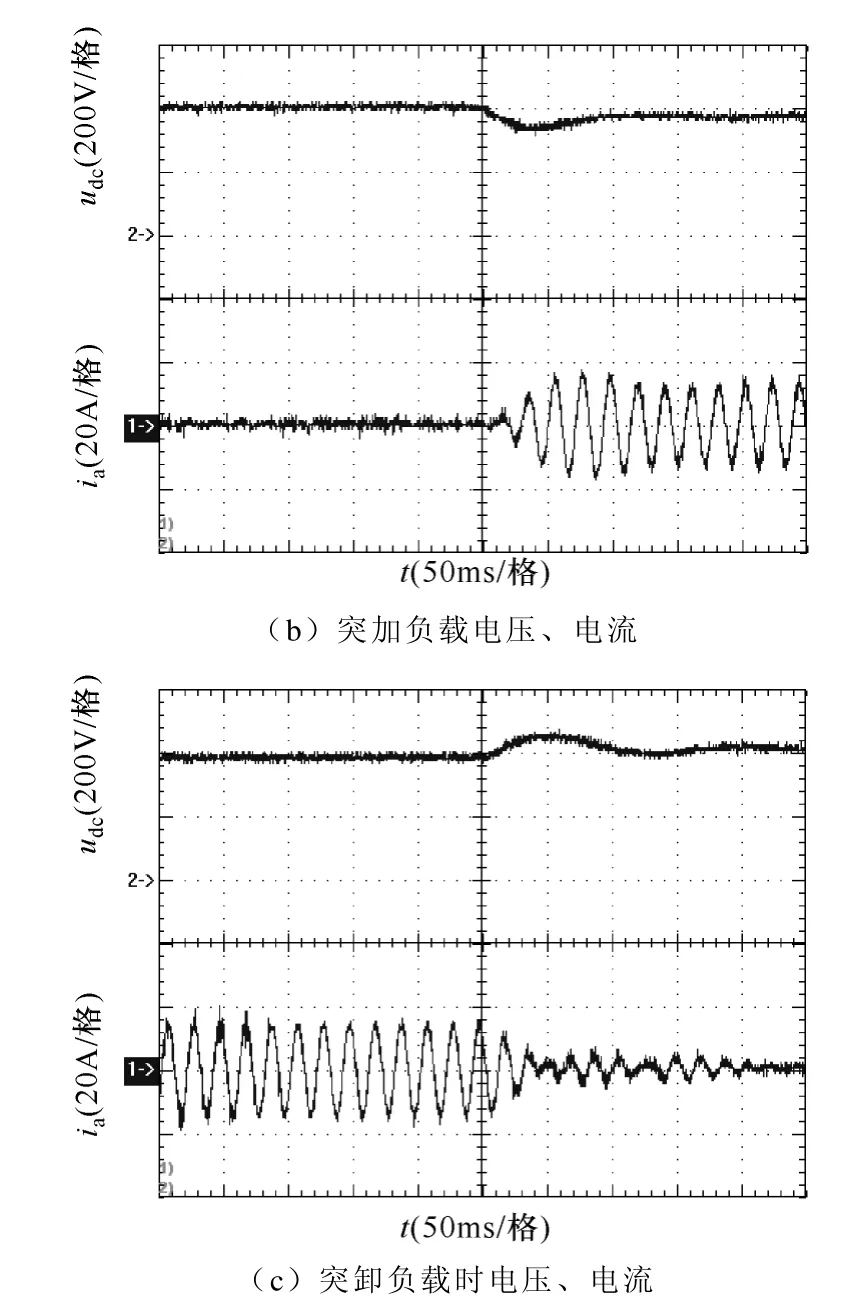
圖8 基于傳統電壓電流雙閉環控制實驗波形Fig.8 Experimental waveforms based on traditional voltage-current dual-loop control

通過比較分析實驗波形圖7 和圖8 可知:基于電壓電流平方雙閉環控制和基于傳統電壓電流雙閉環控制均能實現整流器直流側穩態電壓的零靜差控制以及交流側相電流的正弦化控制，其中前者電流穩態THD 為7.5%，功率因數計算約為0.95；后者電流穩態THD 為6.9%，功率因數計算約為0.96；但在突加滿載時，前者控制的輸出直流電壓跌落值約為10V、調節時間為40ms，后者控制的輸出電壓跌落值為50V、調節時間為80ms；突卸負載時，前者控制的輸出直流電壓超調值為15V、調整時間為50ms，后者控制的輸出直流電壓超調值約為60V、調整時間為100ms。綜上比較，基于電壓電流平方雙閉環控制策略可獲得更好的動態響應速度，并且具有更好的抗負載擾動能力。

6 結論

本文通過在對三相PWM 整流器及其傳統電壓電流雙閉環控制模型的分析研究基礎上，提出了基于電壓電流平方雙閉環控制方案，該方案具有控制結構簡單、魯棒性好等優點，可以滿足船舶電力推進系統等對于動態響應要求較高的應用場合；最后，通過仿真和實驗驗證了該控制方案的合理性與可行性。

[1]石健將,陸熙,王寶臣,等.航空 400Hz 三相高功率因數PWM 整流器的零靜差矢量控制[J].電工技術學報,2010,25(2):80-85.Shi Jianjiang,Lu Xi,Wang Baochen,et al.400Hz aeronautical three-phase PWM rectifier based on vector control with zero-static-error compensation[J].Transactions of China Electrotechnical Society,2010,25(2):80-85.

[2]翟博,呂征宇.三相電壓型 PWM 整流器小信號建模及其控制器設計[J].電工技術學報,2010,25(5):103-108.Qu Bo,Lü Zhengyu.Small-singal modeling and controller design of three-phase voltage source pwm rectifier[J].Transactions of China Electro-technical Society,2010,25(5):103-108.

[3]Shuhui Li,Timothy A Haskew,Richard P Swatloski,et al.Optimal and direct-current vector control of direct-driven PMSG wind turbines[J].IEEE Transactions on Power Electronics,2012,27(5):2325-2337.

[4]張興,張崇巍.PWM 整流器及其控制[M].北京:機械工業出版社,2012.

[5]Rusong Wu,Shashi B Dewan.Analysis of an AC/DC voltage source converter using PWM with phase and amplitude control[J].IEEE Transactions on Industrial Application,1991,27(2):355-363.

[6]張純江,顧和榮.基于新型相位幅值控制的三相PWM 整流器數學模型[J].中國電機工程學報,2003,23(7):28-31.Zhang Chunjiang,Gu Herong.Mathematical model of three-phase PWM rectifier based on a novel phase and amplitude control[J].Proceedings of the CSEE,2003,23(7):28-31.

[7]王英,張純江,陳輝明.三相PWM 整流器新型相位幅值控制數學模型及其控制策略[J].中國電機工程學報,2003,23(11):85-89.Wang Ying,Zhang Chunjiang,Chen Huiming.A new phase and amplitude control strategy and mathmatics model of three-phase voltage rectifier[J].Proceedings of the CSEE,2003,23(11):85-89.

[8]張純江,郭忠南,王芹,等.基于新型相位幅值控制的三相PWM 整流器雙向工作狀態分析[J].中國電機工程學報,2006,26(11):167-171.Zhang Chunjiang,Guo Zhongnan,Wang Qin,et al.Analysis of bi-direction operation state of three phase pwm rectifier based on a new phase and amplitude control[J].Proceedings of the CSEE,2006,26(11):167-171.

[9]Vladimir Blasko,Vikram Kaura.A new mathematical model and control of a three-phase AC-DC voltage source converter[J].IEEE Transactions on Power Electronics,1997,12(1):116-123.

[10]Sergio Vazquez,Juan Antonio Sanchez,Juan Manuel Carrasco,et al.A model-based direct power control for three-phase power converters[J].IEEE Transactions on Industrial Electronics,2008,55(4):1647-1657.

[11]Abdelouahab Bouafia,Jean-Paul Gaubert,Fateh Krim.Predictive direct power control of three phase pulsewidth modulation (PWM) rectifier using space-vector modulation (SVM)[J].IEEE Transactions on Power Electronics,2010,25(1),228-236.

[12]王久和,李華德.一種新的電壓型 PWM 整流器直接功率控制策略[J].中國電機工程學報,2005,25(16):47-52.Wang Jiuhe,Li Huade.A new direct power control strategy of thee phase boost type PWM rectifier[J].Proceedings of the CSEE,2005,25(16):47-52.

[13]王久和,李華德,王立明.電壓型 PWM 整流器直接功率控制系統[J].中國電機工程學報,2006,26(18):54-60.Wang Jiuhe,Li Huade,Wang Liming.Direct power control system of three phase boost type PWM rectifiers[J].Proceedings of the CSEE,2006,26(18):54-60.

[14]Bo Yin,Ramesh Oruganti.A simple single-inputsingle-output(SISO) model for a three-phase PWM rectifier[J].IEEE Transactions on Power Electronics,2009,24(3):620-631.

[15]倪靖猛,方宇,邢巖,等.基于優化負載電流前饋控制的400Hz 三相 PWM 航空整流器[J].電工技術學報,2011,26(2):141-146.Ni Jingmeng,Fang Yu,Xing Yan,et al.Three-phase 400Hz PWM rectifier based on optimized feed-forward control for aeronautical application[J].Transactions of China Electrotechnical Society,2011,26(2):141-146.

[16]鐘炎平,沈頌華.PWM 整流器的一種快速電流控制方法[J].中國電機工程學報,2005,25(12):52-56.Zhong Yanping,Shen Songhua.A fast current control scheme for PWM rectifier[J].Proceedings of the CSEE,2005,25(12):52-56.

[17]Tsai M T,Tsai W I.Analysis and design of threephase AC-to-DC converters with high power factor and near-optimum feed forward[J].IEEE Transactions on Industrial Electronics,1999,46(3):535-543.

[18]王成元,夏加寬,孫宜標.現代電機控制技術[M].北京:機械工業出版社,2010.

[19]徐德鴻.電力電子系統建模及控制[M].北京:機械工業出版社,2011.