一類三點邊值問題正解的存在性和唯一性

苗鳳華，宋玥薔

（1.長春師范大學數學學院，吉林長春130032；2.長春師范大學科研處，吉林長春130032；3.吉林大學符號計算與知識工程教育部重點實驗室，吉林長春130012）

一類三點邊值問題正解的存在性和唯一性

苗鳳華1，宋玥薔2，3

（1.長春師范大學數學學院，吉林長春130032；2.長春師范大學科研處，吉林長春130032；3.吉林大學符號計算與知識工程教育部重點實驗室，吉林長春130012）

研究了一類帶有遞增同胚和正同態算子的三點邊值問題，利用偏序集上的不動點定理證明了該問題正解的存在性和唯一性，并且證明了這個正解是嚴格單調遞增的.

偏序集；不動點定理；正解

本文考慮如下三點邊值問題：

其中φ是遞增同胚和正同態算子，且φ（0）＝0.

最近，具有遞增同胚和正同態算子的多點邊值問題正解的存在性和多解性越來越受到廣泛關注［13］，在假設非線性項f滿足一定的條件下，可以利用錐上的不動點定理證明正解的存在性和多解性.但是對于遞增同胚和正同態算子的三點邊值問題（1）—（2）正解的唯一性還沒有結果.為此，本文受文獻［2，4］的啟發將利用偏序集上的不動點定理來證明問題（1）—（2）正解的存在性和唯一性，并且證明這個正解是嚴格單調遞增的.

偏序集上的不動點定理以及其應用見文獻［4－8］.

1 預備知識

首先我們給出本文所要用的偏序集上的不動點定理.

定理1.1［5］設（E，≤）是一個偏序集，d是E上的一個度量使得（E，d）是一個完備的度量空間.假設E滿足下面的條件：

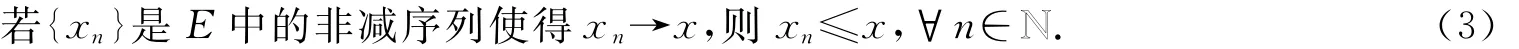
令T：E→E是一個非減映射使得

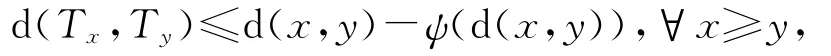
其中ψ：［0，＋∞）→［0，＋∞）是一個連續非減函數，使得ψ在（0，＋∞）上是正的，ψ（0）＝0，并且.如果存在x0∈E，并且x0≤T（x0），那么T有一個不動點.

如果我們考慮（E，≤）滿足條件：

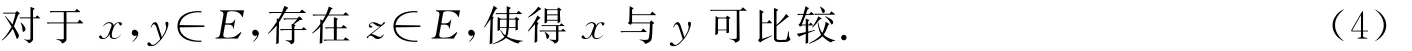
那么我們有下面的結論.

定理1.2［6］設（E，≤）是一個偏序集，d是E上的一個度量，使得（E，d）是一個完備的度量空間.假設E滿足條件（3）和（4），則不動點是唯一的.

本文所采用的基本空間是E＝C［0，1］，則E是一個實的Banach空間，其范數為注意到這個空間可以賦予偏序為x，y∈C［0，1］，x≤y?x（t）≤y（t），t∈［0，1］.在文獻［6］中證明了（C［0，1］，≤）有經典度量滿足定理1.1中的條件（3）.更進一步的，對任意的x，y∈C［0，1］，函數max｛x，y｝∈C［0，1］，（C［0，1］，≤）滿足條件（4）.

2 主要結果及其證明

定理2.1 假設下面的條件成立：

（Ⅰ）a（t）是一個非負可測函數，并且在區間［0，1］的任何一個子區間上不為零，滿足

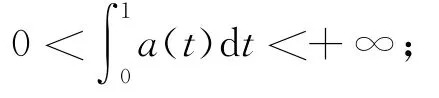
（Ⅱ）f：［0，＋∞）→［0，＋∞）是連續的，并且關于變量u是非減的；f（u（t））?0，對任意的t∈Z?［0，1］，并且μ（Z）＞0（μ為Lebesgue測度）；

則邊值問題（1）—（2）存在唯一且嚴格單調遞增的正解u（t）.

證明 首先考慮錐K＝｛u∈C［0，1］：u（t）≥0｝.則K是C［0，1］中的一個閉子集，賦予距離以后，錐K是一個完備的度量空間.

其次，考慮算子T，定義

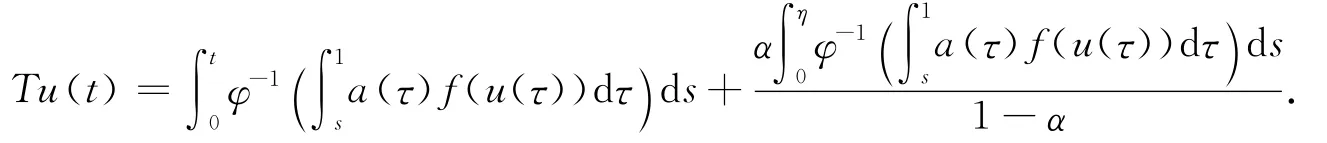
由條件（Ⅰ），（Ⅱ）可知T（K）?K.

最后，我們來證明滿足定理1.1和定理1.2所有的條件.

由條件（Ⅱ）和u≥v可知

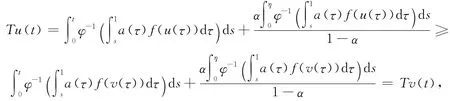
這就意味著算子T是非減的.另一方面，由條件（Ⅲ），對任意的u≥v，我們有

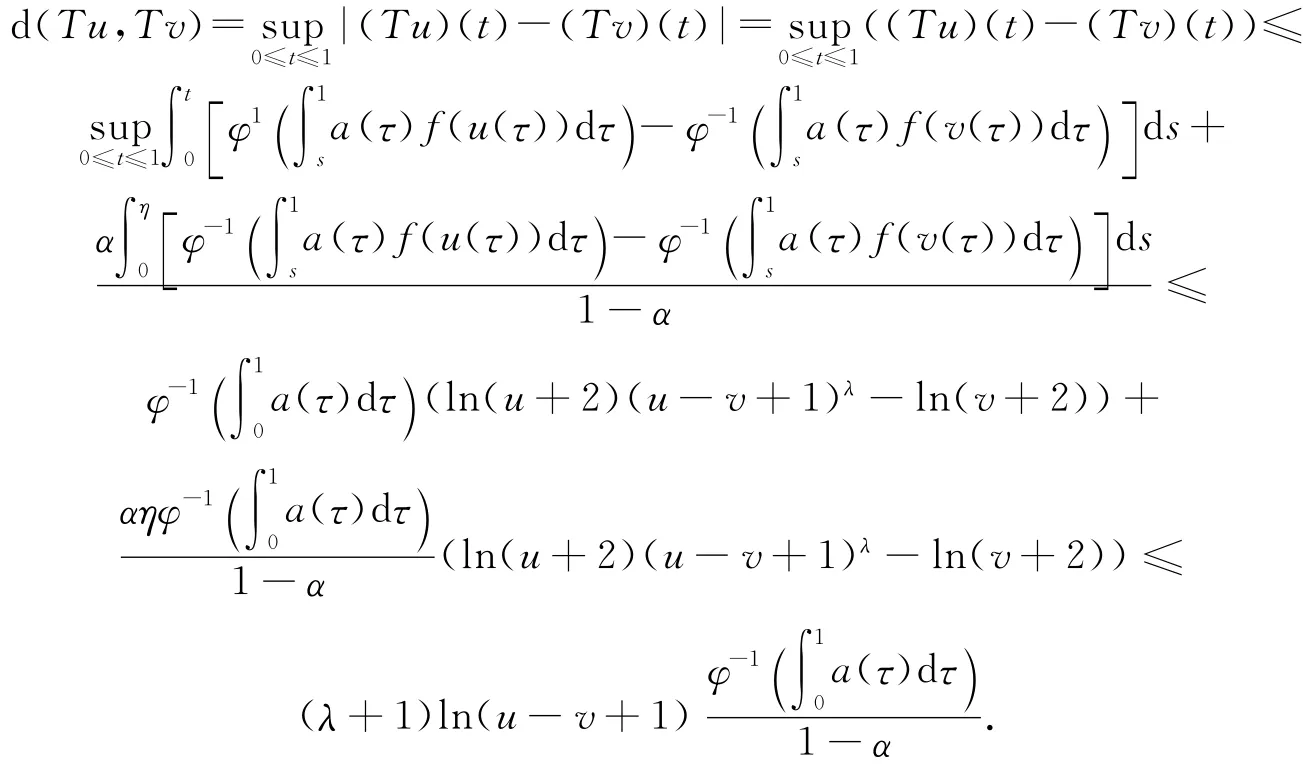
因為函數h（x）＝ln（x＋1）是非減的，又由條件（Ⅲ）可知

令ψ（x）＝x－ln（x＋1）.顯然ψ：［0，＋∞）→［0，＋∞）是連續的，非減且.則對任意的u≥v有

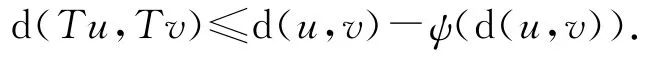
由條件（Ⅰ）和（Ⅱ）我們知道

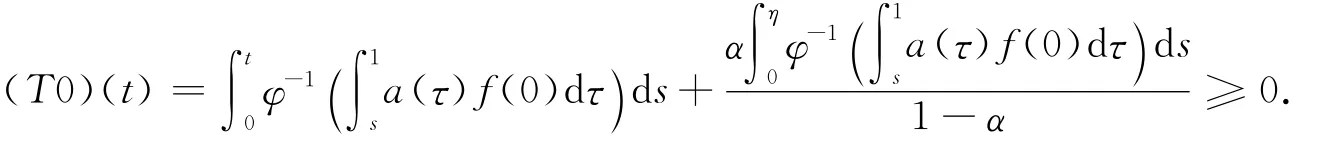
因此，由定理1.1知，邊值問題（1）—（2）至少有一個非負解.又因為（K，≤）滿足條件（4），所以，由定理1.2證明邊值問題（1）—（2）是唯一的.再由算子T的定義和條件（Ⅰ）—（Ⅱ）易證這個正解是嚴格遞增的.證畢.

［1］ LIANG S H，ZHANG J H.The existence of countably many positive solutions for nonlinear singular m－point boundary value problems［J］.J Comput Appl Math，2008，214：78－89.

［2］ LIU B F，ZHANG J H.The existence of positive solutions for some nonlinear boundary value problems with linear mixed boundary conditions［J］.J Math Anal Appl，2005，309：505－516.

［3］ LIU B F，ZHANG J H.The existence of positive solutions for some nonlinear equation systems［J］.J Math Anal Appl，2006，324：970－981.

［4］ CABALLERO MENA J，HARJANI J，SADARANGANI K.Existence and uniqueness of positive and nondecreasing solutions for a class of singular fractional boundary value problems［J］.Boundary Value Problems，2009：1－10.

［5］ HARJANI J，SADARANGANI K.Fixed point theorems for weakly contractive mappings in partially ordered sets［J］.Nonlinear Anal，2009，71：3403－3410.

［6］ NIETO J J，RODRíGUEZ－LóPEZ R.Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations［J］.Order，2005，22：223－239.

［7］ NIETO J J，RODRíGUEZ－LóPEZ R.Fixed point theorems in ordered abstract spaces［J］.Proceedings of the American Mathematical Society，2007，135：2505－2517.

［8］ REGAN D，PETRUSEL A.Fixed point theorems for generalized contractions in ordered metric spaces［J］.J Math Anal Appl，2008，341：1241－1252.

Existence and uniqueness of positive solutions to a class of three－point boundary value problem

MIAO Feng－hua1，SONG Yue－qiang2，3
（1.College of Mathematics，Changchun Normal University，Changchun 130032，China；2.Scientific Research Department，Changchun Normal University，Changchun 130032，China；3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education，Jilin University，Changchun 130012，China）

In this paper，we consider a class of three－point boundary value problem with increasing homeo－morphism and positive homomorphism.By using a fixed－point theorem in partially ordered sets，we obtain the existence and uniqueness of positive and strictly increasing solutions to the above boundary value problem.

partially ordered sets；fixed－point theorem；positive solution

O 175.14 ［學科代碼］ 110·44

A

（責任編輯：陶 理）

1000－1832（2014）02－0009－03

10.11672／dbsdzk2014－02－002

2013－05－13

吉林省自然科學青年基金資助項目（20130522100JH）；吉林省教育廳“十二五”科學技術研究項目（吉教科合字2013第252號）；教育部重點實驗室開放課題項目（93K172013K03）；長春師范學院自然科學基金資助項目（2011第02號）.

苗鳳華（1968—），女，碩士研究生，副教授，主要從事非線性微分方程理論及應用研究.