偏差依賴于未知函數(shù)的高階泛函微分方程的振動(dòng)定理
林丹玲
(韓山師范學(xué)院數(shù)學(xué)與應(yīng)用數(shù)學(xué)系,廣東潮州521041)
偏差依賴于未知函數(shù)的高階泛函微分方程的振動(dòng)定理
林丹玲
(韓山師范學(xué)院數(shù)學(xué)與應(yīng)用數(shù)學(xué)系,廣東潮州521041)
考慮高階泛函微分方程
建立其一切有界解振動(dòng)的充分條件,推廣和改進(jìn)了已有工作中的相應(yīng)結(jié)果,其中n≥2,偏差變?cè)(j=1,2,…,k)依賴于獨(dú)立變量t和未知函數(shù)x.
高階微分方程;時(shí)滯依賴未知函數(shù);有界解;振動(dòng)
1 預(yù)備知識(shí)
考慮時(shí)滯依賴于未知函數(shù)的高階泛函微分方程
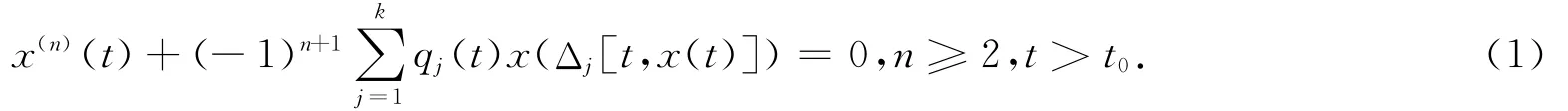
其中偏差變?cè)(j=1,2,…,k)依賴于獨(dú)立變量t和未知函數(shù)x.假設(shè)下列條件對(duì)j=1,2,…,k成立:(A1)qj(t)∈C([t0,∞),R+),t0>0,R+=[0,∞),且存在j0∈{1,2,…,k},使得qj0(t)>0,t≥t0;(A2)Δj[t,u]∈C([t0,∞)×R,R),且對(duì)于每一固定的滿足|u|≤D(D為正常數(shù))的u,有Δj[t,u]<t,且
(A3)Δj[t,u1]≤Δj[t,u2],當(dāng)u1≤u2<0時(shí);Δj[t,u1]≥Δj[t,u2],當(dāng)0<u1≤u2時(shí);且Δj[t1,u]≤Δj[t2,u],當(dāng)0≤t1≤t2時(shí).
定義1[1]實(shí)值函數(shù)φ(t)稱為方程(1)的解,如果它在[t0,∞)上定義,有n階導(dǎo)數(shù)并且滿足下列條件:
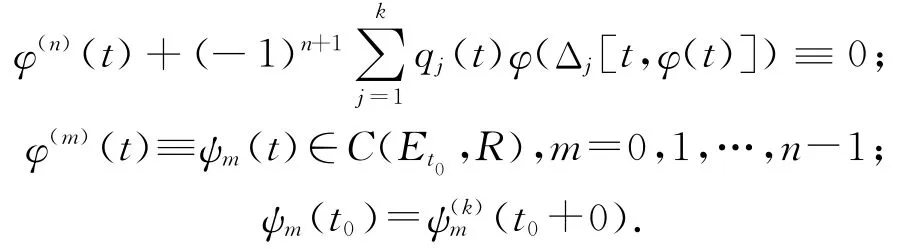
其中ψm(t)是定義在初始集合
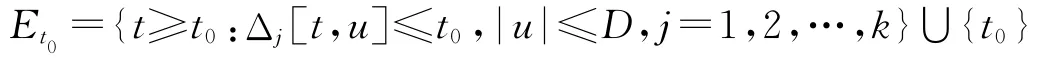
上的函數(shù).本文考慮方程(1)的解集
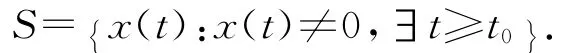
我們假設(shè)函數(shù)qj(t)和Δj[t,u]使得方程(1)存在屬于S的解.
定義2 方程(1)的解稱為振動(dòng)的,如果它有任意大的零點(diǎn);否則稱它為非振動(dòng)的.
近年來泛函微分方程解的振動(dòng)性研究取得了豐碩成果[1-6],但其中大多數(shù)結(jié)果對(duì)偏差變?cè)獌H依賴于時(shí)間t.我們注意到偏差變?cè)瑫r(shí)依賴于狀態(tài)x(t)和時(shí)間t的方程在理論上和實(shí)際應(yīng)用中有重要意義.然而目前文獻(xiàn)中此類方程的振動(dòng)結(jié)果還不很多[7-14],已有工作中主要是關(guān)于一階和二階方程解的振動(dòng)性和漸近性的研究,而對(duì)一般高階方程的振動(dòng)定理尚未見到.本文的目的是給出高階方程(1)的一切有界解的振動(dòng)定理.
當(dāng)方程(1)中偏差變?cè)(j=1,2,…,k)不依賴x(t)時(shí),有如下重要特例:
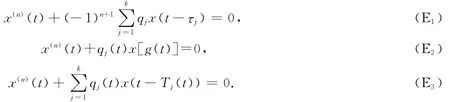
G.Ladas等人在文獻(xiàn)[15]中證明了當(dāng)k=1時(shí),方程(E1)的一切有界解振動(dòng)的必要充分條件是
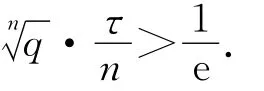
文獻(xiàn)[3]給出,若n為奇數(shù),q(t)>0且g(t)≤t非減,則方程(E2)的每一解振動(dòng)的充分條件是
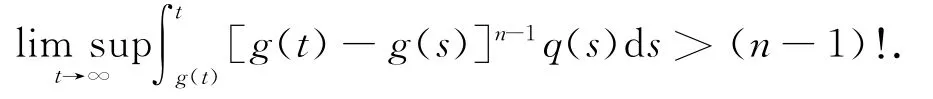
最近,文獻(xiàn)[16]證明了,若n為奇數(shù),qj(t)>0且Tj(t)>0,j=1,2,…,k,則方程(E3)的每一解振動(dòng)的充分條件是
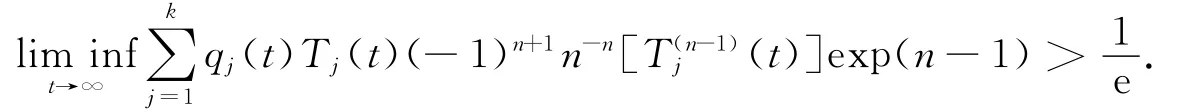
本文得到的結(jié)果不僅適用于n為奇數(shù),而且也適用于n為偶數(shù),因此,它部分地推廣和改進(jìn)了文獻(xiàn)[3,15-16]中的有關(guān)結(jié)果.
2 主要結(jié)果
為證明本文的定理,我們需要下面兩個(gè)引理.
引理1[3]設(shè)y(t)是R+上的n次可微函數(shù)且具有常號(hào),?t≥0,使得y(n)(t)≠0,在[t1,∞)上滿足y(n)(t)y(t)≤0,則:
(ⅰ)存在t2≥t1,使得函數(shù)y(j)(t)(j=1,2,…,n-1)在區(qū)間[t2,∞)上常號(hào).
(ⅱ)存在整數(shù)l,0≤l≤n-1,當(dāng)n為偶數(shù)時(shí),l為奇數(shù);當(dāng)n奇數(shù)時(shí),l為偶數(shù).使得
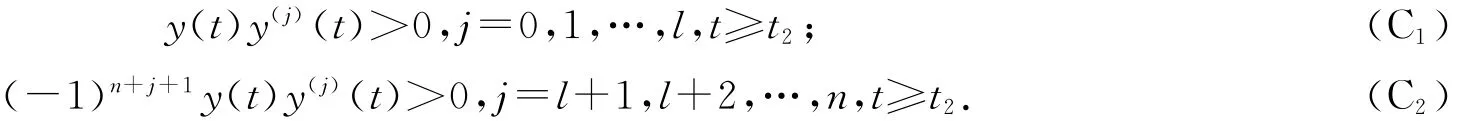
引理2[3]設(shè)y,y′,…,y(n-1)在區(qū)間(t0,∞)上絕對(duì)連續(xù)且常號(hào),若y(n)(t)y(t)≥0,則下列結(jié)論之一成立:
(ⅰ)y(t)y(j)(t)≥0,j=0,1,…,n.
(ⅱ)存在整數(shù)l,0≤l≤n-2,當(dāng)n為偶數(shù)時(shí),l為偶數(shù);當(dāng)n奇數(shù)時(shí),l為奇數(shù).使得
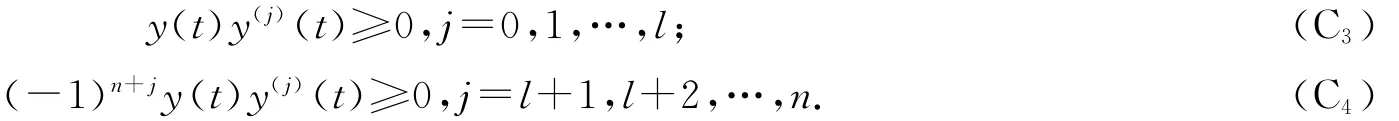
本文主要結(jié)果為下述定理.
定理1 設(shè)條件(A1),(A2)和(A3)成立.若對(duì)每一固定的u(|u|≤D),有
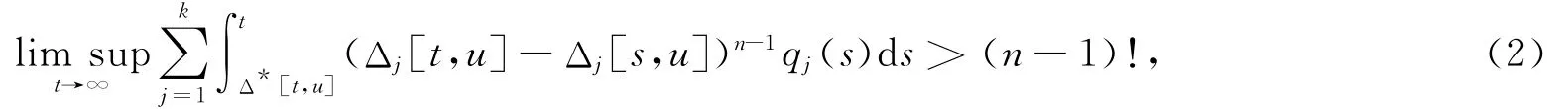
證明 設(shè)方程(1)存在有界非振動(dòng)解x(t),不失一般性,不妨設(shè)x(t)>0,t≥t1≥t0.由條件(A2)和(A3),存在t2≥t1,使得
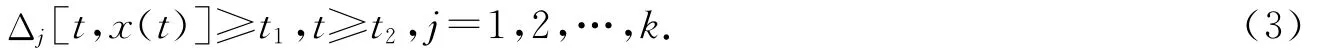
方程(1)可寫為
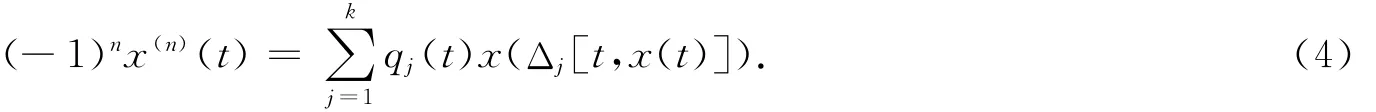
注意到條件(A1),(A3),(3)式和x(t)>0,我們有

因此,存在t3≥t2,使得當(dāng)t≥t3時(shí),x(j)(t)定號(hào),j=0,1,…,n-1.
先令n為偶數(shù),則x(n)(t)>0.故由引理2,存在t4≥t3和偶數(shù)l使得(C3)和(C4)式對(duì)t≥t4成立.
首先,設(shè)l≥2,則x″(t)>0,t≥t4.故x′(t)單調(diào)非減.又因x′(t)>0,此與x(t)的有界性矛盾.因此,l=0,故有
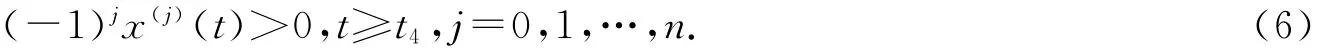
對(duì)任意u和v(u≤v)應(yīng)用Taylor公式,注意到(6)式,我們得到
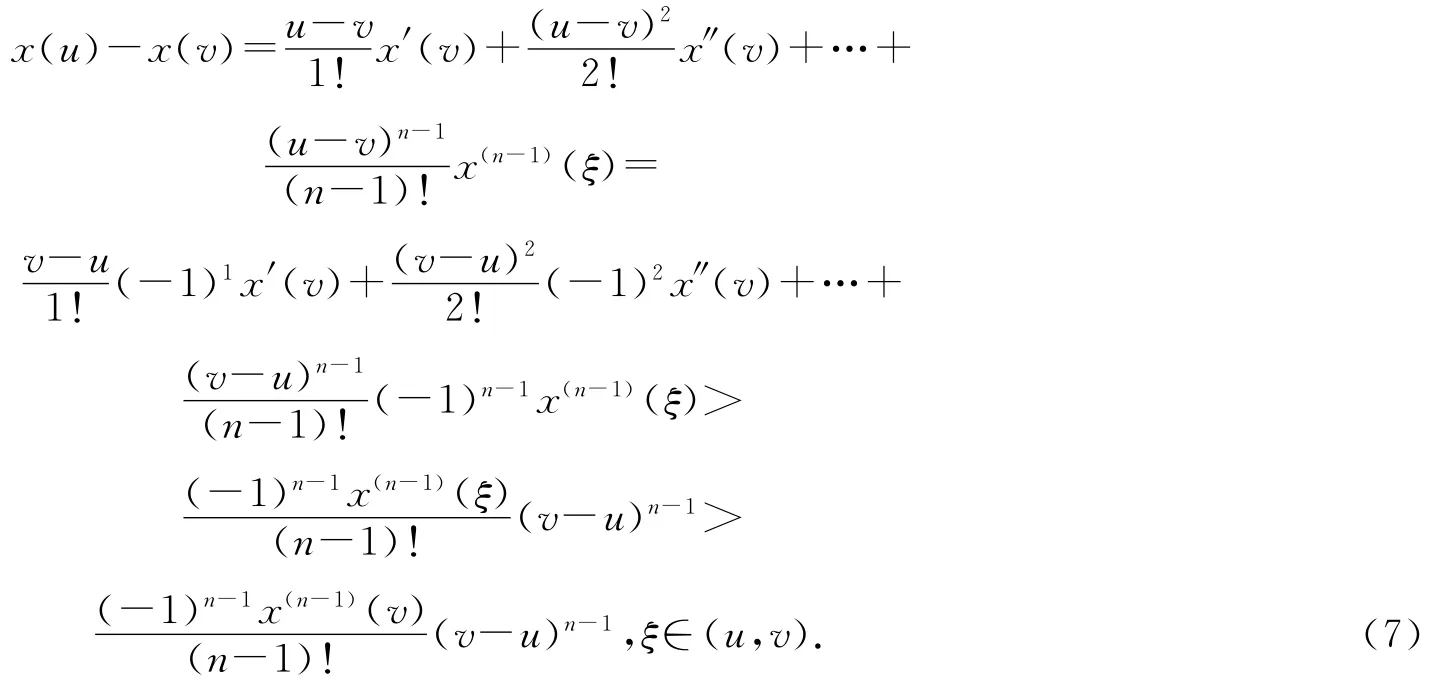
從條件(A2),(A3)和(7)式可以看出,存在t5≥t4,使得對(duì)于t≥s≥t5,有
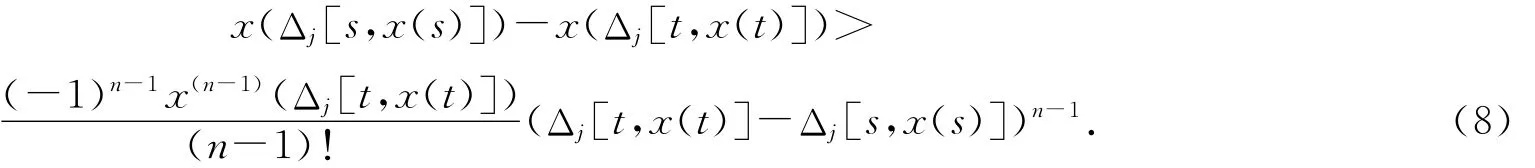
用qj(s)乘(8)式,并對(duì)j從1到k求和,注意到條件(A3),得到
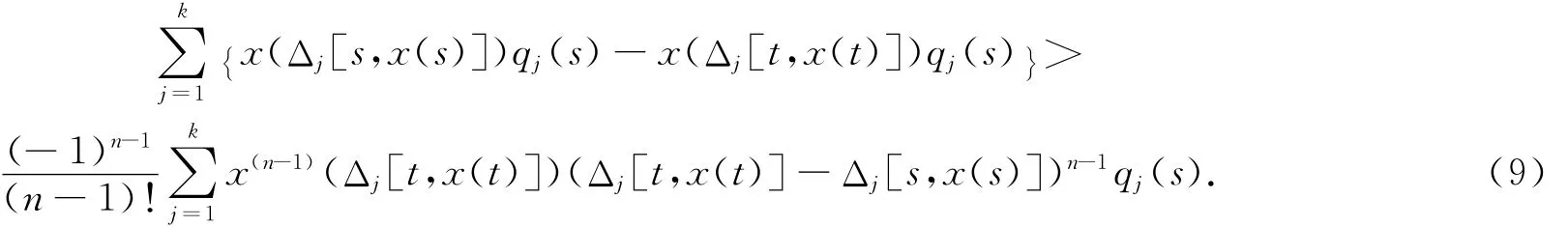
利用(4)和(9)式,并注意到n為偶數(shù),有
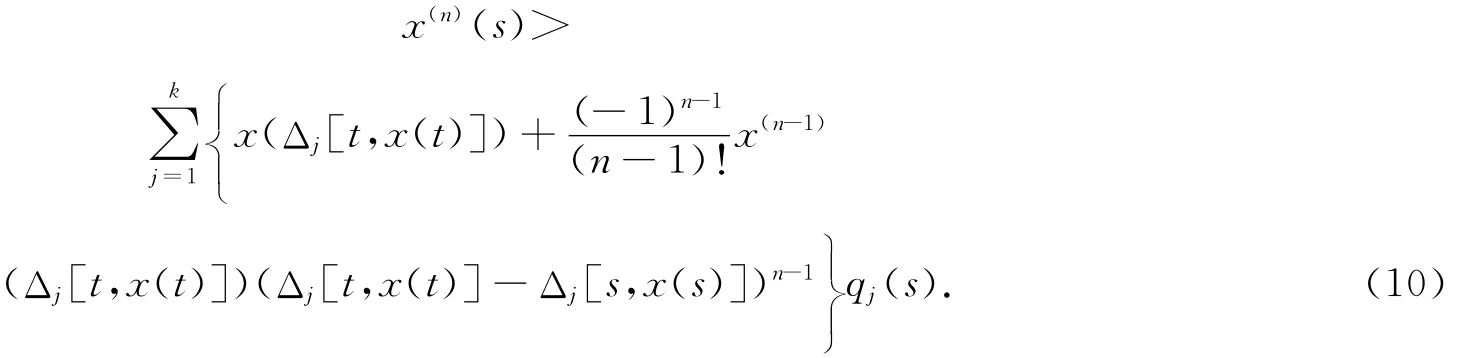
從Δ*[t,x(t)]到t關(guān)于s對(duì)(10)式積分,得
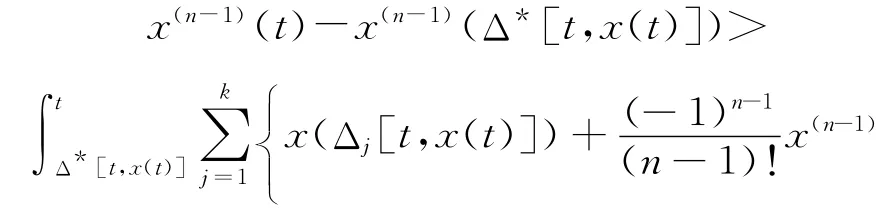
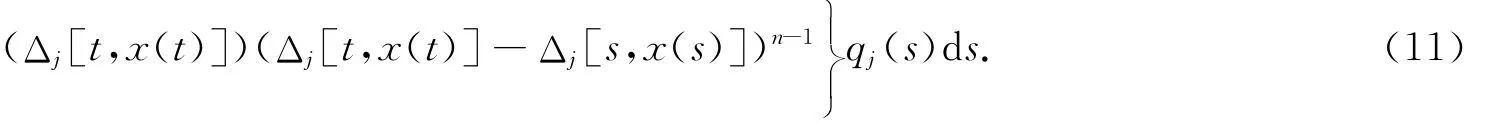
由不等式(5)知,x(n-1)(t)非減.注意到Δ*[t,x(t)]的定義,得到
因此,我們有
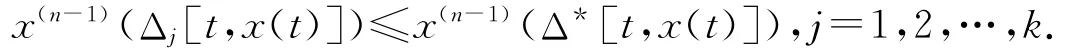
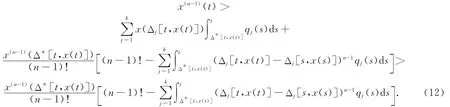
考慮到條件(A3)和表達(dá)式(Δj[t,x(t)]-Δj[s,x(s)])n-1中解出x(t)是正的,我們得到如下估計(jì):
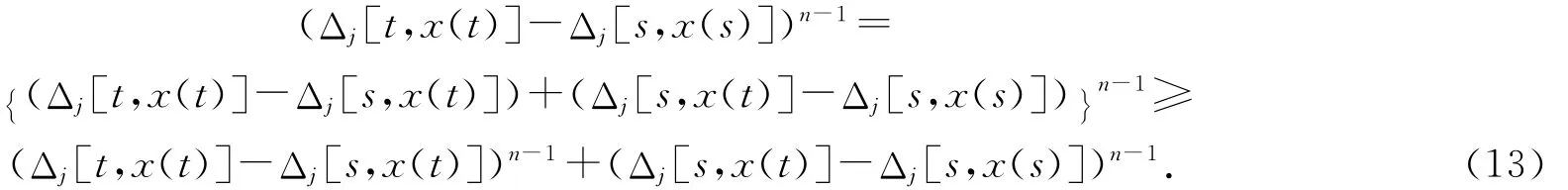
利用條件(2)和(13),有
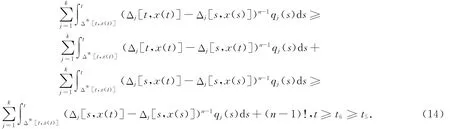
在(14)式中因x(t)非減,并滿足條件(A3),可重寫為
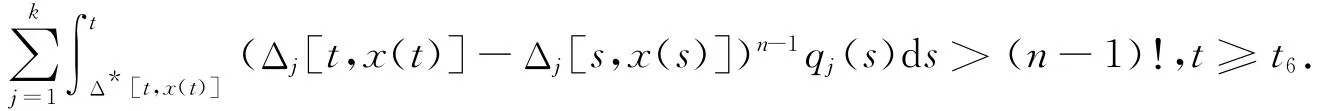
上式等價(jià)于
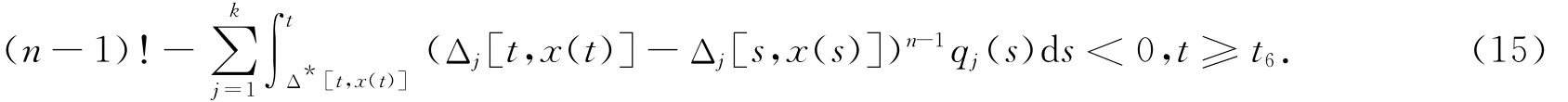
在(6)式中令j=n-1,得到

注意到(15)和(16)式,由(12)式產(chǎn)生

(17)式與(6)式矛盾.因此,當(dāng)n為偶數(shù)時(shí),方程(1)的每一有界解振動(dòng).
其次,設(shè)n為奇數(shù),則由方程(1)我們得到x(n)(t)<0.故由引理1,存在t2≥t1和偶數(shù)l使得(C1)和(C2)對(duì)t≥t2成立.如同n為偶數(shù)的情況一樣,設(shè)l≥2,則由(C1)式得x(j)(t)>0,j=0,1,2.這與x(t)的有界性矛盾,因此l=0.由(C2)式,我們有

顯然,(18)式即為(6)式.應(yīng)用Taylor公式和(6)式,同樣得到(7)式.因n為奇數(shù),故(-1)n-1=1.于是,(7)式成為
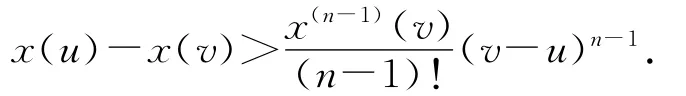
接下來的討論與n為偶數(shù)的情況一樣.我們可以得到x(n-1)(t)<0.但此與(18)式矛盾.因此,當(dāng)n為奇
數(shù)時(shí),方程(1)的有界解均振動(dòng).定理證畢.例1 考慮二階方程
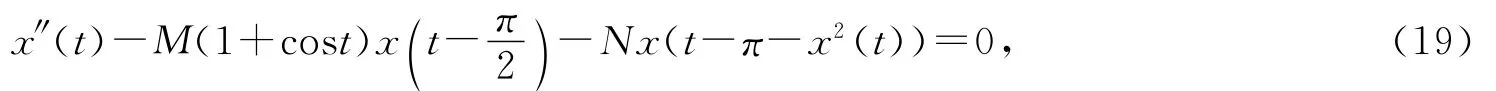
其中M和N為正常數(shù)且滿足條件

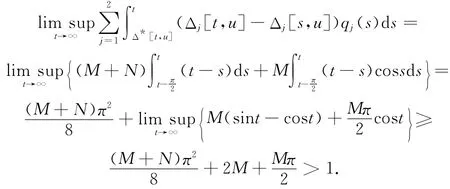
因此,根據(jù)定理1,方程(19)的每一有界解振動(dòng).
例2 考慮三階方程

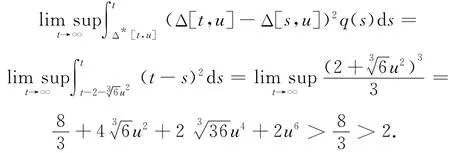
因此,根據(jù)定理1,方程(21)的每一有界解振動(dòng).
[1] SHEVELOV N.Oscillation of solutions of differential equations with deviating arguments[M].Kiev:Science Press,1978:46-79.
[2] AGARWAL R P,GRACE S R,O'REGAN D.Oscillation theory for second order dynamic equations[M].U K:Taylor &Francis,2003:35-184.
[3] ERBE L H,KONG Q,ZHANG B.Oscillation theory for functional differential equations[M].New York:Marcel Dedder,1995:288-373.
[4] GYORY I,LADAS G.Oscillation theory of delay differential equations with applications[M].Oxford:Clarendon Press,1991:32-57.
[5] LADAS G,LAKSHMIKANTHAM V,ZHANG B.Oscillation theory of differential equations with deviating arguments[M].New York:Marcel Dedder,1987:70-124.
[6] AGARWAL R P,GRACE S R,O'REGAN D.Oscillation theory for difference and functional differential equations[M].Dordrecht:Kluwer,2000:56-108.
[7] BAINOV D,SIMEONOV P.Positive solutions of a superlinear first order differential equations with delay depending on the unknown function[J].J Comput Appl Math,1998,88(1):95-101.
[8] BAINOV D,MARKOVA N,SIMEONOV P.Asymptotic behavior of the nonoscillatory solutions of differential equations of second order with delay depending on the unknown function[J].J Comput Appl Math,1998,91(1):87-96.
[9] DOMOSHNITSKY A,DRAKHLIN M,LITSYN E.On equations of second order with delay depending on solution[J].Nonl Anal,2002,49(5):689-701.
[10] HARTUNG F,TURI J.On the asymptotic behavior of the solutions of a state dependent delay equation[J].Differential and Integral Equations,1995,8:1867-1872.
[11] LI W,ZHANG S.Classifications and existence of positive solutions of higher order nonlinear iterative functional differential equations[J].J Comput Appl Math,2002,139(2):351-367.
[12] LI WANGTONG,DONG ZHONGQI.Classifications and existence of positive solutions of second order nonlinear differential equations with delay depending on the unknown functions[J].Acta Math Sci,2004,24B:403-411.
[13] LUO JIAOWAN.Asymptotic behavior of solutions of second order quasilinear differential equations with delay depending on the unknown function[J].J Comput Appl Math,2006,185(1):133-143.
[14] XU ZHITING.Oscillation and nonoscillation of second order differential equations with delay depending on the unknown function[J].J Comput Appl Math,2008,214(2):371-380.
[15] LADAS G,SFICAS Y G,STAVROULAKIS I P.Necessary and sufficient conditions for oscillation of higher order delay differential equations[J].Trans Amer Math Soc,1984,285:81-90.
[16] EL-ATTAR M A,EL-ABAD E M,EL-ABAD E E.Oscillations of the solutions of retarded differential equations[J].J Fuaay Math,2006,14:451-459.
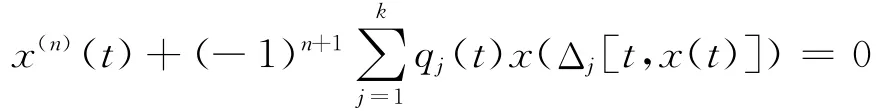
are considered,where n≥2and the deviating argumentsΔj(j=1,2,…,k)depend on the independent variable t as well as on the unknown function x.Sufficient conditions are found under which every bounded solution of the above-mentioned equation is oscillatory.
Oscillation theorem of higher order functional differential equations with deviating arguments depending on the unknown function
LIN Dan-ling
(Department of Mathematics and Applied Mathematics,Hanshan Normal University,Chaozhou 521041,China)
higher order differential equation;delay depending on the unknown function;bounded solution;oscillation
In this paper higher order functional differential equations of the type
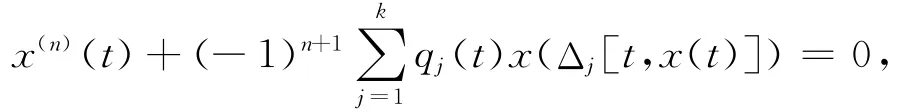
O 175 [學(xué)科代碼] 110·47
A
(責(zé)任編輯:陶 理)
1000-1832(2014)02-0016-06
10.11672/dbsdzk2014-02-004
2013-03-02
國(guó)家自然科學(xué)基金資助項(xiàng)目(11247310);韓山師范學(xué)院科研基金資助項(xiàng)目(LY201302).
林丹玲(1963—),女,副教授,主要從事泛函微分方程研究.

