等變η形式正則性的新證明
李 琦
(渤海大學數理學院,遼寧錦州121013)
等變η形式正則性的新證明
李 琦
(渤海大學數理學院,遼寧錦州121013)
將等變η形式的定義推廣至較一般的緊纖維叢沿纖維方向Clifford代數叢的自伴Clifford模上,給出了一個關于其正則性的新證明.由于將原有定義中纖維奇數的條件推廣至任意維數,因而得到更一般的結果.
等變η形式;正則性;等變指標定理
1989年,關于纖維附帶Spin結構的緊纖維叢,在沿纖維方向的狄拉克算子可逆的條件下,J-M.Bismut與J.Cheeger定義了一個底空間上的微分形式?η,并稱之為η形式[1].在纖維為偶數維的條件下,η形式可以看做此纖維叢族指標的某個超度.在文獻[2]中,戴先哲教授去掉了定義中沿纖維方向的狄拉克算子可逆的條件.緊接著,N.Berline等人將Spin條件推廣到沿纖維方向Clifford代數叢的自伴Clifford模上,并對纖維叢族指標的超度進行了研究[3].最近王勇教授對沿Spin奇數維纖維有緊李群作用的緊纖維叢定義了等變η形式,并證明了其正則性[4].本文的目的即在于沿著文獻[3]的思想,將等變η形式的定義推廣至較一般的緊纖維叢,并給出了一個關于其正則性的新證明.
1 等變η形式
設π:M→B是一個底空間為緊流形B,纖維為緊流形X的纖維叢,(TX,ɡM/B)為其相對切叢,(ε,ɡε)為相對于Clifford代數叢c(T X)的自伴Clifford模,PTX為從TM到TX的正交投影.設THM為TX在TM中的補子叢.記{fp,fq,fr,…},{ei,ej,ek,…}與{ea,eb,ec,…}分別為TB,TX與TM的局部正交基,則{,…}為THM的局部正交基.設TM,TB分別為(M,ɡTM)與(B,ɡTB)上的Levicivita聯絡,則ΔTX=PTXΔTMPTX為TX上的聯絡,S=ΔTM-π*ΔTB⊕ΔTX為第二基本形式.設ε為ε上保度量的Clifford聯絡.我們在TM上定義退化的Clifford代數叢m(TM)如下:

其中fp,H與ei分別為fHp與ei的對偶.由以上記號,作用在Γ(M,π*Λ*T*B?ε)上的Bismut超聯絡可記為
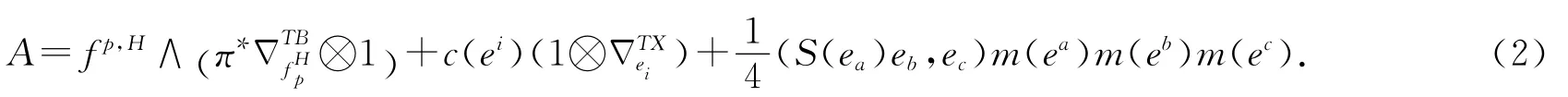
記

假設存在緊李群G作用在M上,并保持纖維不變且此群作用可提升至叢ε上,與聯絡Δε可換.不失一般性,我們假設G等距作用在M上.
定義Treven為B上所有偶形式的跡[4],那么對于任意維數的纖維,記n=dimX,我們可以定義

其中Trs為超跡,而且α∈Ωp(B).
設DX為沿纖維方向的狄拉克算子,本文假設ker DX為B上的向量叢.
定義1 對于任意ɡ∈G,假設ker DX為B上的向量叢,我們定義等變η形式為B上的微分形式
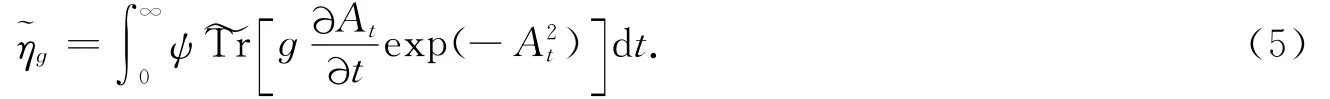
注記 當纖維為奇數維Spin流形,且ε為纖維的Spinor時,定義與文獻[4]一致.
需要注意的是,上述積分在t→0與t→+∞時的收斂性并不顯然.也就是說到目前為止,此定義是否為良好定義仍有待商榷.本文即對此積分的收斂性(正則性)加以證明,從而指出其為合理定義.
在實際應用中,最常見的非Spin結構的自伴Clifford模結構即為Spinc結構.此時Spinc結構對應的Spinor即為一個自伴Clifford模.鑒于任意復向量叢與近復流形均具有Spinc結構,故本文的推廣更具一般性.
2 等變η形式的正則性
對于定義1中的積分項,當t→+∞時,
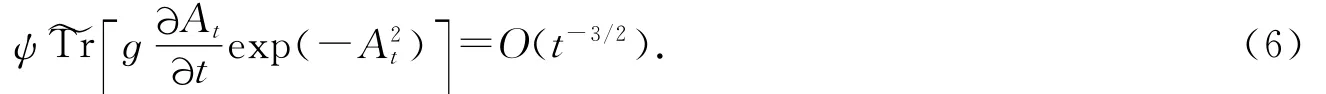
參見文獻[3]定理9.23,故只需對積分項在t→0處的正則性進行研究.
定理1 當t→0時,
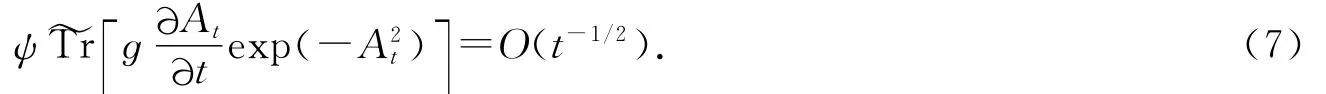
證明 設R+=(0,+∞),考慮一個新的纖維叢?π:?M=M×R+→?B=B×R+,纖維?X=X.設新纖維叢相對切叢的度量為ɡ?M/?B=s-1ɡM/B,新聯絡為原聯絡與R+方向平凡聯絡的組合,新Clifford模為?ε=ε×R+,Clifford聯絡為Δ?ε=Δε+dR+.由文獻[3]的引理10.33可知,新纖維叢上的Bismut超聯絡為

因此

對?A應用局部族指標定理,因為ɡ與As可交換,可知當t→0時,根據Duhamel原理,
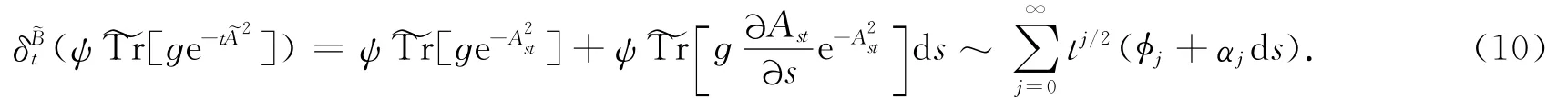
令s=1,則
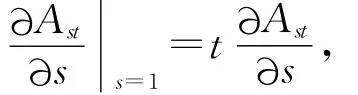
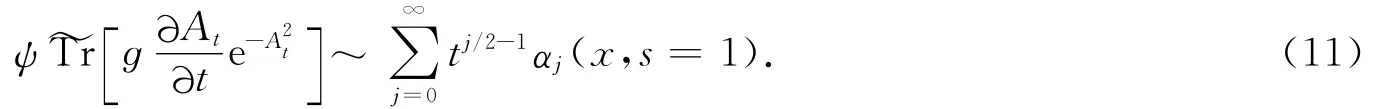
設?Xɡ為?X關于ɡ的不動點集,定義
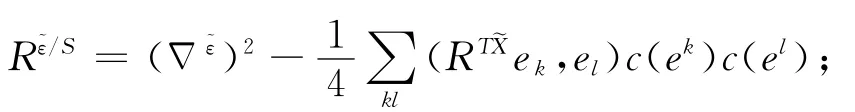
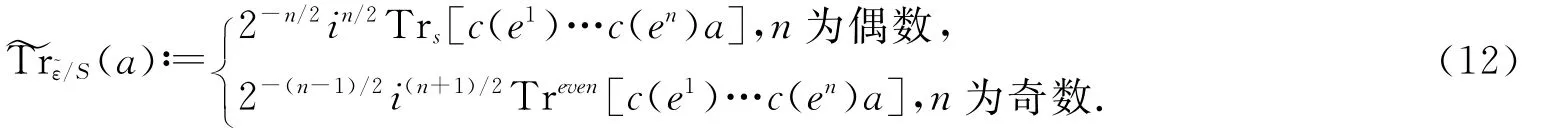
其中a∈Γ(?M,Endc(T*?X)?ε).由等變族指標定理(纖維偶數維時參見文獻[5]的定理1.3,奇數維時應用文獻[6]的定理2.10技巧化為偶數維),有
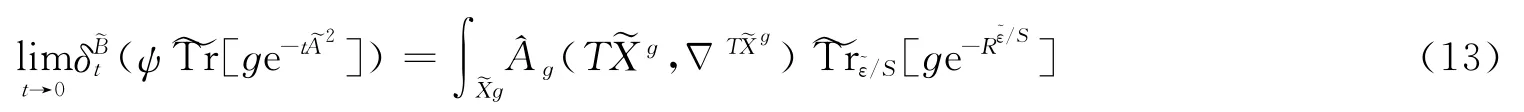
與ds無關,故α0=0.定理得證.
在無緊李群作用時,本文研究的η形式出現在最新數學領域微分K理論中,作為微分K群等價關系的一部分,在微分K理論的幾何模型中起到了關鍵的作用,并可以用來描述理論物理交換場論中場的量子奇異性.從此角度分析,由物理學中的對稱性出發,帶緊李群作用的微分K理論將會在交換場論中有更深刻的應用,而我們給出的等變η形式的良好定義,將是研究等變微分K理論幾何構造的第一步.另一方面,η形式在某種程度上可以看做Arakelov幾何中全純解析撓率的實域對應.等變η形式研究的深入必將對等變全純解析撓率的研究產生影響,并且能夠加深對算術代數幾何中算術黎曼洛赫定理的理解.
致謝:東北師范大學王勇教授對本文給予了幫助,在此表示衷心感謝!
[1] BISMUT J-M,CHEEGER J.Eta invariants and their adiabatic limits[J].J Amer Math Soc,1989,2(1):33-70.
[2] DAI X.Adiabatic imits,nonmultiplicativity of signature,and Leray spectral sequence[J].J Amer Math Soc,1991,4(2):265-321.
[3] BERLINE N,GETZLER E,VERGNE M.Heat kernels and Dirac operators[M].Berlin:Springer-Verlag,2004:1-368.
[4] WANG Y.A note on equivariant eta forms[J/OL].www.Arxiv.org.Arxiv:110.5013.
[5] LIU K,MA X.On family rigidity theorems[J].Duke Math J,2000,102(3):451-474.
[6] BISMUT J-M,FREED D.The analysis of elliptic familiesⅡdirac operators,eta invariants,and the holonomy theorem[J].Comm Math Phys,1986,107(1):103-163.
A new proof of the regularity of equivariant eta form
LI Qi
(School of Mathematics and Physics,Bohai University,Jinzhou 121013,China)
The author extends the definition of the equivariant eta form to the more general case and gives a new proof of the regularity.In this new definition,the author removes the condition odd dimensional fiber in the reference.
equivariant eta form;regularity;equivariant index theorem
O 186.16 [學科代碼] 110·27
A
(責任編輯:陶 理)
1000-1832(2014)02-0022-03
10.11672/dbsdzk2014-02-005
2013-11-02
霍英東教育基金資助項目(121003).
李琦(1963—),女,副教授,主要從事微分幾何、代數研究.

