基于Backstepping方法對超混沌Rossler系統的控制與同步研究

王 石，楊 吉，欒紅霞

（1.東北師范大學信息化管理與規劃辦公室，吉林長春130024；2.空軍航空大學基礎部，吉林長春130022；

3.東北師范大學物理學院，吉林長春130024）

基于Backstepping方法對超混沌Rossler系統的控制與同步研究

王 石1，楊 吉2，欒紅霞3

（1.東北師范大學信息化管理與規劃辦公室，吉林長春130024；2.空軍航空大學基礎部，吉林長春130022；

3.東北師范大學物理學院，吉林長春130024）

對超混沌Rossler系統提出了基于Backstepping的超混沌控制與同步方法，在反向遞推每一步設計算法中構造虛擬控制器，使得構造的Lyapunov函數導數負定，逐步修正算法使誤差系統在Lyapunov意義下漸近穩定，實現控制器的設計.只使用一個控制器實現了對超混沌Rossler系統控制與同步，數值實驗結果證實了所設計控制器的有效性.

控制；同步；Backstepping方法；超混沌Rossler系統

混沌的控制與同步在生物醫學、化學反應及保密通訊等領域應用受到了極大的關注，近些年來得到了蓬勃發展.人們提出了許多混沌控制與同步的方法［1－11］，Yassen等提出了利用Backstepping方法對嚴格反饋混沌系統實現混沌同步與控制，它是一種構造Lyapunov函數的系統方法，基于Lyapunov穩定性理論，將復雜系統分解成不超過系統階數的子系統，在反向遞推設計中構造虛擬控制器，逐步修正算法使誤差系統在Lyapunov意義下漸近穩定，完成了控制器的設計［8－11］.以上設計主要針對一般混沌系統，而超混沌系統具有2個或2個以上正的Lyapunov指數，增大了系統的隨機性和不可預測性，它在保密通信領域中具有更大的應用潛力，本文利用Backstepping方法只需要一個控制器實現對五階超混沌Rossler系統的控制和同步，數值仿真結果表明了該方法的有效性.

1 超混沌Rossler系統

超混沌Rossler系統的動力學方程［12］：

其中f（x4）＝2b（x4－d）H（x4－d），H（x4－d）是單位階躍函數，當H（x4－d≥0）＝1，H（x4－d＜0）＝0.系統（1）中：x1，x2，x3，x4，x5為系統的狀態變量；a，b，c，d為系統的參數.當參數a＝0.3，b＝4，c＝1，d＝2時，采用四階Runge－Kutta法得到超混沌Rossler系統的Lyapunov指數譜及吸引子如圖1所示.

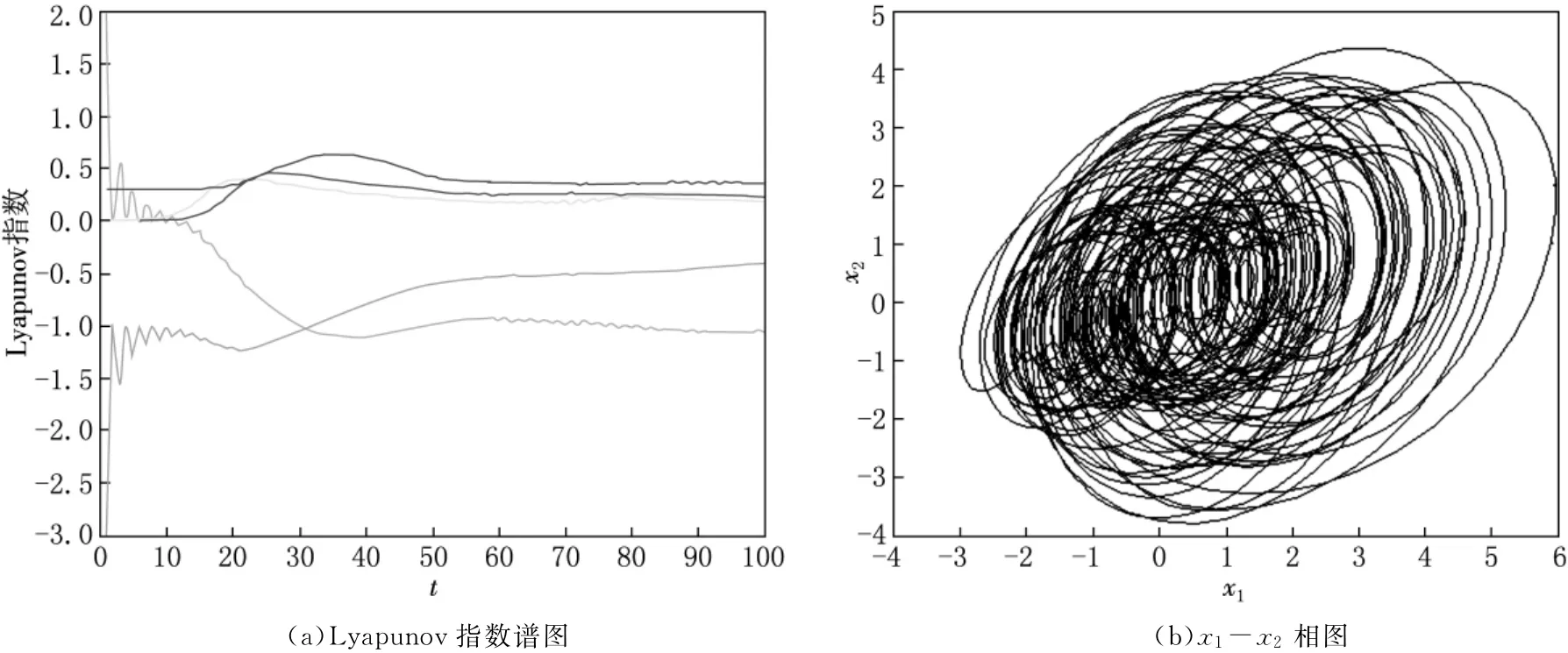
圖1 超混沌Rossler系統的Lyapunov指數譜圖和吸引子相圖

2 超混沌Rossler系統控制器的設計

對超混沌Rossler系統（1）加一個控制器u，則系統方程變為

利用Backstepping方法設計控制器u使系統（2）穩定到一有界點.選取Lyapunov函數

則有

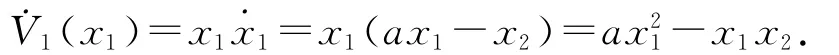
取虛擬函數α1（x1）＝（a＋1）x1.

定義誤差變量

得到（x1，ˉx2）的子系統為

選擇

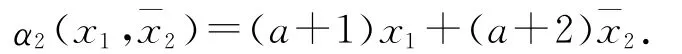
定義誤差變量

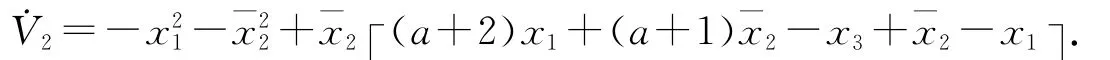
得到（x1，ˉx2，ˉx3）的子系統為：

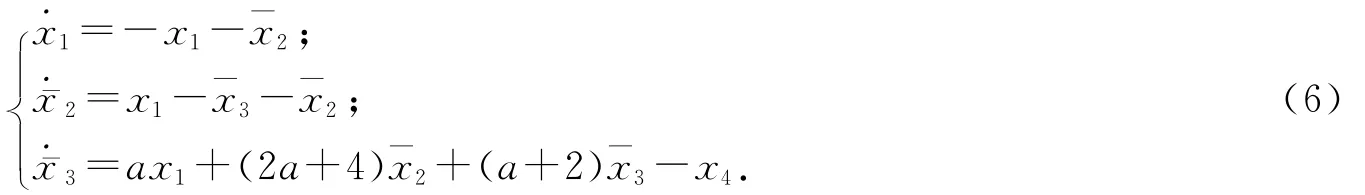
選取

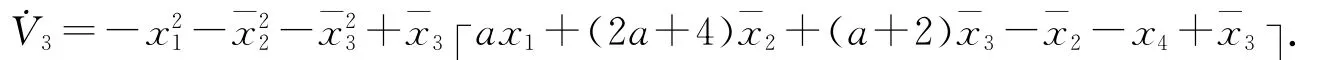
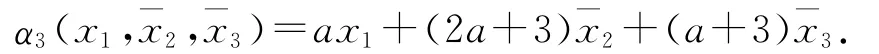
定義誤差變量

得到（x1，ˉx2，ˉx3，ˉx4）的子系統為：

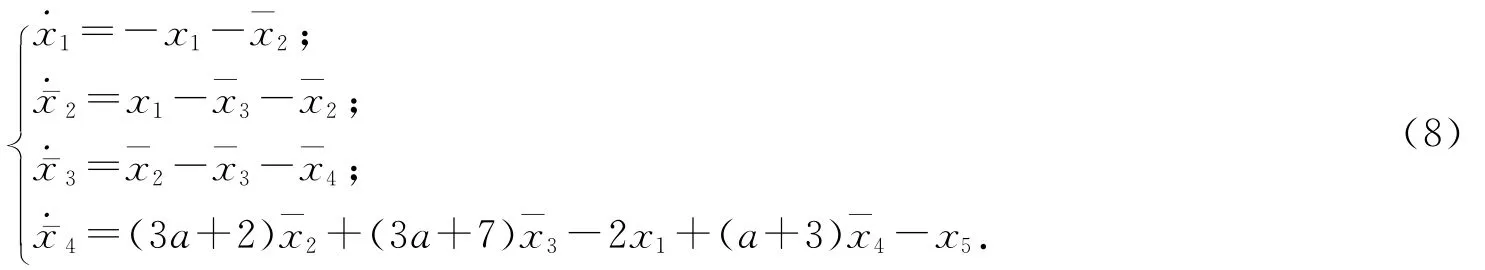
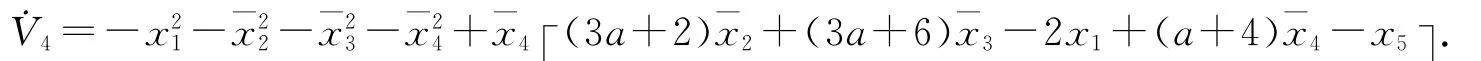
選取

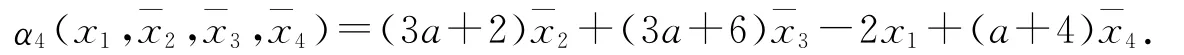
定義誤差變量

得到（x1，ˉx2，ˉx3，ˉx4，ˉx5）的子系統為：

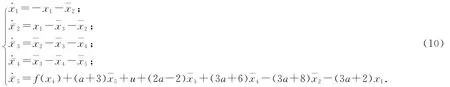
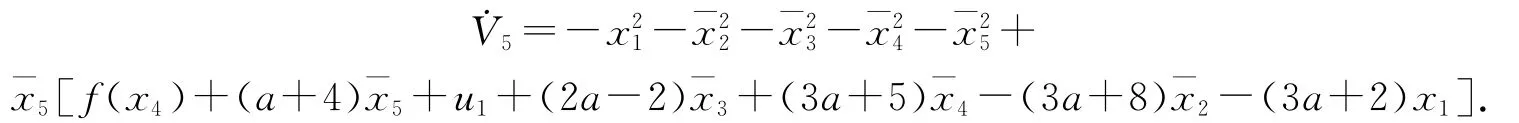
為使˙V5小于零，選取控制輸入

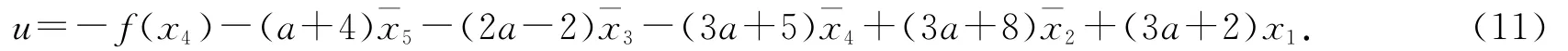
系統（10）在原點（0，0，0，0，0）得到穩定，當t→∞時，（x1，x2，x3，x4，x5）→（0，0，0，0，0）.

取超混沌Rossler系統（2）中的參數a＝0.3，b＝4，c＝1，d＝2，變量的初始值為x1（0）＝1，x2（0）＝1，x3（0）＝－1，x4（0）＝1，x5（0）＝－1，采用的時間步長為0.001，圖2為加入控制器u后，超混沌Rossler系統能夠被控制到原點（0，0，0，0，0）.

3 超混沌Rossler系統同步

設系統（1）為驅動系統，響應系統為：

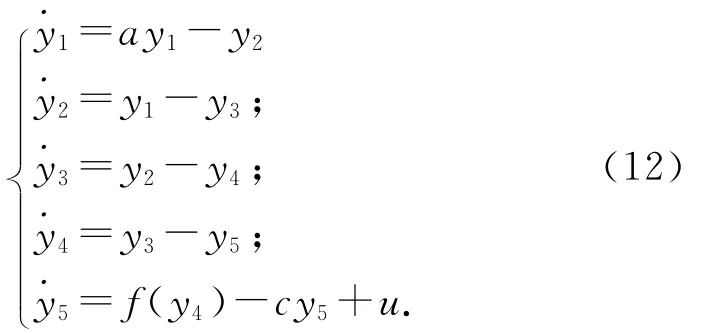
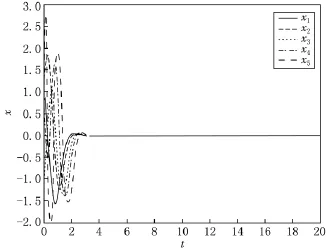
圖2 Backstepping方法實現超混沌Rossler系統控制結果

其中f（x4）＝2b（x4－d）H（x4－d），H（x4－d）是單位階躍函數，同樣響應系統中的

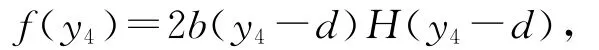
其中u是需要設計的控制器.令誤差變量為e1＝y1－x1，e2＝y2－x2，e3＝y3－x3，e4＝y4－x4和e5＝y5－x5，對超混沌Rossler系統（12）控制器的設計如下：

定義z1＝e1＝y1－x1，則˙z1＝ae1－e2，設z2＝e2－α1，其中α1是一個待設計的虛擬控制器.

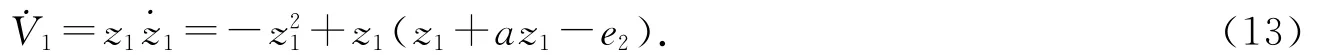
選取虛擬函數α1（z1）＝（a＋1）z1，則˙V1＝－z21－z1z2，˙z1＝－z1－z2.

定義

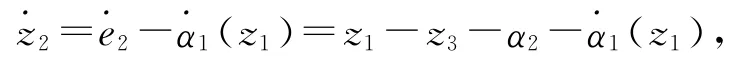
其中α2是虛擬函數，設z3＝e3－α2，選取Lyapunov函數，則

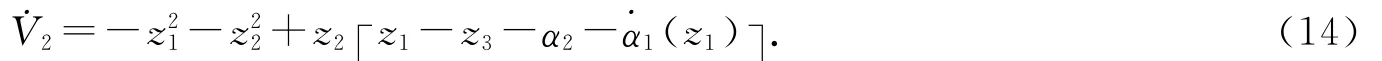
選取虛擬函數α2（z1，z2）＝（a＋1）z1＋（a＋2）z2，則˙V2＝－z21－z22－z3z2，˙z2＝z1－z3－z2.

定義

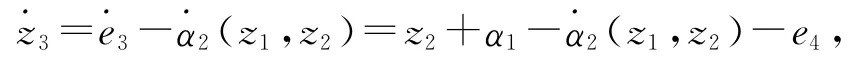
設z4＝e4－α3，選取Lyapunov函數，則

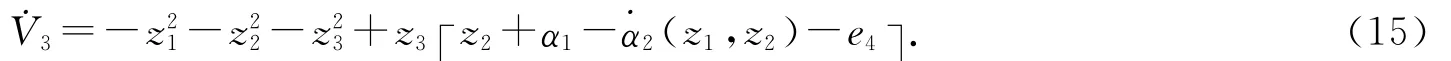
選取虛擬函數α3（z1，z2，z3）＝az1＋（2a＋3）z2＋（a＋3）z3，則

定義

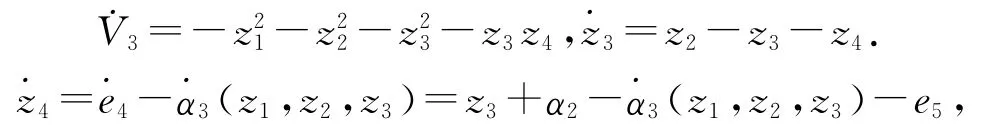
設z5＝e5－α4，選取Lyapunov函數，則

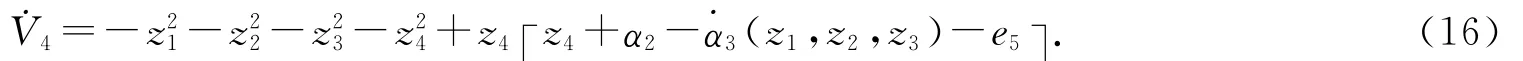
選取α4（z1，z2，z3，z4）＝（3a＋2）z2＋（3a＋6）z3－2z1＋（a＋4）z4，則

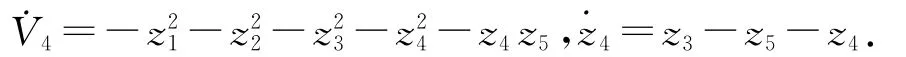
定義

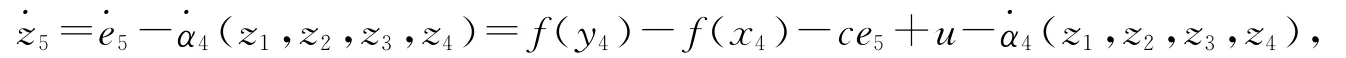
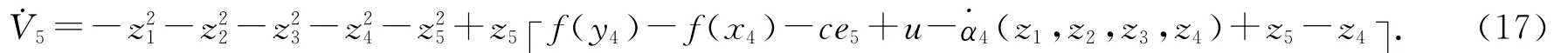
得到控制輸入u為

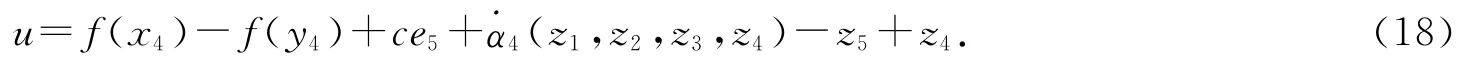
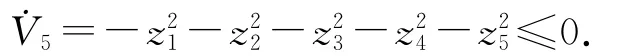
由以上推導可知，當取控制器u時，這就說明在基于Backstepping方法實現超混沌Rossler系統設計的控制器作用下，實現了驅動系統與響應系統的同步.采用四階Runge－Kutta法求解方程（1）和（12），選取時間步長為0.01s，驅動系統（1）的初始值選取為x1（0）＝1，x2（0）＝2，x3（0）＝3，x4（0）＝4，x5（0）＝5，響應系統（12）的初始值選取為y1（0）＝1，y2（0）＝1，y3（0）＝1，y4（0）＝1，y5（0）＝1，得到同步誤差曲線如圖3所示.

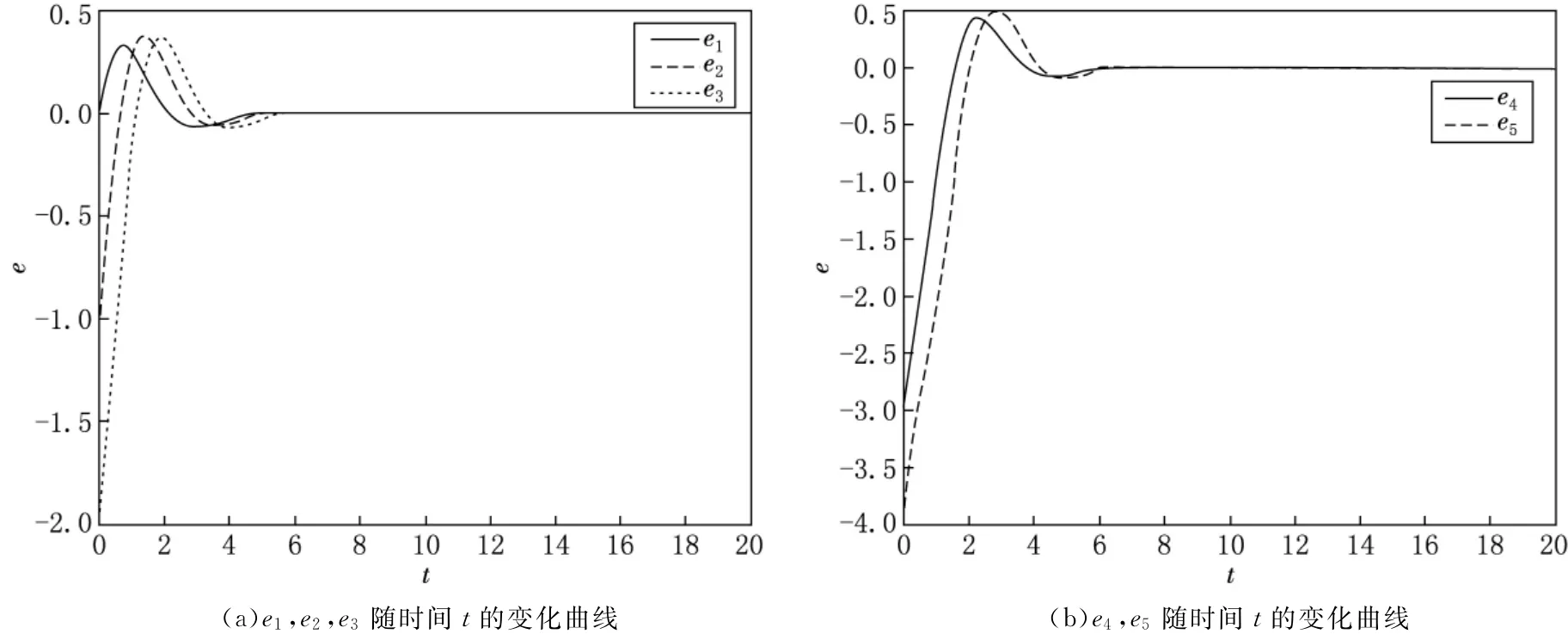
圖3 Backstepping方法實現超混沌Rossler系統同步的誤差曲線

由圖3的數值計算結果可以看出，在很短的時間內，誤差e1（t），e2（t），e3（t），e4（t），e5（t）已分別精確地穩定在零點，即驅動系統（1）與響應系統（12）達到了同步.

4 結論

對超混沌Rossler系統，本文利用Backstepping方法，只需要一個控制器實現了超混沌Rossler系統控制到零點，同時也只使用一個控制器，較好地實現了初值不同的2個超混沌Rossler系統同步，數值仿真結果表明了這種控制方法的有效性.

［1］ OTT E，GREBOGI C，YORKE J A.Controlling chaos［J］.Phys Rev Lett，1990，64：1196.

［2］ CHEN G，DONG X.On feedback control of chaotic nonlinear dynamic system［J］.Bifurcation and Chaos，1992，2：407－411.

［3］ CHEN S，LüJ.Parameters identification and synchronization of chaotic systems based upon adaptive control［J］.Phys Lett A，2002，19（4）：299－353.

［4］ LIAO T L，LIN S H.Adaptive control and synchronization of Lorenz systems［J］.J Franklin Inst，1999，336：925.

［5］ YASSEN M T.Chaos control of Chen chaotic dynamical system［J］.Chaos，Solitons ＆Fractals，2003，15：271.

［6］ WU Z M，XIE J Y，FANG Y Y.Controlling chaos with periodic parametric perturbations in Lorenz system［J］.Chaos，Solitons and Fractals，2007，32：104－112.

［7］ YASSEN M T.Chaos control of Chen chaotic dynamical system［J］.Chaos，Solitons and Fractals，2003，15：271－283.

［8］ YU Y G，ZHANG S C.Controlling uncertain Lüsystem using Backstepping design［J］.Chaos，Solitons and Fractals，2003，15：897－902.

［9］ TAN X H，ZHANG J Y，YANG Y R.Synchronizing chaotic system using Backstepping design［J］.Chaos，Solitons and Fractals，2003，16：37－45.

［10］ YASSEN M T.Controlling，synchronization and tracking chaotic Liu system using active Backstepping design［J］.Phys Lett A，2006，8（67）：1－6.

［11］ YASSEN M T.Chaos control of chaotic dynamical systems using Backstepping design［J］.Chaos，Solitons and Fractals，2006，27：537－548.

［12］ 岳麗娟，陳艷艷，彭建華.用系統變量比例脈沖方法控制超混沌的電路實驗研究［J］.物理學報，2001，50（11）：2097－2102.

Controlling and synchronizing hyperchaotic Rossler system using Backstepping design

WANG Shi1，YANG Ji2，LUAN Hong－xia3
（1.Office of Information Management and Planning，Northeast Normal University，Changchun 130024，China；2.Department of Basic Course，Aviation University of Airforce，Changchun 130022，China；3.School of Physics，Northeast Normal University，Changchun 130024，China）

This paper presents a Backstepping design method for controlling and synchronizing hyperchaotic Rossler system.In each recursive procedure，the virtual controller is designed for the differential of Lyapunov function negative definite.The controller is designed when the error system is stabilize by the stability theory of Lyapunov.The only one controller is needed for controlling and synchronizing hyperchaotic Rossler system using Backstepping design.The simulation results verify the effectiveness of involved controllers.

control；synchronize；Backstepping method；hyperchaotic Rossler system

O 415 ［學科代碼］ 120·20

A

（責任編輯：石紹慶）

1000－1832（2014）02－0069－05

10.11672／dbsdzk2014－02－014

2014－01－24

國家自然科學基金資助項目（10847110）；吉林省自然科學基金資助項目（201115008）.

王石（1979—），男，碩士，工程師，主要從事信息安全研究.