力-位移分控多點成形鞍面回彈的數值模擬研究

李 穎，王衛衛，賈彬彬，于靜泊

（哈爾濱工業大學（威海），山東 威海264209）

0 引言

多點成形是由一系列規則排列、高度可調的基本體形成離散曲面代替傳統模具進行三維曲面成形的板材柔性加工技術[1]。由于基本體與板材接觸面積的大幅度減少，常導致曲面成形時板材厚向約束不足，容易產生成形缺陷，如壓痕、起皺、回彈等[2]。利用力-位移分控的多點成形方法，可以很好地克服成形失穩、起皺等缺陷。但回彈現象是影響其成形質量的一個重要因素。

因此，在力-位移分控的多點成形中，研究回彈的影響因素對成形過程的控制和成形質量的提高具有重要的指導意義。文獻[3-5]分別對不同參數的球面、圓柱面和帆面進行了力-位移分控的多點成形數值模擬，并利用經典回彈理論分析了其回彈的影響因素。本文則利用力-位移分控的多點成形方法，對不同參數的馬鞍面進行數值模擬，并研究了回彈對板材成形性能的影響。

1 力-位移分控多點成形簡介

力-位移分控的多點成形方法是通過分別控制板材兩側點狀模具群的作用力或位移量來進行成形，能保證在整個成形過程中，板材始終處于上下點狀模具群的夾持約束中，實現曲面板材的有約束成形。其工作原理如圖1 所示。上下基本體的行程是由上基本體的螺桿長度控制的，而成形過程中板材受到的成形作用力是由下基本體的液壓缸控制的。從而使成形過程中的基本體的位移和成形作用力分別由上下基本體控制。

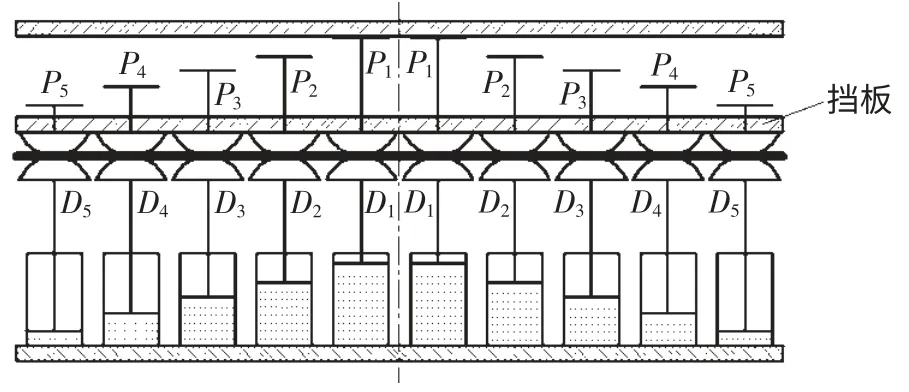
圖1 力-位移分控多點成形工作原理圖

2 有限元模擬

2.1 曲面造型

一半徑為R，圓心在（0，0，a）的圓（圖2a），使其繞y 軸旋轉一周，可以得到一個圓環曲面，其方程為當a≠0 時，圓環的內半環部分（圖2b）相當于一個鞍面，鞍面方程可寫為[6]

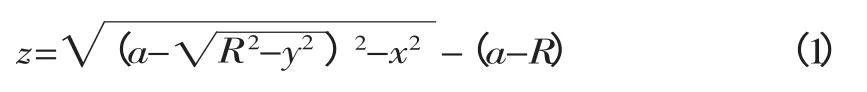
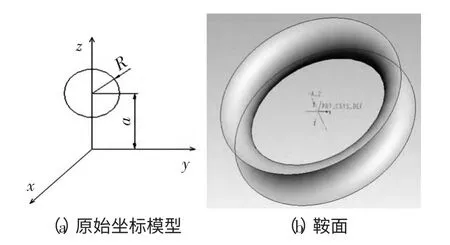
圖2 鞍面示意圖

2.2 基本算法的選擇

ANSYS/LS-DYNA 將LS-DYNA 和ANSYS 程序強大的前后處理結合起來。LS-DYNA 的顯式算法能快速求解瞬時大變形力學、大變形和多重非線性準靜態問題以及復雜的接觸碰撞問題。針對力-位移分控多點成形的特點，加載沖壓過程采用顯式算法，回彈過程采用隱式算法，不但計算精度高，并且計算時間短。

2.2.1 加載過程采用顯式算法

在動力學問題中，如果采用顯式算法進行分析時，可建立虛功方程為

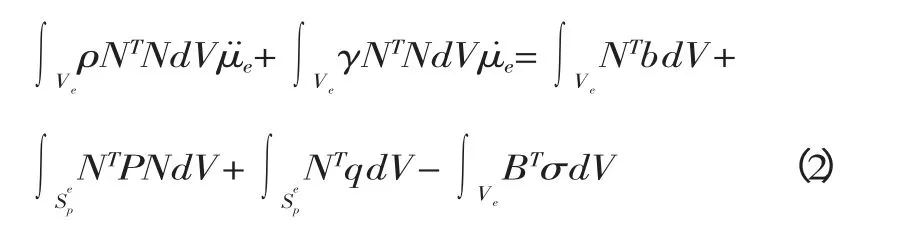
式中：ρ——質量密度；

γ——阻尼系數；

S——表面積，S=Sp+Sc+Su；

p——Sp上給定表面力；

b——單位質量上作用體積力；

q——Sc另一物體接觸的接觸表面力；

V——體積。

將式（2）應用于離散后的所有單元，并將所有的單元方程集合構成整體有限元方程

式中：M——質量矩陣；

C——阻尼矩陣；

U¨——節點加速度；

U˙——節點速度向量；

P——節點外力矢量；

F——節點內力矢量。

2.2.2 卸載過程采用隱式算法

彈塑性變形體內任一單元的虛功方程的矩陣形式為

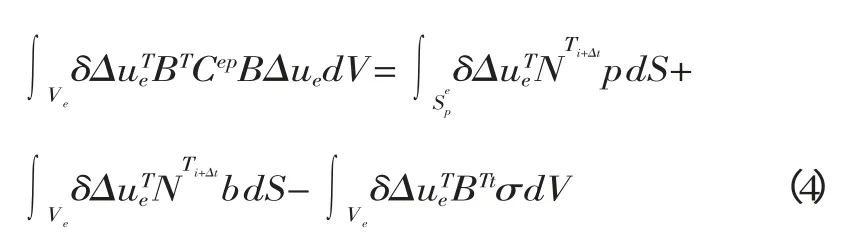
式中：Cep——增量彈塑性矩陣。

由式（2）得到整個變形體有限元方程

式中：Kt——t 時刻的剛度矩陣；

Ut+1——t+1 時刻位移增量；

Pt——t 時刻整體節點外力向量；

Ft——t 時刻整體節點內力向量。

2.3 有限元模型基本設置

力-位移分控的多點成形數值模擬在顯式的沖壓成形階段采用的是BWC 殼單元，而在隱式回彈階段采用的是SHELL181 單元。成形的板材采用的是Q235 鋼板，故采用滿足Hill 厚向異性屈服準則的彈塑性非線性材料模型[7]。板料和模具的接觸采用SURFACE_TO_SURFACE（STS），接觸力計算采用罰函數法。剛性面與下基本體之間的接觸定義為剛性面接觸RIGID BODY TO RIGID BODY（ROTR），通過定義力-變形曲線阻止下基本體的穿透。

本文采用上、下基本體群各為10×10，基本體間距20mm，基本體球頭直徑20mm，板料尺寸200mm×200 mm，板料厚度分別1mm、1.5mm、2mm、2.5 mm、3mm。有限元模型如圖3 所示。

圖3 有限元模型

3 回彈的表示及計算

3.1 回彈的表示方法

板料的彎曲成形總是伴有彈性變形的，所以卸載后，總變形中的彈性變形部分立即恢復，引起板料的回彈，其結果表現在彎曲件曲率和角度的變化。

目前，回彈的表示方法有很多，主要有經典沖壓理論的回彈表示法、回彈比及回彈角等。為了直觀反映回彈的大小，本文采用回彈角來表示成形前后的回彈量：

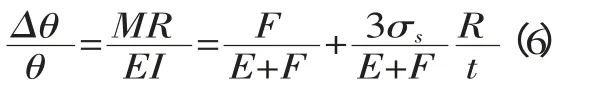
σs——材料屈服應力，Pa；

R——板材目標彎曲半徑，m；

t——板材的厚度，m；

E——彈性模量，Pa；

F——硬化模量，Pa。

也可用下式表示：

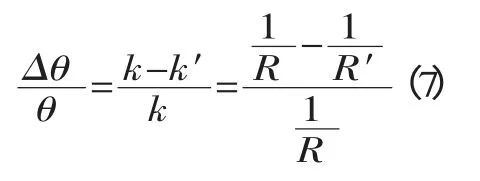
式中：k——板材回彈前的平均曲率；

k′——板材回彈后的平均曲率；

R——板材回彈前的平均曲率半徑；

R′——板材回彈后的平均曲率半徑。

3.2 回彈的相關計算

以板材回彈后的平均曲率半徑k′為例進行計算。

在數值模擬的建模過程中，為簡化模型，取四分之一模型，則模型的尺寸為100mm×100mm，網格劃分為2.5mm，這樣模型每條邊上的節點數為41 個（分別編號為1～41）。考慮到直邊效應和邊緣起皺情況，進行回彈計算時，去除成形缺陷明顯的第一個節點和最后四個節點，共剩下36 個節點（即編號為2～37），平均分成兩組，第一組為編號為2～19 的節點，第二組為編號為20～37 的節點，任取第一組節點an以及與之間隔十八個點的an+18, 從ANSYS 中導出對應的坐標，如下所示：

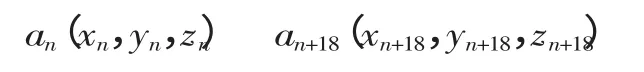
建模中選擇板料的中心點為坐標原點，若取y=0 方向為研究對象，成形結束后，各個節點x 坐標是一個定值，理想情況下z 也是定值，但是由于成形缺陷的存在，z 是隨節點變化的。因為是在xOz 平面內，所以y 是定值，為減少偏差，應對其計算18 次，取平均數后才求得其回彈后的平均曲率半徑R′：

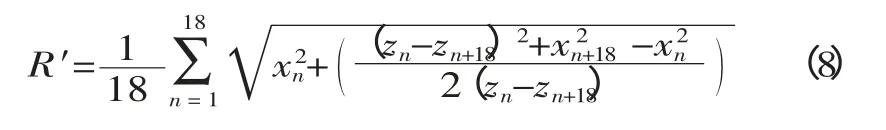
對板材回彈前的平均曲率半徑也可用上式求得。

4 回彈影響因素分析

回彈是板材整個成形過程中的積累效應，與材料特性、模具幾何形狀、摩擦接觸及成形力等很多因素有關，所以在板材成形中，回彈是非常復雜的問題。本文主要從成形板材的曲率半徑以及板材厚度這兩個方面來討論對回彈的影響。

4.1 成形曲率半徑對回彈量的影響

對于鞍面的形狀參數a 和R，它們分別決定了y=0 和x=0 這兩個方向的曲率半徑。其中，x=0（即y軸）的理論曲率半徑為R，而y=0（即x 軸）的理論曲率半徑為a-R。本文先對y=0 方向的回彈進行分析，令x=0 方向的曲率半徑不變分別設為240mm、280mm 和320mm，改變y=0 方向的曲率半徑即為變化a 值，具體參數為a480、a720 以及a960，成形力均為1000N，對其進行作圖分析，如圖4a、b、c 所示。

由圖可見，在成形力為1000N，且板厚及曲率半徑R 相同時，隨著a 值的增大即y=0 方向曲率半徑的增加，其回彈量呈現增長的趨勢。分析原因：理論上說，回彈量的大小與成形后板料內部應力有著直接的關系，材料內部應力的大小又由板料變形量決定，曲率半徑的大小決定了變形量的大小。當曲率半徑較小時，材料的變形量大，成形結束后塑性變形占總變形的比例也越大。與之相反，當曲率半徑較大時，板材外表面的縱切向變形程度減小，其中塑性變形和彈性變形成分相應都減小，但在總變形中彈性變形比例比較大，因此回彈也比較大，卸載后彈性變形消除，因而回彈量增大[8]。模擬結果進一步論證了該結論。

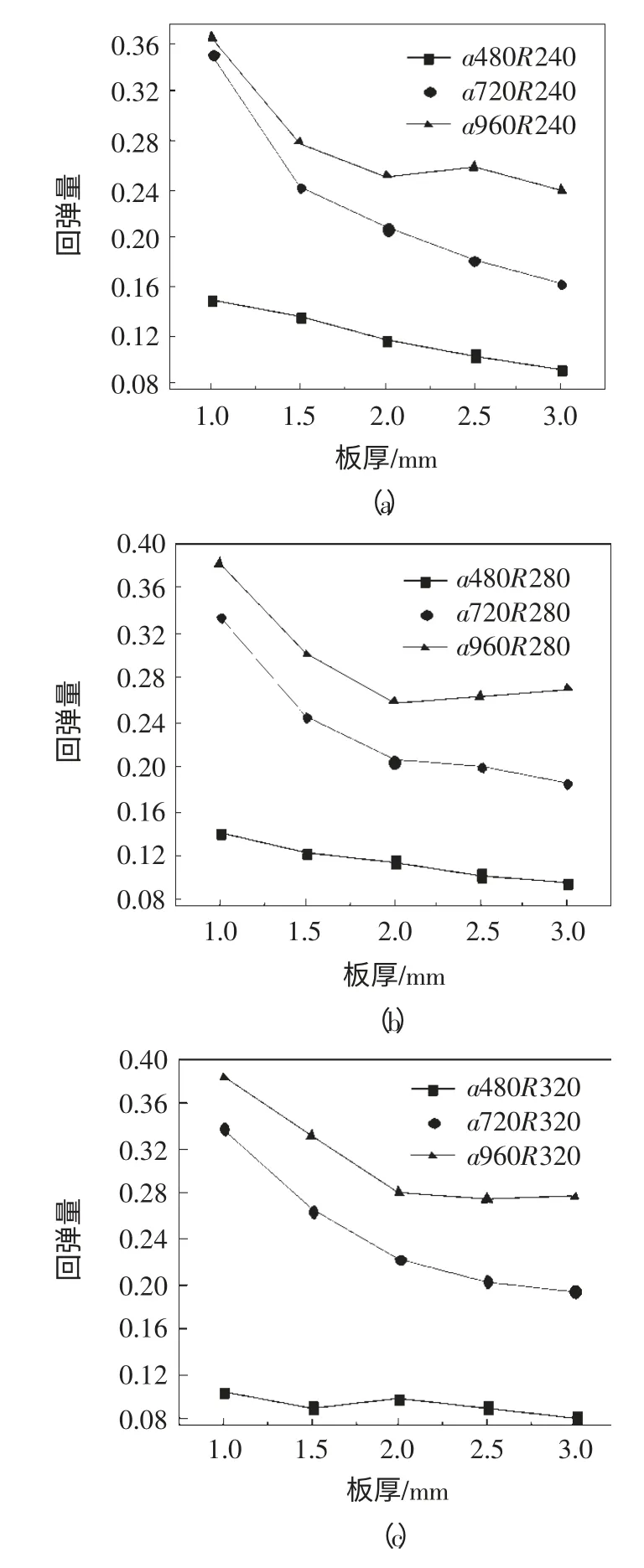
圖4 回彈量隨曲率半徑變化情況（y=0）

x=0 方向曲率半徑對其回彈的影響則如圖5a、b、c 所示。由圖可見，在成形力為1000N 時，x=0 方向均發生了負回彈，可見，x=0 方向的回彈是受到了y=0 方向回彈的影響。圖5a 中，當a=480 時，隨著R值的增大即x=0 方向曲率半徑的增加，其回彈量呈現減小的趨勢。究其原因：一方面，隨著R 值的增大，x=0 方向所產生的正回彈量有所增加，更多地抵消了負回彈；另一方面，隨著R 值的增大，即a-R 減小，則y=0 方向所產生的回彈減小，對x=0 方向的負回彈影響也相應減小。圖5b、c 中，當a 為720 及960 時，隨著R 值的增大即x=0 方向曲率半徑的增加，其回彈則呈現出與a=480 相反的趨勢，即負回彈增大。分析原因：

4.2 板厚對回彈量的影響

為了研究板厚對回彈量的影響，本文選取了鞍面參數為a720，在成形力為1000N 下，對應于5 個板厚（1mm、1.5mm、2mm、2.5mm、3mm）的數值模擬結果，并以y=0 和x=0（針對1/4 模型而言）的兩條邊作為研究對象，如圖6、7 所示。

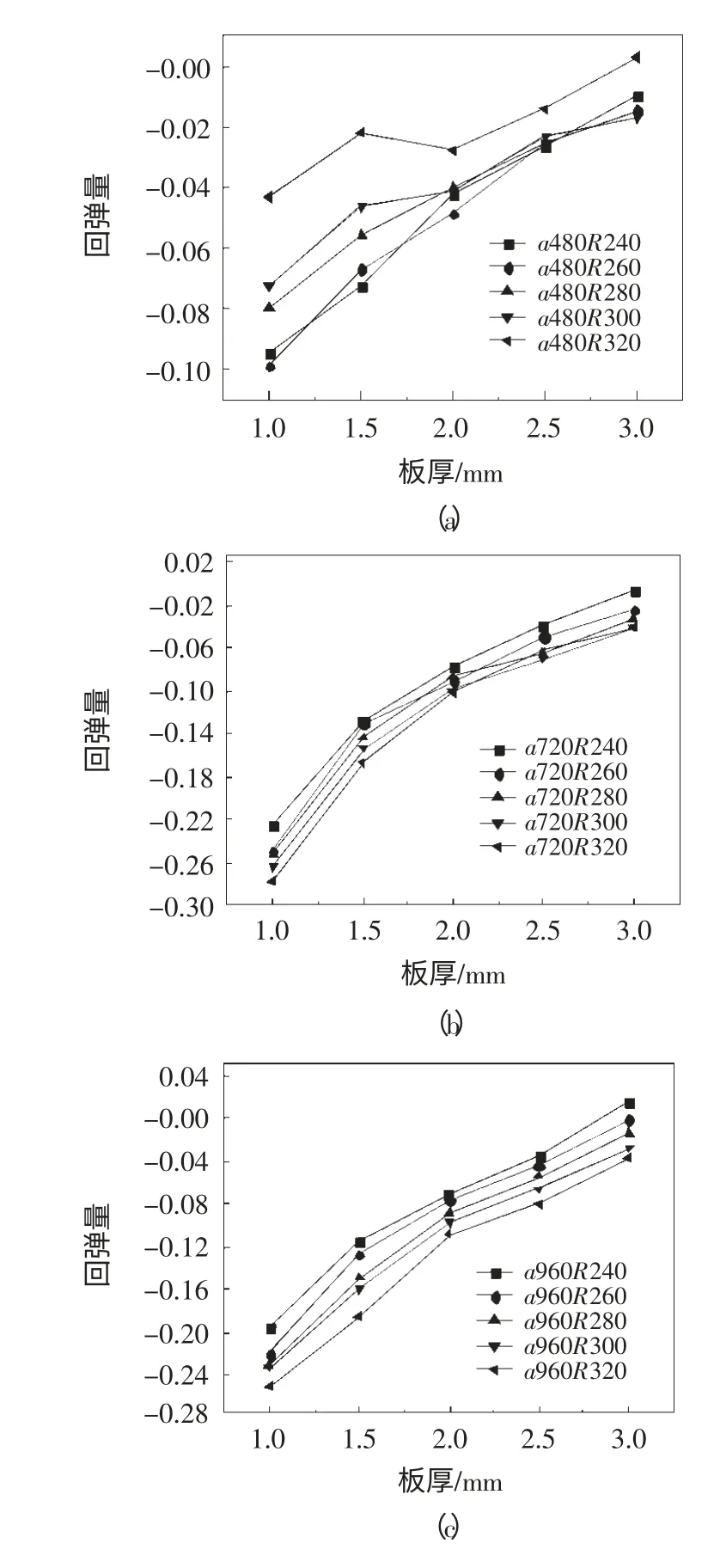
圖5 回彈量隨曲率半徑變化情況（x=0）

由圖顯然可見，在成形力1000N 下，無論是x=0方向還是y=0 方向，隨著板厚的增加，其回彈量都在減小。由于板厚越厚，板材的變形抗力越大，成形時所需要加載的彎矩也越大，因此卸載后的回彈量則越小[9]。同樣的，鞍面在x=0 方向收到了y=0 方向回彈的影響而產生了負回彈。從圖10、11 可以分析出，隨著板厚的增加，x=0 方向上的回彈受到y=0 方向回彈的影響越小。也就是說，板厚越小，則y=0 方向對x=0 方向回彈的影響越顯著。

5 結論

（1）雙曲率馬鞍面在發生回彈時，隨著曲率半徑的增大，則該方向的回彈也在增大。

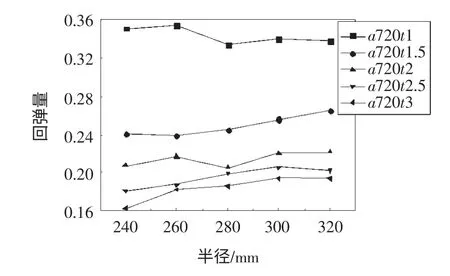
圖6 回彈量隨板厚變化情況（y=0）

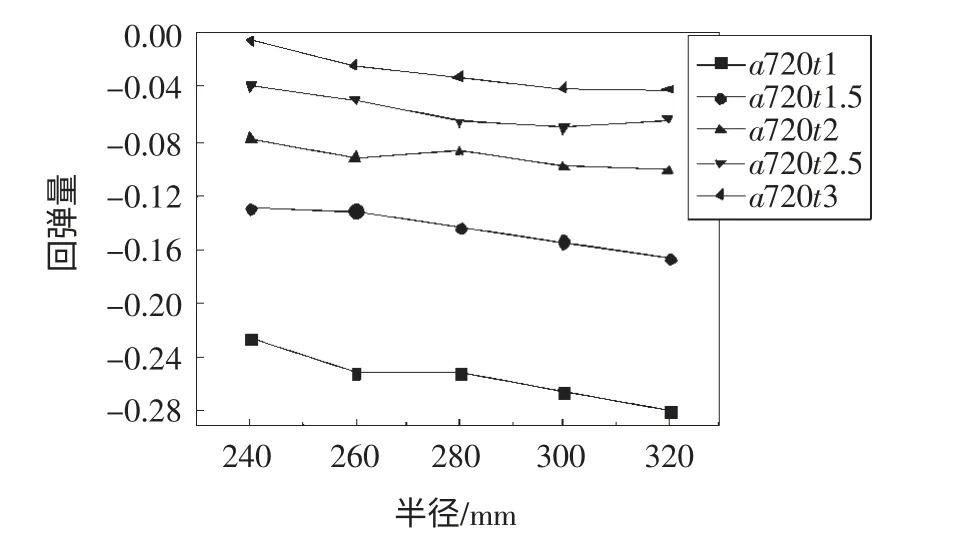
圖7 回彈量隨板厚變化情況（x=0）

（2）雙曲率馬鞍面在發生回彈時，隨著板厚的增大，則兩個方向的回彈均在減小。且起主導作用的方向對另一方向的回彈影響會隨著板厚的減小而越顯著。

[1]Li M Z.Cai Z Y,Sui Z,etc.Multi-point forming technology for sheetmetal[J].Journal of Materials Proceessing Technology,2002,129（1-3）:333-338.

[2]李明哲，中村敬一.多點成形中缺陷的發生及控制[C]//日本第43回塑性加工聯合講演會論文集.京都，1992.

[3]于靜泊，王衛衛，賈彬彬.力-位移分控多點成形球面回彈的數值模擬[J].煤礦機械，2009，03（3）：61-63.

[4]崔愛愛，王衛衛，陳 澤，等.圓柱面力-位移分控多點成形的數值模擬研究[J].鍛壓裝備與制造技術，2011，46（5）：91-95.

[5]Wang Weiwei,Chen Ze,etc（2012）Numerical simulation on the multi-point forming of sail surfaces under force-displacement separated control.Applied Mechanics and Materials,217-219,1959.

[6]高東強，胡 林.基于ISDX 的雙曲拋物面造型[J].制造業信息化，2005，11：112-113.

[7]Hill R.A Theory of the Yielding and Plastic Flow of Anisotropic Metals.Roy.Soc.，London Proc.，1948.

[8]楊建鳴，郝 潔，郭曉妮.基于ANSYS/LS—DYNA 的板材多點成形中回彈的數值模擬[J].裝備制造技術，2011，（2）：1-3.

[9]麻桂艷，付文智，李明哲.中厚板多點成形中回彈的數值模擬[J].鍛壓技術，2006，（4）：141-144.