仿真機房系統的優化設計

劉仁云，朱少東，王恩娜，羅雷鳴，李亞瑞

(長春師范大學數學學院，吉林長春 130032)

仿真機房系統的優化設計

劉仁云，朱少東，王恩娜，羅雷鳴，李亞瑞

(長春師范大學數學學院，吉林長春 130032)

本文選擇具有普適性的機房作為研究對象，首先對機房內的溫度、位置、風速等參數進行搜集和處理，建立了基于插值擬合方法的機房熱分布數學模型，得到了服務器最優任務分配方案，并根據方案對出風槽的風速和溫度等參數進行調節，以達到降低機房內的溫度極值點的目的，最后實現了機房散熱系統的優化設計。

建立模型；樣條插值；熱分布；最優任務

對于多任務、高性能計算處理的數據中心或互聯網中心(DC、IDC)的基礎設施經常依據經驗來部署安排，這樣的方法具有隨意性和非科學性，經常導致機房溫度過高、機房設備不能健康運行等問題，使得數據中心將大量資金用于系統冷卻的設備上。因此，有必要對數據中心的散熱系統進行仿真優化設計，以達到節能目的，實現最佳能源利用效率。本文以常見的計算機機房系統為例進行仿真優化設計。

1 問題分析、數據收集與處理

機房的溫度分布主要受到服務器所產生的熱量及其擺放位置的影響，服務器產生的熱量又由其承擔的工作量(或任務)決定。因此，首先要了解機房內溫度的分布情況；其次尋找最優任務分配方案；最后根據分配方案調節儀器設備的位置和影響溫度的相應參數。具體步驟如下：(1)對機房內的溫度和風速的數據進行采集和處理；(2)繪制冷、熱通道的流場分布圖和熱分布圖，求出溫度極值點；(3)建立熱分布模型，確定不同任務量下的最優任務分配方案；(4)根據分配方案調節出風槽的溫度與風速等參數以滿足設計規范要求，從而實現仿真機房的優化設計。

1.1 測量數據

根據機房內部設施的尺寸數據做出機房的示意圖(圖1)，采集溫度、風速、位置等數據，并對數據進行分析處理。

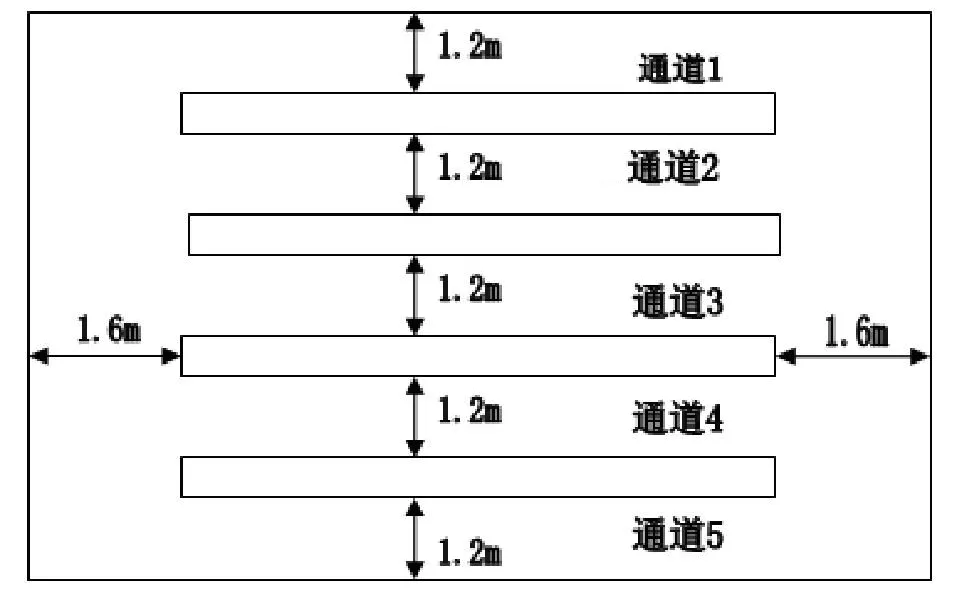
圖1 機房示意圖

其中，X為通道位置，m；Y為機柜距離空調的位置，m；Z為機柜距地板的高度，m；T為機房溫度，℃；Ri為任務量，0≤Ri≤1，i=1,2,3,4；V：風速，m·s-1。

1.2 計算溫度最高位置

對實驗數據進行樣條插值計算，并運用數學軟件Matlab繪制冷、熱通道的熱分布即T(Y,Z)及流場分布圖。

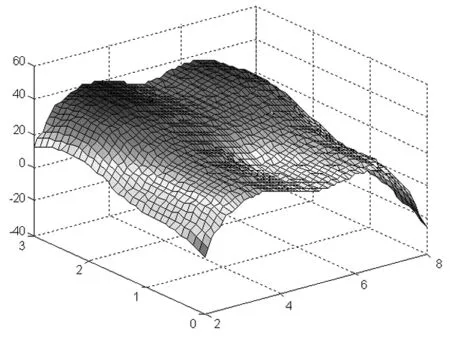
圖2 冷通道的熱分布圖

圖3 熱通道的熱分布圖

圖4 冷通道的流場分布圖

圖5 熱通道的流場分布圖

從圖2至圖5可見，最高溫度發生在熱通道內。利用Matlab可求出曲面的極值點為T(6.8,2.1)=56.043，即溫度最高點為熱通道在距空調6.8m、距地板2.1m處，最高溫度為56.0436℃。

2 模型建立

設每個機柜(服務器)任務量相同，利用Matlab研究溫度T與機柜擺放位置X、Y、Z之間的關系。根據4個機柜任務量R的不同，繪制R=0.2、R=0.3、R=0.5時，溫度T與機柜距空調位置Y的關系曲線圖(圖6)，溫度T與機柜距地板高度Z的關系圖(圖7)。

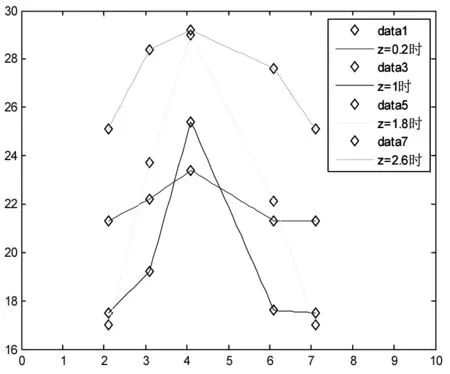
圖6 溫度與機柜距空調位置的關系圖

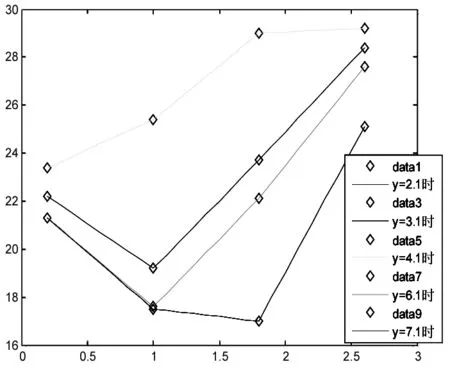
圖7 溫度與機柜距地板高度的關系圖

根據所收集的數據，擬合相同任務量R下，機柜距空調位置Y、機柜距地板高度Z與溫度T的函數關系，經過程序調試，得到熱分布的數學模型為

T=m+nY+pZ+qY2+kZ2.

(1)

設模型誤差小于等于0.01時模型符合要求精度，其各項參數為

m=19.5004-6.155X-23.8023R+0.6569X2+22.8186R2，

n=2.0474+2.0937X+18.8778R-0.2250X2+17.6572R2，

p=-3.6337+1.0113X-9.358R-0.1118X2-7.7347R2,

q=-0.233-0.228X-2.0545R+0.0246X2+1.9136R2,

k=1.2342-0.2427X+3.3913R+0.0272X2-2.7986R2.

從任務量相同的測量中驗證熱分布模型(1)，得其絕對誤差為η=0.005≤0.01，說明該數學模型建立符合要求。

3 服務器的最優任務分配方案

在Matlab中繪制任務量R1=0.2，R2=0.3，R3=0.5時不同高度4個機柜的溫度關于X，Y，Z的分布圖T(X,Y,Z) (由于篇幅問題，只給出R1=0.2時的分布圖)。

圖8 h=0.2的溫度分布圖

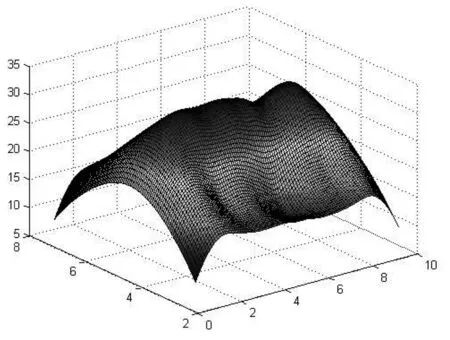
圖9 溫度與機柜距地板的高度的關系圖

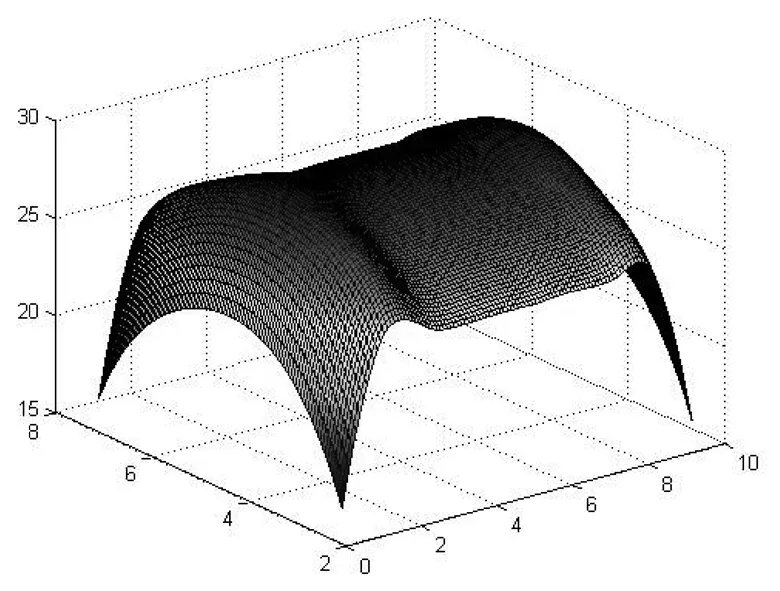
圖10 h=1.3的溫度分布圖

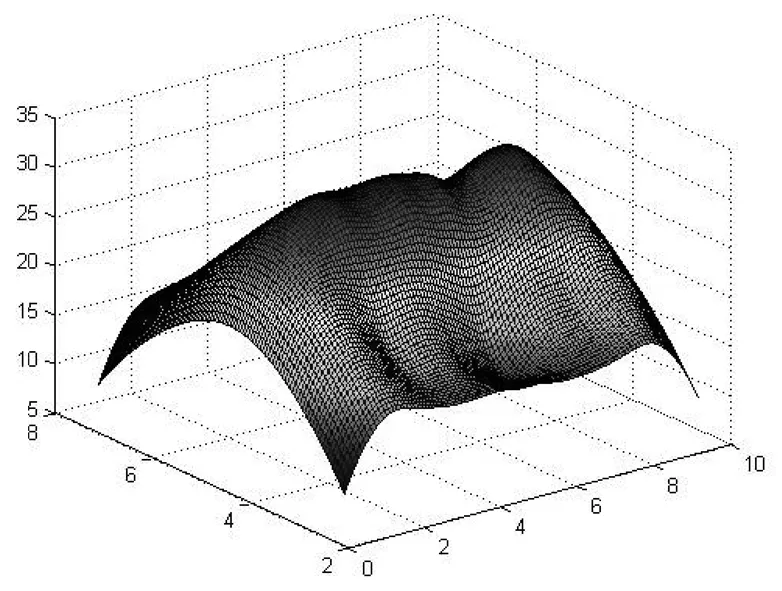
圖11 h=2.6的溫度分布圖

用imregionalmax 函數找出R1=0.2，R2=0.3,R3=0.5時的溫度極值分別為T(2.4162,4.1261,1.7758)，T(4.0889,4.1261,1.7758)，T(7.2485,4.1222,1.7758)。

由于我們測量的數據中沒有極值點這3個數據，所以通過點A1(2.4,4.1,1.8)，A2(4.1,4.1,1.8)，A3(7.2，4.1,1.8)進行模擬，結合上述熱分布模型得不同任務量下極值點處溫度分布表(表1)。

表1 溫度極值點分布表

結合表1可知，當機柜一任務量增加到0.8時，只有點A溫度發生較大的變化；機柜二任務量增加到0.8時，只有點B溫度發生較大的變化；機柜四任務量增大到0.8時，只有點C發生較大的變化；機柜三任務量增加時3個點的溫度幾乎都沒有變化。由此推斷點A、B、C三點的最高溫度只與機柜一、二、四相關。根據A、B、C三點的位置數據，利用指數函數擬合得到與位置相關的最優任務分配模型：

T1=26.7333×1.4483R1,T2=26.0368×1.5055R2,T3=26.4856×1.4760R3.

(2)

其中，Ri為第i個機柜的任務量，Ti為由第i個機柜得出的溫度的極值點。

根據模型分配任務量，求出在此方案下的機房最高溫度(表2)。

表2 任務量分配表及機房溫度狀態

根據《電子信息系統機房設計規范》C級要求，機房溫度應控制在35℃之下，仿真模擬所得的最高溫度符合要求，即服務器所分配的任務量為最優分配。

4 出風槽風速及溫度參數調節

機房內溫度的調節是通過出風槽的溫度及風速來實現的。冷氣由出風槽通過冷通道向機房內輸入，從機柜邊緣進入熱通道，從而達到降低機房內熱點溫度的目的。而風速V與Y、Z、T的關系可由公式(3)確定。

V=0.5654+0.0867Z+0.045Y+0.0044T0+0.03V0.

(3)

其中，V0為出風槽的風速(m·s-1)，T0為出風槽的溫度(℃)。

應用多元線性函數回歸建立機房內某點的溫度與該點距空調距離、距地板高度、風速的函數關系。

T=11.0669+3.8224Z+0.8356Y+8.2268V.

(4)

V=(T-11.0669-3.8224Z-0.8356Y)/8.2268.

(5)

根據《電子信息系統機房設計規范》C級要求，控制機房溫度在35℃以下。在機房中若熱點溫度T大于35℃，則將該點需要降至的合理溫度值及相應的Y、Z數據帶入函數式(5)，求出相應風速V，將V帶入函數式(3)，進而求出空調的送風速度。

5 模型檢驗

對不符合信息系統布置C級要求的熱點，進行相應的最優任務分配，計算出風口的送風風速及溫度，調節之后再對該熱點進行測量，會發現該熱點的溫度已經達到我們的要求，由此可確定此熱分布模型適用于普通機房的優化設計。

6 結語

本文根據機房的基礎設施狀態，對相應的實驗數據進行分析處理，建立了基于插值擬合的關于機房的熱分布數學模型，并給出了服務器的最佳任務分配方案，按照該方案對涉及機房溫度的儀器設備的參數進行調整。實現了機房熱分布仿真優化設計。經過實際應用的初步檢驗，該模型具有較好的實用性與合理性。

[1]Robinson D F,Hassan Hassan H A.Further Development of the (Enstrophy) Turbulence Closure Model[J].Journal of AIAA,1998(36):1825-1833.

[2]Pratap,V.S.,Spalding,D.B.Numerical Computions of the Flow in Curved Ducts[J].The Aeronautical Quarterly,1975,Aug.

[3]Eiseman,P.Retal.Development of a Three-Dimensional Turbulent Duct Flow Analysis[J].NASA CR3029,1978.

[4]董大校.基于MATLAB的多元非線性回歸模型[J].云南師范大學學報:自然科學版,2009(2):45-48.

[5]姜啟源,謝金星,葉俊.數學模型[M].3版.北京:高等教育出版社,2003.

[6]尹貞勤.程控交換機房空調設計探討[J].安徽建筑,1999(4):29-31.

[7]劉圣慶.解決數據中心散熱難點問題的方案探討[C].通信技術與標準,2008專刊.

[8]賈瓊,孫顙,郭永昊.模糊預測控制在VAV空調系統中的應用[J].建筑電氣,2008(6):42-44.

2014-04-12

劉仁云(1969- )，女，遼寧大連人，長春師范大學數學學院教授，博士，從事智能優化研究。

TP311.52

A

2095-7602(2014)04-0053-05