不同參照系里的功能關系
孫夢家
(景德鎮一中,江西 景德鎮 333000)
功能關系是中學物理乃至整個普通物理學中非常重要的關系。不論功還是能都和物體的運動有關,而物體的運動又和參照系的選取有關,那么功和能與參照系的選取有什么樣的關系?
1 問題提出
某人在以速度v行駛的大船上先后以速率u(相對于船)向船頭和船尾方向投出質量m的球。試問,在兩次投球中,他做的功是否相同?
解1:以地面為參照系,向船頭投球時,球的動能的增量為:

向船尾投球時,球的動能的增量為:
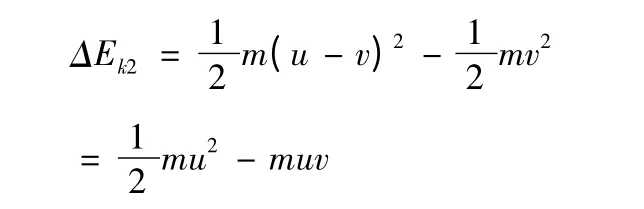
可見,兩次投球動能的增量不同,根據動能定理,兩次投球時人做的功也不同。
解2:以船為參照系,兩次投球中動能的增量為:

所以,兩次投球動能的增量相同,根據動能定理兩次投球人做的功也相同。這里,某人所做的功是將人消耗的生物能轉化為機械能。按生活常識可知,在兩次投球中,人所消耗的生物能應相同,而上面的兩種解法的結果卻不同,而計算似乎都合理,問題出在哪里呢?實質問題也就是,不同的參照系里的功能關系,即動能定理是否都成立,是否都一樣?
2 以地面為參照系研究
原題解法一的結果與實驗結果相違背,那么錯在哪里呢?問題出在當我們投球的時候,由于質點系(人、船、球組成)的動量守恒,輪船的速度也將發生改變,這變化導致輪船的動能改變,而船的動能改變也應該計算到投球時做的功中去。
在第一種情況下,球向前投,人、球與船組成的質點系的動量守恒即:
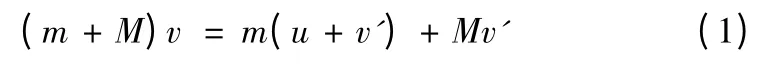
式中v'是球投出后船的速度,m是球的質量,M是人和船的質量:
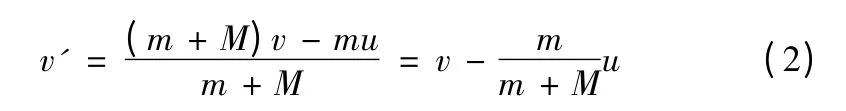
此時球的速度為:
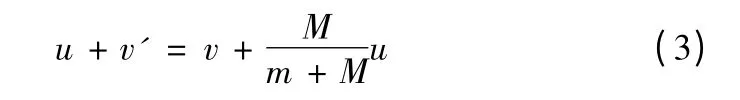
投球時做的功,應為人、球和船的動能之和,即:
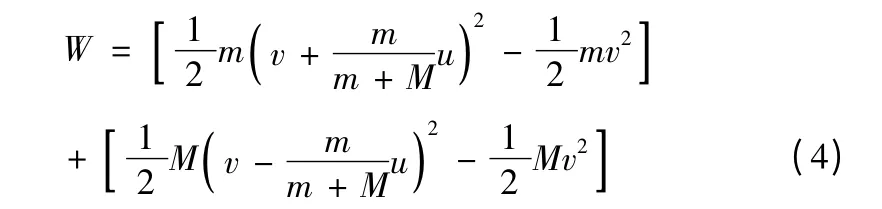
在(4)式中前一個方括號為球的動能增量,后一個括號中為人和船的動能增量。
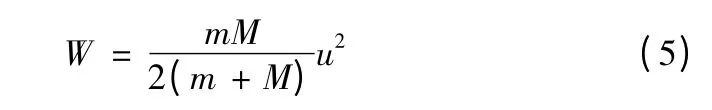
如果人和船的質量遠大于球的質量,即時,

在第二種情況下,球向后投時人做的功的計算與上面相似,將u改為-u即可,由(5)式可得:
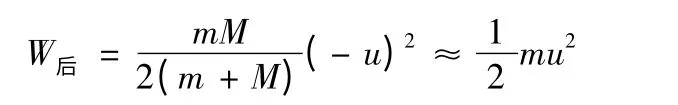
這結果與第一種情況相同。
通過以上的計算,使我們注意到:投球后,船的速度v'變化為(2)式所示,在M?m的前提下,只就速度而言,可以略去這一項,即可以認為船的速度不變,但就動能而言,因為要乘上M這一項,它引起人與船的動能變化是相當大的,故不能略去。
3 以輪船為參照系研究
我們注意到,上面的討論中以地面為參照系的情況下,雖然向前和向后投球人做的功相同,但計算結果與原題解法二給出的結果卻不相同,這又是為什么呢?從上面的分析中,我們看到投球后,輪船的速度要改變,從v變為v',這樣它相對地面就不再是勻速直線運動,也就是說,不再是一個慣性參照系,而在非慣性參照系中,要計入慣性力做功,動能定理才能成立。我們可以選取人、輪船與球的質心為參照系。因為質心以不變的速度v做勻速直線運動。如果船的質量M遠大于球的質量m,人、輪船與球的質心近似為人、船的質心。選質心參照系就是近似選人、輪船為參照系。所以以相對于船速度為u投球,不論是向前還是向后,所做的功都是近似成立條件是M?m,這樣結果就與上面以地面為參照系求出的結果一樣了。如果不滿足M?m的條件,就不能選人、輪船為參照系,而應嚴格地選地面或質心參照系來計算投球時做的功。
4 不同參照系中的功和能
4.1 動能定理
若以地面為參照系:設有一質點m,受力F作用,在力的方向上移動了一段距離S,v0是質點的初速度,v是質點的末速度。
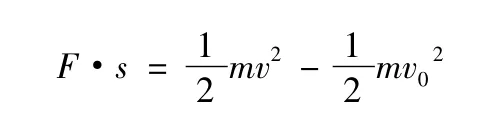
現在以另一個慣性參照系來觀察這個質點的運動,比如是在地面上以速度u勻速運動的汽車,以汽車為參照系。在汽車參照系中質點m的位移S',由伽利略變換S'=s-ut。質點的初末動能分別為
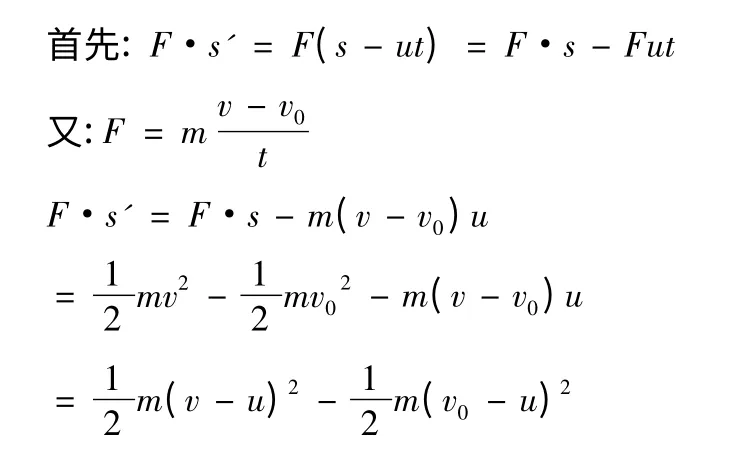
在質心系中:
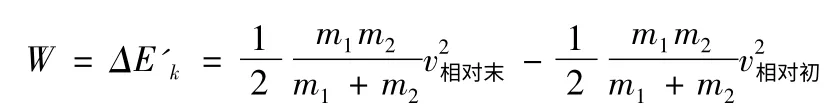
在質心系中人向前和向后投球時所做的功:
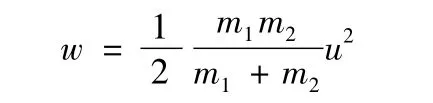
可見在不同慣性系中動能定理都是成立的。但是,在不同慣性系中動能的變化及力所做的功可以不同,因為在不同參照系的位移也可以不同。
4.2 質心參考系
根據柯尼希定理,質點系對慣性系的動能等于質點系對質心系的動能與質心對慣性系的動能之和。
設有m1,m2有組成的系統,m1,m2對地面參照系的速度分別為v1和v2,兩速度在同一直線上,則質心的速度:
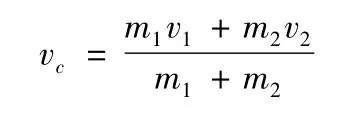
設E'k為質點系在質心系中的動能,Ek為質點系對慣性系的動能,Ekc為質心對慣性系的動能:
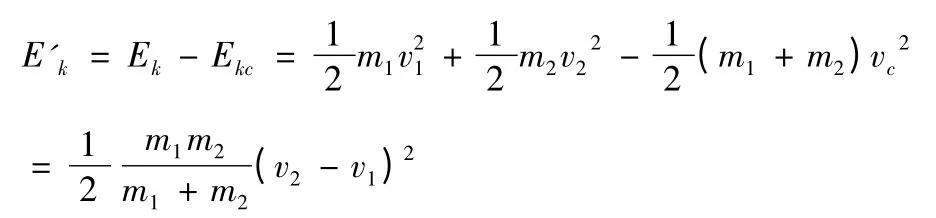
通過比較可知,在地面參照系中和質心系中人所做的功是一樣的。

