巧用平均數求解物理問題

張榮登

（云南省臨滄市雙江自治縣委黨校，云南 雙江 677300）

巧用平均數求解物理問題

張榮登

（云南省臨滄市雙江自治縣委黨校，云南 雙江 677300）

要做好物理教學工作，必須關注數學知識的應用，恰當地挖掘學生的數學知識并指導學生在物理問題中的應用是物理教師的一種必備素質。結合高中物理與數學的實際，通過巧用平均數求解物理問題，來說明物理教學如何恰當的應用數學知識，為物理教學服務。

平均數；物理；數學；圖象；知識遷移

物理教學中的概念教學、物理規律教學、實驗數據處理都必須以數學作為工具，學生數學水平如何，可以說直接關系到物理教學的成敗。物理教學中最重要的是物理概念和物理規律的教學，物理教學中，大多數概念和所有的物理規律必須用數學語言來描述。由于數學和物理有密切的關系，所以，指導學生準確而恰當地在物理中使用數學知識，是提高物理教學的方法之一，下面平均數在求解物理問題中的應用來說明：

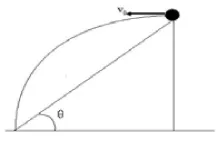
數學中，因為（a-b）2=a2-2ab+b2且（a-b）2≥0，所以a2+b2≥2ab。這樣自然得到，如果a≥0，b≥0則當且僅當a=b時取等號，稱為算術平均數，稱為幾何平均數，所以的含義是兩個不小于“0”的數的算術平均數不小于（即大于或等于）這兩個數的幾何平均數。由于，所以當a+b為定值S（即a+b=S）時，，即兩個不小于“0”的數的和為定值時這兩個數的積有最大值且僅當a=b時有最大值。且積的最大值為abmax=[2]同樣道理，當ab為定值S時，因為，即a+b≥即兩個不小于“0”的數積為定值時，這兩個數的和有最小值且僅當a=b時有最小值。最小值為以上的數學結論在物理中有重要意義，正確應用上述結論不但可使物理上的計算簡便，而且對正確理解和應用數學知識解決具體問題有重要意義。通過用數學知識解決物理問題，對培養知識的遷移能力有重要意義。下面舉幾個具體的例子加以說明。例1：某金屬帶電荷10-8庫，一與地隔緣的金屬球，與之相接觸，然后移開到相距1米的距離，問兩金屬球之間的庫侖力最大為多少牛頓？解：已知r=1米，Q1+Q2=10-8庫，求Fmax。根據庫侖定律且Q1+Q2=10-8（定值），Q1≥0，Q2≥0，，代入k、r值，牛。答：兩金屬球之間的庫侖力最大為牛頓.例2：如圖所示，斜坡長為S，斜坡高與斜坡長的比為，在坡頂以V0的水平速度拋出一物體，剛好落在坡底，問物體在做平拋運動過程中與斜面的高度最大值是多少？解：設斜坡長為S，高為h，s′為出發點到斜坡底的水平距離，根據物體在做平拋運動時有所以

在教學設計時，物理教學中恰當地指導學生應用數學知識，對于培養學生的應用知識能力是十分有益的[4]，通過這種培養，學生不但學好了物理，同時鞏固和應用了數學，這正符合知識整合的教改思想[5，6]，在新課標中是教師教學設計中必不可少的程序，也是學生必備的技能。

[1]閻金鐸.中學物理教學概論.高等教育出版社，2003年版.

[2]人民教育出版社中學數學室《數學》.人民教育社出版社，2004年版。

[3]人民教育出版社中學物理室《物理》.人民教育社出版社，2005年版。

[4]皮連生.現代教學設計.首都師范大學出版社，2005年版.

[5]王東云，楊光弟，黃銻儒.大學物理教學的學科滲透[J].高師理科學刊，2009，29（4）：91-92.

[6]楊光弟.通過學科整合提高學生能力 [J].高師理科學刊，2008，28（2）：3l.

G623

A

1674-9324（2014）22-0099-02

張榮登（1966-），男，漢族，學歷：大學本科，畢業于云南師范大學數學與應用數學專業，現從事教學與管理工作。