加油機器人操作臂的設計及運動學研究
文/祝 冉 李著信 蘇 毅
隨著我國國民經濟的飛速發展,機動車輛的數量不斷增多,許多加油站正變得不堪重負,為提高加油站的工作效率,減少污染,節省人才成本,未來將更多地使用加油機器人來完成加油工作。加油機器人由一個可移動平臺和一個操作臂組成。可移動平臺負責將整個機器人運送到需要加油的機動車位置,而操作臂則將加油槍準確地插入機動車油箱口,完成加油工作。可見,操作臂在整個系統中起著核心決定性作用。因此,本文主要針對操作臂進行研究。
1.操作臂的結構設計
操作臂是加油機器人的執行機構,要求能夠在工作空間內靈活地到達任意位置。根據實際情況,設計四自由度的操作臂如圖1所示。
該操作臂由基座1、大臂2、小臂3、手部4共四個部分以及基座關節、肩關節、肘關節、腕關節共四個關節組成。整個結構為空間關節型,四個關節均是轉動關節。其中,基座關節實現整個操作臂繞基座軸線的轉動;肩關節和肘關節帶動大臂、小臂一起作俯仰運動;作為末端執行器的加油槍固結在手部上,且加油槍的軸線與手部軸線重合,腕關節不需作搖擺運動和繞自軸的旋轉運動,只作俯仰運動。由以上四個關節即可確定加油槍相對于基座的位置與姿態。
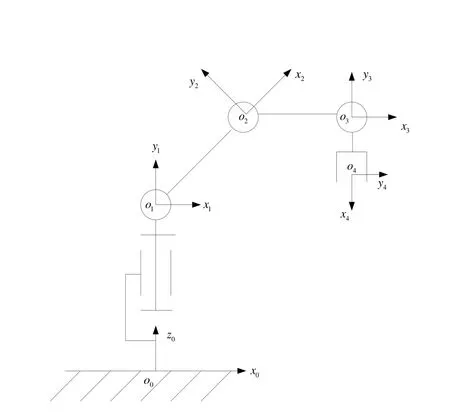
圖1 加油機器人操作臂結構簡圖及D-H坐標系
2.操作臂運動學模型的建立
Denavit和Hartenberg在1995年提出了一種對機器人進行建模的通用方法,即D-H表示法。它的核心思想是:在機器人的每個桿件上都固定一個坐標系,然后用4*4的齊次變換矩陣來表示機器人相鄰兩桿件之間的位姿關系,再通過依次變換,最終推導出機器人手部相對基座坐標系的位姿矩陣。
若用齊次坐標變換矩陣(位姿矩陣)M表示機器人手部在空間相對基座坐標系的位置和姿態,并將機器人中n個活動關節抽象為關節變量 (i=1,2,…,n),則機器人手部的位姿矩陣與關節變量之間有一定的函數,即
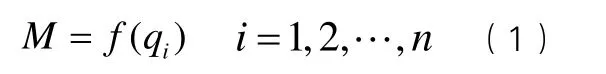
2.1 機器人運動學正問題
在式(1)中,若已知機器人各個關節變量qi,求機器人手部相對于基座坐標系的位姿M,則稱為機器人運動學正問題。
在圖1中建立桿件標準D-H坐標系,其D-H參數如表1所示。
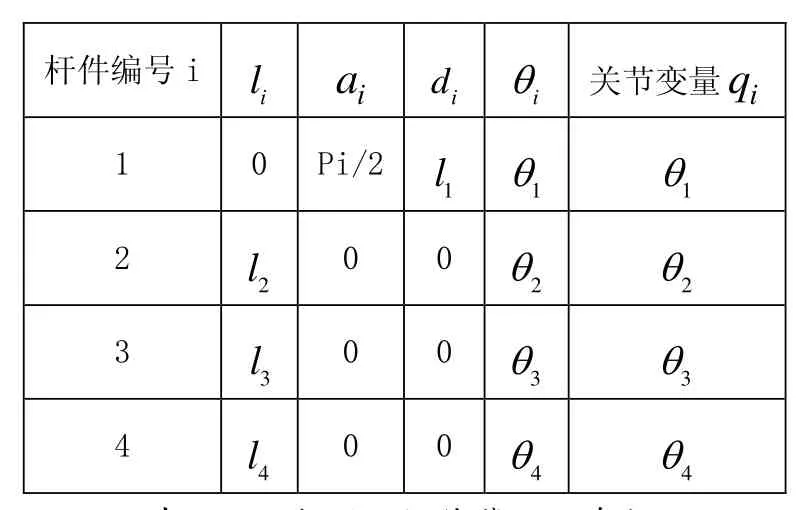
表1 加油機器人操作臂D-H參數
在每個桿件上都固定一個直角坐標系,且固定于每個桿件的上端(編號大的)關節處,桿件的編號從基座開始,基座為0號桿件,與其相連接的桿件為1號,其余依次為2,3,…,n號桿件,桿件上固結的坐標系與該桿件同號。機器人的關節編號從第一個關節開始,依次計為1,2,3,…,n。用齊次變換矩陣01M表示第1桿系相對于基座坐標系的位姿,12M表示第2桿系相對于第1桿系的位姿,表示第i桿系相對第i-1桿系的位姿,其余依次類推。
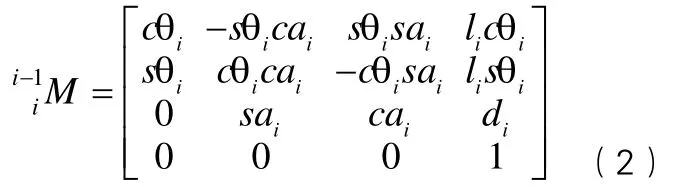
則機器人手部相對于基座坐標系的變換矩陣為:
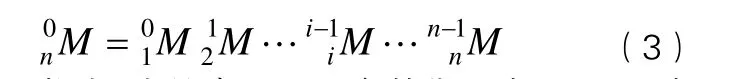
將表1中給出的D-H參數代入式(2)、式(3)中,可得加油機器人操作臂的正運動學方程
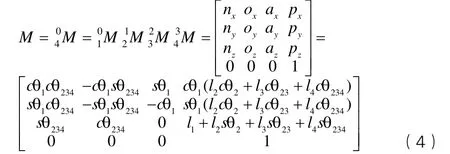
給定一組關節變量和參數的值,我們就可以利用式(4)計算出位姿矩陣中每個元素的值,得到一個唯一的位姿矩陣M。
2.2 機器人運動學逆問題
在式(1)中,若已知機器人手部相對于基座坐標系的位姿M,求機器人各個關節變量qi的值,則稱為機器人運動學逆問題。
其求解方法是利用機器人運動學方程兩端矩陣元素應相等的原理得到一組多變量的三角函數方程,通過求解這組方程來確定機器人各個關節變量的值。逆問題的解不是唯一的,當存在多個解時,應根據實際關節運動范圍的限制舍去一些解,在余下的有效解中,根據最接近原則,選取出一個最接近于當前機器人操作臂的逆解。
根據式(2)中矩陣兩邊元素相等,可建立帶有關節變量的6個函數方程(5—10):

由(5)(6)兩式可得
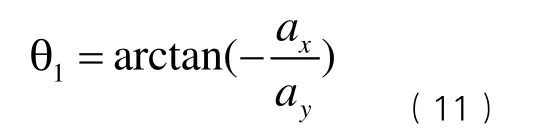
又由(7)(8)兩式可得
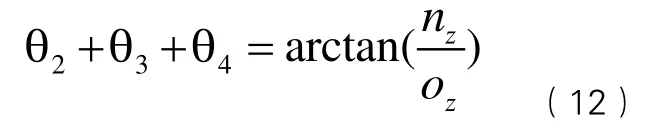
聯立(9)(10)兩式,先移項,再將其兩邊平方相加,即可解出
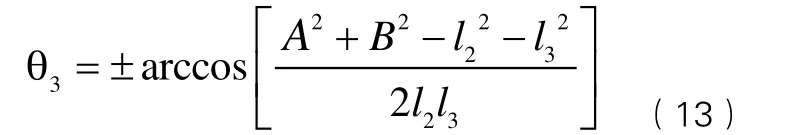
將(9)(10)兩式中的23cθ ,23sθ 展開,可得方程組
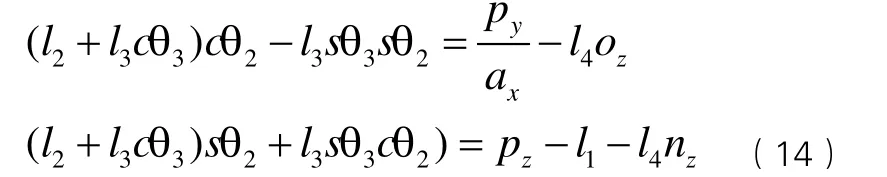
由于已知 c θ23,因此也可求得,即可將
cθ23,sθ23視為已知數代入方程組(14)中,可得
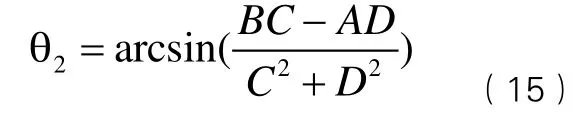
根據式(12),可得

綜上可知,式(11) 、(13)、(15)、(16)即為逆運動學方程。
3.正、逆運動學方程的驗證
通過利用MATLAB軟件中的機器人工具箱Robotics Toolbox來作計算,以此來驗證我們所建立的加油機器人操作臂正、逆運動學方程的正確性。
3.1 正運動學方程的驗證
根據實際工作情況和操作臂的工作空間限制,對各關節參數與變量賦予初值:
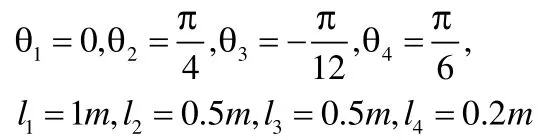
代入(4)中,得出位姿矩陣中各元素的值。

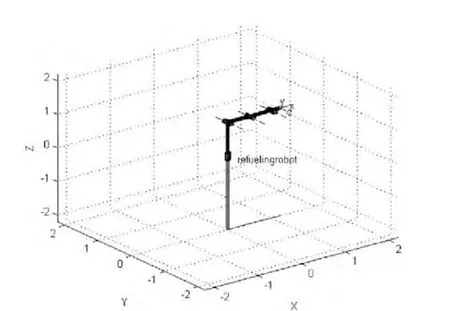
圖2 三維建模圖
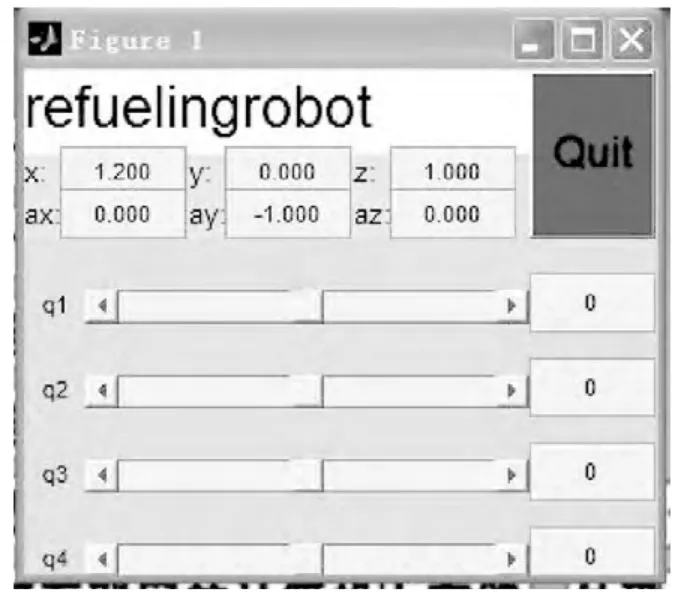
圖3 滑動控制框


可知,矩陣F中各元素的值與式(17)中各元素的值是相等的,所以加油機器人操作臂的正運動學方程是正確的。
3.2 逆運動學方程的驗證
現假設已知位姿矩陣F,我們將F中各元素的值代入式(11)、(13)、(15)、(16)中,可得兩個解
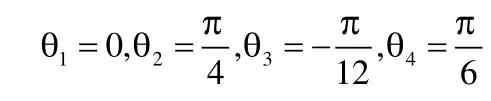
或
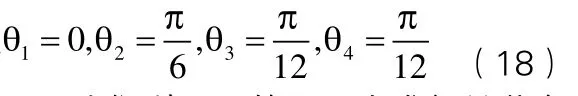
然后,我們利用函數ikine來求解關節變量
>> qr=ikine(r,F)
qr=-0.0000 0.5236 0.2618 0.2618
即qr = 0 pi/6 pi/12 pi/12
可知,我們利用MATLAB求出的解是逆方程式求出的兩個解(式18)的其中之一,所以加油機器人操作臂的逆運動學方程是正確的。
4.結束語
本文針對加油機器人操作臂進行了結構與參數設計,采用標準D-H坐標系建立了運動學方程,利用兩端矩陣元素應相等的原理求出逆解,然后以MATLAB中的Robotics Toolbox為工具,并編寫建模與計算程序,驗證了正、逆運動學方程,證明了所建立的加油機器人操作臂模型是正確的,為下一步動力學分析與軌跡規劃奠定了基礎。
[1] 朱世強,王宣銀. 機器人技術及其應用[M]. 杭州:浙江大學出版社,2001.
[2] 蔡自興. 機器人學[M]. 北京:清華大學出版社,2000.
[3] 馬香海. 機器人機構學[M].北京:機械工業出版社,1991.
[4] 景振毅,張澤兵,董霖.MATLAB 7.0實用寶典[M].北京:中國鐵道出版社,2009.
[5] 羅家佳,胡國清.基于Matlab的機器人運動仿真研究[J].廈門大學學報,自然科技版,2005,44(5):640~644.
[6] J.J.Craig.Introduction to Robotics:Mechanics and Control[M].3rd ed.New York:Prentice Hal1,2005.
[7] P. Corke.A Robotics Toolbox for MATLAB[J].IEEE Robotics and automation Magazine,1996,3(1):24~32.8.
[8] Tan J D,xiN Hybird force/position Control of mobile mampulators.IFAC,2002.

