碳約束下延時補貨庫存控制模型研究

沈 珺，桂云苗

（安徽工程大學 管理工程學院，安徽 蕪湖 241000）

如何在碳約束下調整生產存儲決策對企業運作、最優生產策略具有至關重要的影響.目前，國內外學者對碳約束下企業生產存儲決策問題進行了相應的研究［1－3］.碳排放是影響庫存模型的重要因素，目前有關庫存控制模型的文獻有很多，但涉及到碳排放卻很少［4－8］.本文希望通過參考和借鑒以往研究成果，基于延時補貨庫存模型建立考慮碳排放的庫存控制模型，為生產存儲決策提供幫助.

1 問題描述

企業在給定的政府配額內進行生產，若碳排放量超過政府配額，需從市場購買碳配額；碳排放量沒有超過政府配額，企業可將多余的碳配額在市場上出售，因此基本假設如下：

（1）考慮單一品種、連續盤點、允許延時補貨的產品庫存策略.在產品的年需求量D已知條件下，確定訂貨批量Q，并且產品生產和消耗都是勻速的，假設單位時間產品到貨量為p，單位時間產品消耗量為d.

（2）碳交易價格C，為外生變量；企業庫存總成本TC主要包括訂購成本C3、存儲成本C1和碳交易成本CX，其中假設存儲成本與平均庫存量呈線性關系，訂購成本與訂購批量無關，與訂購次數有關.

（3）在碳排放交易機制下，碳配額α由政府分配到企業，企業可在碳交易市場上買進或者賣出碳排放量X，即碳配額交易量，以彌補碳配額不足或獲得節約碳配額的交易價格.

（4）假設運輸產品所產生的碳排放量與運輸批量呈線性關系，即為e＋e0Q，其中，e是運輸工具空載時碳排放量，e0為運輸批量變動的碳排放系數.同樣假設產品存儲期間所產生的碳排放量與存儲量呈線性關系，即為g0＋gQ，其中，g0為存儲產品時固定的碳排放量，g為存儲產品變動的碳排放系數.

2 模型的建立與分析

2.1 模型的建立

碳排放市場交易機制下，企業可從市場上買賣其不足或多余的碳配額，需要考慮碳交易成本CX，因此庫存模型的總成本為：

產品運輸過程中，碳排放量與運輸產品的批量有關，即（e＋e0Q）（D/Q）；存儲時碳排放量為g0＋g（（p－dQ2p 因此運輸和存儲過程中，碳排放總量為：

不考慮碳排放或碳交易價格過高時，最優訂購量為碳排放量最小時的量，對式（4）中Q求極值，得出

對式（4）進行化簡，碳配額等于運輸和存儲過程中產生的碳排放量與碳配額交易量之和，即為：

為了計算的方便性，不考慮常量，令e0＝g0＝0，則

將式（7）代入式（3），得出延時補貨庫存模型的總成本為：

對式（8）中Q求解，得出考慮碳排放時延時補貨庫存控制模型的最優訂購量為：

2.2.2 對蘇丹草全磷的影響 不同接種劑對蘇丹草全磷含量均有影響，全磷含量由高至低的處理依次為F5>F6>MR>F1>F4>F3>CK>P>F2。各接種劑處理(除P、F2外)較CK全磷含量可提高6.7%～26.7%，F2最低為0.26%，F5含量最高，為0.38%，F5與CK存在顯著差異(P<0.05)，其余處理均與CK差異不顯著(圖2-B)。

將式（9）的Q＊代入式（8），得出考慮碳排放時延時補貨庫存控制模型的最低總成本為：

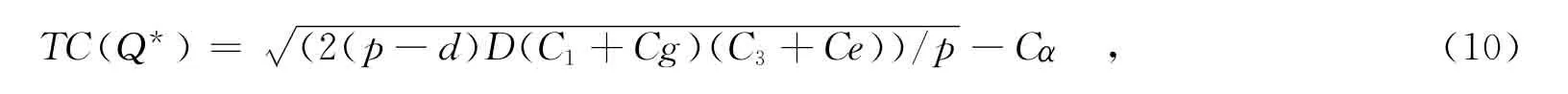
2.2 兩類庫存模型的比較分析

為了進一步分析兩種情形下庫存模型對企業庫存決策的影響，本文從最優訂貨量、碳交易價格、碳配額等角度比較兩類庫存模型，可得命題1～4.

命題1 （1）若C1/C3＜g/e，那么Q0＞Q＊＞；（2）若C1/C3＞g/e，那么若C1/C3＝g/e，那么Q＊＝Q0＝.

命題2 碳配額α固定不變下，若碳交易價格C增加，則：（1）若C1/C3＜g/e，最優訂購量Q*，碳排放總量CF減少；碳配額交易量X增加；（2）若C1/C3＞g/e，最優訂購量Q＊，碳配額交易量X增加；碳排放總量CF減少；（3）若C1/C3＝g/e，最優訂購量Q＊、碳排放總量CF、碳配額交易量X保持不變；（4）若α≤總成本TC（Q＊）增加總成本減少；（C1e＋C3g）總成本先增加后減少.

證明 （1）由式（4）得，d（Q＊）/dc＝pD（eC1－gC3）/（p－d）Q＊（C1＋Cg）2，dCF（Q＊）/dc＝gp（Q＊2－）/2Q＊2（p－d），當g/e≠C3/C1時，dCF（Q）/dC ＜0，當g/e＝C3/C1時，dCF（Q）/dC＝0.

由命題1可知，存儲成本與訂購成本的比值等于存儲與運輸所產生的碳排放量的比值時，兩類庫存模型的最優訂購量相同，企業不需要考慮碳約束；當存儲成本與訂購成本的比值小于存儲與運輸所產生的碳排放量的比值時，不考慮碳排放的最優訂購量大于考慮碳排放時最優訂購量，企業可訂購少量的產品保持較少的庫存，反之亦然.由命題2可知，隨著碳交易價格增加，當存儲成本與訂購成本的比值等于存儲與運輸產生碳排放量的比值且碳配額較大時，兩類庫存模型的最優訂購量、碳配額交易量、碳排放總量相同，總成本隨之減少；當存儲成本與訂購成本的比值小于存儲與運輸產生碳排放量的比值且碳配額較小時，最優訂購量減少，總成本增加；當存儲成本與訂購成本的比值大于存儲與運輸產生碳排放量的比值且碳配額適中時，最優訂購量增加，總成本先增加隨后減少.

命題3 碳交易價格固定不變下，若碳配額α增加，則：（1）最優訂購量和碳排放總量保持不變；（2）碳配額交易量X增加，總成本TCQ減少.

命題4 （1）碳排放市場交易機制引導企業減少了碳排放量.（2）當總成本TC（Q＊）＞TC0；當如C＜ （（2D（pd）（C1e＋C3g））/p－2α則TC（Q＊）＞TC0；如C＞（（2D（p－d）（C1e＋C3g））/p－2α則TC（Q＊）＜TC0；當α≥ （C1e＋C3g）總成本TC（Q＊）＞TC0；（3）當X＞0，TC（Q＊）＞TC.

證明 （1）ΔCO2＝［eD/Q0＋g（p－d）Q0/2p］－［eD/Q＊－g（p－d）Q＊/2p］，由命題1得知，當C1/C3≠g/e時，ΔCO2＞0，當C1/C3＝g/e時，CO2＝0.

（2） 增 加 的 成 本.ΔTC＝TC（Q＊） －TC0＝

由此可見，當碳排放量超過政府配額時，企業可在市場上購進碳配額；若碳排放量沒有超過政府配額，企業可出售多余的碳配額獲得收益，因此碳排放市場交易機制引導企業減少了碳排放量.命題4（2）表明企業在某些特殊情況下可同時減少碳排放量和總成本.

3 算例分析

為了直觀地驗證前面結論的有效性，本文用具體數值分析參數變化對決策的影響，假設D＝72 000，p＝12 000，d＝6 000，C＝0.3，α＝9 000，其余數據C3、C1、e、g如表1所示，利用 Mathmatica 5.2軟件得出計算結果如表1所示.從表1的計算結果得知，當存儲成本與訂購成本的比值和運輸與存儲產生的碳排放量的比值不等時，最優訂購量介于不考慮碳排放時最優訂購量和碳排放量最小時的最優訂購量之間.當碳配額低于一個臨界值時，企業在市場上購進不足的碳配額，成本隨之增加；高于一個臨界值時，企業出售多余的碳配額獲得收益.

表1 模型的數值計算

碳配額對碳配額交易量和最優訂購量的影響如圖1所示.碳交易價格對總成本和最優訂購量的影響圖如圖2所示.其中當存儲成本與訂購成本的比值小于存儲與運輸產生碳排放量的比值且碳配額較小時，如圖2a所示；當存儲成本與訂購成本的比值大于存儲與運輸產生碳排放量的比值且碳配額適中時，如圖2b所示；當存儲成本與訂購成本的比值等于存儲與運輸產生碳排放量的比值且碳配額較大時，如圖2c所示.圖1表明企業的最優訂購量與碳配額無關，碳配額交易量與碳配額有關，隨著碳配額增加，碳配額交易量增加.圖2表明隨著碳交易價格增加，當存儲成本與訂購成本的比值等于存儲與運輸產生碳排放量的比值且碳配額較大時，碳交易價格不影響最優訂購量，總成本隨之減少；當存儲成本與訂購成本的比值小于存儲與運輸產生碳排放量的比值且碳配額較小時，最優訂購量減少，總成本增加；當存儲成本與訂購成本的比值大于存儲與運輸產生碳排放量的比值且碳配額適中時，最優訂購量增加，總成本先增加隨后減少.

圖1 碳配額對碳配額交易量和最優訂購量的影響

圖2 碳交易價格對總成本和最優訂購量的影響

4 結束語

研究了碳約束下延時補貨庫存控制模型問題，對不考慮及考慮碳排放情況下兩類庫存模型的比較分析得出兩者最優訂購量和總成本在不同環境下發生的變化.碳排放市場交易機制有效地引導企業減少碳排放量，同時企業的最優訂購量取決于臨界值的大小，碳配額的變化會對總成本產生影響，企業可在市場上出售多余的碳配額獲得收益.最后通過算例分析證明參數變化對企業決策的影響，本文幫助企業管理者在不同經濟情況下調整最優訂購量，為管理者在生產存儲決策上提供支持和幫助，同時對于實現低碳戰略具有重要的理論意義和現實意義.本文只涉及需求確定的情形，對于需求不確定情況下碳約束庫存模型的相關問題有待后繼研究.

［1］ 杜少甫.考慮排放許可與交易的生產優化［J］.中國管理科學，2009，17（3）：81－86.

［2］ 范體軍，楊鑒.碳排放交易機制下減排技術投資生產庫存［J］.北京理工大學學報，2012，12（6）：14－21.

［3］ Park Hojeong，Lim Jaekyu.Valuation of marginal CO abatement options for electric power plants in Korea［J］.Energy Policy，2009，37（5）：1 834－1 841.

［4］ Kimns，Janic，Bvanwee.Trade－off between carbon dioxide emissions and logistics costs based on Multiobjective optimization［J］.Transportation Research Record，2009，39（1）：107－116.

［5］ Sundarakanib，Rdesouza，Mgoh.Modeling carbon footprints across the supply chain［J］.International Journal of Production Economics，2010，128（1）：43－50.

［6］ Piecyk，Mckinnon.Forecasting the carbon footprint of road freight transport in 2020［J］.International Journal of Production Economics，2010，128（1）：31－42.

［7］ 方健，徐麗群.考慮碳排放的物流網絡庫存成本控制模型研究［J］.科技管理研究，2012（2）：232－240.

［8］ Weihua G，Cheng T.Managing carbon footprints in inventory management［J］.International Journal of Production E－conomy，2011，132（2）：178－185.