基于雷達(dá)距離像的錐體目標(biāo)進(jìn)動(dòng)參數(shù)估計(jì)方法

寧超，黃璟，朱勇，肖志河

(電磁散射重點(diǎn)實(shí)驗(yàn)室, 北京 100854)

0 引言

空間目標(biāo)的微運(yùn)動(dòng)是指其整體或部件除質(zhì)心平動(dòng)以外的振動(dòng)、轉(zhuǎn)動(dòng)等微小運(yùn)動(dòng)。微動(dòng)在雷達(dá)回波中產(chǎn)生的多普勒稱為微多普勒[1-2]。進(jìn)動(dòng)是中段彈頭特有的微動(dòng)方式，與目標(biāo)形狀結(jié)構(gòu)、質(zhì)量分布和動(dòng)力學(xué)特性等物理屬性密切相關(guān)。進(jìn)動(dòng)作為一種分辨真假目標(biāo)的特征，受到廣泛關(guān)注。有研究表明，彈道中段，彈頭和誘餌的姿態(tài)運(yùn)動(dòng)差異較大，主要體現(xiàn)在進(jìn)動(dòng)周期、進(jìn)動(dòng)角等微動(dòng)參數(shù)上，微動(dòng)特征為非合作空間目標(biāo)探測(cè)與分類識(shí)別提供了一條可行的途徑，也成為了彈道中段目標(biāo)識(shí)別研究的熱點(diǎn)領(lǐng)域之一[3-5]。

彈道目標(biāo)進(jìn)動(dòng)的進(jìn)動(dòng)特征主要包括進(jìn)動(dòng)周期和進(jìn)動(dòng)角。對(duì)于進(jìn)動(dòng)周期提取相對(duì)容易，而進(jìn)動(dòng)角特征提取難度大。國(guó)內(nèi)，國(guó)防科技大學(xué)、西安電子科技大學(xué)、航天科工集團(tuán)等多家單位開展了相關(guān)的研究，主要方法包括基于RCS幅度的提取方法、基于頻譜特征的提取方法、基于雷達(dá)高分辨距離像的提取方法等，已有多篇文章文獻(xiàn)刊出[6-9]。其中，文獻(xiàn)[6]中提出了一種利用目標(biāo)RCS的幅度值作為特征估計(jì)彈道目標(biāo)的進(jìn)動(dòng)角的方法，而對(duì)于非合作目標(biāo)難以預(yù)先獲得其精確的RCS。文獻(xiàn)[7]提出了利用時(shí)頻分析提取進(jìn)動(dòng)參數(shù)的方法，但僅適用于目標(biāo)零攻角飛行的情況。文獻(xiàn)[8]提出用一維距離像序列估計(jì)進(jìn)動(dòng)參數(shù)，其方法也需要預(yù)知目標(biāo)尺寸等作為先驗(yàn)信息。

本文提出了基于寬帶雷達(dá)一維距離像的非合作錐體目標(biāo)微動(dòng)參數(shù)提取的新方法。首先得到目標(biāo)的一維距離像(high resolution range profile，HRRP)時(shí)間序列，再根據(jù)雷達(dá)測(cè)軌信息，估計(jì)得到彈道中段目標(biāo)的質(zhì)心位置，聯(lián)合使用目標(biāo)質(zhì)心位置與HRRP的徑向長(zhǎng)度特征，使用分步全局最優(yōu)估計(jì)算法得到飛行進(jìn)動(dòng)錐體的長(zhǎng)度、底面半徑、進(jìn)動(dòng)角、進(jìn)動(dòng)周期等參數(shù)。該方法需要的先驗(yàn)信息少，對(duì)于非合作目標(biāo)有較好的適用性。文中通過仿真數(shù)據(jù)驗(yàn)證了方法的可行性和正確性。

1 飛行中段進(jìn)動(dòng)目標(biāo)HRRP徑向長(zhǎng)度特征

飛行中段的進(jìn)動(dòng)錐體目標(biāo)的運(yùn)動(dòng)可以看作2種運(yùn)動(dòng)的合成：一是質(zhì)心的平動(dòng)，由天體力學(xué)可知，在近似真空的環(huán)境中僅受萬(wàn)有引力的作用，其運(yùn)動(dòng)軌跡為橢圓，該橢圓的一個(gè)焦點(diǎn)為地心，橢圓所在平面被稱為飛行彈道面；另一種運(yùn)動(dòng)是錐體的進(jìn)動(dòng)，即由于初始沖量力矩的影響，產(chǎn)生的以固定的角速度繞其質(zhì)心錐旋和自旋，本文考慮理想錐體目標(biāo)，不考慮自旋對(duì)雷達(dá)回波影響。接下來(lái)，分2步進(jìn)行討論：先忽略平動(dòng)，分析固定質(zhì)心的進(jìn)動(dòng)對(duì)雷達(dá)回波的影響；然后再疊加平動(dòng)，分析飛行中進(jìn)動(dòng)錐體的雷達(dá)回波特征。

1.1 固定質(zhì)心的進(jìn)動(dòng)目標(biāo)HRRP徑向長(zhǎng)度特征

考慮均勻的軸對(duì)稱，長(zhǎng)度為l，進(jìn)動(dòng)中心距離球頂為h，底面半徑為b。設(shè)進(jìn)動(dòng)角為γ，進(jìn)動(dòng)速率ω，雷達(dá)視線與進(jìn)動(dòng)軸夾角為β。如圖1所示。

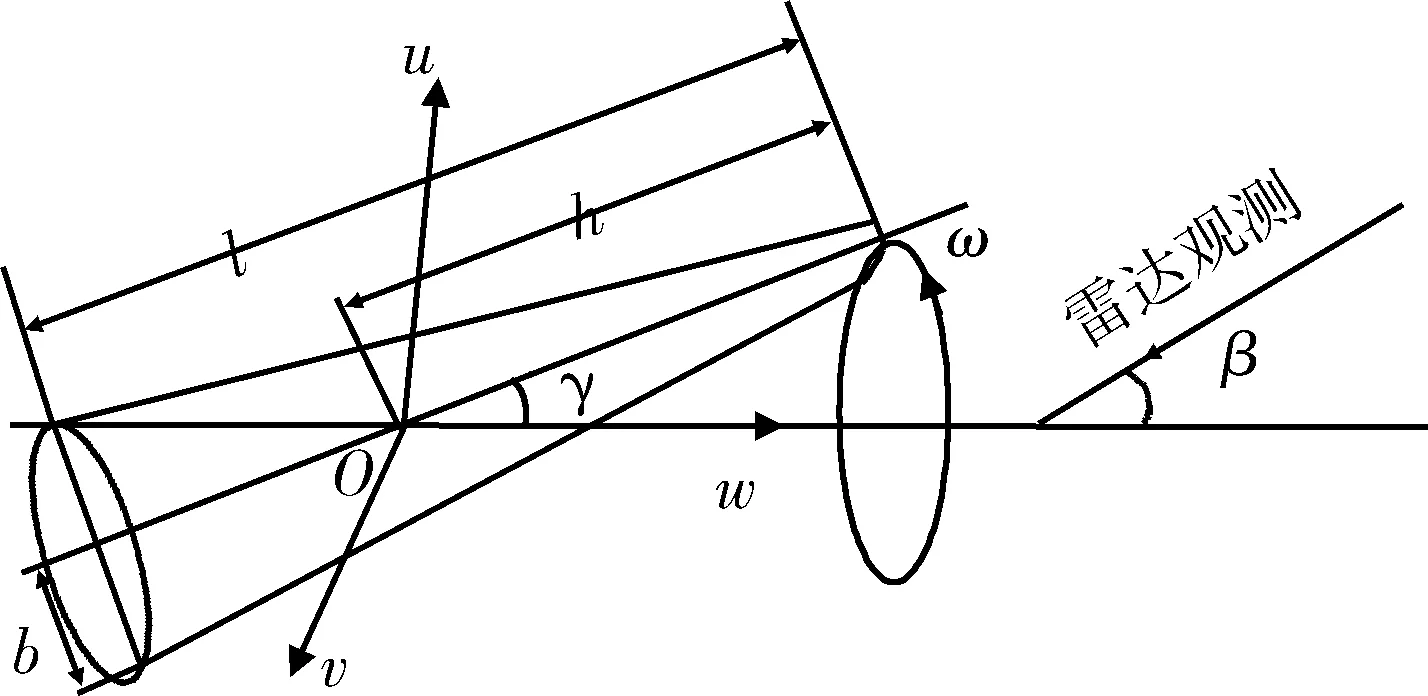
圖1 雷達(dá)觀測(cè)固定質(zhì)心的進(jìn)動(dòng)錐體Fig.1 Stationary precession cone in radar sight

建立進(jìn)動(dòng)的坐標(biāo)系Ouvw，設(shè)進(jìn)動(dòng)軸為w軸，將雷達(dá)視線與進(jìn)動(dòng)軸組成的平面定義為Ouw面，根據(jù)右手螺旋法則確定v軸指向。則進(jìn)動(dòng)錐體的對(duì)稱軸的指向可表示為

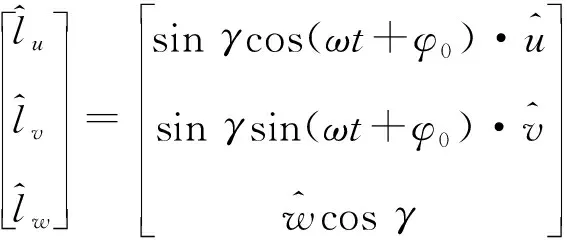
(1)

式中：φ0為觀測(cè)0時(shí)刻的進(jìn)動(dòng)轉(zhuǎn)角。

雷達(dá)視線矢量方向?yàn)?/p>

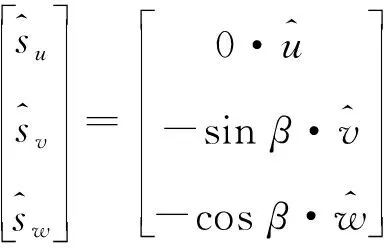
(2)

定義雷達(dá)視線與錐體對(duì)稱軸的夾角為雷達(dá)視線角，記為α(t)，有

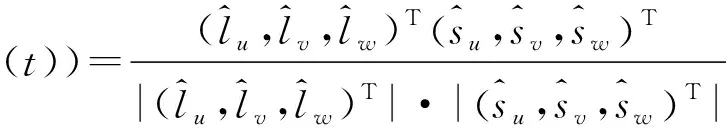
(3)

α(t)=arccoscosβcosγ+sinβsinγcos(ωt+φ0).

(4)

由空間幾何關(guān)系和電磁散射特性的知識(shí)可得，錐體有兩個(gè)強(qiáng)散射中心，分別在球頂和棱邊[10]，錐體的HRRP長(zhǎng)度可表示為

L(t)=lcos(α(t))-bsin(α(t)).

(5)

由式(4)，固定質(zhì)心的進(jìn)動(dòng)目標(biāo)一維距離像的徑向長(zhǎng)度呈周期性變化，令

(6)

tanη=b/l.

(7)

式(5)可變換為

L(t)=l′cos(η+α(t)).

(8)

則HRRP最小為

Lmin=l′cosβ+γ+η.

(9)

HRRP最大為

Lmax=l′cosβ-γ+η.

(10)

1.2 運(yùn)動(dòng)質(zhì)心的進(jìn)動(dòng)目標(biāo)HRRP徑向長(zhǎng)度特征

中段飛行的彈道導(dǎo)彈目標(biāo)，當(dāng)完成軌道修正和誘餌釋放后，控制系統(tǒng)會(huì)調(diào)整彈頭指向保證其最佳再入角，所以在不考慮飛行誤差的情況下，可以認(rèn)為中段飛行的中后期，目標(biāo)的進(jìn)動(dòng)軸在彈道平面內(nèi)，且指向固定[6]。如圖2所示。錐體沿彈道飛行，雷達(dá)視線與進(jìn)動(dòng)軸夾角是變化的，同時(shí)進(jìn)動(dòng)也導(dǎo)致了錐體軸指向的改變，上述2種運(yùn)動(dòng)共同引起了錐體雷達(dá)視線角的改變。

描述飛行的進(jìn)動(dòng)錐體雷達(dá)視線角隨時(shí)間的變化，定義2個(gè)坐標(biāo)系，雷達(dá)坐標(biāo)系Oxyz和進(jìn)動(dòng)坐標(biāo)系O′uvw。進(jìn)動(dòng)坐標(biāo)系的定義同前節(jié)，設(shè)進(jìn)動(dòng)軸為O′w軸，并將觀測(cè)0時(shí)刻的雷達(dá)視線與進(jìn)動(dòng)軸組成平面定義為O′uw面。

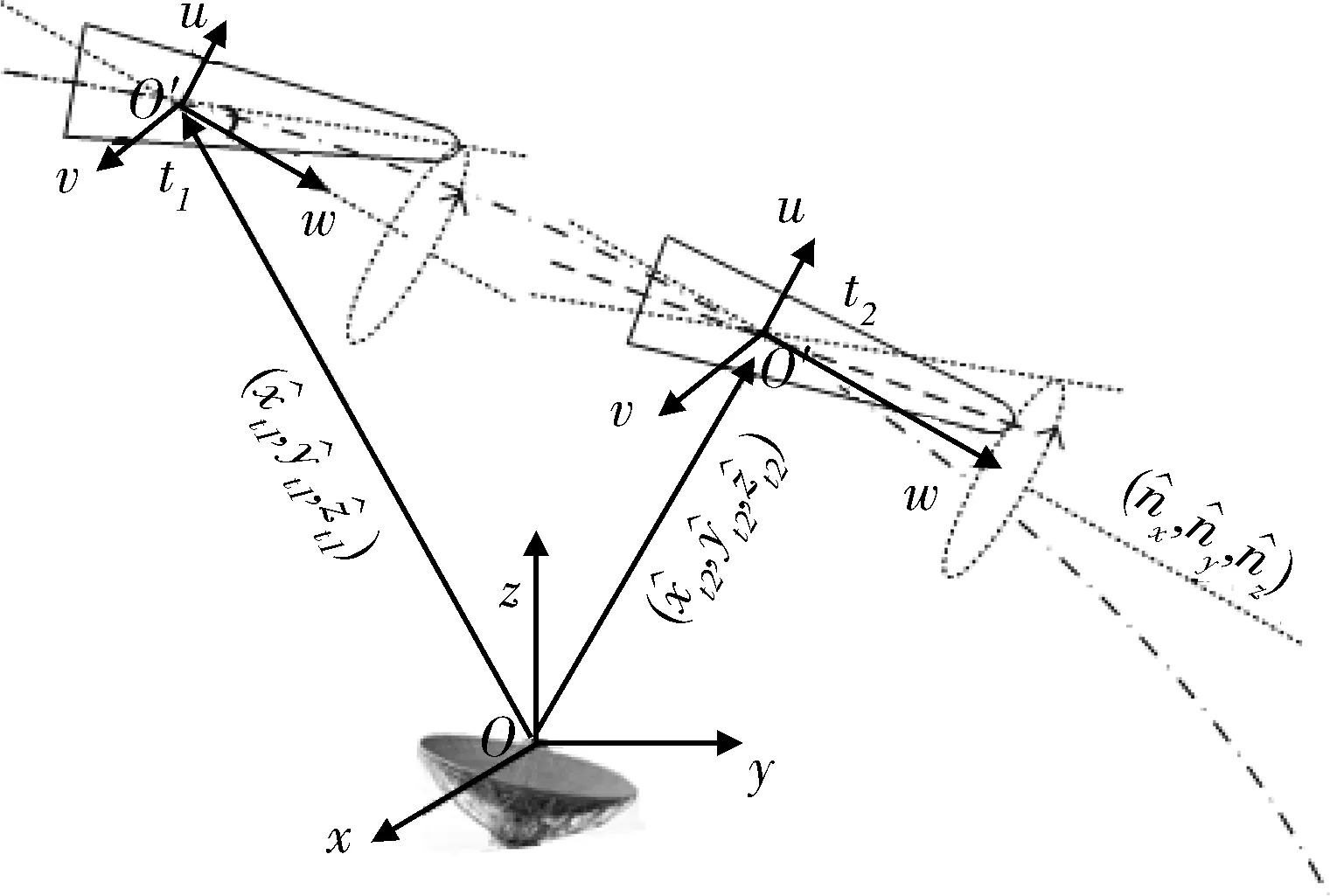
圖2 飛行的進(jìn)動(dòng)錐體示意圖Fig.2 Geometry of flying precession cone

(11)

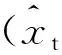
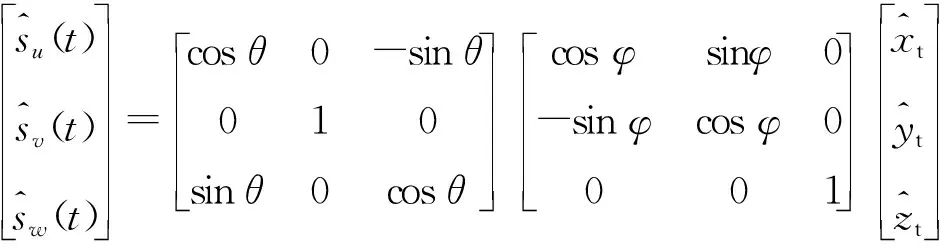
(12)

則進(jìn)動(dòng)錐體的對(duì)稱軸的方向矢量仍可表示為式(1)。將式(12)代入式(3)和(5)即可得到飛行的錐體的HRRP徑向長(zhǎng)度表達(dá)式：

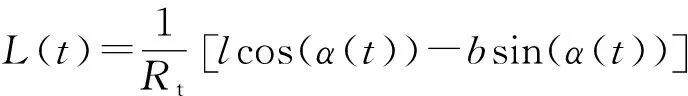
(13)

cos(α(t))=atsinγcos(ωt+φ0)-

btsinγsin(ωt+φ0)+

ctcosγ.

(14)

式中：

(15)

設(shè)錐體長(zhǎng)度為l=4 m，b=0.5 m，進(jìn)動(dòng)角為γ=10°，進(jìn)動(dòng)速率ω=2π，進(jìn)動(dòng)軸在雷達(dá)坐標(biāo)系中θ=20°，φ=30°，又設(shè)飛行錐體的初始質(zhì)心位置坐標(biāo)為(x,y,z)=(200,50,200)km勻速飛行速度為(vx,vy,vz)=(-6,0,-4)km/s，并設(shè)φ0=0，計(jì)算得到HRRP徑向長(zhǎng)度如圖3所示。進(jìn)動(dòng)引起HRRP徑向長(zhǎng)度的起伏，但由于飛行的影響，周期不再是常量，HRRP徑向長(zhǎng)度的極大值和極小值也隨飛行時(shí)刻而改變。徑向長(zhǎng)度隨時(shí)間的改變?yōu)檫M(jìn)動(dòng)參數(shù)的估計(jì)提供了條件。

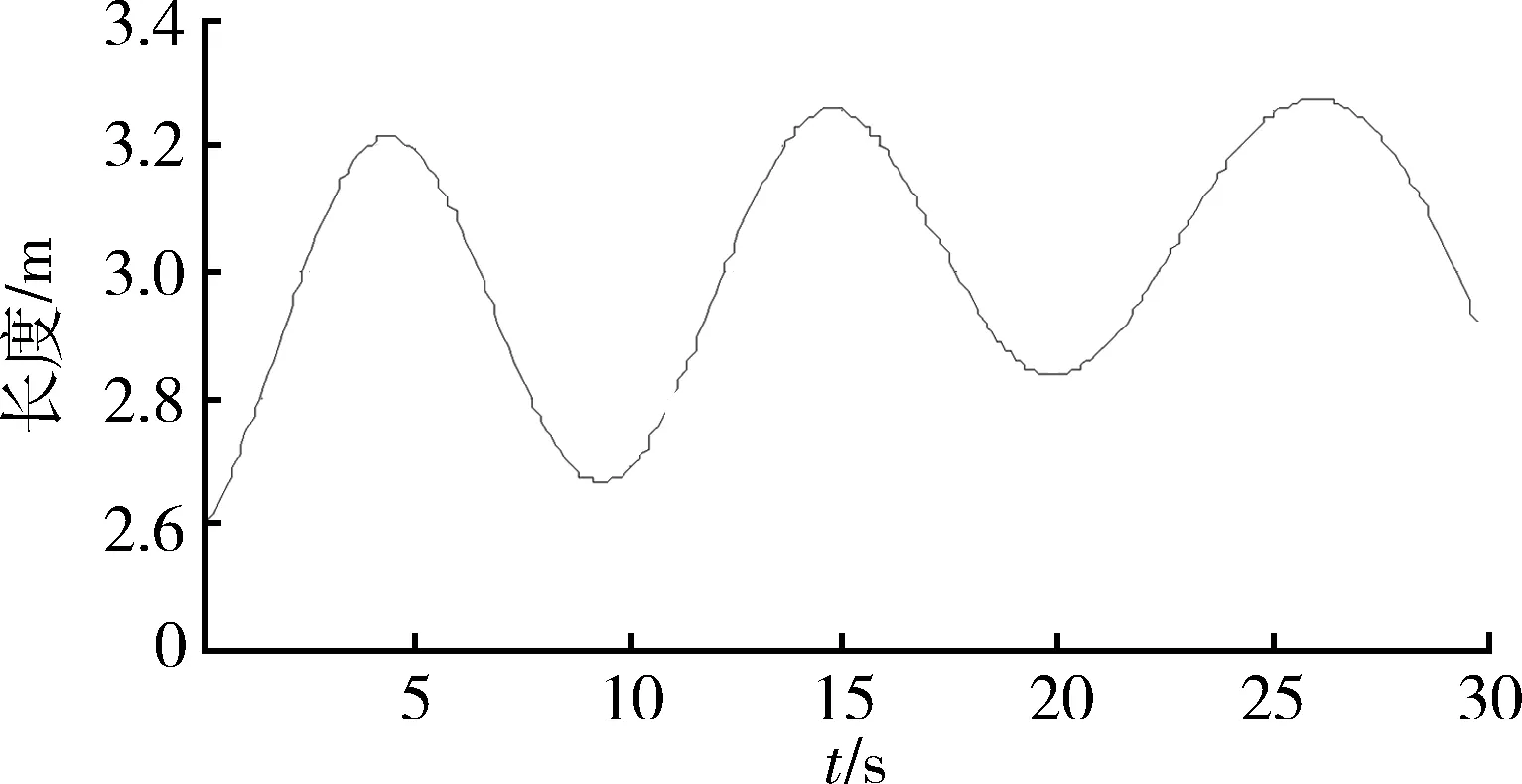
圖3 飛行進(jìn)動(dòng)錐體的HRRP徑向長(zhǎng)度Fig.3 HRRP length of flying precession cone

2 飛行進(jìn)動(dòng)錐體目標(biāo)的微動(dòng)參數(shù)估計(jì)

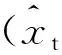
min(max)f(x)，s.t.x∈S.

(16)

對(duì)應(yīng)于本文的數(shù)學(xué)模型，最優(yōu)估計(jì)表達(dá)式為

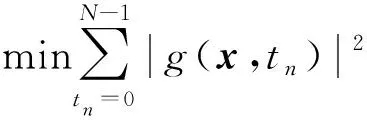
(17)

式中：

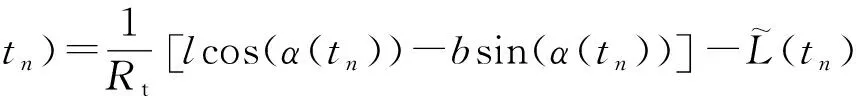
(18)

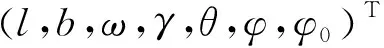
(19)

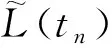
式(18)中有2個(gè)三角函數(shù)，且未知量多，計(jì)算復(fù)雜，直接估計(jì)困難大。為了提高估計(jì)效率，減小計(jì)算難度，本文采用分步全局最優(yōu)估計(jì)法：首先將數(shù)學(xué)模型簡(jiǎn)化初估，得到未知量的粗估值；再將粗估值作為二次估計(jì)的初值，并進(jìn)一步縮小各參數(shù)搜索范圍后，利用精確模型再次優(yōu)化，最終得到的未知量精確解。

模型的簡(jiǎn)化過程為：對(duì)于錐體，當(dāng)l?b，且從頭部附近觀測(cè)時(shí)有

L(t)≈lcos(α(t)).

(20)

所以可近似簡(jiǎn)化為

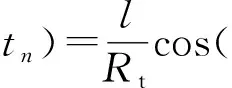
(21)

與原數(shù)學(xué)模型相比，新模型少了一個(gè)未知量，而且方程中只剩一個(gè)的三角函數(shù)的計(jì)算，估計(jì)更容易。

利用(21)得到x的初步估計(jì)后，根據(jù)粗估值，縮小搜索范圍，通過精確模型(18)進(jìn)行二次估計(jì)，得到最終結(jié)果。為了避免最優(yōu)解中存在局部最優(yōu)的問題，一方面根據(jù)參數(shù)的物理意義，增加約束條件，限制其值域；另一方面可采取變換初值多次估計(jì)的方法，以確保結(jié)果的準(zhǔn)確。

綜上，對(duì)飛行進(jìn)動(dòng)錐體的微動(dòng)參數(shù)估計(jì)的具體步驟為：

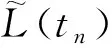
(2) 利用簡(jiǎn)化的HRRP徑向長(zhǎng)度模型式(20)對(duì)(14)和(15)中的參數(shù)粗估計(jì)；

(3) 利用參數(shù)粗估計(jì)的結(jié)果，縮小參數(shù)的搜索范圍；

(4) 利用精確表達(dá)式(13)進(jìn)行二次全局優(yōu)化，估計(jì)得到進(jìn)動(dòng)參數(shù)的估計(jì)值。

3 仿真結(jié)果及分析

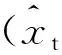
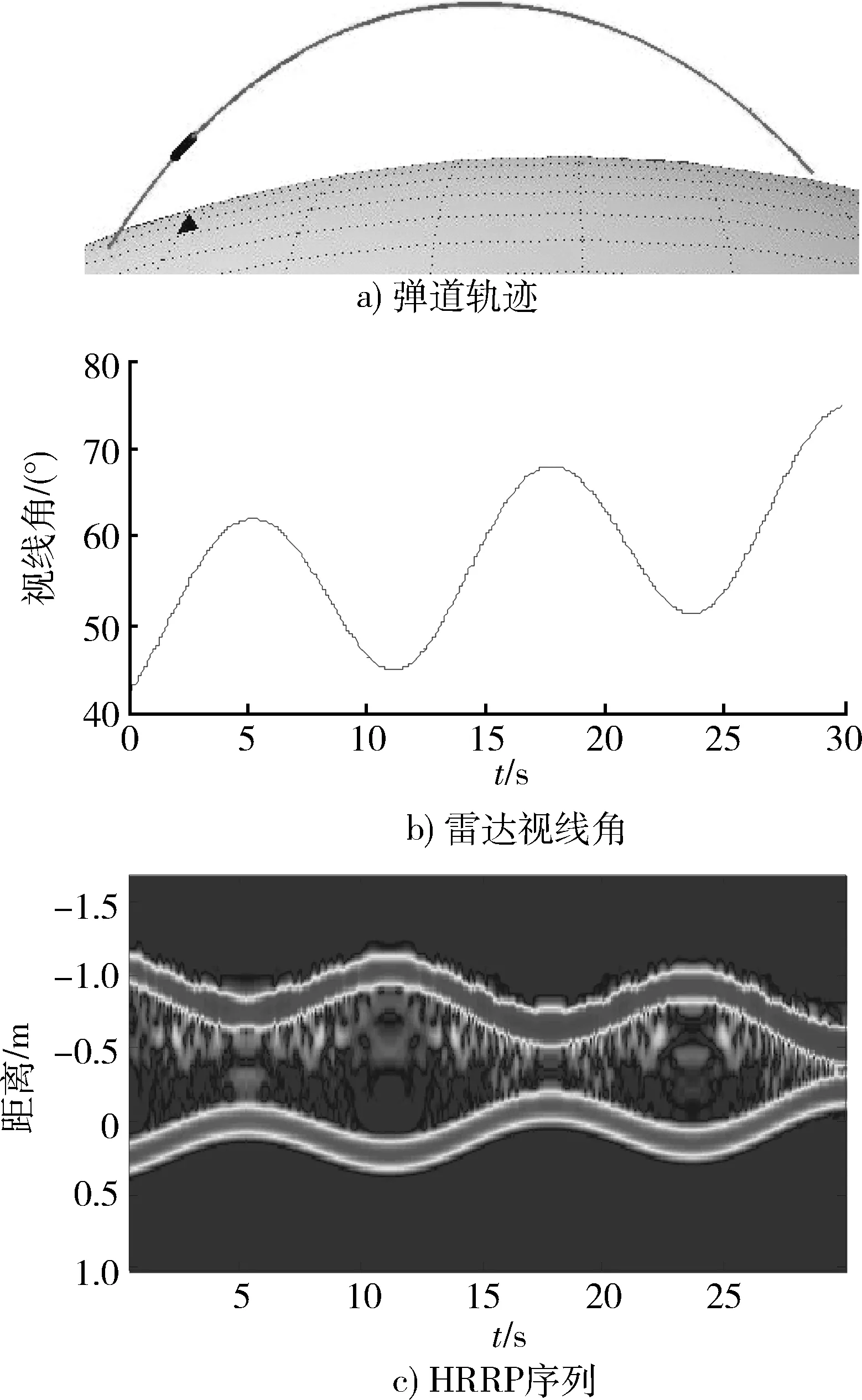
圖4 仿真結(jié)果Fig.4 Simulated results

表1 微動(dòng)參數(shù)估計(jì)結(jié)果Table 1 Estimated results of precession parameters

進(jìn)動(dòng)角/(°)進(jìn)動(dòng)周期/s圓錐高度/m底面半徑/m9.9112.534.010.36

仍利用上述彈道和雷達(dá)參數(shù)，改變進(jìn)動(dòng)角和進(jìn)動(dòng)周期，估計(jì)的結(jié)果如表2所示。

由表2，本文方法能夠在不同進(jìn)動(dòng)狀態(tài)下對(duì)進(jìn)動(dòng)參數(shù)進(jìn)行估計(jì)。對(duì)進(jìn)動(dòng)角、進(jìn)動(dòng)周期、圓錐高度的估計(jì)效果好，誤差均小于10%。其中進(jìn)動(dòng)周期的估計(jì)準(zhǔn)確度最好，對(duì)進(jìn)動(dòng)角和圓錐高度估計(jì)的準(zhǔn)確度次之，而對(duì)底面半徑的估計(jì)效果較差。

分析其原因?yàn)椋河捎诶走_(dá)帶寬的限制，HRRP徑向長(zhǎng)度提取存在誤差。徑向長(zhǎng)度的誤差會(huì)導(dǎo)致進(jìn)動(dòng)參數(shù)的誤差。該誤差對(duì)周期參數(shù)的影響最小，故對(duì)周期的估計(jì)效果最好。而根據(jù)第2節(jié)分析，錐體的底面半徑對(duì)HRRP徑向長(zhǎng)度的影響很小，近似可以忽略；所以利用HRRP長(zhǎng)度反推底面半徑時(shí)，精度也不高。

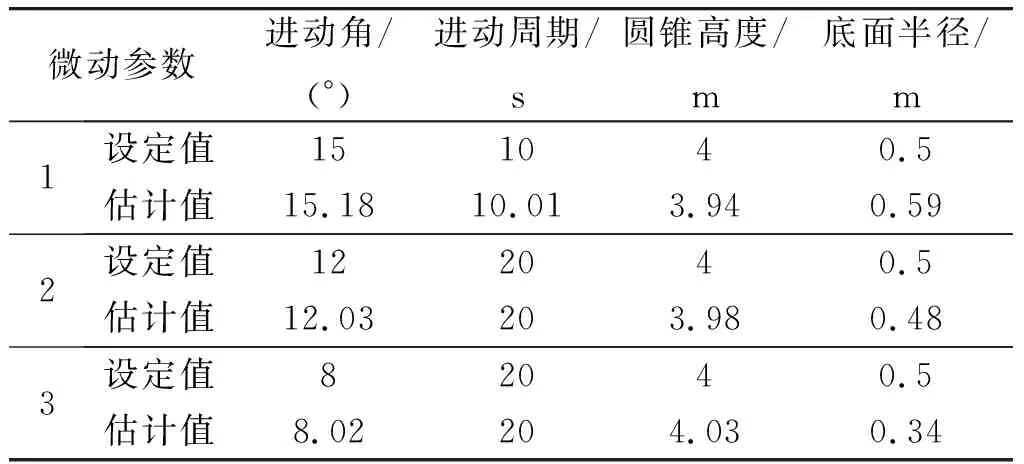
表2 不同參數(shù)微動(dòng)參數(shù)估計(jì)結(jié)果Table 2 Estimated results of several precession parameters

4 結(jié)束語(yǔ)

本文提出了一種基于HRRP時(shí)間序列和雷達(dá)測(cè)軌信息的飛行進(jìn)動(dòng)錐體目標(biāo)微動(dòng)參數(shù)的估計(jì)方法，能夠正確估計(jì)進(jìn)動(dòng)角、進(jìn)動(dòng)周期、錐體高度等參數(shù)，上述參數(shù)可以作為識(shí)別特征量用于目標(biāo)的分類識(shí)別。仿真結(jié)果證明了方法的可行性和正確性。該方法可以應(yīng)用于特征提取和目標(biāo)識(shí)別領(lǐng)域。文中仿真計(jì)算未討論雷達(dá)測(cè)量誤差等不確定因素，在后續(xù)工作中還需要進(jìn)一步研究雷達(dá)測(cè)量誤差和信噪比等對(duì)估計(jì)精度的影響。

參考文獻(xiàn)：

[1] 周萬(wàn)幸. 彈道導(dǎo)彈雷達(dá)目標(biāo)識(shí)別技術(shù)[M].北京：電子工業(yè)出版社，2011.

ZHOU Wan-xing. BMD Radar Target Recongnition Technology[M].Beijing:Publishing House of Electronics Industry, 2011.

[2] CHEN V C, LI Fa-yin, Shen-Shyang Ho, et al.Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study[J]. IEEE , 2006,42(1)：2-21.

[3] 李松，馮有前，劉昌云,等. 彈道導(dǎo)彈微動(dòng)模型及微多普勒特征研究[J]. 現(xiàn)代防御技術(shù)，2011，39(6)：95-100.

LI Song, FENG You-qian, LIU Chang-yun, et al. Research of Micro-Motion Model and Micro-Doppler of Ballistic Missile[J]. Modern Defence Technology, 2011, 39(6):95-100.

[4] 馬梁，王雪松，李永禎，等. 雷達(dá)部署對(duì)進(jìn)動(dòng)目標(biāo)微多普勒頻率的可測(cè)性分析[J]. 國(guó)防科技大學(xué)學(xué)報(bào)，2011(4)：54-59.

MA Liang, WANG Xue-song, LI Yong-zhen, et al. Influence of Radar Location on the Measurability of Micro-doppler Detecting for Precession Target[J]. Journal of National University of Defense Technology, 2011(4): 54-59.

[5] 高紅衛(wèi)，文樹梁，謝良貴. 雷達(dá)脈沖串波形下的目標(biāo)微動(dòng)特征提取[J]. 現(xiàn)代防御技術(shù)，2009，37(5)，132-135.

GAO Hong-wei, WEN Shu-liang, XIE Liang-gui. Target Micromotion Feature Extraction from Radar Pulse Train Waveform[J]. Modern Defence Technology, 2009, 37(5), 132-135.

[6] 陳行勇，黎湘，郭桂榮,等. 微進(jìn)動(dòng)彈道導(dǎo)彈目標(biāo)雷達(dá)特征提取[J]. 電子與信息學(xué)報(bào)，2006，28(4)： 643-646.

CHEN Hang-yong, LI Xiang, GUO Gui-rong, et al. Radar Feature Extraction of Micro-precession Ballistic Missile Warhead[J]. Journal of Electronics & Information Technology, 2006, 28(4): 643-646.

[7] 關(guān)永勝，左群聲，劉宏偉,等. 空間進(jìn)動(dòng)目標(biāo)微動(dòng)參數(shù)估計(jì)方法[J]. 電子與信息學(xué)報(bào)，2011，33(10)：2427-2432.

GUAN Yong-sheng, ZUO Qun-sheng, LIU Hong-wei, et al. Micro-motion Parameters Estimation of Space Precession Targets[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2427-2432.

[8] 賀三思，周建雄，付強(qiáng)，利用一維距離像序列估計(jì)彈道中段目標(biāo)進(jìn)動(dòng)參數(shù)[J]. 信號(hào)處理，2008，25(6): 925-929.

HE San-si, ZHOU Jian-xiong, FU Qiang. Using HRRP Sequence to Estimate the Precession Parameters of Midcourse Target[J]. Signal Processing, 2008, 25(6): 925-929.

[9] 高紅衛(wèi)，謝良貴，文樹梁，等. 彈道導(dǎo)彈目標(biāo)微多普勒特征提取[J].雷達(dá)科學(xué)與技術(shù)，2008，6(2)，96-101.

GAO Hong-wei, XIE Liang-gui, WEN Shu-liang, et al. Micro-Doppler Feature Extraction of Ballistic Missile Targets[J]. Radar Science and Technology, 2008, 6(2), 96-101.

[10] 黃培康，殷紅成，許小劍. 雷達(dá)目標(biāo)特性[M]. 北京：電子工業(yè)出版社，2005.

HUANG Pei-kang, YIN Hong-cheng, XU Xiao-jian. Radar Target Characteristic[M]. Beijing：Publishing House of Electronics Industry，2005.

[11] 彭拯.全局優(yōu)化的水平值逼近理論與算法研究[D].上海：上海大學(xué)，2009.

PENG Zheng. A Study on Theory and Algorithms of Level-Value Approximation to Global Optimization[D].Shanghai: Shanghai University, 2009.

[12] 袁莉，陶巍. 彈道導(dǎo)彈目標(biāo)的距離像特性與特征分析[J]. 制導(dǎo)與引信，2009，30(2)：7-11.

YUAN Li, TAO Wei. Characteristics and Feature Analysis of Range Profile for Ballistic Missile Target[J]. Guidance & Fuze, 2009, 30(2): 7-11.

[13] 溫曉楊，盧大威，張軍. 快時(shí)間域微振動(dòng)對(duì)高分辨距離像畸變分析[J]. 現(xiàn)代防御技術(shù)，2010，38(6)：126-131.

WEN Xiao-yang, LU Da-wei, ZHANG Jun. HRRP Distortion Analysis of Vibration Scatters in Fast Time Domain[J]. Modern Defence Technology, 2010, 38(6), 126-131.

[14] 徐慶，王秀春，李青. 基于高分辨一維像的目標(biāo)特征提取方法[J]. 現(xiàn)代雷達(dá)，2009，31(6)：60-63.

XU Qing, WANG Xiu-chun, LI Qing. Extraction of Target Feature Using High Resolution Range Profile[J]. Modern Radar, 2009, 31(6): 60-63.