基于先驗知識的最優化傳感器部署方法*

劉忠義，張華睿，王妮，劉潔

(海軍潛艇學院，山東 青島 266042)

0 引言

目標檢測是防空作戰的關鍵環節。提高檢測概率對提高防空攔截效率、保護己方目標等具有十分重要的意義。然而，由于低空突防戰術和隱身技術的發展，防守方對攻擊目標的檢測正面臨巨大挑戰。因此，在現有傳感器資源條件下，通過優化傳感器部署方案，使得己方被保護目標達到最佳防護狀態成為一種現實而有效的途徑，開展這方面的研究也因此具有顯著的實用價值。

針對傳感器的最優化部署問題，現有的研究工作主要分為2部分，一是傳感器威力范圍對監測責任區的覆蓋最優化問題[1-4]，預先設定傳感器在各種場景下的威力范圍，然后通過優化部署方法使得多部傳感器對監測責任區的覆蓋比例達到最優；二是傳感器對監測目標的定位精度最優化問題[5-10]，通常目標的定位精度與傳感器的運動軌跡或者傳感器—目標的幾何位置關系有關，合理規劃傳感器部署位置可有效提高目標定位精度。以上2部分均從不同角度對傳感器最優化部署問題進行了研究，但是對于突防目標的檢測卻缺乏深入分析。

本文以航母編隊防空作戰為背景，從目標檢測的角度對預警機的最優化部署問題進行了探討。由于預警機能克服地球曲率的影響，探測范圍大大優于水面艦船搭載的雷達，因此其主要擔任航母編隊防空警戒任務，用于檢測早期突防目標[11]。在進行預警機部署時，一些先驗知識和戰術規則也可以作為決策依據引入到優化算法中，如突防目標的攻擊意圖、可能出現的攻擊方位等等。本文對突防目標的作戰意圖進行分析，建立了目標來襲方位的模型，然后結合預警機探測性能，推導得到預警機對目標的綜合檢測概率，最后給出了一種以檢測概率為優化函數的最優部署方法。

1 問題描述

在一個由多艘艦船組成的航母編隊中，航母作為艦載機搭載平臺，其擁有其他水面艦船無可比擬的重要性。航母編隊若損失航母，將失去絕大部分戰斗力。因此在部署預警機位置時，首要考慮因素為航母的保護[12]。航母編隊的防御范圍為以航母為中心、半徑為R的一個圓，如圖1所示。角度θ表示突防目標T進入防御圈的位置，其中正北方向為0°方位角，順時針方向為正。根據先驗知識，可預先獲取突防目標在各個方位出現的概率。若艦隊中部署N個預警機，其性能分別表示為：在一定虛警Pf下，預警雷達對參照目標的檢測概率達到P0時，目標與雷達的距離為ri0,i=1,2，…,N。由于預警機承擔的主要探測任務為突防目標的早期檢測，本文將以對目標的檢測概率為預警機部署方案的度量函數，即綜合檢測概率越高，部署方案越優，同時為了預警機的自身安全，限定其與航母的徑向距離應小于預定值rmax。最終本文問題可描述為：在已知預警機探測性能的情況下，如何部署其位置S(xi,yi),i=1,2，…,N，使得其與航母的徑向距離小于rmax時，對穿越防御圈的突防目標的綜合檢測效率達到最優。

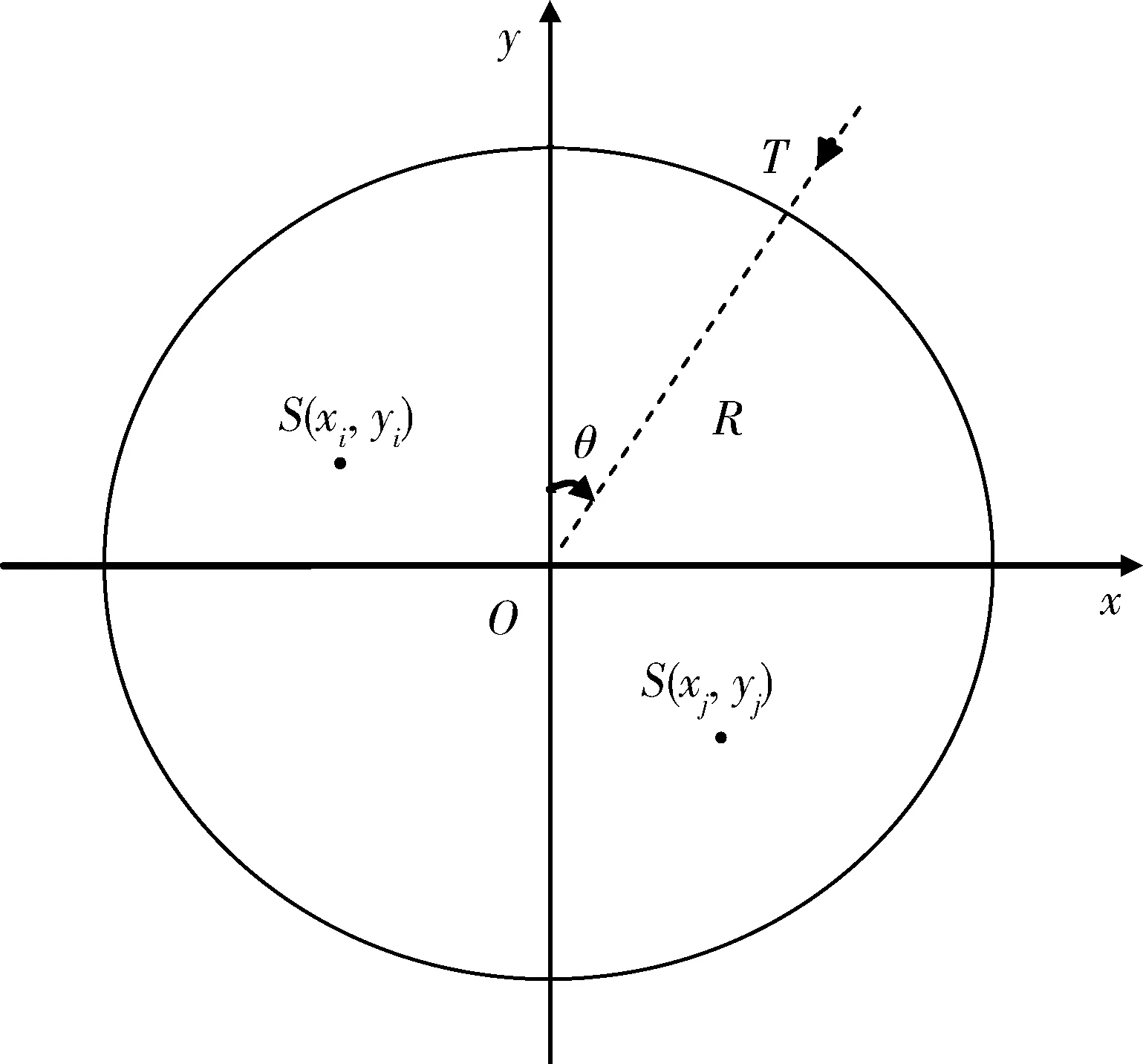
圖1 航母編隊防空示意圖Fig.1 Illustration of aircraft carrier formation in antiair battle

2 預警機優化部署模型

依據首要保護目標為航母的原則，以預警機對目標的綜合檢測概率為優化函數，逐步建立預警機的優化部署模型。本文將從預警機對目標的檢測能力和目標的可能突防角度這2個方面分別展開討論。

2.1 預警機對目標檢測概率

首先考慮單個預警機部署在任意陣位(x,y)時，對進入防御圈的突防目標的檢測概率。預警機的性能描述為：當虛警為Pf時，對距離為r0的參照目標的檢測概率為P0。假定針對SwerlingⅠ型目標，則檢測概率和信噪比滿足關系式[13]

(1)

由式(1)和預警機性能可得，目標在r0處的信噪比SNR0為

(2)

同時，目標的信噪比與距離的4次方成反比，則對于距離為r的目標，其信噪比可表示為

(3)

將式(3)代入式(1)，得到預警機對距離為r的目標檢測概率為

(4)

其中突防目標穿越防御圈時，其與預警機的距離r可通過預警機部署位置(x,y)和目標突襲方位θ得到

(5)

基于以上推導，當同時部署N個預警機，且位置分別為xi,yi,i=1,2,…,N時，對從方位θ突防的目標的聯合檢測概率為

(6)

式中：PDθ,xi,yi與ri可分別由式(4)、(5)得到。

(7)

2.2 目標出現方位先驗知識模型

若對敵方目標來襲方位無任何先驗信息的情況下，目標可能出現方位的概率在360°上均勻分布。此時，預警機需貼近航母部署，防止目標從各個角度突防。但是，根據敵方機場相對航母編隊方位、衛星圖像與上級敵情通報等等，指揮官對敵方目標可能來襲方位能有大致了解。如圖2a)所示。假設根據先驗知識，已知在我方編隊θ1和θ2方位角上，存在敵方機場或航母編隊，將其分別標定為威脅1和威脅2。則突防目標可能出現方位為敵方機場和航母的對應方位，并且以θ1和θ2為出現概率值的極大值點，偏離θ1和θ2出現概率值降低。以標準正態分布為基礎對目標來襲方位概率進行建模，則目標來襲方位概率密度函數為

(8)

式中：C為歸一化常數；θi為第i號威脅的中心方位，Ci為其相應的權重；σi表征目標來襲方位先驗知識。

當敵情不明時，目標可能出現方位不明確，σi應適當調大。若我方對敵方可能來襲方位具有較明確的先驗知識，σi應適當調小。指揮官可根據實時戰場態勢，動態調節σi大小。Ci則根據敵方機場的遠近、裝備飛機的數量和先進程度確定。圖2b)為目標來襲方位概率密度函數示意圖。其中威脅2相對于威脅1距離我方編隊更近，威脅程度更高，并且目標攻擊方位更明確，所以表現為其權重C2較大，攻擊方位偏差σ2較小。最終，確定各個參數分別為C1=0.6，C2=0.7，σ1=0.3°，σ2=0.2°，θ1=-20°，θ2=30°。

按照這種方法對先驗知識進行建模，當敵情不明確時，仍能提取到部分有用信息，而且當情報不準確時，因為該方法采用的是概率模型，可有效避免硬性判決所帶來的影響。

2.3 綜合檢測概率

經過上述分析，得到突防目標在各個方位出現的先驗概率和預警機對其的檢測概率，則由貝葉斯公式推導，當N個預警機采取某種部署方案時，其檢測到穿越防御圈的突防目標的全概率為

(9)

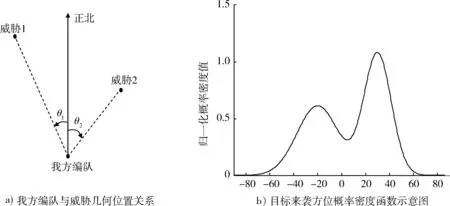
圖2 目標出現方位概率Fig.2 Probability of targets’ appearance angle

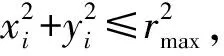
(10)

優化式(10)結合了具體的戰術需求，反映了預警機在航母編隊防空作戰中承擔的任務，并且其優化目的貼近實際應用過程。相對于以往的傳感器優化部署方法，本文所提出的優化函數具有更高的應用價值。

3 基于粒子群優化的近似算法

由于預警機部署陣位優化函數非線性化程度較高，且含有積分運算，難以得到解析結果，本文將利用粒子群優化算法來解決這個問題。

粒子群優化是一種高效的近似優化算法，由Kennedy和Eberhart在1995年提出[14]。其通過模擬生物界鳥群覓食的行為特性，來搜索全局最優解。由于鳥類具有記憶能力，每一只鳥或稱為粒子都會記下其運動軌跡中的最佳覓食位置(適應度函數值)，定義為局部最優值p；同時，整個種群所找到的最佳位置定義為全局最優值g，該值以廣播的形式告知種群中的每個粒子。粒子依據p和g調整當前的位置和飛行方向，其速度矢量分為3部分：往全局最優位置運動、往局部最優位置運動和保持原有速度，則粒子的位置更新方程為

(11)

式中：c1，c2為Hooke常數，也稱為認知因子和社會因子；x，v為粒子的位置和速度矢量；下標s表示迭代次數；η1，η2為服從均勻分布u(0,1)的隨機數；w為慣性加權因子。

為加快收斂速度，w通常取時變形式[15]

w=wmax-wminsmax-s/smax+wmin，

(12)

式中：wmax，wmin分別為慣性加權因子的最大值和最小值，取經驗值wmax= 0.9，wmin= 0.4；smax為最大允許迭代次數。

為避免粒子收斂到局部最優解，認知加速因子c1和社會加速因子c2同樣取時變形式[16]

(13)

式中：c1max，c1min，c2max，c2min分別為認知加速因子和社會加速因子的最大值和最小值，分別取經驗值c1max=c2max= 2.5，c1min=c2min= 0.5。

為防止粒子跳出搜索空間[17]，應根據搜索空間大小，設定最大速度限制vmax，則有||vs|| ≤vmax。

結合本文內容，以預警機的部署位置為優化變量，對突防目標的檢測概率作為適應度函數，則粒子群優化算法的步驟歸納如下：

步驟1：在搜索空間內隨機產生M個初始粒子位置，即預警機可能部署位置。

步驟2：判斷預警機部署位置是否滿足最大徑向距離約束，若不是，其適應度函數設置為0；若是，計算預警機部署在該位置時對突防目標的檢測概率，并將其賦予為對應的適應度函數值。

步驟3：根據各個粒子的適應度函數值更新p和g。

步驟4：依據式(11)～(13)更新粒子速度矢量和位置矢量。

步驟5：判斷是否達到最大迭代次數，若滿足則執行步驟6，否則執行步驟2。

步驟6：選取全局最優值對應的位置作為預警機部署的優化解，算法結束。

4 仿真實驗

本文設計了2個仿真實驗對文中方法的有效性進行檢驗。

實驗1：單威脅，單預警機場景

假設航母防御圈半徑為600 km，艦隊部署1架預警機，其性能可表述為對距離為500 km的某型轟炸機檢測概率為0.8，虛警為10-5。預警機與航母最大徑向距為450 km。粒子群優化算法中，產生粒子數為10 000，粒子在每個運算周期的最大飛行距離為100 m，迭代200次，搜索空域設定為x軸(-600，600) km和y軸(-600，600) km的范圍。圖3給出了先驗知識σ與綜合檢測概率P的關系圖。

圖3 先驗知識σ與綜合檢測概率P變化關系Fig.3 Relationship of the priori information and detection probability

從圖3可以看出，若對目標可能來襲方位有較豐富的先驗知識，對應于σ較小，則對目標的檢測概率會較高；概率值隨著先驗知識的減少而降低，以至于趨近最小極限值0.636。而按照傳統方法，由于不利用對突防目標的先驗知識，只能將預警機貼近航母部署，其檢測概率一直維持在0.636的最低值。

實驗2：雙威脅，雙預警機場景

假設航母防御圈半徑為600 km，艦隊部署2架預警機，其性能均可表述為對距離為300 km的某型轟炸機檢測概率為0.8，虛警為10-5。預警機與航母最大徑向距為450 km。粒子群優化算法參數設定如實驗1。戰場存在2個威脅，其模型參數如圖 2所示。利用本文方法計算得到預警機最優部署位置為(-172.68, 398.76) km，(226.28, 388.92) km，檢測概率為0.968 5。在傳統方法中，一般將預警機貼近航母部署或者沿威脅軸方向上前出。按照此思路部署預警機位置為(0, 0) km，(0, 450) km，其檢測概率只有0.789。可以看出，本文提出的預警機部署方法，有效地提高了對突防目標的檢測概率。

若設定預警機對轟炸機的檢測概率達到0.8時，以此時轟炸機與預警機的距離作為預警機的實際探測距離。當其他參數不變時，圖4給出了預警機實際探測距離與綜合檢測概率關系圖。其中實線為本文方法，虛線為傳統方法。可以看出，利用本文的優化部署方法，對突入航母防御圈的目標檢測概率獲得較大提高。這是通過將預警機的探測能力從目標不太可能出現的方位轉移到重點防護方位上，使得對目標的綜合檢測效率達到了最優。

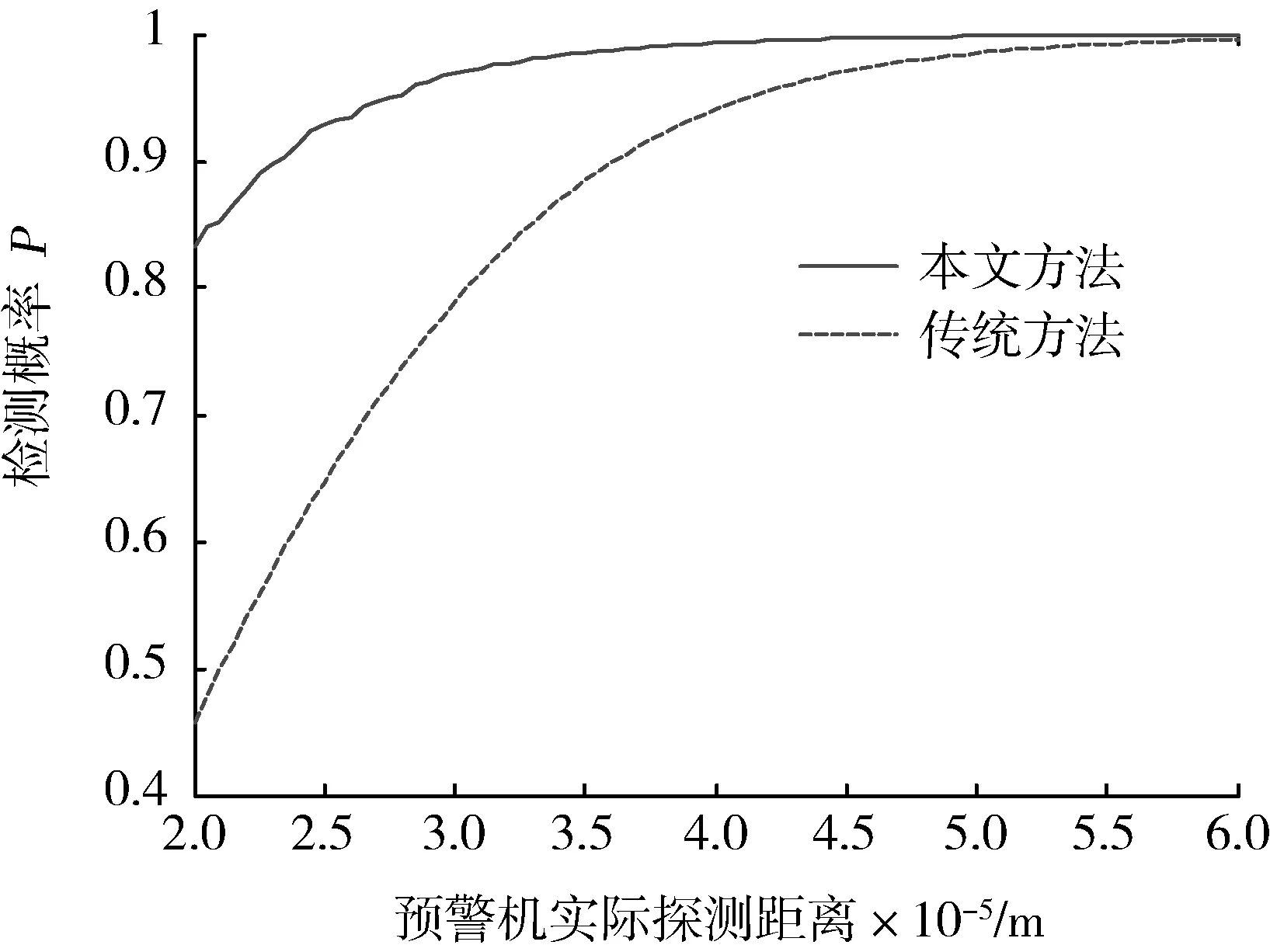
圖4 預警機實際探測距離與綜合檢測概率關系圖Fig.4 Relationship of real detection range and detection probability

通過這2組實驗表明，將目標的先驗知識引入到預警機優化部署問題，使得預警機對目標的檢測概率大幅提高，并且先驗知識越豐富，檢測概率越高。仿真結果符合預期設想。

5 結束語

本文以航母編隊中預警機對突入防御圈的敵方目標的檢測概率作為優化函數，討論了預警機的最優部署問題。通過對目標可能出現的方位建模，在優化算法中引入已獲取的突防目標的先驗知識。仿真實驗表明，目標的先驗知識使得預警機對目標的檢測概率有較大的提高。

參考文獻：

[1] 王中杰, 李俠, 周啟明, 等. 基于多約束條件遺傳算法的雷達網優化部署[J]. 系統工程與電子技術, 2008, 30(2):265-268.

WANG Zhong-jie, LI Xia, ZHOU Qi-ming, et al. Optimal Deployment of Radar Network Based on Multi-Constrained GA[J]. Systems Engineering and Electronics, 2008, 30(2):265-268.

[2] OSMANI A, HAGHIGHT A, DEHGHAN M, et al. FSPNS: Fuzzy Sensor Placement Based on Neighbors State [C]∥Proc. of the 12th International Conference on Computer Modelling and Simulation, 2010:549-552.

[3] YI Yao, CHEN Chuang-hao, ABIDI B, et al. Can You Sen Me Now? Sensor Positioning for Automated and Persistent Surveilance[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2010, 40(1):101-115.

[4] AKHLAGHINIA R, HASHEMI S, SHADGAR B. Sensor Placement for Heterogeneous Point Coverage[C] ∥Proc. of the Second International Conference on Computer and Network Technology, 2010:13-17.

[5] YANG C, KAPLAN L, BLASCH E, et al. Optimal Placement of Heterogeneous Sensors in Target Tracking[C]∥Proc. of the 14th International Conference on Information Fusion，2011:1-8.

[6] ARANDA S, MARTINEZ S, BULLO F. On Optimal Sensor Placement and Motion Coordination for Target Tracking[R]. Santa Barbara, CA: Department of Electrical and Computer Engineering, University of California, 2004:1-9.

[7] RAJAGOPLAN R, NIU R, MOHAN C, et al. Sensor Placement for Ballistic Missile Localization Using Evolutionary Algorithms[C]∥Proc. of the IEEE International Conference on System, Man and Cybernetics，2007:284-289.

[8] CHANG Xiang-mao, TAN Rui, XING Guo-liang, et al. Sensor Placement Algorithms for Fusion-Based Surveillance Networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(8):1407-1414.

[9] BISHOP A, FIDAN B, ANDERSON B, et al. Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 1-Bearing-Only Localization[C]∥Proc. of the Third International Conference on Intelligent Sensor, Sensor Networks and Information，2007:13-18.

[10] BISHOP A, FIDAN B, ANDERSON B, et al. Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 2-Time-of-Arrival Based Localization[C]∥Proc. of the Third International Conference on Intelligent Sensor, Sensor Networks and Information, 2007:7-12.

[11] 曹毅, 苗德成, 路建偉, 等. 聯合防空偵察預警系統探測能力淺析[J]. 系統工程與電子技術, 2006, 28(2):253-256.

CAO Yi, MIAO De-cheng, LU Jian-wei, et al. Analysis on Detecting Ability of the Early-Warning System for Joint Air-Defense[J]. Systems Engineering and Electronics, 2006, 28(2):253-256.

[12] 張蕾, 鄧大松. 航母編隊預警探測技術文集：美國海軍航母編隊與作戰使用[R]. 南京: 中國電子科技集團公司第十四研究所, 2008:13-22.

ZHANG Lei, DENG Da-song. Collected Papers on Carrier Strike Group EW Detection Techniques: U.S. Navy Carrier Battle Group and Engagement Principle[R]. Nanjing: the 14th Research Institute of China Electronics Science Company, 2008:13-22.

[13] 盧建斌. 相控陣雷達資源優化管理的理論與方法[D]. 長沙: 國防科技大學, 2007.

LU Jian-bin. Theory and Method of Resource Optimization and Management for Phased Array Radars[D]. Changsha: National University of Defense Technology, 2007.

[14] KENNEDY J, EBERHART R. Particle Swarm Optimization [C]∥Proc. of the IEEE Conference on Neural Networks, 1995:1942-1948.

[15] SHI Y, EBERHART R. Parameter Selection in Particle Swarm Optimization[C]∥Proc. of the International Conference on Evolutionary Program, 1998:591-600.

[16] RATNAWEERA A, HALGAMUGE S K, WATSON H C. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):240-255.

[17] KENNEDY J. The Particle Swarm: Social Adaptation of Knowledge[C] ∥Proc. of the IEEE International Conference on Evolutionary Computation, 1997:303-308.