Monin-Obukhov理論在蒸發波導PJ模式中的應用*
李梁,張海勇,闞榮才
(海軍大連艦艇學院 通信系,遼寧 大連 116018)
0 引言
無線電通信技術的應用,改變了傳統的通信方式,海上通信保障能力得到了質的提高。近年來,有關無線電傳播理論和應用的研究得到了空前發展。在無線電通信和探測過程中偶然出現的超視距傳播、探測空洞等問題促進了對對流層大氣波導的發現和研究。大氣波導的出現,可以使其中的電磁波以較少的損耗沿波導傳播,可以對通信系統和探測系統的運作產生嚴重影響,它既可以實現遠距離傳輸同時也會導致雜波增強干擾加大。所以深入研究大氣波導傳播機理及探測方法具有重大理論意義和實際軍事價值。
無線電通信是海上通信的主要手段,受海上蒸發波導影響較大,電波的反常傳播大多數是由蒸發波導現象引起的[1]。目前,針對蒸發波導環境的預測模式主要有2種,即PJ(paulus Jeske)模式和MGB(Musson-Genon-Gauthier-bruth)模式[2]。本文主要對基于Monin-Obukhov相似理論的蒸導PJ模式進行了分析。
1 蒸發波導高度探測理論
1.1 蒸發波導的形成條件
大氣波導主要有3類:表面波導(又稱基面波導)、懸空波導(又稱抬升波導)、蒸發波導。其中蒸發波導出現在海洋環境中。
蒸發波導是因海面蒸發使濕度在很小的垂直高度范圍內發生銳減而形成的一類特殊的表面波導。緊貼海面的氣層,因海水的蒸發可以達到飽和狀態,而在其以上高度的空氣通常達不到飽和狀態,導致濕度在很小的垂直高度范圍內發生銳減,使得大氣修正折射指數自海面向上迅速遞減,當到達一定高度后,大氣修正折射指數達到最小,該高度稱為蒸發波導高度(或蒸發波導厚度),見圖1[3]。蒸發波導高度通常在6~30 m。盡管在世界幾乎所有海域任何時候都可能存在著蒸發波導,但其高度隨地理緯度、季節、一日之內不同時間而變化,一般是在低緯度海域、夏季、白天蒸發波導高度較高,在高緯度海域冬季夜間蒸發波導高度可能只有1~2 m;而在赤道緯度附近夏季晝間,蒸發波導可能達到40 m高度;在世界海域范圍內,蒸發波導高度約13 m[4]。蒸發波導高度是一個與波導強度有關的量,它反映波導捕獲電磁波的能力。
海面微氣象條件對蒸發波導產生嚴重的影響,所以,對于蒸發波導高度的確定,目前只能根據近地層相似理論利用海面氣象和海洋觀測資料來確定[5]。
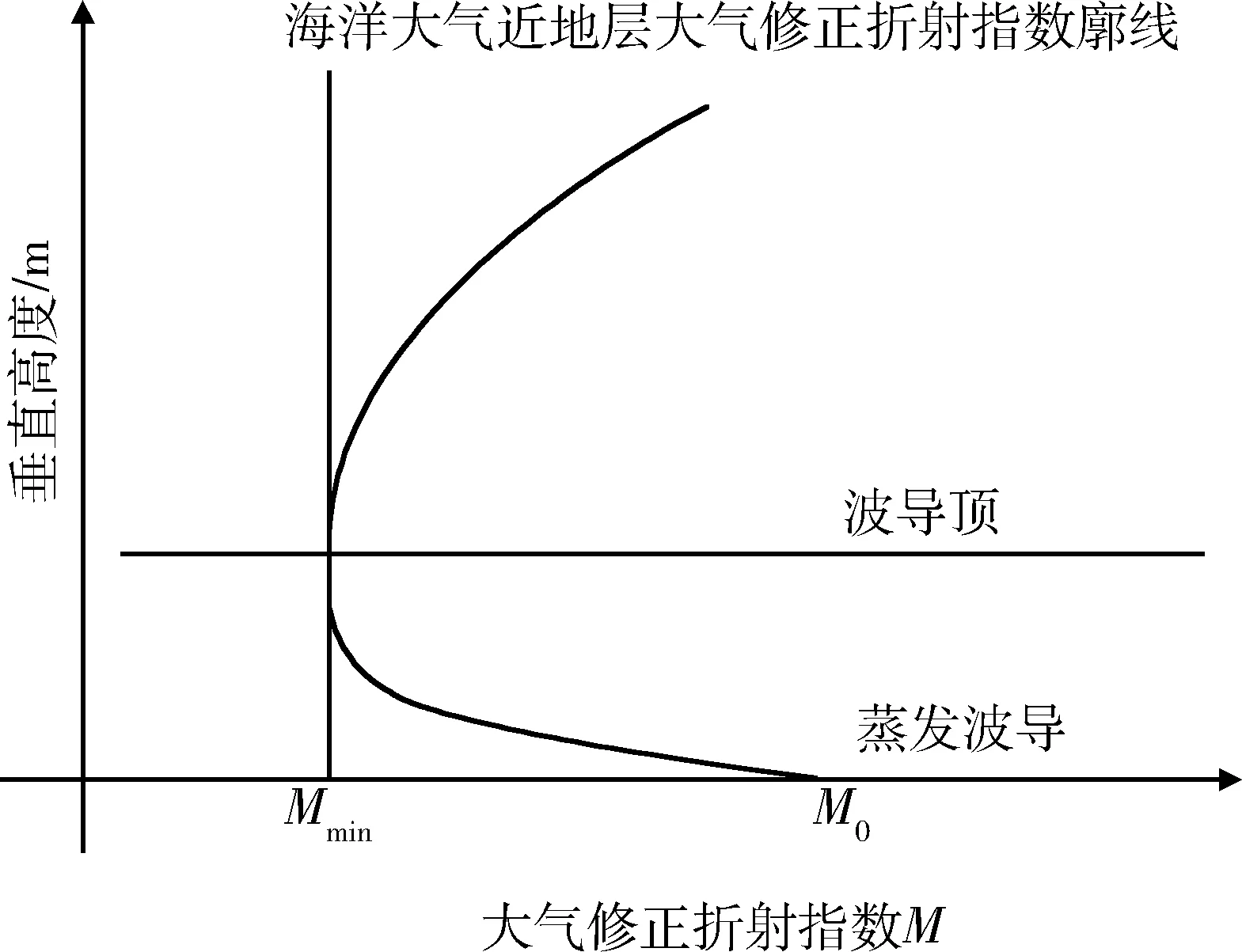
圖1 蒸發波導Fig.1 Evaporation duct
1.2 蒸發波導高度預測原理
蒸發波導出現在海洋大氣近地層內,其形成受海氣界面處微氣象條件影響,目前難以通過利用諸如無線電探空儀、低空火箭探空儀或微波折射儀等探測或遙感手段直接確定。
根據近地層相似理論利用海面宏觀氣象水文觀測來確定蒸發波導高度的模式有多種,包括PJ模式、MGB模式、S.M.Babin模式、LKB模式等。這些模式的基本原理都是依賴近地層相似理論,不同的只是用于確定近地層通量和特征尺度的方法。其中,PJ模式和MGB模式較為常用。
2 Monin-Obukhov相似理論
蒸發波導受海氣交界面處微氣象條件影響與制約,使得直接測量海洋大氣近地層內大氣折射指數輪廓線十分困難。目前,通常利用莫寧-奧布霍夫(Monin-Obukhov)相似理論來確定蒸發波導高度和海洋大氣近地層大氣折射指數輪廓線。如果要對蒸發波導進行預報,則還需要利用整體邊界層相似理論獲得邊界層外參數進而確定近地層特征尺度。
2.1 Monin-Obukhov 相似關系式
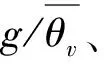
式中:ρ為空氣密度;cpa為空氣定壓比熱。
利用Buckingham的π定理對以上各式進行量綱分析,確定函數Fu,Fh,Fq的形式分別如下:
(1)
(2)
(3)
式中:u*為速度特征尺度,稱為摩擦速度;θ*為溫度特征尺度;q*為水汽特征尺度;L為長度特征尺度;k為Karman常數,取k=0.4;L稱為Monin-Obukhov長度(以下稱為M-O長度)。
無量綱參數ζ=h/L其物理意義表示湍能的浮力產生與湍能的切變耗散之比,稱為層結構穩定度參數。ζ>0時,層結是穩定的;ζ<0時,層結是不穩定的;ζ=0時,層結是中性的。Φu,Φt,Φq為穩定度參數ζ的函數,稱為普適函數,這些普適函數一般需要根據實測資料來確定,不同研究人員利用不同實測資料給出的普適函數略有不同,在中性層結條件下Φu,Φt,Φq均等于1。式(1)~(3)稱為M-O相似關系式。
2.2 總體查理孫數的引入
無量綱參數ζ雖然被稱作穩定性參數,但其量值無論與靜力還是動力的穩定性都沒有直接關系,而理查孫數Ri是一個直接靜力和動力穩定性聯系在一起用來描述穩定度的參數。通量理查孫數Rif定義為
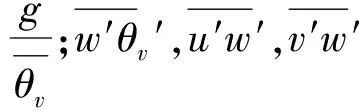
在實際應用中,對于梯度理查孫數中的微分通常用差分代替,得到新的理查孫數稱為總體理查孫數Rib:
由于總體理查孫數Rib可以較方便地利用平均風、溫度輪廓線資料求取,因此,通常尋找理查孫數Ri與穩定度參數ζ=h/L的關系,再由Ri確定h/L。若忽略濕度影響,在近地層中,梯度理查孫數Ri可由下式定義
式中:u為水平風速;2為海面以上垂直高度;T為氣溫。
2.3 海洋大氣近地層相似理論的應用
在海洋大氣層的近地層中,許多實際問題需要借助于Monin-Obukhov相似理論加以解決。
由Monin-Obukhov相似關系式(1)~(3)得
(4)
(5)
(6)
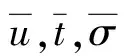
在實際應用中,通常使用梯度形式的Monin-Obukhov長度L′代替L,若忽略濕度的影響,在近地層中,梯度Monin-Obukhov長度L′可由下式定義:
(7)
而各物理量垂直分布輪廓線的普適函數Φu,Φt,Φσ取相同值,記為Φ。對穩定層結,Jeske建議使用Monin-Obukhov提出的對數線性關系:
(8)
對于不穩定層結Jeske建議使用KEYPS關系[5-6]:
(9)
將式(4)~(6)兩邊分別從海面粗糙高度h0積分到參考高度h1,得
(10)
(11)
(12)
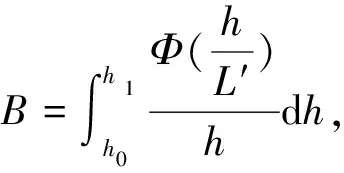
為了便于計算通常利用梯度理查孫數Ri與h/L之間的關系,通過Ri來確定h/L。近地層中,Ri可以由下式求得
(13)
分別將(7)式及式(10)~(12)代入式(4)~(6)中得到:
(14)
(15)
(16)
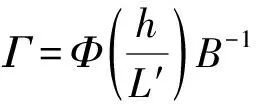
將式(13),(14)代入式(12)中得到總體理查孫數:
(17)
顯然,Γ是Rib的函數。函數Γ依據不同的Rib值選用不同的計算方式[6]:
Γ=0.05,Rib≤-3.75,
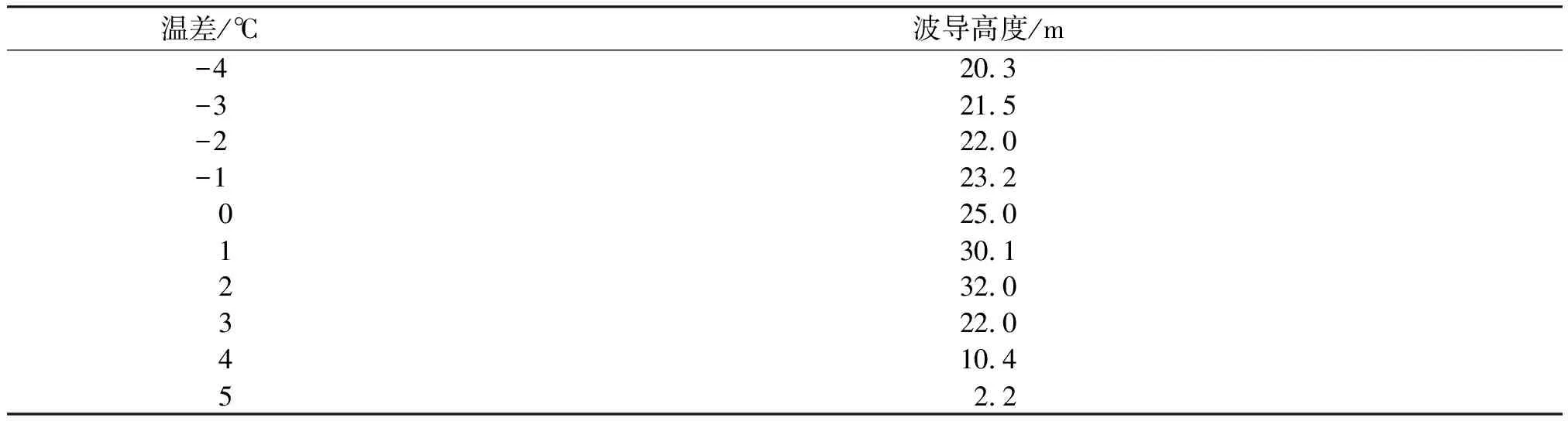
Γ=0.065+0.004Rib, -3.75 Γ=0.109+0.367Rib, -0.12 Γ=0.155+0.021Rib, 0.14 由式(14),(15)及(11)可將式(7)變為 (18) 根據式(17),L′可以表示為 (19) 這樣就可以通過Rib來確定L′。確定L′后,普適函數Φ和積分B就可以確定,最后可以根據式(13)確定物理屬性量σ的垂直分布輪廓線。 PJ模式是出現較早并被廣泛應用于蒸發波導預測的一種模式,其利用6 m作為參考高度測得氣溫、相對濕度、海表溫度以及風速作為輸入量,取海表面大氣壓為常數1 000 hPa,運用Monin-Obukhov相似理論,根據波導的偽折射率臨界梯度求得蒸發波導高度。 若取物理屬性量σ為偽折射指數Np,則式(14)變為 (20) ΔNp=Nph1-Nph0, (21) 式中:Nph1,Nph0分別為參考高度和海綿粗糙度高度處的偽折射指數。 當偽折射指數初值梯度等于臨界梯度b時,所對應的高度就是蒸發波導高度d,由式(20)可得 (22) 在穩定或中性層結中,由式(8)及B= (23) 將式(8)代入式(22),整理后得 (24) 式(24)就是穩定層或中性層結條件下蒸發波導高度d的計算式。 對于不穩定層結,由式(9)和式(22)可得不穩定層結條件下蒸發波導高度的計算式: (25) 式中:B由下式確定: (26) (27) 當然PJ模式也存在其局限性,文獻[7]指出:如果風速小于0.019 km/h,則將蒸發波導高度直接設為0,只有風速大于0.019 km/h,則該模式才適用,即:PJ模式沒有提供低風速條件下的Monin-Obukhov相似理論拓展方法[8-9]。 在相對濕度為75%,海面溫度為25 ℃,風速為10 m/s的條件下,利用以上方法分別計算穩定層結、中性層結、不穩定層結條件下的蒸發波導高度。此處取氣-海溫差在-4 ℃~5 ℃變化時的計算結果。當氣-海溫差大于0時為穩定層結;等于0時為中性層結;小于0時為不穩定層結[10]。計算結果如表1所示。 由計算結果可以看出,當相對濕度和風速一定時,在不穩定層結條件下,蒸發波導高度隨氣-海溫差代數值增大而緩慢升高;在穩定層結條件下,波導高度先是隨溫差代數值增大而迅速增大,后又隨溫差代數值的增大而迅速降低。蒸發波導高度隨溫差代數值增大而增高可能是因為溫差值的增大意味著大氣層結穩定度增強,溫度垂直梯度對折射指數垂直梯度的貢獻逐漸由與濕度垂直梯度的貢獻異號變為同號,更有助于蒸發波導的形成[11-12]。但在極端穩定條件下,湍流運動被抑制,蒸發波導高度反而降低。 表1 不同溫差下波導高度值 根據Monin-Obukhov相似理論在大氣邊界層理論的基礎上,運用PJ模式對蒸發波導的高度進行推算,有效解決了蒸發波導探測受海面微氣象條件影響和制約的問題。分析了蒸發波導高度在穩定層結、中性層結及不穩定層結3種典型條件下的變化規律。利用確定的波導高度選擇信號發射仰角,使其能夠被波導層所捕獲,實現超視距傳輸,增加通信系統的通信距離;在不需要的情況下可改變發射角度,避開波導層,克服其給電子系統帶來的額外雜波等負面影響,具有重要的軍事應用價值。 參考文獻: [1] ANDERSON K D.94-GHz Progagation in the Evaporation Duct[J].IEEE Trans.Antennas Propag,1990,38(5):746-753. [2] 劉成國.蒸發波導環境特性和傳播特性及其應用研究[D].西安:西安電子科技大學, 2003. LIU Cheng-guo.Research on Evaporation Duct Propagation and Its Applications[D].Xi’an:Xidian University,2003. [3] 姚展予,趙柏林,李萬彪,等.大氣波導特征分析及其對電磁波傳播的影響[J].氣象學報,2000,58(5):605-616. YAO Zhan-yu,ZHAO Bo-lin,LI Wan-biao,et al.The Analysis of Characteristics of Atmospheric Waveguide and its Influence on Electromagnetic Wave Propagation[J].Acta Meteorologica Sinica,2000,58(5):605-616. [4] Kamran Khan.Thesis,Refractive Condition in Arabian Sea and Their Effects on ESM and Airborne Radar Operation[D].Naval Postgraduate School,1990. [5] JESKE H.The State of Radar-Range Prediction Over Sea,in Troospheric Radio Wave Propagation[J].ParteⅡ,AGARD-CP-70,1971:55-77. [6] RICHARD A.Paulus,Specification for Evaporation Duct Height Calculations[J].Naval Ocean Systems Center,TD-1685,1989:165-169. [7] 王海華. 大氣波導環境中電波傳播特性及其應用研究[D].西安:西安電子科技大學,2006. WANG Hai-hua.Research on Tropospheric Duct Propagation and Its Applications[D].Xi’an:Xidian University,2006. [8] 張瑜,吳少華.大氣波導傳播類型及特性分析[J].電波科學學報,2009,24(1):185-190. ZHANG Yu,WU Shao-hua.Analysis of the Type and Characteristics of Atmospheric Duct Propagation[J].Chinese Journal of Radio Science,2009,24(1):185-190. [9] 郭濤,張潔寒,劉瑩,等.利用蒸發波導進行超視距探測的條件研究[J].河南師范大學學報,2011,39(4):181-184. GUO Tao,ZHANG Jie-Han,LIU Ying,et al.Survey the Conditions of Take Advantage of Evaporation Duct for Over-the-Horizon Detection[J].Journal of HenanUniversity,2011,39(4):181-184. [10] 胡曉華,費建芳,張翔,等.氣象條件對大氣波導的影響[J].氣象學報,2007,27(3):349-354. HU Xiao-hua,FEI Jian-fang,ZHANG Xiang,et al.The Effect of Meteorological Conditions on Atmospheric Duct[J].Scientia Meteorologica Sinica,2007,27(3):349-354. [11] 李云波,張永剛,唐海川,等.基于海氣通量算法的海上蒸發波導診斷模型[J].應用氣象學報,2009,20(5).:628-633 LI Yun-bo,ZHANG Yong-gang,TANG Hai-chuan,et al. Diagnosis Model of Maritime Evaporation Duct Based on the Air-Sea Flux Algorithm[J] .Journal of Applied Meteorological Science,2009,20(5):628-633. [12] 戴無懼.微波通信中大氣波導干擾的工程估算[J].通信技術,1996,93(2):44-48. DAI Wu-ju.Project Estimate of Atmospheric Waveguide Interference in Microwave Communication [J]. Communication Technology, 1996,93(2):44-48.3 paulus Jeske(PJ)模式確定蒸發波導高度
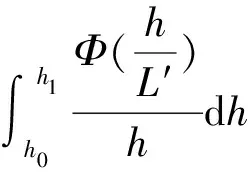
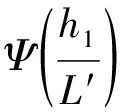
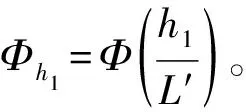
4 結束語

