瞄準(zhǔn)式戰(zhàn)斗部威力半徑與起爆延時(shí)研究*

石志彬，高敏，楊鎖昌，韓路杰

(石家莊機(jī)械工程學(xué)院 電子工程系，河北省 石家莊 050003)

0 引言

定向戰(zhàn)斗部是反戰(zhàn)術(shù)彈道導(dǎo)彈(tactical ballistic missiles, TBM)研究的熱點(diǎn)之一，瞄準(zhǔn)式戰(zhàn)斗部是定向戰(zhàn)斗部的一種，它可用于防空導(dǎo)彈攔截飛機(jī)、TBM等各種空中目標(biāo)。再入段反TBM一般采用逆軌攔截的方式，利用彈目之間高相對速度毀傷目標(biāo)[1-2]。瞄準(zhǔn)式戰(zhàn)斗部的破片位于柱形裝藥的前端面，裝藥、破片以及安執(zhí)系統(tǒng)共同固接在一個(gè)萬向轉(zhuǎn)臺上，轉(zhuǎn)臺可在一定范圍內(nèi)帶動戰(zhàn)斗部瞄準(zhǔn)不同位置。平時(shí)轉(zhuǎn)臺置于零位，即與導(dǎo)彈軸線重合，彈目交會階段，導(dǎo)引頭和引信可以探測到目標(biāo)的相對速度及位置信息，彈上計(jì)算機(jī)控制萬向轉(zhuǎn)臺瞄準(zhǔn)相對速度方向，并利用慣導(dǎo)信息去耦，保持戰(zhàn)斗部指向相對大地不變。彈上計(jì)算機(jī)還可利用探測信息計(jì)算出引信最佳起爆延時(shí)，在預(yù)定時(shí)刻起爆戰(zhàn)斗部。戰(zhàn)斗部爆炸后，驅(qū)動破片沿瞄準(zhǔn)方向以一定錐角軸向飛散，攔截目標(biāo)并將其毀傷。

從作用原理可以看出瞄準(zhǔn)式戰(zhàn)斗部的破片飛散與傳統(tǒng)周向均勻戰(zhàn)斗部有很大區(qū)別，引戰(zhàn)配合和最佳起爆延時(shí)等問題有其特殊性，需要對其進(jìn)行系統(tǒng)研究。從公開的文獻(xiàn)來看，美國的Lloyd博士[3-4]對瞄準(zhǔn)式戰(zhàn)斗部的作用原理、引戰(zhàn)配合以及彈上應(yīng)用等方面問題進(jìn)行了探討，莊志洪教授對該類型戰(zhàn)斗部引戰(zhàn)能力做過分析，得出了一些有價(jià)值的結(jié)論[5]，國內(nèi)還有一些專著提到過機(jī)械轉(zhuǎn)向式戰(zhàn)斗部[6]等，但他們都沒有更進(jìn)一步地給出最佳起爆延時(shí)的求解方法。美國海軍AD報(bào)告針對空空導(dǎo)彈提出一種延時(shí)模型[7-8]，它采用計(jì)算目標(biāo)剩余飛行時(shí)間和戰(zhàn)斗部破片飛行時(shí)間的方法得到最佳起爆延時(shí)。但是該模型適用于破片飛散前傾角固定的戰(zhàn)斗部，并沒有考慮到破片前傾角可變時(shí)的情況。

本文首先通過靜爆試驗(yàn)得到破片分布數(shù)據(jù)，并據(jù)此計(jì)算戰(zhàn)斗部的威力半徑；然后在瞄準(zhǔn)式戰(zhàn)斗部最佳毀傷距離結(jié)論的基礎(chǔ)上，利用導(dǎo)引頭失效前某一時(shí)刻所測參數(shù)和引信探測到目標(biāo)初始時(shí)刻所測參數(shù)，推導(dǎo)出引信起爆的最佳延時(shí)，并定量分析其主要影響因素。

1 靜爆試驗(yàn)及戰(zhàn)斗部威力半徑

1.1 前向戰(zhàn)斗部靜爆試驗(yàn)

靜爆試驗(yàn)?zāi)康氖堑玫届o態(tài)條件下破片的空間分布情況(分布均勻性與飛散角)，為確定戰(zhàn)斗部靜態(tài)威力半徑提供數(shù)據(jù)。

試驗(yàn)場地設(shè)置參考相關(guān)國家軍用標(biāo)準(zhǔn)[9-10]，如圖1所示。戰(zhàn)斗部水平臥放于托彈架上，與靶板中心同高，其軸延長線穿過兩靶板接縫的中點(diǎn)。采用2塊鋼質(zhì)靶板攔截破片，其尺寸均為1.5 m×1.5 m，每塊靶板與戰(zhàn)斗部爆心的距離為5 m，且與地面垂直，靶后布設(shè)高速攝影儀。

圖1 戰(zhàn)斗部與靶板的位置關(guān)系Fig.1 Position of target plates and warhead

戰(zhàn)斗部采用高密度鎢合金材料的立方體預(yù)制破片，單枚破片質(zhì)量25 g，數(shù)量N=261枚，均勻緊密排列在戰(zhàn)斗部前端，起爆點(diǎn)位于戰(zhàn)斗部底端中心。

厚6 mm的鋼靶板在5 m的距離上可被25 g鎢破片輕易穿透，試驗(yàn)后的穿孔情況如圖2所示。破片場中間密度大，外圍密度小，破片散布中心位于兩靶板接縫中點(diǎn)附近。破片分布數(shù)據(jù)經(jīng)處理后有以下結(jié)論：①著靶破片數(shù)為196枚，合理估計(jì)上下側(cè)逸出的破片，在以瞄準(zhǔn)點(diǎn)為中心的3 m×3 m范圍內(nèi)總計(jì)著靶215枚；②考慮場密度要求，按著靶破片80%統(tǒng)計(jì)，所在圓直徑為1.32 m，破片束靜態(tài)錐角為θs=15.04°；③中間破片平均速度為1 612 m/s，邊緣破片平均速度為1 508 m/s。

圖2 試驗(yàn)后鋼靶板的穿孔情況Fig.2 Penetration holes in the target plate

1.2 瞄準(zhǔn)式戰(zhàn)斗部靜態(tài)威力范圍

配用于防空導(dǎo)彈時(shí)，戰(zhàn)斗部艙前段是導(dǎo)引頭，如果戰(zhàn)斗部轉(zhuǎn)角過小，導(dǎo)彈前部艙段會嚴(yán)重阻擋破片飛行，若戰(zhàn)斗部轉(zhuǎn)角過大，轉(zhuǎn)臺框架、驅(qū)動電機(jī)、彈上電纜、艙段蒙皮或加強(qiáng)筋等也會對破片造成嚴(yán)重遮擋。所以，為減少爆炸后破片前進(jìn)路徑上的遮擋，確定轉(zhuǎn)臺的轉(zhuǎn)角范圍為20°<αs<80°。

王樹山[11-13]等通過“升-降”法試驗(yàn)，得出2.7 g的鎢合金破片在868.6 m/s的速度下，穿透4 mm鋼板(45#鋼)后可引爆注裝B炸藥，其破片撞擊動能為1 019 J。瞄準(zhǔn)式戰(zhàn)斗部單枚破片質(zhì)量為25 g，在動態(tài)條件下撞擊目標(biāo)速度可達(dá)4 000 m/s，破片撞擊動能高達(dá)2.0×105J，約為文獻(xiàn)[11]中臨界值的200倍。目前對于破片引爆TBM彈頭條件還沒有統(tǒng)一判據(jù)，本文參考文獻(xiàn)[11]中的結(jié)論，認(rèn)為瞄準(zhǔn)式戰(zhàn)斗部單枚破片具備引爆目標(biāo)的能力。

因此，以1枚破片擊中目標(biāo)有效載荷為毀傷判據(jù)，令破片數(shù)N=200，TBM目標(biāo)有效載荷截面半徑rt=0.44 m，目標(biāo)軸切面面積Stq=0.9 m2，建立模型并計(jì)算出戰(zhàn)斗部靜態(tài)條件下的威力場范圍如圖3所示。從圖3中可以看出，靜態(tài)條件下戰(zhàn)斗部的毀傷半徑在80 m以上，最大至86 m，在此距離內(nèi)能保證至少有1枚破片命中TBM有效載荷。

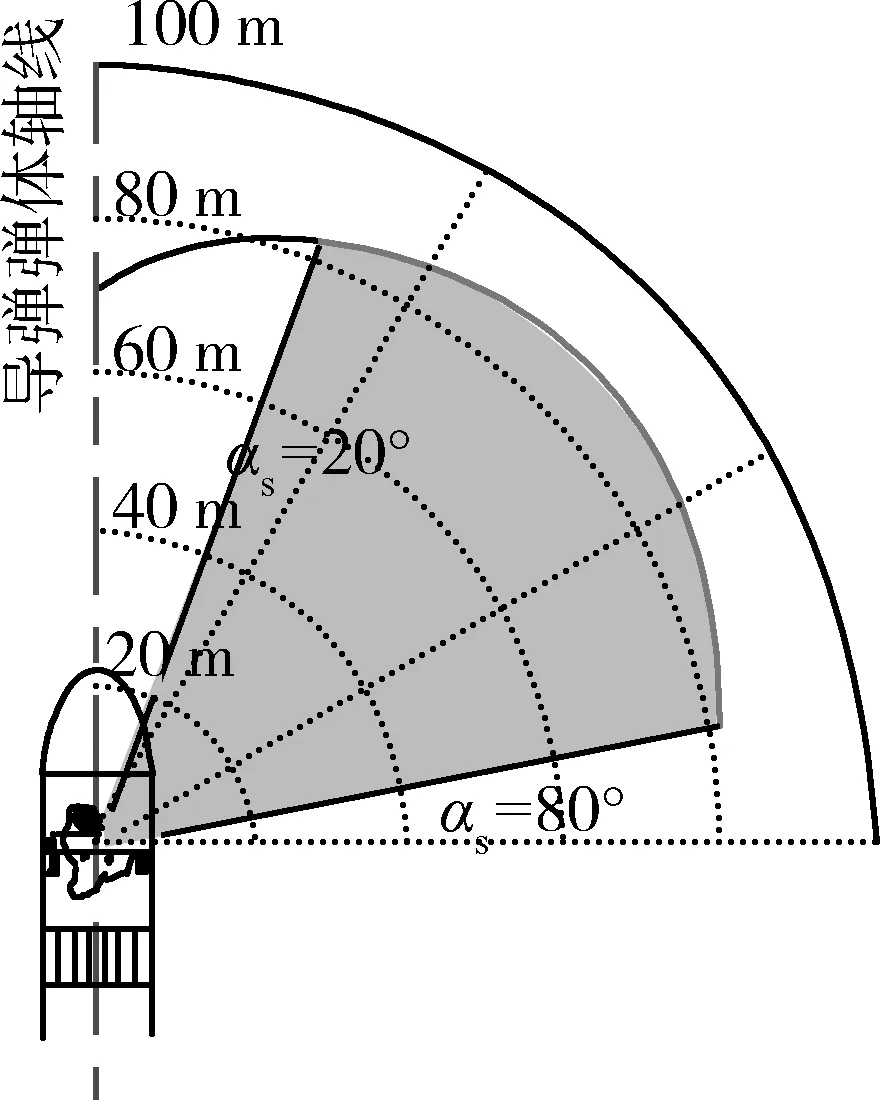
圖3 瞄準(zhǔn)式前向戰(zhàn)斗部的靜態(tài)威力場范圍Fig.3 Damage range of gimbaled forward-firing warhead at static condition

2 最佳起爆距離與起爆延時(shí)

引信探測到目標(biāo)后，根據(jù)彈目交會條件的不同，通常都會延遲一定時(shí)間起爆，以獲得最佳毀傷效果。本節(jié)首先確定最佳起爆距離，然后求出起爆延時(shí)。

2.1 最佳起爆距離

起爆距離定義為爆炸時(shí)戰(zhàn)斗部中心與目標(biāo)中心的距離。破片靜態(tài)速度vf與彈目相對速度vr合成后，飛散角會發(fā)生變化，設(shè)破片束動態(tài)飛散錐角為θd，起爆距離為D，則撞擊目標(biāo)時(shí)垂直于破片束軸線的擴(kuò)散圓半徑

ρ=Dtanθd/2.

(1)

由于戰(zhàn)斗部瞄準(zhǔn)方向與vr方向近似相同，故式(1)可表示為

(2)

式中：θs為破片束靜態(tài)飛散錐角。

瞄準(zhǔn)式戰(zhàn)斗部對目標(biāo)的毀傷概率可以表示為

Pk=PinPd，

(3)

式中：Pin為目標(biāo)落入破片擴(kuò)散圓內(nèi)的概率；Pd為落入后被毀傷的概率。

如果擴(kuò)散圓半徑過大，會導(dǎo)致破片過于稀疏，目標(biāo)有可能從破片間縫隙中“溜走”，使Pd急劇下降；而擴(kuò)散圓半徑太小，則會增加瞄準(zhǔn)難度，降低落入概率Pin。這2種情況是相互矛盾的，因此破片群與目標(biāo)相遇時(shí)，存在一個(gè)最佳的擴(kuò)散半徑ρop，文獻(xiàn)[5]求解出最佳擴(kuò)散圓半徑為

(4)

式中：N為有效破片個(gè)數(shù)；Aρ(為目標(biāo)易損面積；σ為脫靶量的標(biāo)準(zhǔn)差。

由式(2),(4)可得最佳起爆距離

(5)

式中：目標(biāo)類型和易損面積Aρ在導(dǎo)彈發(fā)射時(shí)已經(jīng)確定；破片個(gè)數(shù)N、破片束靜態(tài)飛散錐角θs、破片靜態(tài)初速vf由戰(zhàn)斗部決定；彈目相對速度vr可通過導(dǎo)引頭測得；脫靶量標(biāo)準(zhǔn)差σ由制導(dǎo)系統(tǒng)決定。

2.2 最佳起爆延時(shí)

借鑒美國海軍AD報(bào)告[7]延時(shí)模型的思路，利用導(dǎo)引頭失效前某一時(shí)刻所測參數(shù)和引信探測到目標(biāo)初始時(shí)刻所測參數(shù)，計(jì)算目標(biāo)剩余飛行時(shí)間，結(jié)合最佳起爆距離的結(jié)論，求出戰(zhàn)斗部最佳起爆延時(shí)時(shí)間。

以戰(zhàn)斗部中心O為原點(diǎn)建立彈體坐標(biāo)系Oxmymzm，如圖4所示，導(dǎo)引頭中心O'到戰(zhàn)斗部中心的距離為a。彈目交會時(shí)間很短，導(dǎo)彈和目標(biāo)來不及機(jī)動，可認(rèn)為都作勻速直線運(yùn)動，設(shè)目標(biāo)沿直線Q0Q1飛行。Q0為導(dǎo)引頭失效前某一時(shí)刻所測得的目標(biāo)中心位置，Q1為引信剛探測到目標(biāo)時(shí)的目標(biāo)位置，之后經(jīng)延時(shí)τ，目標(biāo)運(yùn)動到最佳距離Qop處，戰(zhàn)斗部起爆，在Qb處破片高速撞擊目標(biāo)并將其毀傷。

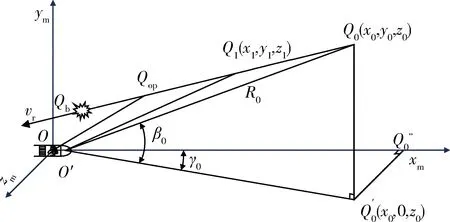
圖4 彈目交會模型Fig.4 Model of missile-target encounter

Q0,Q1點(diǎn)的坐標(biāo)可表示為

(6)

(7)

式中：R為目標(biāo)與導(dǎo)引頭中心的距離；β，γ分別為目標(biāo)的俯仰角和方位角，這些參量可以通過導(dǎo)引頭或引信測得。

R0+aarccosβ0arccosγ0.

(8)

D1=R1+aarccosβ1arccosγ1.

(9)

在相對速度與戰(zhàn)斗部中心-目標(biāo)中心連線所組成的平面內(nèi)，令兩者的夾角為φ，如圖5所示。目標(biāo)從Q0運(yùn)動到Q1所用的時(shí)間為t1，根據(jù)余弦定理

(10)

再經(jīng)過時(shí)間τ，目標(biāo)運(yùn)動到Qop處，根據(jù)余弦定理，在△OQ0Qop中有

(11)

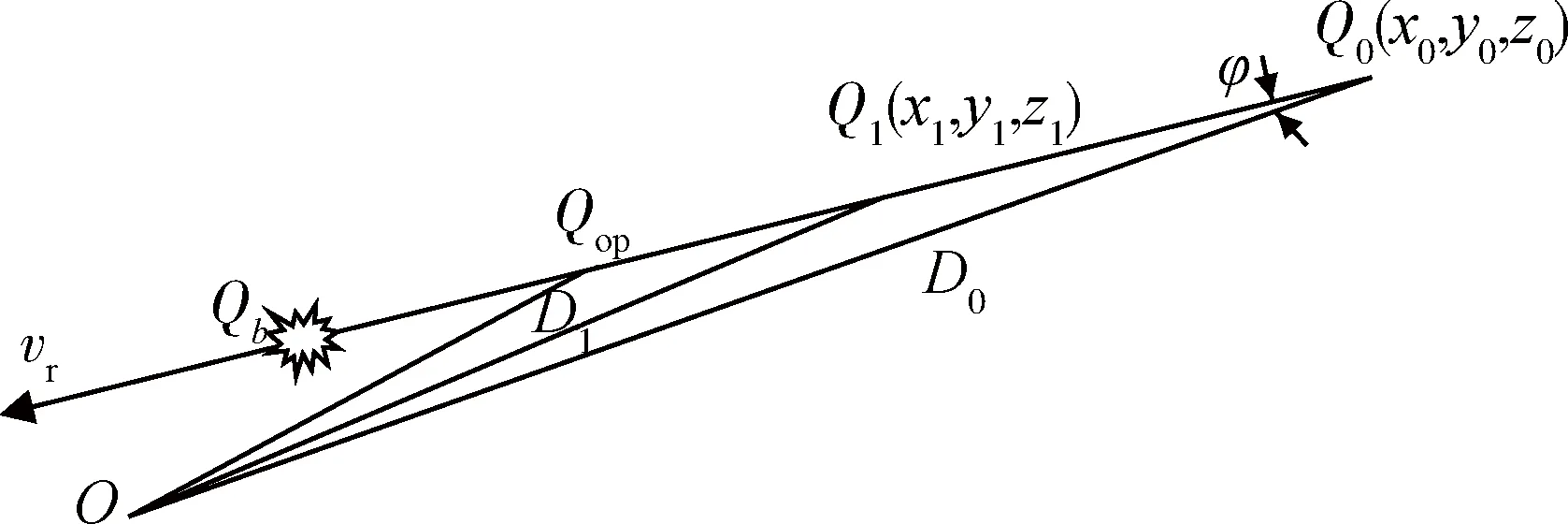
圖5 用于計(jì)算起爆延時(shí)的三角形Fig.5 Triangles used for calculating optimal delay time

聯(lián)立式(6)～(11)可求出起爆延時(shí)τ。即引信探測到目標(biāo)后經(jīng)延時(shí)τ起爆戰(zhàn)斗部，可獲得最好的毀傷效果。

3 仿真與分析

彈目交會時(shí)，目標(biāo)的位置參數(shù)、交會姿態(tài)、彈目相對速度等都會影響起爆延時(shí)時(shí)間。本節(jié)主要分析彈目相對速度、破片靜態(tài)飛散角對最佳起爆延時(shí)的影響。

3.1 相對速度與起爆延時(shí)的關(guān)系

在導(dǎo)彈坐標(biāo)系中先設(shè)置一條目標(biāo)運(yùn)動軌跡，設(shè)導(dǎo)引頭探測到的目標(biāo)中心點(diǎn)位置Q0(600,100,100)，引信剛探測到目標(biāo)時(shí)的位置Q1(280,60,60)。仿真計(jì)算時(shí)，令破片數(shù)N=200，破片靜態(tài)初速為vf=1 000 m/s，導(dǎo)引頭中心與戰(zhàn)斗部中心的距離為a=1 m，脫靶量標(biāo)準(zhǔn)差σ=3 m，目標(biāo)易損面積為Aρ=0.6 m2。當(dāng)破片束靜態(tài)錐角θs分別為10°，15°，20°，30°時(shí)，最佳起爆延時(shí)τ隨彈目相對速度vr的變化曲線如圖6所示。由圖6可以看出：①當(dāng)θs一定時(shí)，起爆延時(shí)τ隨vr的增加而縮短；②同一彈目相對速度條件下，破片束靜態(tài)錐角越大，延時(shí)時(shí)間越長。

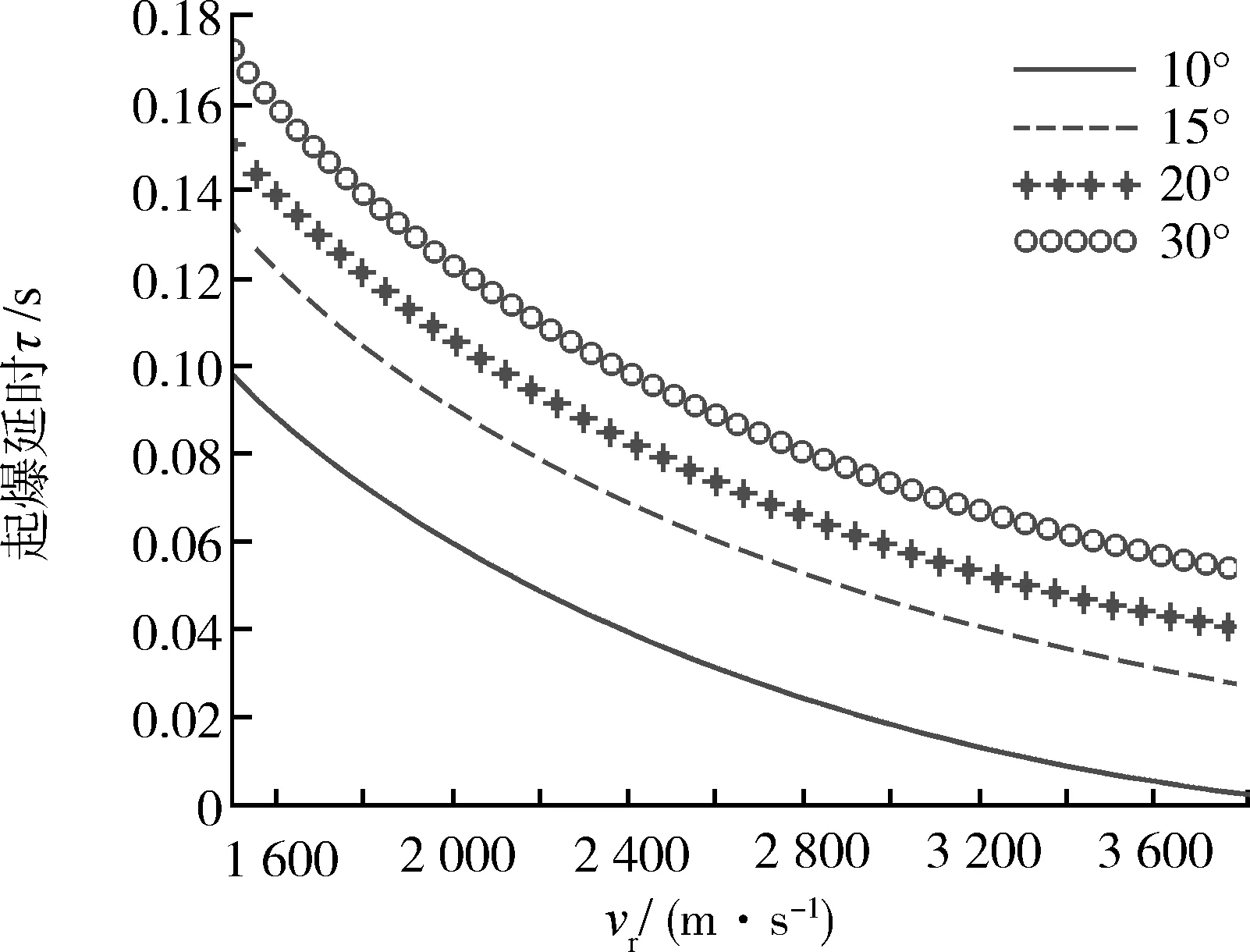
圖6 起爆延時(shí)τ隨彈目相對速度vr的變化曲線Fig.6 τ - vr curves when θs in different values

起爆延時(shí)的仿真結(jié)果與實(shí)際變化情況是一致的。首先，vr越大，目標(biāo)從進(jìn)入引信探測范圍到飛至最佳起爆距離處的時(shí)間就越短，起爆延時(shí)也就越短；vr相同時(shí)，θs越大，破片束擴(kuò)散就越快，戰(zhàn)斗部的最佳起爆距離就越小，最佳起爆位置與引信探測到目標(biāo)初始位置之間的距離就越大，目標(biāo)需要更長時(shí)間才可到達(dá)，故起爆延時(shí)更長。

3.2 破片束靜態(tài)錐角與起爆延時(shí)的關(guān)系

為進(jìn)一步明確θs對起爆延時(shí)的影響，在其他條件不變的情況下，令彈目相對速度vr=3 000 m/s，計(jì)算出起爆延時(shí)τ隨θs的變化曲線如圖7所示。從該曲線可分析出以下結(jié)論：

電壓控制策略目的是即時(shí)調(diào)節(jié)區(qū)域電網(wǎng)中低壓側(cè)電壓以及控制區(qū)域整體電壓水平，使得電壓穩(wěn)定在一定的區(qū)間內(nèi)[6]。低壓側(cè)電壓低，高壓側(cè)電壓高時(shí)，首先上調(diào)主變檔位，其次投入電容器；低壓側(cè)電壓低，高壓側(cè)電壓正常，首先投入電容器，其次上調(diào)主變檔位；低壓側(cè)電壓高，高壓側(cè)電壓高，首先切除電容器，其次下調(diào)主變檔位；低壓側(cè)電壓高，電網(wǎng)負(fù)荷下降時(shí)，首先切除電容器，其次下調(diào)主變檔位；低壓側(cè)電壓高，且高壓側(cè)電壓正常、電網(wǎng)負(fù)荷穩(wěn)定，首先下調(diào)主變檔位，其次切除電容器[7]。

(1)τ隨θs的增大而變大，當(dāng)θs比較小時(shí)，τ增加較快，當(dāng)破片束靜態(tài)錐角θs增大到一定程度時(shí)，τ增速變慢；

(2) 當(dāng)θs=8.2°時(shí)，延時(shí)時(shí)間為0，說明計(jì)算得出的最佳起爆距離等于引信探測距離，引信探測到目標(biāo)時(shí)立即控制戰(zhàn)斗部起爆；

(3) 當(dāng)θs<8.2°時(shí)τ為負(fù)值，說明引信探測到目標(biāo)之前目標(biāo)就已經(jīng)達(dá)到了最佳起爆距離處，這顯然是不合理的，所以戰(zhàn)斗部設(shè)計(jì)時(shí)應(yīng)使破片束靜態(tài)錐角θs≥8.2°。

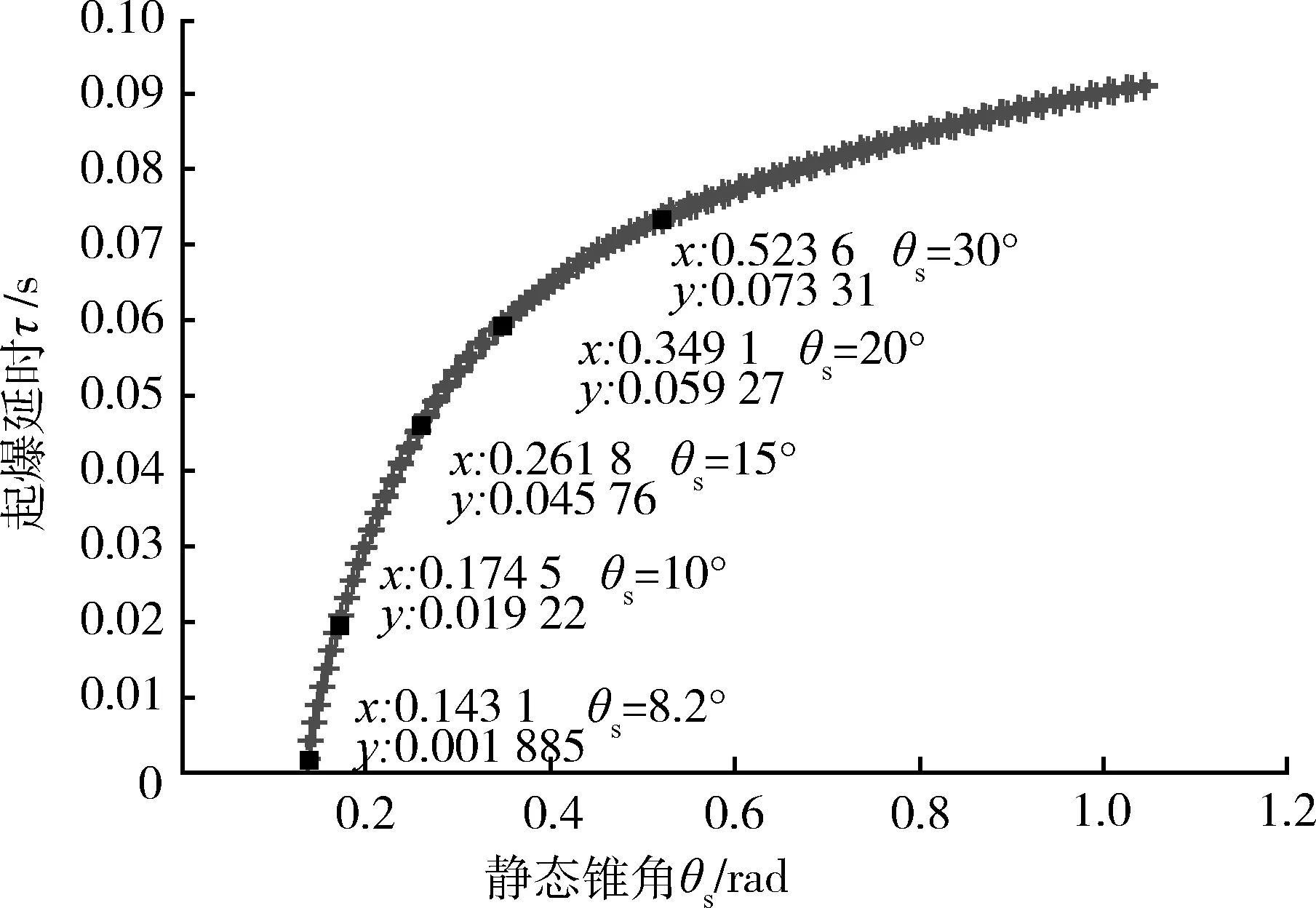
圖7 vr=3 000 m/s時(shí)τ隨 s的變化曲線Fig.7 τ-s curve when vr is 3 000 m/s

4 結(jié)束語

本文在靜爆試驗(yàn)數(shù)據(jù)的基礎(chǔ)上，通過適當(dāng)假設(shè)和簡化，建立了瞄準(zhǔn)式戰(zhàn)斗部最佳起爆延時(shí)的模型并進(jìn)行了仿真計(jì)算，驗(yàn)證了模型的正確性。計(jì)算得出，為避免引信探測到目標(biāo)前目標(biāo)就運(yùn)動到最佳起爆距離處，破片束靜態(tài)錐角θs應(yīng)大于等于8.2°。解決實(shí)際問題時(shí)，針對不同的戰(zhàn)斗部、目標(biāo)及交會條件，可參考本文的模型確定破片束錐角的范圍。

本文在研究時(shí)進(jìn)行了適當(dāng)假設(shè)和簡化，比如在轉(zhuǎn)角為20°～80°時(shí)忽略了導(dǎo)彈前部部件對破片飛散的遮擋，在一定冗余系數(shù)情況下認(rèn)為著靶破片分布均勻，認(rèn)為單枚破片在動態(tài)條件下撞擊目標(biāo)可毀傷其有效載荷等，這些方面還需要通過計(jì)算、仿真和試驗(yàn)深入研究。

參考文獻(xiàn)：

[1] 張志鴻. 俄羅斯現(xiàn)代防空導(dǎo)彈體系的發(fā)展[J]. 現(xiàn)代防御技術(shù)，2002，30(2)：1-14.

ZHANG Zhi-hong. Development of Russian Modern Air-Defence Missile Systems[J]. Modern Defence Technology, 2002，30(2)：1-14.

[2] 曹海江，劉銘，王威. 地空導(dǎo)彈抗擊TBM殺傷區(qū)仿真研究[J]. 現(xiàn)代防御技術(shù)，2008，36(4)：19-23.

CAO Hai-jiang, LIU Ming, WANG Wei. Research on the Damage Zone of SAM Intercepting the Tactical Ballistic Missile[J]. Modern Defence Technology, 2008，36(4)：19-23.

[3] Richard M Lloyd. Physics of Direct Hit and Near Miss Warhead Technology[M]. Alexander Bell Drive, Reston, Virginia: American Institute of Aeronautics and Astronautics, Inc. 2001:246-251.

[4] Richard M Lloyd. Conventional Warhead System Physics and Engineering Design[M]. Alexander Bell Drive, Reston, Virginia: American Institute of Aeronautics and Astronautics, Inc. 14 December, 2001:193-225.

[5] 莊志洪，王宏波，張清泰. 一種反彈道導(dǎo)彈用瞄準(zhǔn)戰(zhàn)斗部的引戰(zhàn)能力分析[J]. 探測與控制學(xué)報(bào)，2002，24(3)：1-4.

ZHUANG Zhi-hong, WANG Hong-bo, ZHANG Qing-tai. Ability Analysis of Gimbaled Warhead in Anti-Tactical Ballistic Missile[J]. Journal of Detection & Control, 2002,24(3):1-4.

[6] 盧芳云，李翔宇，林玉亮. 戰(zhàn)斗部結(jié)構(gòu)與原理[M]. 北京：科學(xué)出版社，2009.

LU Fang-yun，LI Xiang-yu，LIN Yu-liang. Warhead Structure and Rationale[M]. Beijing: Science Press,2009.

[7] Bruce A， Hall Frank J Langley. Office of Naval Research[R]. AD—B010399，28 JANUARY 1976.

[8] 楊朝. 一種美國延時(shí)模型的分析與推導(dǎo)[C]∥第12屆引信學(xué)術(shù)年會，昆明，2001：272-276.

YANG Chao. The Analyse and Deduction of a Delay Model[C]∥12th Academic Convention of Fuze，Kunming，2001：272-276.

[9] GJB5232.2-2004，戰(zhàn)術(shù)導(dǎo)彈戰(zhàn)斗部靶場試驗(yàn)方法第2部分：靜爆試驗(yàn)破片飛散特性測試[S].北京：國防科學(xué)技術(shù)工業(yè)委員會，2004.

GJB5232.2-2004，Test Method for Arena of Tactical Missile Warhead Performance-Part 2: Determination of Dispersing Characteristic of Fragment in Fixed Point Explosion Test[S].Beijing:COSTIND, 2004.

[10] GJB5232.3-2004，戰(zhàn)術(shù)導(dǎo)彈戰(zhàn)斗部靶場試驗(yàn)方法第2部分：靜爆試驗(yàn)破片初速測試[S].北京：國防科學(xué)技術(shù)工業(yè)委員會，2004.

GJB5232.3-2004，Test Method for Arena of Tactical Missile Warhead Performance-Part 2: Determination of Fragment Initial Velocity in Fixed Point Explosion Test[S].Beijing:COSTIND, 2004.

[11] 王樹山, 李朝君, 馬曉飛，等. 鎢合金破片對屏蔽裝藥撞擊起爆的實(shí)驗(yàn)研究[J].兵工學(xué)報(bào)， 2001，22(2):189-191.

WANG Shu-shan, LI Chao-jun, MA Xiao-fei, et al. An Experimental Study on The Initiation of Covered Charge Impacted By Tungsten Alloy Fragments[J]. Acta Armamentarii. 2001,22(2):189-191.

[12] 馬曉飛，李園，徐豫新，等，破片對薄蓋板裝藥的沖擊起爆研究[J].彈箭與制導(dǎo)學(xué)報(bào)，2009，29(5)：133-138.

MA Xiao-fei，LI Yuan，XU Yu-xin, et al. Research on Fragment Impact Initiation of the Charge Covered with a Thin Plate[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009，29(5)：133-138.

[13] 馬曉飛，徐豫新，李園,等.破片對模擬聚能戰(zhàn)斗部裝藥沖擊起爆研究[J]. 戰(zhàn)術(shù)導(dǎo)彈技術(shù)，2010(2)：29-32.

MA Xiao-fei，XU Yu-xin，LI Yuan, et al. Research on Fragment Impact Initiation of Simulating Charge of Shaped Charge Warhead[J]. Tactical Missiles Technology, 2010(2)：29-32.