基于貝葉斯網(wǎng)絡(luò)的目標(biāo)選擇方案設(shè)計*

賀小亮,畢義明

(1.國防大學(xué) 研究生學(xué)院，北京 100091；2.第二炮兵工程大學(xué) 初級指揮學(xué)院，陜西 西安 710025)

0 引言

目標(biāo)選擇[1-2]是指依據(jù)聯(lián)合火力戰(zhàn)的作戰(zhàn)目的，對戰(zhàn)場目標(biāo)進行分析、計算、對比，從中挑選出最佳打擊目標(biāo)的活動。美軍在《目標(biāo)選擇與聯(lián)合打擊條令》中指出，目標(biāo)選擇就是選擇目標(biāo)、排列目標(biāo)的優(yōu)先順序。信息化條件下戰(zhàn)場環(huán)境更加復(fù)雜，可打擊的目標(biāo)類型和數(shù)量越來越多，目標(biāo)之間相互作用構(gòu)成復(fù)雜的目標(biāo)體系，從而為目標(biāo)選擇帶來了嚴重的挑戰(zhàn)。

貝葉斯網(wǎng)絡(luò)是近幾十年來人工智能領(lǐng)域中最重要的研究成果之一，它能夠根據(jù)不確定或不完整的信息，使用概率論來處理不同知識成分之間的條件相關(guān)而產(chǎn)生的不確定性，提供了一種將知識直覺地圖解化的方法，是一種新的知識表示模型[3-5]。貝葉斯網(wǎng)絡(luò)作為一種可描述不確定信息的專家系統(tǒng)，非常適合對目標(biāo)體系中各類目標(biāo)之間的不確定關(guān)系進行推理決策。根據(jù)貝葉斯網(wǎng)絡(luò)的特點，本文對基于貝葉斯網(wǎng)絡(luò)的目標(biāo)選擇方法進行了初步探索，敘述了目標(biāo)選擇貝葉斯網(wǎng)絡(luò)模型的建立和仿真過程。

1 目標(biāo)選擇的概念描述

1.1 目標(biāo)體系

定義1 不同的單個目標(biāo)(也可稱為子系統(tǒng)、元素和部分)按照某一運行機制相互作用形成一個有機的整體，發(fā)揮出某種功能，稱之為目標(biāo)系統(tǒng)[6]。不同的目標(biāo)系統(tǒng)功能不同，它們之間的相互作用同樣形成一個有機的整體，稱之為目標(biāo)體系(target in system of systems, TSS)。

本文在更高層次和更大范圍將2個范疇引入目標(biāo)體系的概念，強調(diào)目標(biāo)體系由多個目標(biāo)系統(tǒng)組成。為了研究問題方便，根據(jù)相似性原理，將目標(biāo)體系劃分為3級層次，目標(biāo)體系包括目標(biāo)系統(tǒng)，目標(biāo)系統(tǒng)又可以由單個目標(biāo)組成，如圖1所示。可以看出，目標(biāo)體系具有多層次性和多側(cè)面性特點。目標(biāo)體系各要素在縱向上存在著不同等級的層次關(guān)系，其中低一級的要素是高一級要素的基礎(chǔ)和有機組成部分。目標(biāo)體系的某一層上，又可以從橫向上把各要素區(qū)分為若干互相聯(lián)系、互相制約、互相作用的部分[7]。

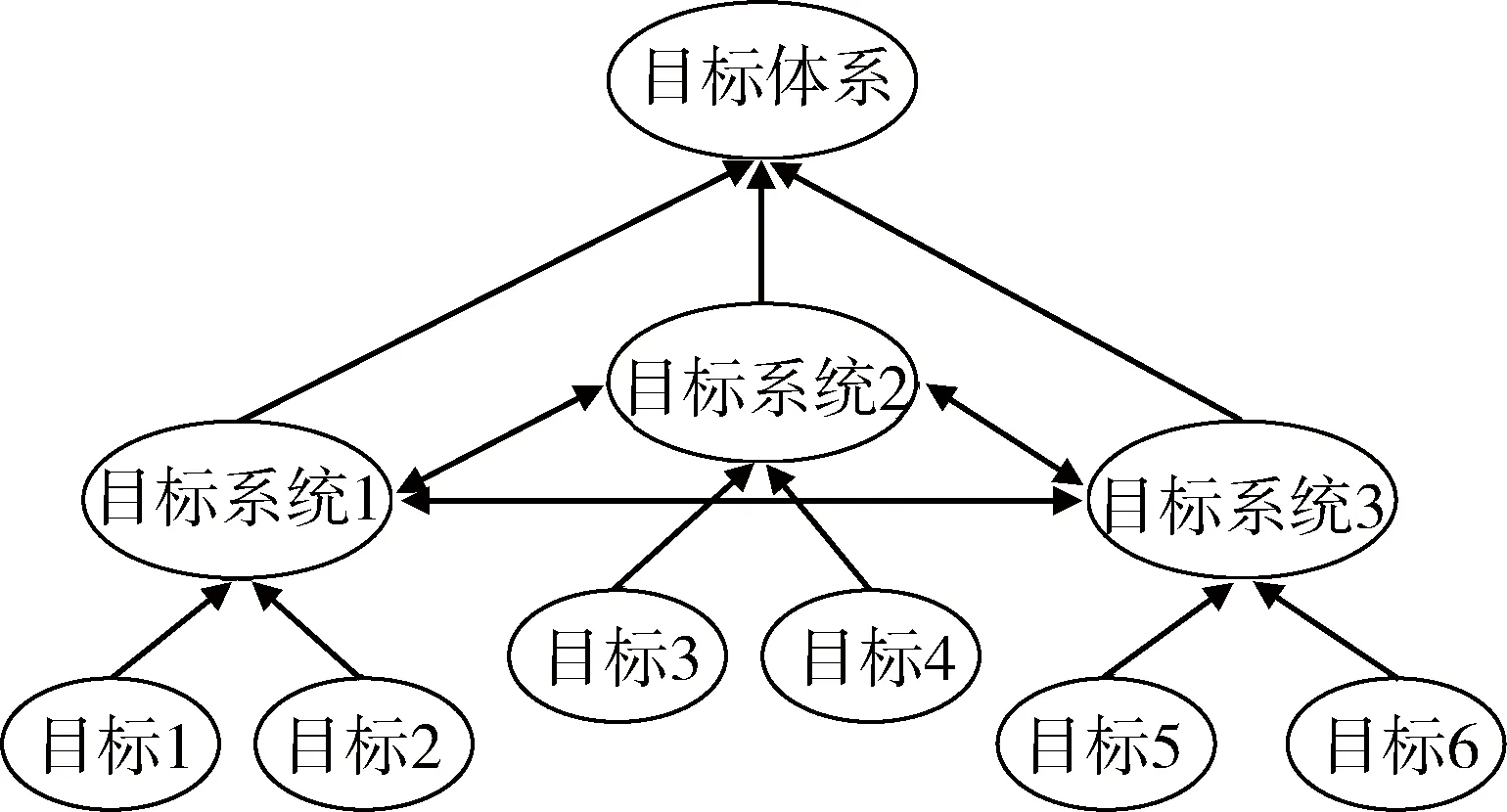
圖1 目標(biāo)體系層次結(jié)構(gòu)Fig.1 TSS architecture

1.2 目標(biāo)選擇

在打擊目標(biāo)體系時，需要考慮體系的支撐點和關(guān)鍵點，打擊行動的效果以對體系整體影響效果為衡量，表現(xiàn)為目標(biāo)體系的崩潰或在體系效能上得到降低[8]。

定義2 目標(biāo)選擇：根據(jù)作戰(zhàn)目的，運用目標(biāo)體系分析理論，找出目標(biāo)體系中起支撐作用的重點目標(biāo)作為打擊對象。

因此，目標(biāo)選擇就是分析和比較目標(biāo)體系中的各類目標(biāo)對實現(xiàn)我方戰(zhàn)略或戰(zhàn)役目的的相對重要程度，找出體系中的關(guān)鍵目標(biāo)作為重點打擊的對象。

2 基于貝葉斯網(wǎng)絡(luò)的目標(biāo)選擇模型

2.1 貝葉斯網(wǎng)絡(luò)

貝葉斯網(wǎng)絡(luò)[8-9]是一種對概率關(guān)系的有向圖解描述，提供了一種自然的表示事物間因果關(guān)系的方法，是綜合利用概率論和圖論進行不確定事件分析和推理的工具。一個貝葉斯網(wǎng)絡(luò)由網(wǎng)絡(luò)結(jié)構(gòu)G和網(wǎng)絡(luò)參數(shù)θ兩部分組成。即

B=〈G,θ〉.

網(wǎng)絡(luò)結(jié)構(gòu)G就是用一個有向無環(huán)圖(directed acyclic graph, DAG)對變量進行編碼，它的節(jié)點表示隨機變量vi，弧表示變量之間的相互聯(lián)系，節(jié)點變量可以是任何問題的抽象。有向圖蘊含了條件獨立性假設(shè)，貝葉斯網(wǎng)絡(luò)規(guī)定圖中的每個節(jié)點vi條件獨立于由vi的父節(jié)點給定的非vi后代節(jié)點構(gòu)成的任何節(jié)點子集。假設(shè)A(vi)表示非vi的后代節(jié)點子集，B(vi)表示vi的直接雙親節(jié)點，則

P(viA(vi),B(vi))=P(viB(vi)).

網(wǎng)絡(luò)參數(shù)θ用條件概率表(conditional probability table,CPT)來表示，CPT表達了節(jié)點變量與其父節(jié)點之間的概率關(guān)系，沒有任何父節(jié)點的節(jié)點的條件概率為其先驗概率。

有了節(jié)點及其相互關(guān)系、條件概率表，貝葉斯網(wǎng)絡(luò)就可以表達網(wǎng)絡(luò)中所有節(jié)點的聯(lián)合概率，并可以根據(jù)先驗概率和某些節(jié)點的取值計算其他任意節(jié)點的概率信息。給定一個隨機變量集V=(v1,v2,…,vn)，由概率論的鏈式規(guī)則可得變量vi(i=1,2,…,n)的聯(lián)合概率為

2.2 網(wǎng)絡(luò)結(jié)構(gòu)的確定

根據(jù)目標(biāo)體系的內(nèi)部結(jié)構(gòu)及貝葉斯網(wǎng)絡(luò)的規(guī)則，來確定網(wǎng)絡(luò)結(jié)構(gòu)，形式類似于圖1。網(wǎng)絡(luò)結(jié)構(gòu)能反映出目標(biāo)體系的內(nèi)在聯(lián)系情況。為了方便、高效地得出各類型目標(biāo)對目標(biāo)體系效能的相對影響程度，將所有節(jié)點的狀態(tài)設(shè)為2種：強(strong，S)、弱(weak，W)，分別表示節(jié)點目標(biāo)受到打擊后所屬能力沒有損失和基本完全損失[10]。

2.3 條件概率表的構(gòu)造

貝葉斯網(wǎng)絡(luò)結(jié)構(gòu)建立之后，下一個重要的任務(wù)就是給定節(jié)點的條件概率分布。條件概率的確定需要大量的數(shù)據(jù)統(tǒng)計和專家知識作為支撐。為了有效地發(fā)揮兩者的作用，本文采用加權(quán)和算法獲取節(jié)點的條件概率分布。以圖2為例，計算節(jié)點U的條件概率。

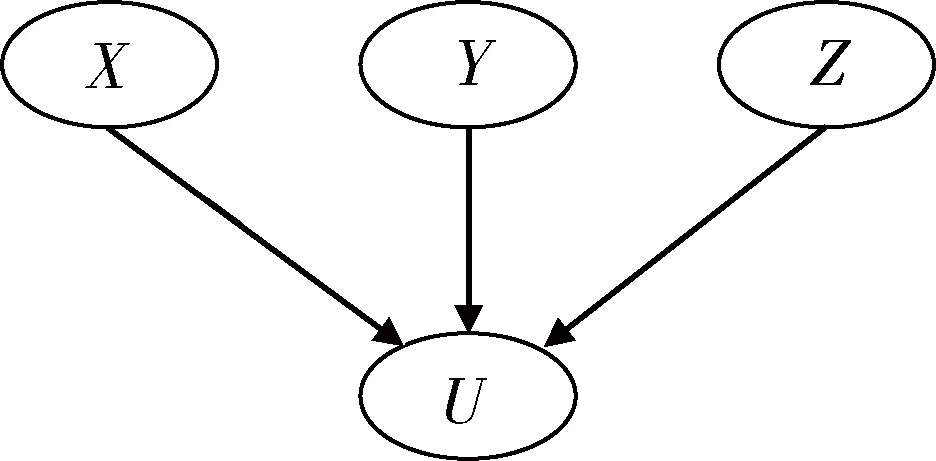
圖2 網(wǎng)絡(luò)結(jié)構(gòu)示例Fig.2 Network structure sample

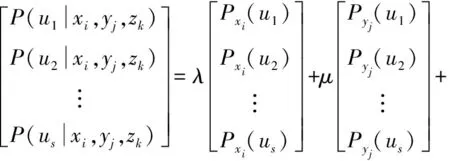
(1)

式中：Pyj(us)為子節(jié)點Y在狀態(tài)yj時，父節(jié)點U處于狀態(tài)us的條件概率，即Pyj(us)=P(usyj)。

式(1)表示節(jié)點U的條件概率計算過程，(λ，μ，ν)分別是子節(jié)點X，Y，Z對于父節(jié)點U的權(quán)重系數(shù)，并且λ+μ+ν=1,0≤λ,μ,ν≤1。這里，Pyj是通過大量的數(shù)據(jù)學(xué)習(xí)得到的，(λ，μ，ν)是專家依據(jù)自身經(jīng)驗判斷得到的。貝葉斯網(wǎng)絡(luò)一個卓越的性能就在于其強大的學(xué)習(xí)能力，無論條件概率還是網(wǎng)絡(luò)的結(jié)構(gòu)都能夠通過數(shù)據(jù)學(xué)習(xí)進行更新。在給定每個節(jié)點的初始概率之后，就可以通過貝葉斯網(wǎng)絡(luò)的推理算法獲得每個節(jié)點所有可能狀態(tài)的概率分布。

2.4 模型的計算過程

在目標(biāo)體系的網(wǎng)絡(luò)結(jié)構(gòu)和條件概率表確定后，需要更新節(jié)點的數(shù)據(jù)，找出關(guān)鍵目標(biāo)并排列目標(biāo)的順序，形成目標(biāo)選擇方案。目標(biāo)的選擇過程分為2個階段：

第1階段，將所有的目標(biāo)狀態(tài)更新為最強(strongest)，根據(jù)貝葉斯網(wǎng)絡(luò)的推理結(jié)果，可得到目標(biāo)體系的最強狀態(tài)概率。

Pmax=P(TSS=strongestAllTargets=strongest)

第2階段，將其中目標(biāo)Ti的狀態(tài)更新為最弱(weakest)，其他目標(biāo)仍為最強狀態(tài)，此時，可得到目標(biāo)體系狀態(tài)的更新概率。

PTi=P(TSS=strongest|Ti=weakest,

Remain=strongest).

那么，目標(biāo)Ti相比于其他目標(biāo)對目標(biāo)體系的相對影響度(relative impact, RI)為

(2)

隨后，依次將其他目標(biāo)按照第2階段要求進行數(shù)據(jù)更新，得到RI。根據(jù)計算結(jié)果，對所有目標(biāo)排序，形成目標(biāo)選擇方案。

3 實例仿真應(yīng)用

以奪取藍方制空權(quán)為例，來驗證目標(biāo)選擇貝葉斯網(wǎng)絡(luò)模型的可行性和有效性。為奪取制空權(quán)，即要摧毀藍方防空力量體系。防空力量體系是由多目標(biāo)系統(tǒng)及多類型目標(biāo)構(gòu)成的，為提高打擊效果，節(jié)省紅方彈藥消耗，以摧毀防空力量體系的整體效能為目的，將體系內(nèi)目標(biāo)進行排序，找出關(guān)鍵目標(biāo)，供指揮機構(gòu)決策。按照1.1節(jié)的目標(biāo)體系劃分原則，對防空力量目標(biāo)體系進行劃分。經(jīng)查閱資料[11-12]，防空力量目標(biāo)體系(air defense TSS, ADTSS)主要是由防空指揮控制系統(tǒng)(air defense command and control system, ADCCS)，防空雷達系統(tǒng)(air defense radar system, ADRS)，空軍基地(air base, AB)，地對空導(dǎo)彈系統(tǒng)(ground to air missile system, GAMS)，高炮系統(tǒng)(antiaircraft gun system, AGS)等系統(tǒng)組成。防空指揮控制系統(tǒng)主要由指揮機構(gòu)(command agency, CA)，通信樞紐(communication center, CC)等目標(biāo)組成；防空雷達系統(tǒng)是由管報中心(control and reporting center,CRC)，管報站(control and reporting post,CRP)，雷達站(radar post,RP)等目標(biāo)組成；空軍基地的主要目標(biāo)有：跑道(runway)，飛機(aircraft)，油料(petrol oil lubricant, POL)等。地對空導(dǎo)彈系統(tǒng)包括的主要目標(biāo)是地對空導(dǎo)彈陣地(ground to air missile position, GAMP)。高炮系統(tǒng)包括的主要目標(biāo)是高炮陣地(antiaircraft gun position, AGP)。根據(jù)防空力量目標(biāo)體系的組織結(jié)構(gòu)和內(nèi)部關(guān)系，以軟件Netcia為仿真平臺，構(gòu)建網(wǎng)絡(luò)結(jié)構(gòu)，如圖3所示。

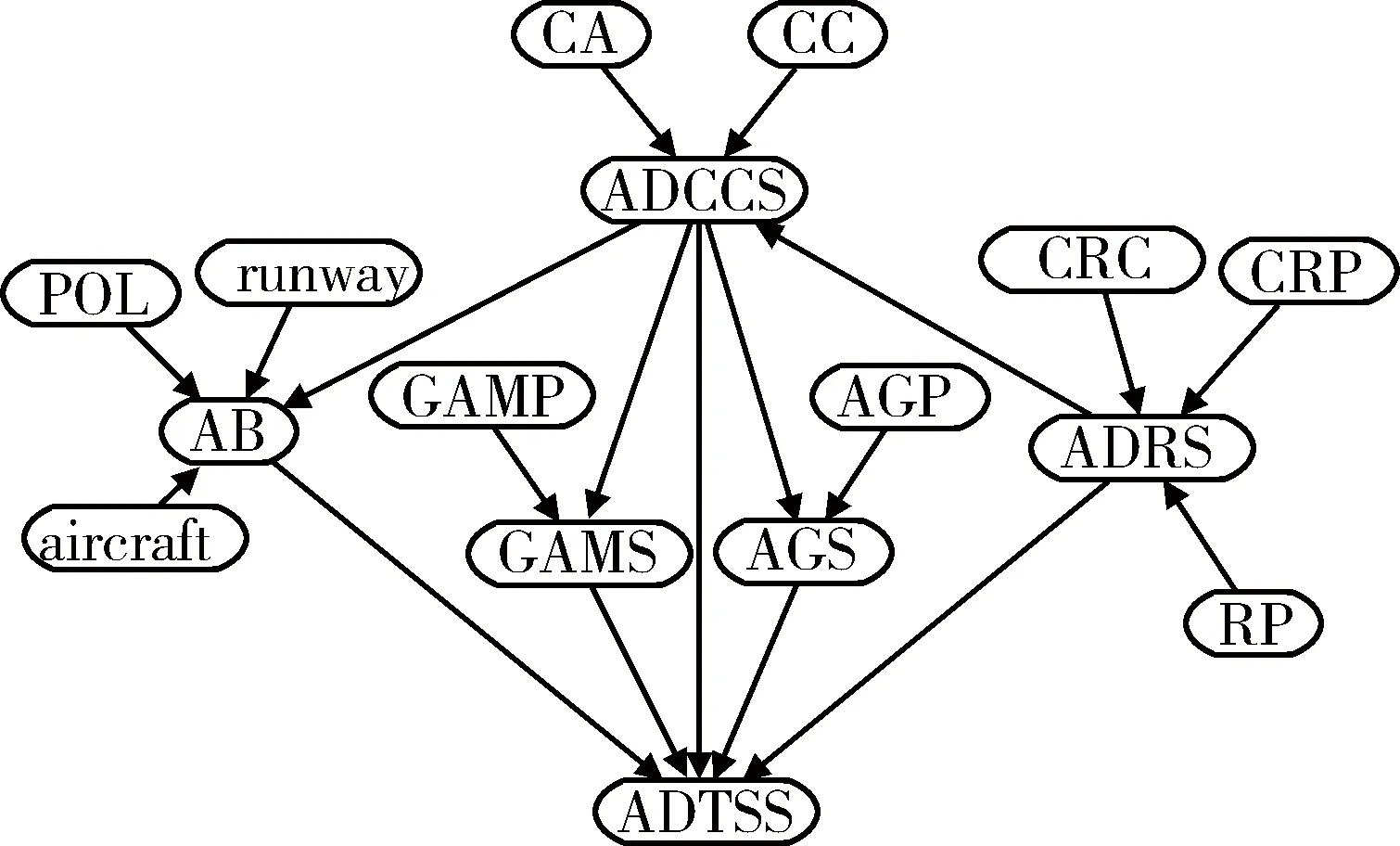
圖3 防空力量目標(biāo)體系網(wǎng)絡(luò)結(jié)構(gòu)Fig.3 Air defense TSS network structure

根據(jù)2.3節(jié)節(jié)點條件概率獲取方法，利用歷史數(shù)據(jù)統(tǒng)計和專家知識，通過參數(shù)學(xué)習(xí)，確定網(wǎng)絡(luò)中節(jié)點的條件概率。以空軍基地(air base)為例，其子節(jié)點分別是油料(POL)，跑道(runway)，飛機(aircraft)，防空指揮控制系統(tǒng)(ADCCS)。設(shè)定子節(jié)點對應(yīng)父節(jié)點的權(quán)重系數(shù)為(λ=0.05，μ=0.5，ν=0.3，β=0.15)，空軍基地(air base)對應(yīng)其每個子節(jié)點的狀態(tài)條件概率，如表1所示。

將表1中的數(shù)據(jù)和子節(jié)點的權(quán)重系數(shù)，按照式

(1)計算得出空軍基地對應(yīng)其子節(jié)點的條件概率，如表2所示。

同理，計算得出其他節(jié)點目標(biāo)的條件概率表。將所得條件概率數(shù)據(jù)，按要求輸入以軟件Netcia為仿真平臺構(gòu)建的防空力量體系網(wǎng)絡(luò)結(jié)構(gòu)中，然后按照2.4節(jié)模型計算過程的第1階段要求，將網(wǎng)絡(luò)中目標(biāo)節(jié)點的狀態(tài)更新為最強，得到體系更新狀態(tài)概率Pmax=77.1%，如圖4所示。

根據(jù)模型計算過程的第2階段要求，依次將目標(biāo)節(jié)點的狀態(tài)更新為最弱，得到對應(yīng)目標(biāo)體系節(jié)點(ADTSS)更新結(jié)果PTi(圖5是將跑道節(jié)點狀態(tài)更新為最弱時的網(wǎng)絡(luò)更新結(jié)果)，再按照式(2)，將每個目標(biāo)對體系的相對影響度計算出來，見表3。其中，指揮機構(gòu)(CA)，管報中心(CRC)，地對空導(dǎo)彈陣地(GAMP)，跑道(runway)排在前4位，表明這是對防空力量體系效能有重要作用的目標(biāo)，應(yīng)進行重點打擊。對防空力量體系進行打擊時，可按照表3中的結(jié)果選擇目標(biāo)，制定打擊目標(biāo)清單。

表1 空軍基地對應(yīng)其每個子節(jié)點的條件概率表Table 1 CPT of each child node of air base

表2 空軍基地對應(yīng)其子節(jié)點的條件概率表Table 2 CPT of child node of air base

表3 目標(biāo)相對影響度Table 3 Relative RI of targets

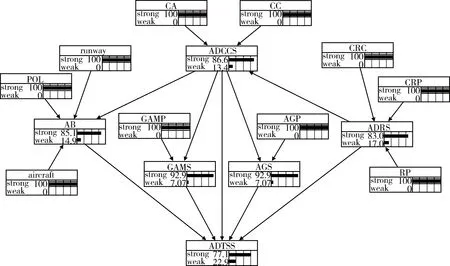
圖4 第1階段網(wǎng)絡(luò)更新結(jié)果Fig.4 First stage of network update result

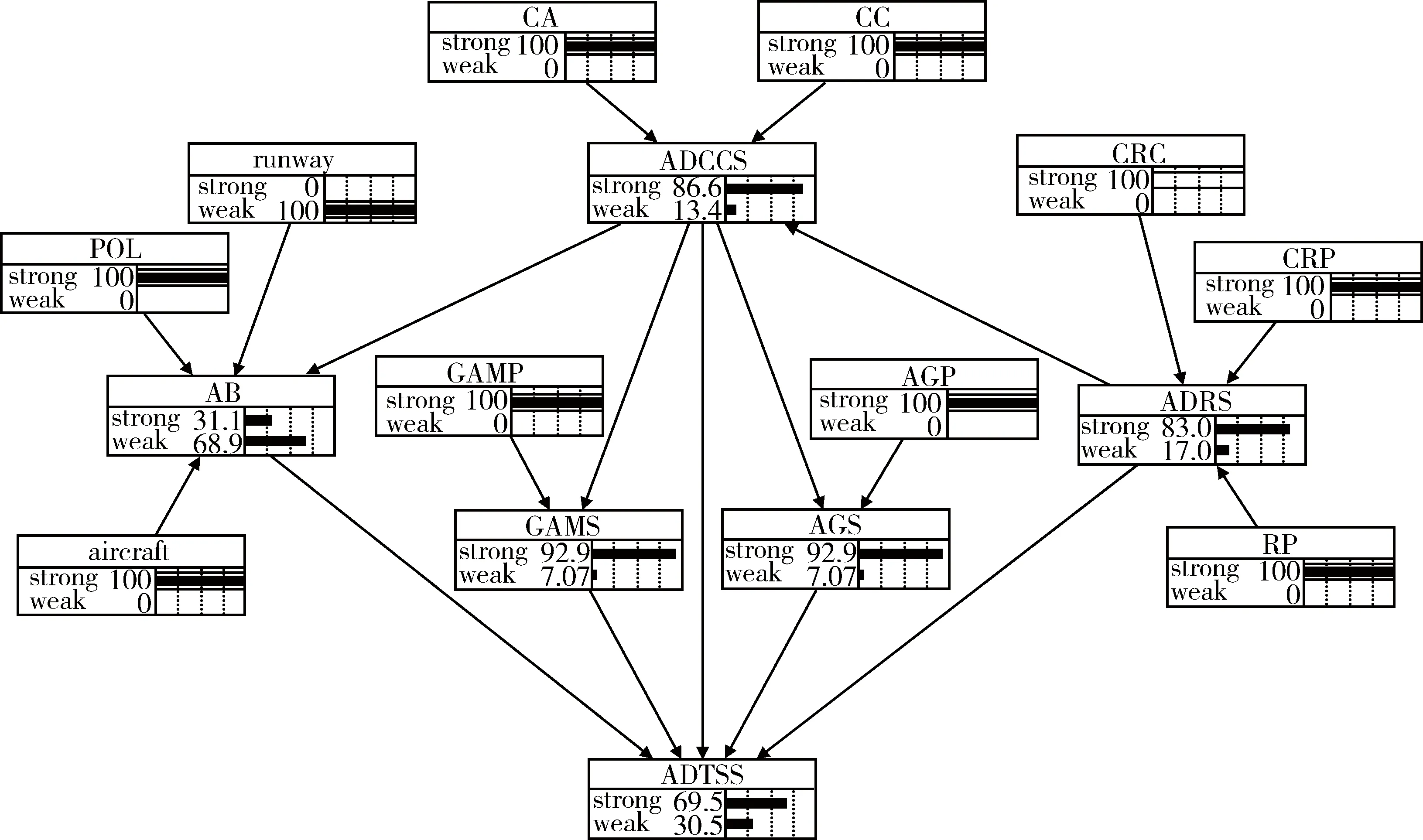
圖5 第2階段網(wǎng)絡(luò)更新結(jié)果Fig.5 Second stage of network update result

4 結(jié)束語

本文針對目標(biāo)體系構(gòu)造特點，采用貝葉斯網(wǎng)絡(luò)，建立了目標(biāo)選擇貝葉斯網(wǎng)絡(luò)模型，實現(xiàn)了對目標(biāo)體系內(nèi)各類型目標(biāo)初步的重要性分析。以目標(biāo)對體系的相對影響度為依據(jù)，對目標(biāo)進行排序，找出關(guān)鍵目標(biāo)，方便指揮機構(gòu)決策。該方法概念清晰，計算簡單，不但能夠集成專家的意見和知識，而且還具有強大的數(shù)據(jù)學(xué)習(xí)能力和推理能力，充分利用了所有可用信息。通過實例的仿真應(yīng)用，表明該方法能夠按照設(shè)計要求，較快地得出結(jié)果，驗證了模型的有效性和準確性。下一步，將結(jié)合各類型目標(biāo)的特征，對模型進行拓展和研究，實現(xiàn)對目標(biāo)體系的火力分配和毀傷效果評估。

參考文獻：

[1] 胡孝民，應(yīng)甫成. 聯(lián)合火力戰(zhàn)理論[M]. 北京：國防大學(xué)出版社，2003.

HU Xiao-min, YING Fu-cheng. Joint Fire Battle Theory[M]. Beijing: National Defense University Press,2003.

[2] 任富興，王雪琴. 聯(lián)合火力戰(zhàn)毀傷理論[M]. 北京：解放軍出版社，2010.

REN Fu-xing, WANG Xue-qin. Joint Fire Battle Damage Theory[M]. Beijing: PLA Press,2010.

[3] 馬志軍，賈希勝，陳麗. 基于貝葉斯網(wǎng)絡(luò)的目標(biāo)毀傷效果評估研究[J]. 兵工學(xué)報，2008,29(12)：1509-1513.

MA Zhi-jun, JIA Xi-sheng, CHEN Li. Battle Damage Assessment Based on Bayesian Network[J]. Acta Armamentarii, 2008,29(12):1509-1513.

[4] 雷霆，朱承. 目標(biāo)體系描述與火力分配方法研究[J]. 軍事運籌與系統(tǒng)工程，2012,26(1):67-72.

LEI Ting, ZHU Cheng. Research on the Description and Fire Distribution Method of Target System[J]. Military Operations Research and Systems Engineering, 2012,26(1):67-72.

[5] Pousi Jouni. Decision Analytical Approach to Effects-Based Operations[D].Helsinki: Helsinki University of Technology, 2009:35-63.

[6] 張國春，胡曉峰. 體系對抗仿真中體系效能分析初探[J]. 系統(tǒng)仿真學(xué)報，2003,15(12)：1698-1701.

ZHANG Guo-chun, HU Xiao-feng. The Initial Study of SoS Effectiveness Analysis in SoS Combat Simulation[J]. Journal of System Simulation, 2003,15(12)：1698-1701.

[7] 來淼，王躍利. 面向體系的目標(biāo)選擇形式化描述及分析[J]. 指揮控制與仿真，2007,29(5)：26-28.

LAI Miao,WANG Yue-li.Formalized Description and Analysis of Target Selection Model on System of System Oriented[J]. Command Control & Simulation, 2007,29(5)：26-28.

[8] 李望西，黃長強，吳文超，等. 空地精確制導(dǎo)武器對地攻擊目標(biāo)毀傷評估[J]. 系統(tǒng)工程理論與實踐，2012,32(1)：211-218.

LI Wang-xi, HUANG Chang-qiang, WU Wen-chao,et al. Battle Damage Assessment of Air-to-Ground Precision Guided Weapon Air-to-Ground Attack[J]. Systems Engineering Theory & Practice, 2012,32(1)：211-218.

[9] David Heckerman. A Tutorial on Learning with Bayesian Networks[R]. Redmond: Microsoft Corporation, 1995.

[10] Lucia Falzon. Using Bayesian Network Analysis to Support Centre of Gravity Analysis in Military Planning[J]. European Journal of Operational Research, 2006,170(9):629-643.

[11] Joint and National Intelligence Support to Military Operations[R]. Joint Staff, 2004.

[12] Joint Intelligence[R]. Joint Staff, 2007.