助推-滑翔飛行器彈道最優控制研究*

范文鋒，許波，郝昀

(北京機電工程總體設計部，北京 100854)

0 引言

近年來，隨著臨近空間的利用逐漸受到重視，一種助推-滑翔式飛行器(boost-glide vehicle, BGV)得到國內外學者廣泛關注[1-6]。其特點是通過主動段的快速助推使飛行器達到較大速度和高度，隨后在臨近空間以無動力跳躍滑行的方式進行長時間機動飛行，具有可實現遠程快速精確攻擊、覆蓋區域大、機動性能好及突防能力較強等優點。本文擬對助推-滑翔飛行器彈道最優控制問題進行研究。

目前求解此類彈道優化問題主要有間接法和直接法兩大類[7]。間接法是根據Pontryagin極小值原理將約束最優控制問題轉化為Hamiltonian邊值問題(Hamiltonian boundary value problem, HBVP)進行求解，其特點是解的精度較高且滿足一階最優性必要條件，然而收斂半徑小且協態變量初值難以給定等問題成為此類方法廣泛應用的主要困難。直接法采用參數化方法將連續空間的最優控制問題離散轉化為非線性規劃(non-linear programming, NLP)問題，進而使用成熟的NLP求解方法得到最優彈道，由于直接法不必推導一階最優必要條件，收斂半徑大，無需協態變量的初始值，因此直接法比間接法應用更為廣泛。

本文以助推-滑翔飛行器為研究對象，建立無量綱化的彈道動力學模型并提煉出總體設計參數，考慮飛行中的實際約束，以射程最優為目標建立BGV彈道最優控制模型；采用Radau偽譜方法將約束最優控制問題轉化為非線性規劃問題，通過引入連接點概念處理多階段不連續問題，并使用序列二次規劃方法(sequential quadratic programming, SQP)進行求解；最后給出數值優化算例，說明彈道最優控制設計特點以及文中方法的實用性和有效性。

1 彈道動力學模型

1.1 基本假設

本文以助推-滑翔飛行器為研究對象，僅限于均勻重力場中的縱向飛行彈道，考慮地球形狀，忽略地球自轉及扁率的影響。

1.2 氣動力模型

借鑒文獻[8]中擬合得到的高精度氣動模型，其結果如下：

CD=0.000 68Ma4-0.014 1Ma3+0.110 21Ma2-

0.408 38Ma+0.822 73α+0.174 92，

(1)

CL=2.423 9×10-6Ma5-1.895×10-5Ma4+

1.863 910-5Ma3-0.000 48Ma2+0.003 94Ma-

0.000 93α2+α+69.656.

(2)

1.3 大氣密度模型

假設大氣密度遵循指數變化規律，其表達式為

ρ=ρ0exp-βH,

(3)

式中：ρ0為海平面大氣密度，1.225 kg/m3；β=1/7 200。

1.4 無量綱化動力學模型

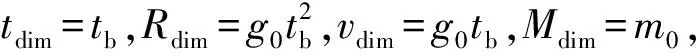
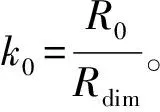
當發動機工作結束后開始被動段飛行，此時僅考慮動力學方程組中前4項即為被動段動力學方程組。

綜上可知：助推-滑翔飛行器的主要設計參數可歸納為tb，μt，Kfg，Kgs，CD和CL，由于tb=Ispμt/Kfg，因此最大射程可表示為

Lmax=fIsp,μt,Kfg,Kgs,CD,CL.

(5)

2 彈道最優控制模型

2.1 約束條件

助推-滑翔飛行器飛行彈道經歷嚴酷的力、熱環境，需要考慮氣動加熱、結構承載以及姿態穩定的需求，提出如下過程約束以確保飛行正常。

駐點熱流密度約束：

(6)

總過載約束：

(7)

動壓約束：

(8)

此外，為保證對目標的打擊效果，對落點狀態提出如下終端約束：

Θtf=Θf,

(9)

(10)

2.2 BGV彈道最優控制問題

在以上工作基礎上，本文研究的助推-滑翔飛行器彈道最優控制問題可以描述為求解飛行攻角α，使得如下目標函數最大：

(11)

且滿足狀態方程組(4)、過程約束(6)～(8)以及終端約束(9)～(10)。

3 Radau偽譜方法

偽譜法也稱正交配點法，主要包括Legendre偽譜法(Legendre pseudo-spectral method, LPM)、Gauss偽譜法(Gauss pseudo-spectral method, GPM)以及Radau偽譜法(Radau pseudo-spectral method, RPM)。這些方法相同之處都采用Lagrange多項式對狀態變量和控制變量進行全局逼近，區別在于配點的選取不同。文獻[9]對以上3種偽譜方法特點進行了詳細討論，指出采用GPM 和RPM得到的NLP問題KKT(Karush-Kuhn-tucker)條件與原HBVP一階最優性必要條件等價。由于RPM配點包含初始點，容易得到協態變量高精度初始值，本文采用RPM對助推-滑翔飛行器彈道最優控制問題進行求解。

3.1 基本原理

Radau偽譜法將約束最優控制問題的狀態變量和控制變量在Legendre-Gauss-Radau(LGR)配點處進行離散，采用全局插值的Lagrange多項式對狀態變量和控制變量進行全局逼近，通過對多項式求導來近似狀態方程中的導數，且在一系列配點上滿足控制方程中右函數的約束，從而將狀態方程轉化為代數形式的等式約束；目標函數中的積分項由Gauss-Radau積分近似計算；至此可將約束最優控制問題轉化為非線性規劃問題[10]。

3.2 連續最優控制問題的離散轉換

3.2.1 連續最優控制問題的一般格式

不失一般性，考慮如下Bolza最優控制問題。求解控制函數ut及相應的狀態函數xt，使得如下目標函數最小：

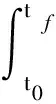
(12)

滿足狀態方程：

(13)

過程約束：

gxt,ut,t≤0，

(14)

邊界約束：

ψxt0,t0,xtf,tf=0.

(15)

3.2.2 離散轉換的主要內容

(1) 時域轉換

Radau偽譜法的求解時域為 [-1,1]，因此需要將實際求解時域[t0,tf]進行轉化：

(16)

(2) 狀態變量與控制變量的近似

Radau偽譜法采用全局正交的Lagrange插值多項式分別對狀態變量與控制變量進行逼近。

狀態變量的近似公式為

(17)

(18)

式中：τjj=1,…,N為LGR配點，對應LN-1τ+LNτ的根，LNτ表示N階Legendre多項式；τN+1不屬于LGR配點但參與狀態變量離散近似過程，其取值為1。

控制變量只在LGR配點處進行離散近似，其近似公式為

(19)

(20)

(3) 狀態方程轉換

將式(17)對τ進行微分，可得到LGR配點處的狀態變量導數為

(21)

式中：Dkj為N×N+1階Radau偽譜微分矩陣分量。

(22)

在此基礎上，可將LGR配點處狀態方程轉化為代數形式的等式約束：

k=1,2，…,N.

(23)

(4) 積分項的近似

最優控制問題中的積分項采用Gauss-Radau積分進行處理。不失一般性，其轉換格式為

(24)

式中：ωk為Gauss-Radau積分權重。

3.2.3 轉換后的非線性規劃問題

基于以上離散處理可將最優控制問題式(12)～(15)轉換為如下形式：

J=HxNτ1,τ1,xNτN+1,τN+1+

(25)

滿足約束：

k=1,2，…,N.

顯然式(25)，(26)構成一個非線性規劃問題，即求解離散點處的狀態變量xNτk(k=1,2，…,N+1)、LGR配點處的控制變量uNτk(k=1,2，…,N)以及終端時刻tf(若未給定)，使式(25)在滿足式(26)的約束下最小，可采用成熟的SQP方法求解。

3.3 多階段不連續問題處理

對于助推-滑翔飛行器，主動段及被動段動力學模型存在差別，其彈道優化本質上是一個多階段不連續最優控制問題。通過引入連接點的概念形成多階段偽譜方法[11-12]，即根據不同階段動力學模型及約束條件變化特點將最優控制問題劃分成若干子區間，在每個子區間上分別對狀態變量和控制變量進行離散配點，同時對相鄰子區間連接點加入約束條件，以處理多階段不連續的最優控制問題。

假設在某一點τ1∈[τ0,τ2]存在不連續，記

則連接點約束條件為

φ(x-(τ1),x+(τ1))≤0.

(27)

當τ1為不定時，可將其作為優化變量，同時加入不等式約束條件：

τ1-τ0τ1-τ2≤0.

(28)

4 數值優化算例

優化過程中根據計算精度需求及彈道特點選取配點數，其中主動助推段LGR配點數取75個，被動滑翔段LGR配點數取105個。總體設計參數取值如表1所示，過程約束及終端約束指標如表2所示。以助推-滑翔飛行器總射程最大為目標進行優化，結果如圖1～7所示。

表1 總體設計參數值Table 1 Parameters for overall design

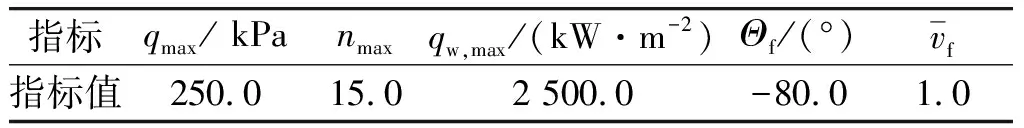
表2 約束指標Table 2 Specifications for constraints

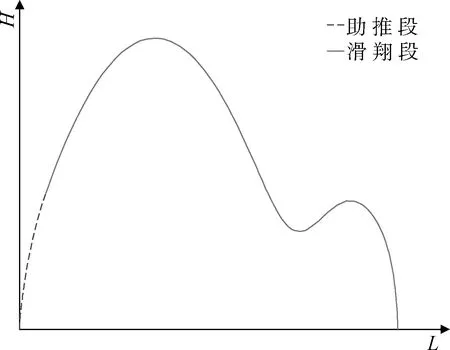
圖1 縱向平面彈道Fig.1 Planar trajectory

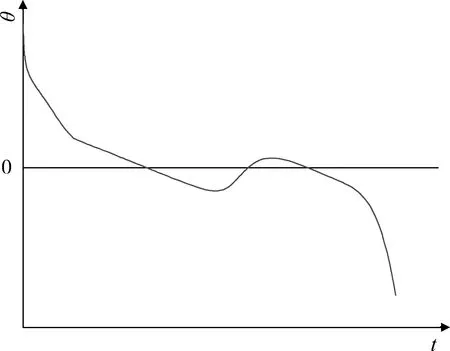
圖2 當地彈道傾角Fig.2 Flight path angle

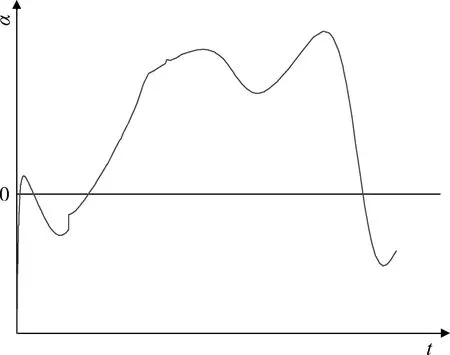
圖3 飛行攻角Fig.3 Angle of attack

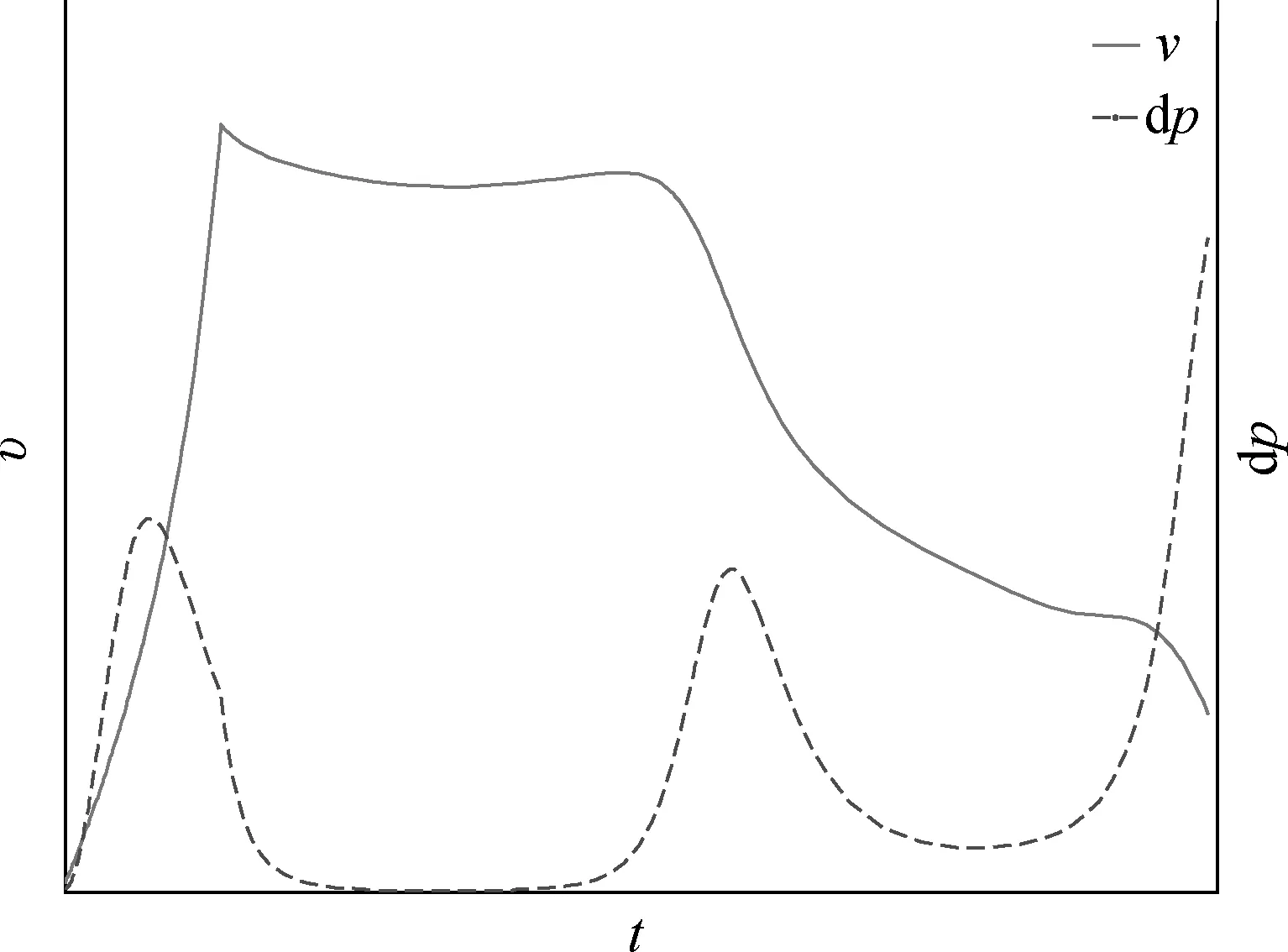
圖4 總速度與動壓Fig.4 Total velocity and dynamic pressure

優化結果表明：各狀態及控制變量曲線過渡光滑，且滿足過程及終端約束。由圖3飛行攻角曲線可知：采用2次攻角轉彎的策略進行主動段飛行程序設計，有利于精細調節主動段能量損失；被動滑翔段采用波浪式攻角變化規律，而非采用最大升阻比狀態定常攻角飛行策略，更有利于提高射程。

由圖6可知與飛行距離相關的協態變量值恒為-1，由圖7可知Hamiltonian函數在主動助推段和被動滑翔段均保持為常值，基于助推-滑翔飛行器彈道最優控制模型特點，可知圖6～7結果從側面說明了采用的多階段Radau偽譜方法得到的KKT條件與原HBVP一階最優性必要條件等價，計算結果與理論最優解一致。

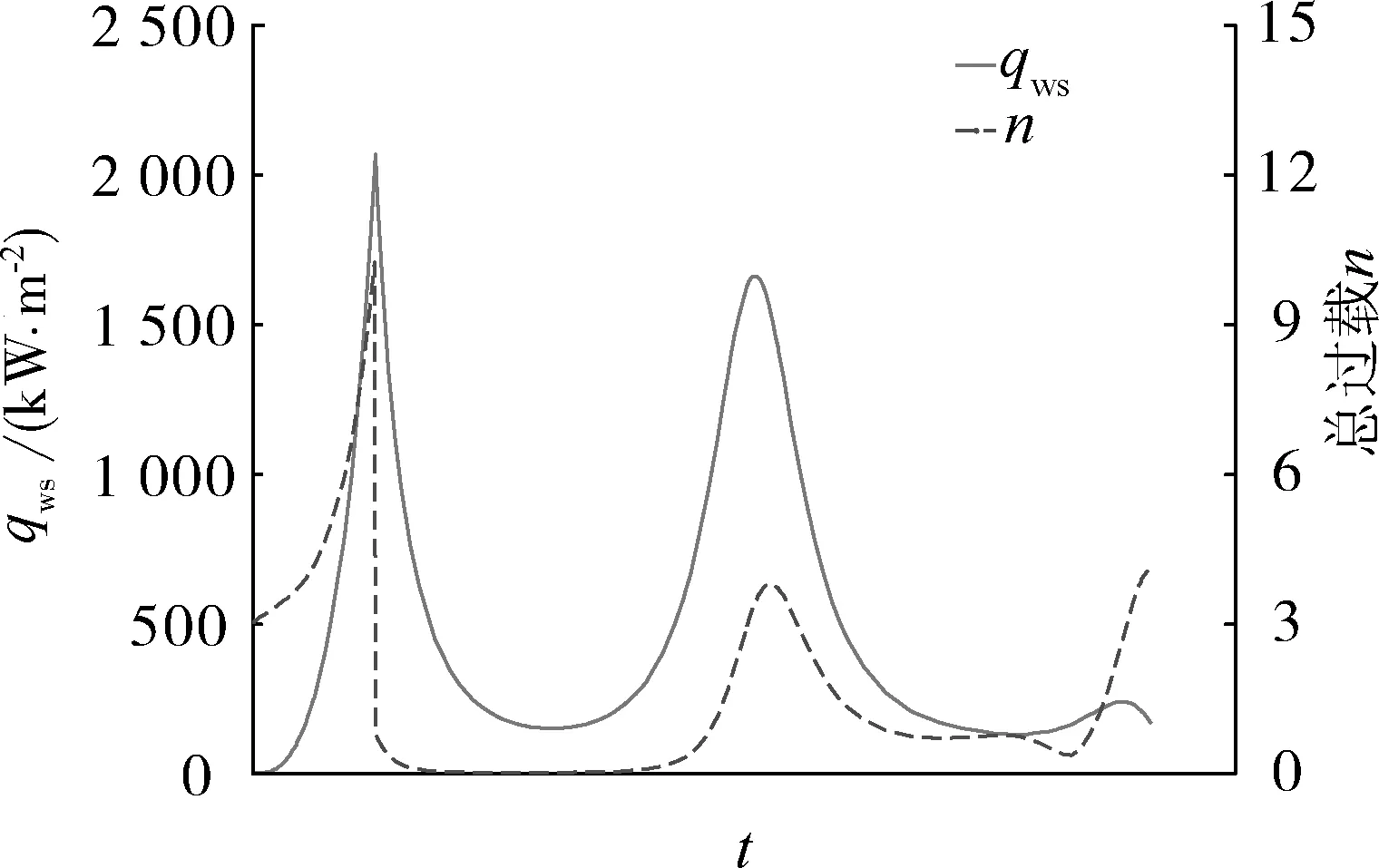
圖5 駐點熱流密度與總過載Fig.5 Heat flux at the stagnation point and total overload

圖6 飛行距離相關的協態變量Fig.6 Co-state about flight range

圖7 哈密頓函數Fig.7 Time history for Hamiltonian

5 結論

本文從多階段多約束最優控制的角度對助推-滑翔飛行器彈道最優控制問題進行研究，得到結論如下：

(1) 通過無量綱化方法得到助推-滑翔飛行器無量綱化動力學方程組，可提取出Isp，μt，Kfg，Kgs，CD和CL作為BGV總體設計的主要參數。

(2) 建立了助推-滑翔飛行器彈道最優控制模型，采用Radau偽譜方法將最優控制問題轉化為NLP問題并使用SQP方法求解；通過數值優化算例驗證了模型及方法實用有效，優化結果滿足一階最優性必要條件。

(3) 助推-滑翔飛行器彈道包括主動助推段和被動滑翔段2部分，其彈道優化是典型的多階段不連續最優控制問題；通過引入連接點的概念處理多階段不連續問題，可避免以往彈道分段優化的缺陷，以全射程最優直接處理助推-滑翔飛行器彈道最優控制問題。

參考文獻：

[1] 劉欣, 楊濤, 張青斌. 助推-滑翔導彈彈道優化與總體參數分析[J].彈道學報, 2012, 24(3): 43-48.

LIU Xin, YANG Tao, ZHANG Qing-bin. Trajectory Optimization and Parameter Analysis for Boost-Glide Missile[J]. Journal of Ballistics, 2012, 24(3): 43-48.

[2] 李瑜, 楊志紅, 崔乃剛. 助推-滑翔導彈最大射程優化[J]. 彈道學報, 2008, 20(4): 53-56.

LI Yu, YANG Zhi-hong, CUI Nai-gang. Optimization of Maximum Range for Boost-Glide Missile[J]. Journal of Ballistics, 2008, 20(4): 53-56.

[3] 李珂, 聶萬勝, 馮必鳴. 助推-滑翔飛行器彈道分段研究[J]. 指揮控制與仿真, 2012, 34(5): 21-25.

LI Ke, NIE Wan-sheng, FENG Bi-ming. Research on Multi-phase Trajectory Optimization for Boost-Glide Vehicle[J]. Command Control & Simulation, 2012, 34(5): 21-25.

[4] 劉欣, 楊濤. 滑翔導彈再入拉起段彈道優化與制導[J].國防科技大學學報, 2012, 34(1): 67-71.

LIU Xin, YANG Tao. Trajectory Optimization and Guidance in Reentry Phase for Glide Missile[J]. Journal of National University of Defense Technoloty, 2012, 34(1): 67-71.

[5] 王晨曦, 李新國. 助推-滑翔導彈射程管理技術研究[J]. 固體火箭技術, 35(2): 143-147.

WANG Chen-xi, LI Xin-guo.Range Management Technology Research of Boost Glide Missiles[J]. Journal of Solid Rocket Technology, 35(2): 143-147.

[6] 劉君, 陳克俊, 謝愈, 等. 助推滑翔飛行器發射諸元計算方法研究[J]. 彈箭與制導學報, 2012, 32(6): 33-36.

LIU Jun, CHEN Ke-jun, XIE Yu, et al. The Research on Computing Method for Firing Data of Boost-Glide Aerocraft[J]. Journal of Projectiles, Rocket, Missiles and Guidance, 2012, 32(6): 33-36.

[7] 楊秀霞, 張毅, 施建洪, 等. 助推-滑翔飛行器軌跡設計研究綜述[J]. 海軍航空工程學院學報, 2012, 27(3): 245-252.

YANG Xiu-xia, ZHANG Yi, SHI Jian-hong, et al. A Survey of Boost-Glide Aircraft Trajectory Design[J]. Journal of Naval Aeronautical and Astronautical University, 2012, 27(3): 245-252.

[8] 宗群, 田柏苓, 竇立謙. 基于Gauss偽譜法的臨近空間飛行器上升段軌跡優化[J]. 宇航學報, 2010, 31(7): 1775-1781.

ZONG Qun, TIAN Bai-ling, DOU Li-qian. Ascent Phase Trajectory Optimization for Near Space Vehicle Based on Gauss Pseudo-Spectral Method[J]. Journal of Astronautics，2010, 31(7): 1775-1781.

[9] Divya Garg. Advances in Global Pseudo-Spectral Methods for Optimal Control [D].Gainesville,USA: University of Florida, 2011.

[10] HAN Peng, SHAN Jia-yuan, MENG Xiu-yun. Reentry Trajectory Optimization Using a Multiple-Interval Radau Pseudo-Spectral Method[J]. Journal of Beijing Institute of Technology, 2013, 22(1): 20-27.

[11] 楊希祥, 張為華. 基于Gauss偽譜法的固體火箭上升段軌跡快速優化研究[J]. 宇航學報, 2011, 32(1): 15-21.

YANG Xi-xiang, ZHANG Wei-hua. Rapid Optimization of Ascent Trajectory for Solid Launch Vehicles Based on Gauss Pseudo-Spectral Method[J]. Journal of Astronautics,2011, 32(1):15-21.

[12] 關成啟, 陳聰. 基于Gauss偽譜法的助推-滑翔飛行器多階段約束軌跡優化[J]. 宇航學報, 2010,31(11): 2512-2518.

GUAN Cheng-qi, CHEN Cong. Multiphase Path-Constrained Trajectory Optimization for the Boost-Glide Vehicle Via the Gauss Pseudo-Spectral Method[J]. Journal of Astronautics， 2010, 31(11): 2512-2518.