沖壓發動機導彈軌跡/總體參數一體化優化設計*

沙建科，施雨陽，萬自明，徐敏

(1.西北工業大學 航天學院，陜西 西安 710072； 2.北京電子工程總體研究所，北京 100854)

0 引言

沖壓發動機以質量輕、比沖高、具有良好的超聲速特性而成為中遠程戰術導彈首選裝置，其可為導彈超聲速飛行提供加速爬升所需要的富裕推力及續航推力[1]。以沖壓發動機為動力的導彈武器系統研制工作是一項系統工程，總體設計決定導彈的性能和成本。優化設計是從多種方案中選擇最佳方案的設計方案，是導彈總體設計的一個重要手段。導彈總體優化設計的重要任務之一是對導彈設計參數進行尋優，使導彈以最小代價滿足戰術技術指標的要求[2]。

隨著優化理論的不斷完善，分系統優化設計方法如導彈總體參數和彈道優化設計已經很成熟[3-7]。沖壓發動機的性能參數(如比沖、推力)與導彈飛行參數緊密相關，而導彈的飛行性能與給定的彈道形狀有關，各分系統單獨開展的優化設計并不能滿足總體參數最優的要求，要想獲得總體參數優化最優必須結合飛行軌跡進行一體化優化設計。總體參數/飛行軌跡一體化優化才能使系統參數最優，從而最大程度地挖掘導彈的設計潛能。

本文從一體化優化設計思想出發，對以沖壓發動機為動力導彈軌跡/總體參數一體化設計中的相關數學模型、優化目標、一體化優化方法等幾個問題進行了深入研究。提出了采用一種精度高的參數化方法-高斯偽譜法將軌跡最優控制問題轉換為非線性規劃問題，然后用序列二次規劃方法(sequential quadratic programming, SQP)求解一體化優化問題。

1 導彈總體優化數學模型

數學模型包括質量計算模型、彈道及氣動力計算模型和發動機性能計算模型。

1.1 導彈質量計算模型

導彈的質量計算是軌跡/總體參數一體化優化設計基礎，導彈總質量由各部分質量組成。在導彈總體方案論證階段宜采用導出型質量計算模型。本文的質量計算按照部件分析方法進行估算，全彈質量M0由助推器質量M1和二級導彈質量M2組成：

M0=M1+M2.

(1)

助推器采用固體火箭發動機，為了簡化模型，認為助推器質量由推進劑Mp和結構質量Ms組成。依據有關統計數據，發動機推進劑質量為

Ms=0.85M1.

(2)

二級導彈的質量可分為有效載荷質量mp、發動機推進劑質量mpp、發動機結構質量mss1、能源電池質量mcs、導彈結構質量mss和彈上設備質量mps。即

M2=mp+mpp+mss1+mcs+mss+mps.

(3)

各部分質量具體展開表達式可參考文獻[2].

1.2 發動機性能計算模型

總體參數優化建模中必須根據實際要求建立發動機性能的計算模型。發動機為導彈提供飛行動力，以保證導彈獲得所需的速度和射程。沖壓發動機最大的缺點是在靜止狀態下不能自行啟動，必須借助助推器將其加速到一定的速度后才能工作。因此，本文的動力系統由助推器(固體火箭發動機)和沖壓發動機組成。

為了簡化計算，在總體方案設計階段，認為固體火箭發動機的推力為定值，燃料流率為一確定值。采用等熵流動，一維計算模型對沖壓發動機進行熱力計算，具體可見文獻[8]。通過仿真得到沖發動機的推力、耗油量隨飛行高度、速度、攻角、沖壓發動機余氣系數、喉道收縮比的變化關系，即

F=f1(h,v,α,β,η)，

(4)

mc=f2(h,v,α,β,η)，

(5)

式中：F為推力；mc為耗油量；h為飛行高度；v為飛行速度；α為飛行攻角；β為余氣系數；η為喉道收縮比。

1.3 彈道計算模型

導彈的彈道由起飛助推段、爬升段和巡航段組成。助推器在地面點火加速到沖壓發動機啟動馬赫數以后脫落，沖壓發動機開始接力工作使導彈加速爬升到巡航高度、巡航速度后進行水平巡航。為了研究方便，采用了以下假設：①將導彈看作可控質點；②為簡化問題，僅研究導彈在垂直平面內的運動；③略去飛行過程中的隨機干擾，即控制系統是理想的，導彈運動完全按照程序飛行。

基于以上假設，導彈在鉛垂平面內的質心運動方程組為

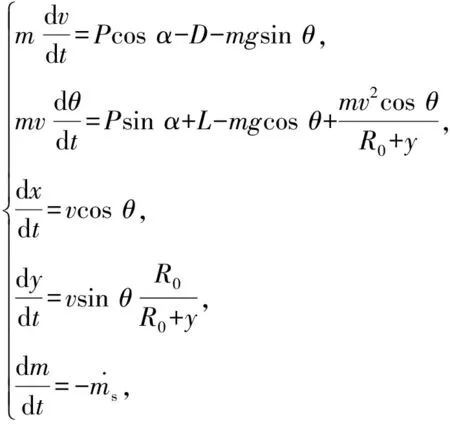
(6)

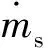
大氣模型采用1976美國標準大氣。導彈的氣動力計算采用部件組合的工程估算方法，基本能滿足導彈總體方案設計的精度要求。阻力D和升力L分別為

(7)

(8)

式中：S為參考面積；ρ為大氣密度；CD和CL分別為阻力系數和升力系數，可表示為攻角和馬赫數的插值函數，也可近似表示為攻角的函數。

2 導彈軌跡/總體一體化優化問題描述

2.1 目標函數

優化設計的任務就是要對各個設計方案進行尋優比較，得出最佳方案，而對設計方案進行優劣比較的準則就是目標函數。目標函數應能充分反映主要設計性能指標。本文以起飛質量最小為目標函數，該目標函數既能反映了導彈性能的好壞，也在一定程度上反映了成本。

2.2 優化變量

優化設計變量是指能夠用來描述設計方案特征的獨立變量。優化變量應選取與目標函數有關系，對目標有較大影響的變量。本文的優化變量由總體參數優化和軌跡優化兩者的優化變量組成。根據問題性質和設計經驗，選取下述的優化變量。

(1) 助推器工作時間t1

在裝藥量一定時，助推器工作時間越短，助推段末速就越大，但相應的導彈結構質量也增加，且受到發動機燃燒室壓強的限制，發動機工作時間也不可能無限制的縮短，因此，需通過優化助推工作時間以提高導彈總體性能。

(2) 初始彈道傾角θ0

增大初始彈道傾角可使導彈快速爬升到預定的巡航高度，減少阻力的消耗，增加巡航射程，但是也增加了爬升段重力的消耗，同時減少了水平飛行距離，為了提高總體性能應優化初始彈道傾角。

(3) 接力馬赫數Mat1f

接力馬赫數為助推段的末速，二級導彈的初速，是導彈總體設計指標。接力馬赫數值增大時，則助推段質量增加，反之，二級導彈的質量增加，導彈的起飛質量M0會因Mat1f的不同而發生變化。優化接力馬赫數可以使得導彈總體性能得到進一步的優化。

(4) 沖壓發動機余氣系數β及喉道收縮比η

發動機的性能參數取決于余氣系數及喉道收縮比，因此β和η影響著導彈的飛行性能，為達到給定的射程，總可能找到合適的β和η使得導彈的起飛質量最小。

(5) 軌跡最優攻角變化規律α(t)

飛行攻角是軌跡的控制變量，優化飛行攻角使得軌跡最優減少燃油消耗，從而達到起飛質量最小的目的。

2.3 約束條件

導彈在飛行過程中經歷助推段、爬升段和巡航段，跨越的時間和空間范圍比較大。飛行過程中受到過程不等式約束、終端約束。此外，相鄰的2段軌跡(助推段與爬升段、爬升段與巡航段)之間還需要滿足結點連接條件。本文的約束條件如下：

不等式約束：

αmin≤αmax，Mat1f>Ma0，

(9)

等式約束：

hti3=hcruise，θti3=θcruise，vti3=vcruise，L=Lmax.

(10)

相鄰兩段連接約束：

(11)

式中：Mat1f為沖壓發動機機轉級馬赫數；tf1為助推段關機時刻，為固定值；ti2和tf2分別為爬升段初始時刻和終端時刻；ti3為巡航初始時間。

爬升段轉到巡航段的標志是爬升段彈道傾角為0。

2.4 一體化優化方法

導彈軌跡/總體參數一體化優化變量分為2類，一類是導彈總體參數靜態優化；另一類是動態軌跡優化。由以上分析可知，總體參數優化問題屬于非線性規劃問題，而軌跡優化設計本質上屬于最優控制問題。采用基于pontryagin極小值原理的間接求解軌跡優化問題比較繁瑣，且只能與總體參數優化分開單獨優化，有可能失去整體的最優解，本文利用基于非線性規劃的直接法來求解。軌跡最優控制問題的搜索空間是泛函空間，不能直接利用非線性規劃算法進行求解。為了統一用非線性規劃算法求解軌跡/總體一體化優化問題，應該用參數化方法將軌跡最優控制問題轉化為非線性規劃問題。參數化方法是將最優軌跡問題轉化為非線性規劃問題求解的橋梁，其精度直接關系到最優軌跡的好壞程度。本文提出采用高斯偽譜法將軌跡最優控制問題轉化為非線性規劃問題。

高斯偽譜法是近年來發展迅速、應用較多的一種同時離散控制變量和狀態變量的函數逼近參數化方法[9-11]。高斯偽譜法屬于配點法的范疇，其基本原理是：以Legendre多項式的零點(也稱為高斯點)作為節點同時將狀態方程中的控制變量和狀態變量進行離散，然后以這些節點作為插值點構造全局的拉格朗日多項式來逼近狀態變量及控制變量，通過對全局插值多項求導來近似動力學方程中的狀態變量對時間的導數，從而將動力學方程轉化為一組代數方程。目標函數中的積分項由高斯積分計算得到。經過上述變換，可將軌跡最優控制問題轉化為受一系列代數約束的參數優化問題，即非線性規劃問題，基本流程圖如圖1所示。

高斯偽譜法的優點主要表現在：①可估算出原最優控制問題的協態變量信息，因此能保證所獲得的非線性規劃的最優解是原最優控制問題的解。②因同時離散控制變量及狀態變量，其優化變量的維數遠高于其他方法，但以此為代價，降低了目標函數的病態方程，提高了收斂性和精度，且對初值猜測值不敏感。

高斯偽譜方法將軌跡最優控制問題參數化，轉化為非線性規劃問題后， 理論上各種非線性規劃算法均適用該問題求解。本文提出采用SQP算法對該問題進行求解。SQP優化算法[12]是在每一迭代步中，通過求解一個二次規劃子問題，來確定一個下降方向，以減少價值函數來取得步長，重復這些步驟，直到求得原問題的解，該方法在局部整體收斂性的同時，保持局部超1次收斂性，是求解約束優化問題最有效的算法之一，也是應用最為成功和廣泛的一種算法。

3 仿真結果與討論

根據本文所建立的軌跡/總體一體化優化方法，以某遠程沖壓發動機導彈為例，分別對不考慮軌跡優化的總體參數優化(總體優化方案)和考慮軌跡/總體參數一體化優化(一體化優化方案)進行了仿真分析。本算例的初值為：(h,x,v)=(0,0,0)；約束為Mat1f>1.8，α(t)∈[-3°,8°]，t1∈[3,7]。計算中巡航高度為16 km，巡航馬赫數為3，射程為300 km。優化結果如表1所示。

圖1 高斯偽譜法基本流程圖Fig.1 Basic block diagram of Gauss pseudo-spectral method

表1 總體參數優化結果Table 1 Overall parameter optimization results

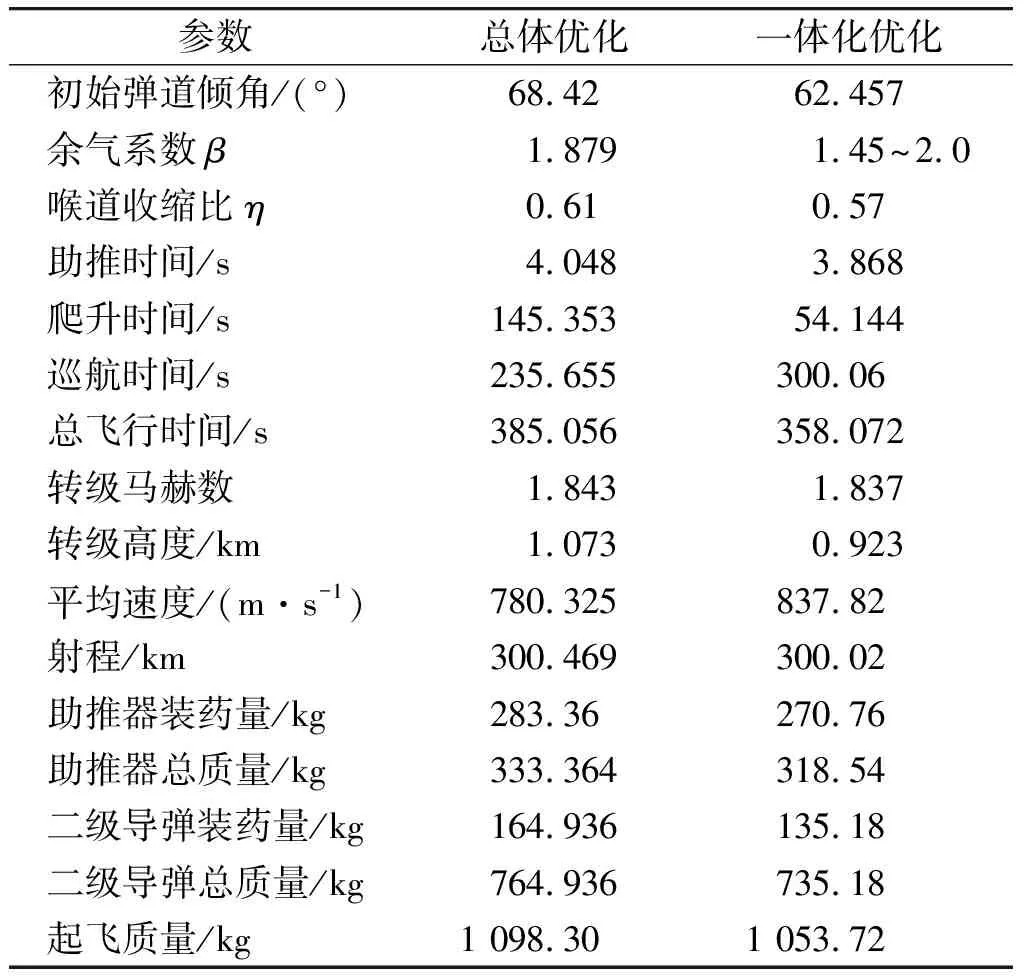
參數總體優化一體化優化初始彈道傾角/(°)68.4262.457余氣系數β1.8791.45～2.0喉道收縮比η0.610.57助推時間/s4.0483.868爬升時間/s145.35354.144巡航時間/s235.655300.06總飛行時間/s385.056358.072轉級馬赫數1.8431.837轉級高度/km1.0730.923平均速度/(m·s-1)780.325837.82射程/km300.469300.02助推器裝藥量/kg283.36270.76助推器總質量/kg333.364318.54二級導彈裝藥量/kg164.936135.18二級導彈總質量/kg764.936735.18起飛質量/kg1 098.301 053.72

從上述優化結果可以看出，在沖壓發動機接力工作時，2種方案的導彈飛行馬赫數分別為1.834和1.837，均滿足接力馬赫數的條件。接力馬赫數的大小，主要取決于助推器和二級發動機的比沖，沖壓發動機的比沖遠遠大于固體火箭發動機的比沖，因此為了使起飛質量最小，接力馬赫數取值在沖壓發動機能正常工作附近。導彈起飛質量減少了4.06%，主要是助推段和爬升段燃油減少的結果，在總體參數優化中，增加軌跡的優化可以大大提高導彈的設計潛力。彈道曲線和速度隨時間變化曲線如圖2和圖3所示，一體化優化方案中，為了減少助推段重力的損失，助推器工作時間減小到3.818 s；導彈以較大的推力迅速爬升到巡航高度，在爬升轉平飛時，馬赫數為2.95，迅速爬升到預定高度，可減少阻力消耗，增加巡航段射程，充分發揮沖壓發動優勢。隨著飛行高度的增加，空氣密度減少，進入進氣道的空氣流量減小，使得燃料秒流量減少，從而達到了減輕起飛質量的目的。飛行攻角隨時間的變化如圖4所示，滿足約束要求，變化比較平滑，容易控制。

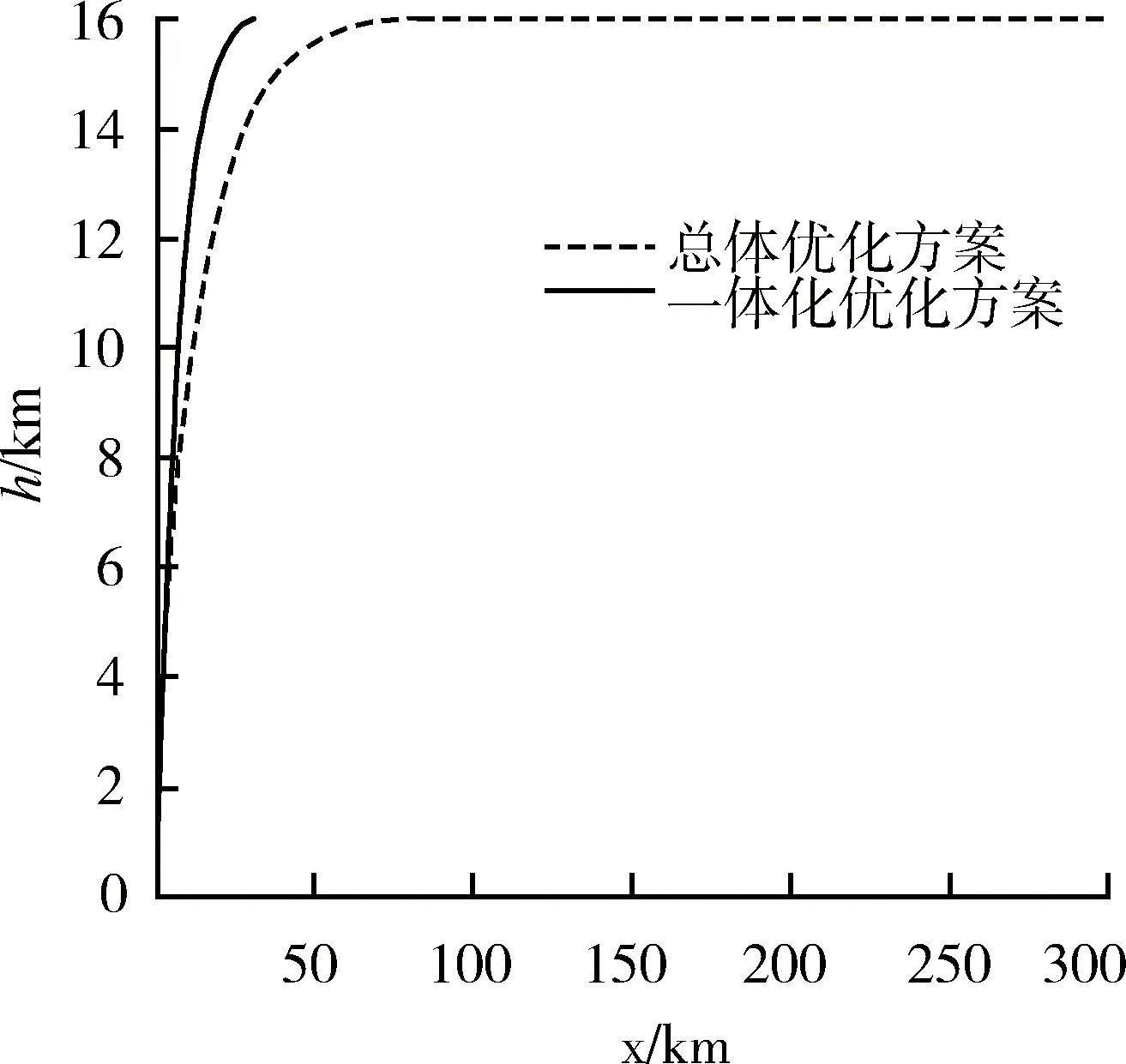
圖2 導彈彈道曲線Fig.2 Change curve of trajectory vs. time

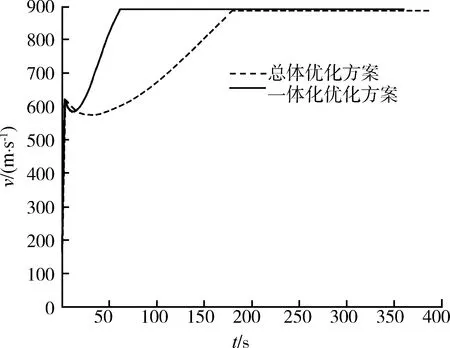
圖3 導彈飛行速度時間曲線Fig.3 Change curve of velocity vs. time

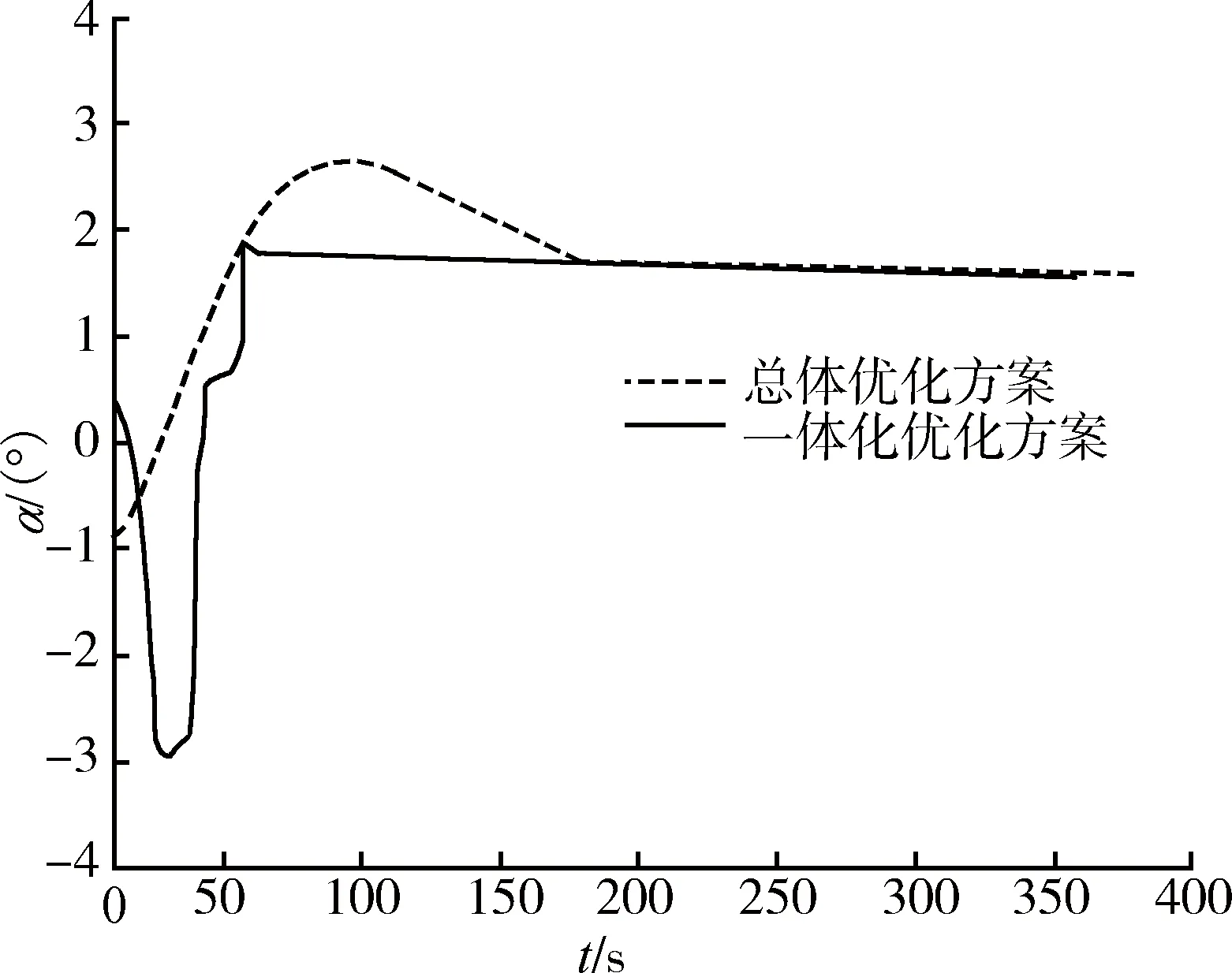
圖4 導彈飛行攻角時間曲線Fig.4 Attack angle curve of vs. time

4 結束語

本文針對沖壓發動機導彈的特點，建立了導彈軌跡/總體參數一體化優化設計模型及方法。為了用非線性規劃方法求解一體化優化問題，提出了采用高斯偽譜法將一體化中的軌跡最優控制問題轉化為非線性規劃問題。分別對軌跡/總體參數一體化優化和未考慮軌跡優化2種方案進行了仿真分析。仿真結果表明，起飛質量減少了4.06%，采用一體化優化設計思想，可以最大程度地挖掘導彈總體設計的潛力，其結果可為沖壓發動機導彈總體優化設計研究提供理論參考。

參考文獻：

[1] 鮑福廷，黃熙君, 張振鵬. 固體火箭沖壓組合發動機[M]. 北京：中國宇航出版社，2006.

BAO Fu-ting, HUANG Xi-jun, ZHANG Zhen-peng. Integral Solid Propellant Ramjet Rocket Motor [M].Beijing: China Astronautic Publishing House, 2004.

[2] 谷良賢，溫炳恒.導彈總體設計原理[M],西安：西北工業大學出版社，2004.

GU Liang-xian, WEN Bing-heng. Missile Overall Design Principle [M].Xi’an: NWPU Publishing House, 2004.

[3] 張弫，鄭時鏡，于本水. 遺傳算法在遠程防空導彈總體優化設計中的應用[J].系統工程與電子技術,2003,25(1):34-37.

ZHANG Zhen, ZHENG Shi-jing, YU Ben-shui. Application of the Genetic Algorithms in the Optimization Design of the Long-Range Air-Defense Missile System [J].Systems Engineering and Electronics,2003, 25(1):34-37.

[4] 李向林，于本水.GA與ST在防空導彈總體參數優化設計中的應用[J].系統工程與電子技術，2000,22(10):14-16.

LI Xiang-lin, YU Ben-shui. Application of Genetic Algorithm and Stepwise Tolerance Method in the Optimal Design of Systemic Parameter of Antiaircraft Missile [J]. Systems Engineering and Electronics, 2000, 22(10):14-16.

[5] 張弫，鄭時鏡，于本水.遠程防空導彈彈道設計技術研究[J]. 系統工程與電子技術，2003,25(3):304-307.

ZHANG Zhen, ZHENG Shi-jing,YU Ben-shui.Study on the Trajectory Design Technology for the Long-Range Air-Defense Missile [J].Systems Engineering and Electronics，2003,25(3):304-307.

[6] 王志剛,嚴輝，陳士櫓.軌跡/飛行器總體參數的一體化優化方法研究[J].飛行力學，1997,15(2):19-26.

WANG Zhi-gang, YAN Hui, CHEN Shi-lu. Study of Integrated Optimization Method of Trajectory/Vehicle Overall Parameter [J]. Flight Dynamics, 1997, 15(2):19-26.

[7] 胡凡，楊希祥，江振宇，等，固體運載火箭軌跡/總體參數一體化優化設計研究[J].固體火箭技術，2010,33(6):599-602.

HU Fan,YANG Xi-xiang, JIANG Zhen-yu，et al. Integrated Optimization Design of Trajectory/System Parameters for Solid Launch Vehicles[J].Journal of Solid Rocket Technology, 2010,33(6):599-602.

[8] 劉興洲.飛航導彈動力裝置(上)[M].北京：中國宇航出版社，1992.

LIU Xing-zhou. Cruise Missile Power Device (Volume 1) [M]. Beijing: China Astronautic Publishing House, 1992.

[9] BENSON D A, HUNTINGTON G T, THORVALDSEN T P,et al. Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method[J]. Journal of Guidance, Control and Dynamics, 2006, 29(6):1435-1440.

[10] BENSON D A. A Gauss Pseudospectral Transcription for Optimal Control [D]. Boston: Massachusetts Institute of Technology, 2004.

[11] 宗群，田柏苓，竇立謙. 基于Gauss偽譜法的臨近空間飛行器上升段軌跡優化[J].宇航學報,2010,31(7):1775-1781.

ZONG Qun,TIAN Bai-ling,DOU Li-qian.Ascent Phase Trajectory Optimization for Near Space Vehicle Based on Gauss Pseudospectral Method[J].Journal of Astronautics, 2010,31(7):1775-1781.

[12] BOGGS P T, TOLLE J W. Sequential Quadratic Programming [J].Journal of Acta Numerica, 1995(4):1-51.