飛行器末制導系統(tǒng)線角振動環(huán)境模擬試驗技術*

蘇華昌，姜虹，胡亞冰

(1．北京強度環(huán)境研究所，北京 100076； 2. 北京電子工程總體研究所，北京 100854)

0 引言

末制導控制系統(tǒng)是飛行器的核心和關鍵部分，在很大程度上決定著飛行器的性能，特別是制導精度。一些用于攔截的飛行器，為了實現(xiàn)高機動，采用脈沖發(fā)動機來產(chǎn)生所需要的控制力和力矩。通常飛行器是一個彈性體,在受到載荷作用時,就會引起彈體的彈性變形。在末制導過程中，發(fā)動機工作會給彈體造成較大的沖擊力，除了產(chǎn)生控制所需的剛體姿態(tài)運動外，受飛行器結構彈性影響，還會導致較大高頻彈體彈性線角振動環(huán)境。由于慣組和導引頭敏感器件的感應，會將這些高頻擾動引入控制系統(tǒng)，影響末制導系統(tǒng)的穩(wěn)定性和精度，嚴重時會導致目標從導引頭很小的瞬時視場中丟失[1-2]。

為了考核飛行器末制導性能，有必要對脈沖發(fā)動機工作帶來的影響進行地面試驗評估。目前，轉(zhuǎn)臺是測試導引頭和慣性器件性能的有效工具，它能模擬彈體姿態(tài)角運動，通過實物仿真來測試導引頭和慣組性能[3]。但是，由于轉(zhuǎn)臺帶寬較低，不能模擬高頻的角振動環(huán)境，而且轉(zhuǎn)臺承載能力有限，不能負載整個末制導彈體，無法考核結構彈性對控制系統(tǒng)的影響。另外，飛行器通常要進行線振動環(huán)境試驗檢驗，由于沒有疊加角振動環(huán)境，也難以真實檢驗末制導系統(tǒng)性能。為了合理對飛行器末制導系統(tǒng)進行性能檢驗，必須設計一個合理可行的地面模擬考核方案，準確模擬發(fā)動機工作帶來的彈體動力學環(huán)境，通過地面試驗來檢驗末制導系統(tǒng)的性能和精度，降低飛行風險和研制成本。

本文介紹了一種旨在考核脈沖發(fā)動機工作下末制導系統(tǒng)性能的模擬試驗技術。首先，利用多維振動試驗技術，設計了一個能實現(xiàn)進行線角振動聯(lián)合加載的試驗系統(tǒng)。然后，采用多維傳遞率矩陣和激勵反推識別的方法，間接再現(xiàn)了線角振動時域響應波形；最后，通過地面數(shù)據(jù)和遙測數(shù)據(jù)的對比分析，對模擬的真實性進行了評估。

1 地面試驗系統(tǒng)設計

飛行器在實際飛行中，承受的是六自由度振動環(huán)境，即3個方向線振動和繞3個方向的角振動同時存在。但受到試驗設備水平的限制，早期只在單個振動臺上進行單向的線振動環(huán)境模擬。隨著電子技術的高速發(fā)展、振動控制理論的創(chuàng)新、多維振動試驗系統(tǒng)的商業(yè)化出現(xiàn)，使得六自由度振動環(huán)境模擬變?yōu)榭赡埽瑖獾囊恍┲匾娇蘸教靹恿W研究室已經(jīng)開始了相關試驗研究[4-7]。多維振動試驗技術的出現(xiàn)，為使用電磁振動臺來模擬角振動提供了技術支撐，電磁振動臺帶寬很高，能滿足高頻角振動模擬要求。在最新的美軍標810G的多激勵試驗方法中，就明確提出了有關角振動概念和模擬方法。基于剛體運動學原理，可以通過2個振動激勵設備，來構造圖1所示的試驗系統(tǒng)[8]。當2個激勵設備同幅值同相激勵時，可以實現(xiàn)z軸單純線振動；當2個激勵設備同幅值反相激勵時，可以實現(xiàn)繞x軸單純角振動。這2種形式稱為多激勵單軸試驗形式(multi-exciter/single-axix,MESA)。當2個激勵幅值和相位各自獨立時，系統(tǒng)可以同時實現(xiàn)z軸線振動和繞x軸角振動，此形式稱為多激勵多軸試驗形式(multi-exciter/multi-axis,MEMA)，它為飛行器在試驗室進行線角振動環(huán)境模擬提供了技術可行性。

地面模擬試驗需要使用真實的力學環(huán)境，現(xiàn)有的慣組角速率和遙測點線振動環(huán)境，代表了飛行器跟蹤目標過程中控制系統(tǒng)工作導致的彈體響應，模擬了該環(huán)境就實現(xiàn)了地面試驗與飛行環(huán)境的高度相關。由于遙測環(huán)境呈典型的非平穩(wěn)特征，最真實的辦法就是直接進行時間歷程再現(xiàn)。但是，要再現(xiàn)遙測的線角振動時間歷程，存在幾個難點。首先，遙測點雖然測量的是線振動，但不在彈體端面中心，響應存在著耦合，由于測量自由度不足，無法解耦。其次，遙測點與慣組不在彈體同一端面內(nèi)，而且慣組角振動環(huán)境是減振后的角速率響應，帶有非線性的減振器環(huán)節(jié)，大大增加了試驗模擬的復雜性。最后，受多維波形復現(xiàn)試驗技術的限制，目前很難直接通過響應控制的方式進行角速率時間歷程復現(xiàn)。基于以上原因，不考慮直接去復現(xiàn)遙測位置的線角振動響應。

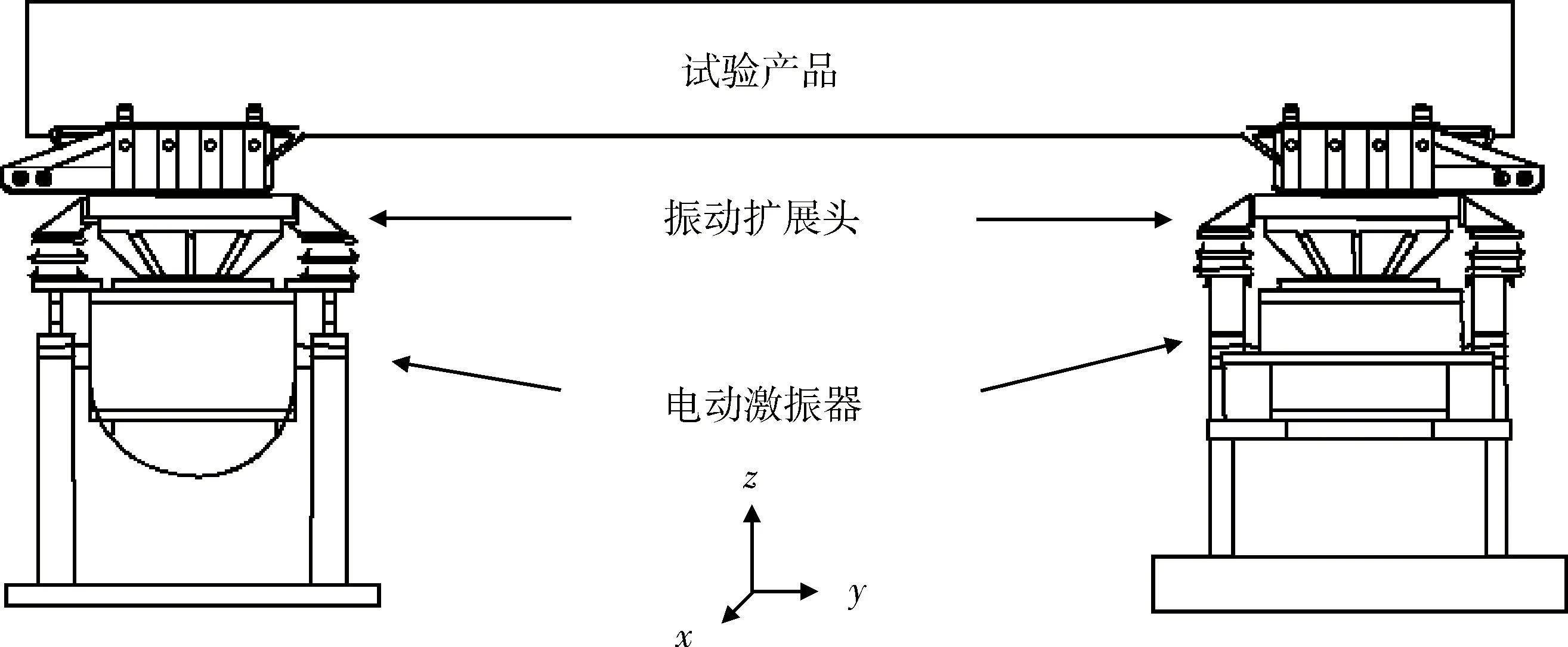
圖1 MESA試驗形式Fig.1 MESA test form

通過激勵源分析，在末制導飛行過程中，彈體控制通過脈沖發(fā)動機來實現(xiàn)，彈體的力學環(huán)境主要是由發(fā)動機工作時的瞬態(tài)激勵造成的，氣動力影響很小，因此，可以通過振源模擬的方式來復現(xiàn)響應，只要振源模擬得比較準確，那么彈體線角響應就會得到準確再現(xiàn)。基于MEMA試驗方法，設計了一套雙臺激勵的試驗系統(tǒng)，來進行線角振動聯(lián)合加載模擬，系統(tǒng)如圖2所示。該系統(tǒng)設計了一個特殊工裝，工裝底部兩端分別連接2個振動臺，工裝上端與彈體發(fā)動機端面相連，來模擬脈沖發(fā)動機工作激勵。

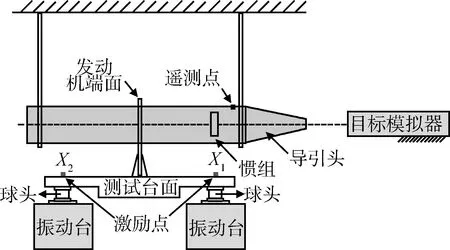
圖2 末制導系統(tǒng)線角振動試驗示意圖 Fig.2 Linear and angular vibration test system for terminal guidance system

試驗時，控制工裝端面的2個激勵點，可以通過調(diào)整激勵大小和相位的變化來形成線振動和角振動，通過發(fā)動機端面?zhèn)鬟f給彈體，實現(xiàn)線角振動環(huán)境模擬。試驗需要復現(xiàn)的2個響應在2個端面：一個是遙測點的線振動，一個是慣組的角速率響應。當使用2個激勵時，輸入輸出的數(shù)目相同，其解是可以唯一確定，從而理論上可以通過2個激勵點來模擬，來間接復現(xiàn)出所需的線角響應環(huán)境。為了檢驗飛行器性能，可在導引頭前方放置了目標模擬器，試驗前整個控制系統(tǒng)通電工作，進行目標對準，然后通過施加線角振動環(huán)境，檢驗導引頭的跟蹤穩(wěn)定性和精度，并同時進行導航模擬，考核慣組和整個控制系統(tǒng)性能。

2 線角振動時域間接模擬方法

如果間接實現(xiàn)遙測線角環(huán)境時域波形復現(xiàn)，需要知道激勵的時域波形，2個激勵點的時域波形可以通過類似載荷識別的方法來獲得。載荷識別是指在結構動態(tài)特性已知的情況下，通過測量的響應，反推出施加的激勵載荷[9]。為了反推出激勵，需要通過試驗獲得激勵點與響應點之間的傳遞關系。由于激勵和響應的數(shù)量超過了1個，屬于多維激勵試驗范疇，需要引入多維傳遞率測量和激勵推導方法。

2.1 多維傳遞率測量原理

對于一個時不變的線性系統(tǒng)，結構上各點之間總是存在一定的傳遞關系，可以通過隨機振動試驗來獲得它們之間的傳遞率矩陣。在平穩(wěn)隨機激勵條件下，假定2個振動臺激勵X分別為X1和X2，規(guī)定位置處的線角響應R分別為RL和RA，在頻域可以得到[10]

即

R(f)=HRX(f)X(f)，

(1)

式中：R(f)為響應的傅氏譜矩陣；X(f)為激勵的傅氏譜矩陣；HRX(f)為傳遞率矩陣。

兩邊乘以輸入X(f)的共軛轉(zhuǎn)置，得到：

即

GRX(f)=HRX(f)GXX(f)，

(2)

式中:GRX為激勵與響應互譜矩陣；GXX為激勵的自譜矩陣。

只要輸入之間相不互關，則GXX可以求逆，從而可以求出傳遞函數(shù)矩陣為

HRX(f)=GRX(f)GXX(f)-1.

(3)

因此，通過多自由度激勵，同時測量激勵和需模擬位置的響應，則可以獲得整個傳遞矩陣。

2.2 傳遞率矩陣測量

為了獲得激勵點與模擬點之間的傳遞關系，進行了全彈傳遞試驗。在傳遞試驗時，以工裝上2個激勵點的線振動為輸入，以遙測點的線振動和慣組的角速率為輸出，用雙臺激勵的方式進行試驗，通過式(3)來計算遙測點線振動和慣組角速率對激勵點的多維傳遞率矩陣。由于激勵基于試驗傳遞率矩陣推導來得到，傳遞率矩陣測量的質(zhì)量就顯得尤為重要。試驗測得的傳遞率矩陣如圖3所示，可以看出，試驗獲取的曲線非常光滑，保證了激勵推導的精度。

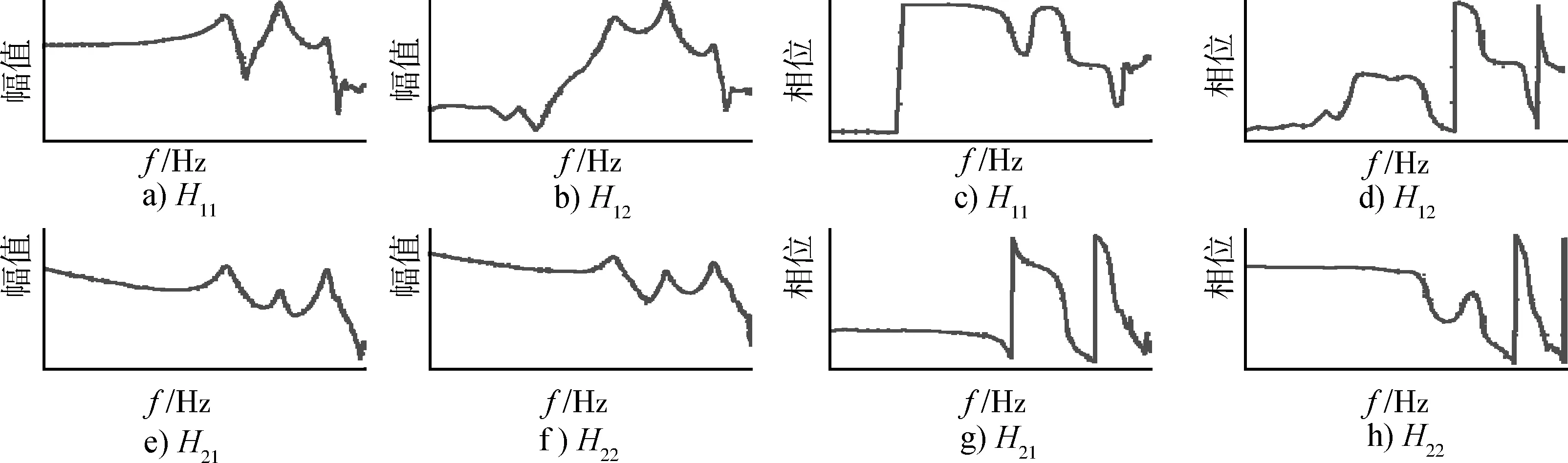
圖3 傳遞率矩陣實測曲線Fig.3 Curves of transfer matrix on the spot survey

2.3 已知傳遞率矩陣和響應反推輸入

在已知傳遞率矩陣HRX(f)和響應R(f)的情況下，通過式(1)，可以反推出激勵輸入。假定需要模擬位置的線角自由度的時域響應分別為{rl(t)，ra(t)}，所需反推的線振動激勵X的時域曲線分別為{x1(t)，x2(t)}。由于R為發(fā)動機開關工作下的結構響應，呈現(xiàn)典型的瞬態(tài)特征。對于瞬態(tài)信號而言，激勵和響應均非周期函數(shù)，絕對可積，滿足狄利克雷條件，根據(jù)卷積定理，將激勵和響應都轉(zhuǎn)化到頻域內(nèi)，可得它們之間的關系為[11-12]

(4)

式中：BRX(f)為HRX的逆，由于線振動響應rl與角速率響應ra與激勵x1和x2都有關。

由卷積定理可知，頻域的乘積等于時域的卷積，使用卷積定理將式(4)轉(zhuǎn)化到時域，可以得到

(5)

這樣，使用需要間接模擬的時域數(shù)據(jù)，通過卷積的方式，就能直接得到激勵的時間歷程。

2.4 多維激勵導出結果

利用2.3中的公式(5)，對需要模擬的慣組角速率和遙測點線振動時域波形進行適當預處理后，結合傳遞試驗獲得的多維傳遞矩陣HRX(f)，推導出了2個激勵點的線振動時域波形，如圖4所示。因為試驗要復現(xiàn)線角振動環(huán)境，激勵端面必然含有線振動和角振動2個自由度信息。對于多維振動時域波形再現(xiàn)，角振動自由度的信息通常以相干和相位的形式隱含在時域波形中，圖5給出了2個激勵點隱含的相干和相位信息。可以看出，為了間接實現(xiàn)所需的線角振動響應，2個輸入激勵的相干和相位是隨頻率變化的。獲得激勵的時域波形后，就能實現(xiàn)地面試驗模擬。

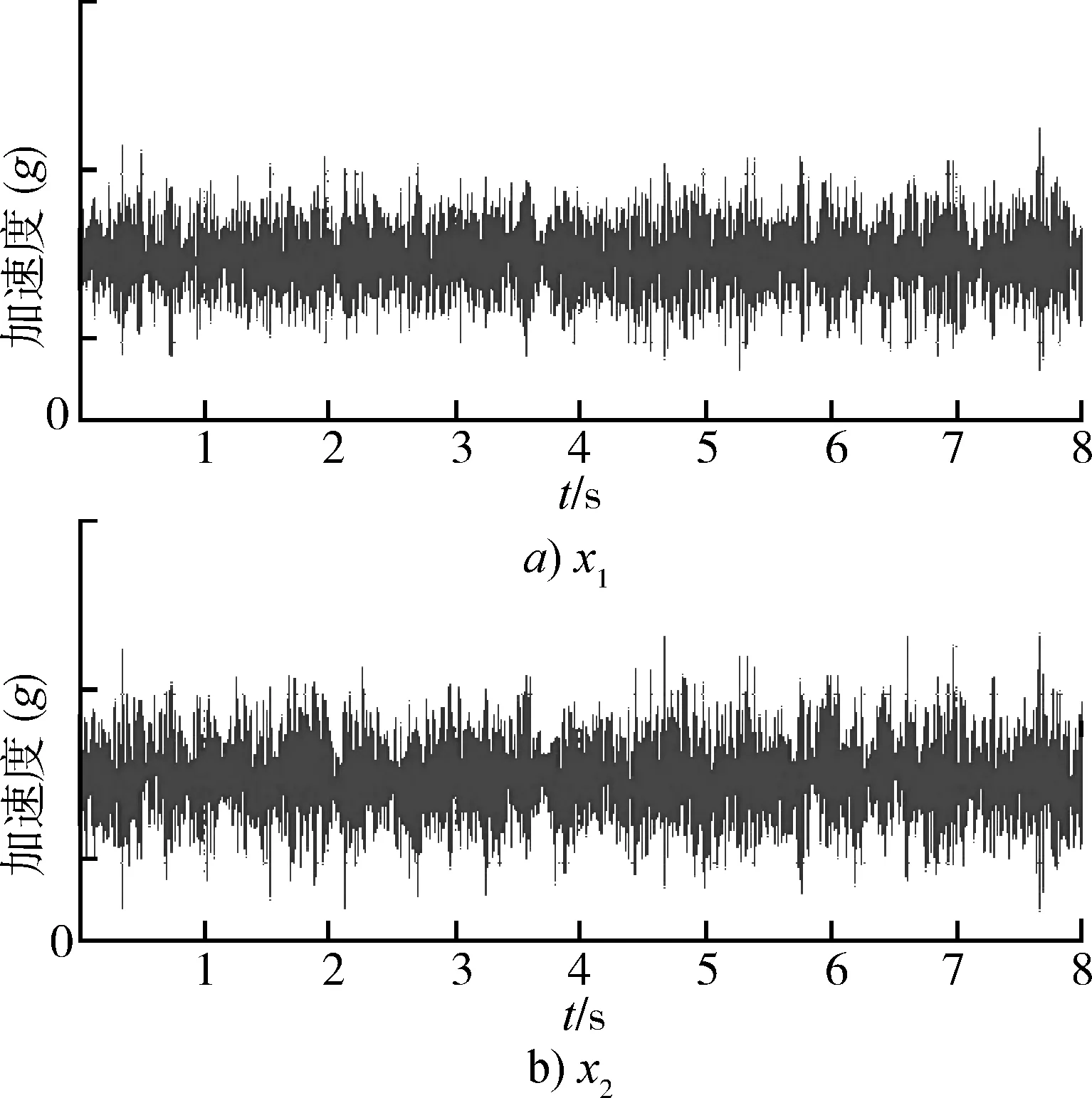
圖4 導出2個激勵點時域波形Fig.4 Waveform on time domain of the two excitation point

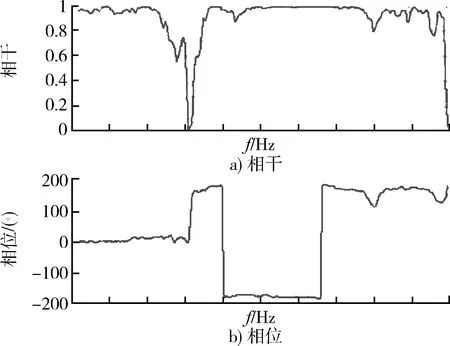
圖5 激勵之間的相干和相位關系Fig.5 Coherence and phase between the two excitations

3 模擬真實性檢驗

飛行器地面試驗考核結果直接關系到其指標是否滿足設計要求，因為線角振動環(huán)境通過間接方式來模擬，模擬的真實性對于性能評判非常重要，有必要對間接模擬的真實性進行檢驗。在試驗時，控制儀只能對2個激勵點的時域波形進行誤差修正，不能直接修正間接模擬的線角響應，因此只能通過對試驗響應數(shù)據(jù)分析來分析模擬精度，評估地面試驗真實性。利用導出的2個激勵點時域波形，對飛行器進行了線角振動波形復現(xiàn)調(diào)試試驗，以檢驗地面試驗模擬的真實性，檢驗從頻域和時域2個方面進行。

3.1 頻域內(nèi)檢驗

將試驗調(diào)試的實測響應處理成功率譜，與對應位置遙測信號功率譜進行對比，在頻域內(nèi)檢驗關鍵共振頻率和整個譜密度曲線的一致性。試驗調(diào)試與遙測結果的一致性越高，證明試驗模擬越真實，圖6給出試驗調(diào)試和遙測原始結果的對比曲線。可以看出，在小量級下，模擬線角功率譜與遙測結果相差很小，各個主要的共振頻率都得到了完全復現(xiàn)，試驗模擬的精度非常高。在大量級情況下，模擬線角功率譜與遙測結果的主要特征也基本相同，只是高頻段有一定放大，但是對于地面模擬考核來說，結果是保守的。放大主要是慣組減振器非線性造成的，因為模擬的角速率是減振后的響應，傳遞推導中包含了減振器特性，造成了一定的量級非線性。

3.2 時域內(nèi)檢驗

受脈沖發(fā)動機的激勵影響，遙測點的線振動時域波形具有很強的非平穩(wěn)特性，以短脈沖波形的形式重復，這是此類導彈飛行環(huán)境的一個重要時域特征，因此，可以將地面模擬的遙測點波形和遙測結果進行相比對，檢驗其時域特性的相似性，作為地面試驗模擬真實性的另一度量。圖7給出了小量級調(diào)試時遙測點線振動的模擬對比曲線。可以看出，地面試驗將脈沖發(fā)動機的瞬態(tài)激勵進行了很好的模擬，完全復現(xiàn)了飛行環(huán)境的時域典型特征，證明試驗模擬真實性很強。

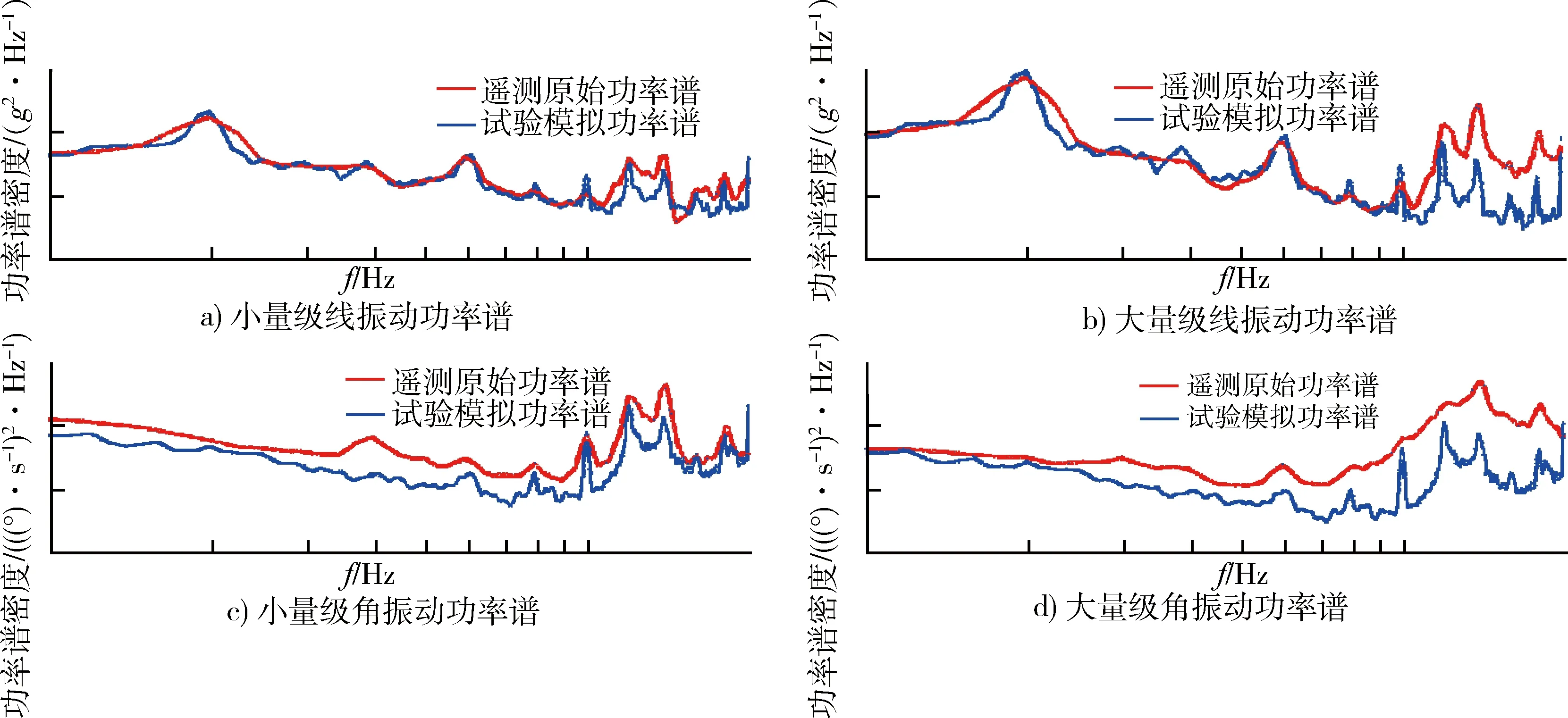
圖6 試驗模擬與遙測原始線角功率譜對比Fig.6 Comparison of linear and angular power spectral density between the test simulation and telemetric data

圖7 遙測點模擬的時域特征對比Fig.7 Comparison of the test simulation and telemetric data in time domain character

4 結束語

(1) 本文利用多維振動試驗技術，通過雙臺激勵的方式實現(xiàn)了飛行器線角振動聯(lián)合加載模擬。該試驗方式克服了轉(zhuǎn)臺模擬帶寬不足的缺陷，有效地模擬了彈體高頻角振動，并同時施加了線振動環(huán)境，增加了地面試驗的真實性。

(2) 基于遙測線角振動時域數(shù)據(jù)和測量的多維傳遞函數(shù)矩陣，反推出試驗所需線振動激勵條件，通過控制激勵點的線振動時域波形，間接再現(xiàn)了飛行線角振動環(huán)境，解決了線角時域同時模擬的難題。

(3) 通過振源分析，選擇了發(fā)動機端面作為激勵傳遞端面，從而對飛行時發(fā)動機工作造成的彈體響應進行真實模擬。試驗數(shù)據(jù)表明，遙測信號的各個主要共振頻率都得到了很好復現(xiàn)，其時域模擬典型特征也非常相似，試驗模擬真實性很好。

利用該項試驗技術，成功對飛行器進行了地面試驗模擬，考核了末制導系統(tǒng)的穩(wěn)定性和精度，并檢驗了系統(tǒng)各部件的性能，取得了良好效果。該技術通過地面試驗模擬對飛行器末制導系統(tǒng)進行系統(tǒng)級考核，提供了有效的地面研究手段，可以降低飛行試驗風險和研制成本，該試驗技術也可為其他飛行器末制導系統(tǒng)地面考核提供參考，具有較好的應用價值。

參考文獻：

[1] 程云龍,丘淦興,趙善友,等. 防空導彈自動駕駛儀設計[M]. 北京:中國宇航出版社, 1993.

CHENG Yun-long,QIU Gan-xing,ZHAO Shan-you,et al. Air Defense Missile Autopilot Design[M]. Beijing: China Astronautic Publishing House, 1993.

[2] David H Titterton, John L Weston.Strapdown Interial Navigation Technology Second Edition[M].Copublished by the Institution of Engineering and Technology,London,United Kingdom and the American Institute of Aeronautics,Reston,Virginia,USA:IEE?, 2004.

[3] 劉興堂. 導彈制導控制系統(tǒng)分析、設計與仿真[M]. 西安:西北工業(yè)大學出版社, 2006.

LIU Xing-tang. Missile Guidance Control System Analysis, Design and Simulation[M]. Xi’an: Northwestern Polytechnical University Press, 2006.

[4] SMALLWOOD DAVID O.Multiple Shaker Random Vibration Control-An Update[C]∥Proceedings of the IEST,Ontario,California,USA,1999:212-221.

[5] STROUD R C,HAMMA G A,UNDERWOOD M A.A Review of Multiaxis Multiexciter Vibration Technology[J].Sound and Vibration,1996,30(4):20-27.

[6] UNDERWODD M A,KELLER T. Recent System Developments for MultiActuator Vibration Control[J].Sound and Vibration,2001,246(4):2-8.

[7] Alan Kenny. The Do’s and Don’ts of Multi-Shaker Testing[C]∥50th ATME of ESTCH,IEST,Las Vegas,Nevada,USA,2004: 274-284.

[8] MIL STD 810G, Department of Defense Test Method Standard [S].

[9] 傅志方. 振動模態(tài)分析與參數(shù)辨識[M]. 北京:機械工業(yè)出版社, 1990.

FU Zhi-fang. Modal Analysis and Parameter Identification [M]. Beijing: China Machine Press,1990.

[10] Cyril M Harris,Allan G Piersol. Harris' Shock and Vibration Handbook[M].5th ed.New York,USA:McGRAW-HILL,2002.

[11] Charles L phillips, John M Parr, Eve A Riskin.Signals,Systems,and Transforms,[M].3rd ed.Upper Saddle River, USA:Prentice Hall, 2003.

[12] Bendat, Julius S,Allan G Piersol. Random Data Analysis and Measurement Procedures [M].3rd ed.Hoboken,USA:John Wiley & Sons, 2000.