一種滿足布魯斯特角約束的導引律研究*
王國勝,李蕓
(北京電子工程總體研究所,北京 100854)
0 引言
由于地形或者地海雜波的影響,雷達一般難以對超低空目標進行探測,使得超低空突防成為一種常用的突防手段。隨著各國掠海飛行技術的發展,研究具有超低空反導能力的防空導彈已經刻不容緩[1-2]。
和普通的目標相比,超低空目標特性有其特殊之處。雷達導引頭測量超低空目標時受地海雜波影響而引起的多路徑效應嚴重[3-4],測量精度下降,如果不對視線角進行約束,將導致制導精度嚴重惡化。研究表明,當擦地角在布魯斯特角附近時,地海雜波反射系數最小[5],導引頭測量精度較高。所以,約束擦地角對提高制導精度有重要意義。本文仿真中已對擦地角和視線角進行了轉換,將以視線角進行計算。
現役防空導彈大多采用比例導引律或修正的比例導引律[6-8],而導彈按照經典比例導引彈道飛行時,其視線角基本取決于導彈的初始發射信息,一般無法滿足布魯斯特角約束。本文對經典比例導引律進行了改進,使得無論導彈初始處于什么位置,都能將視線角調整到布魯斯特角附近。
1 數學模型
圖1是導彈攔截目標示意圖,圖中角度以逆時針方向為正,如圖中所示的情況下,視線角q和導彈速度方向與基準線夾角θ應當為負值[9]。
導彈攔截目標模型包括:彈目相對運動模型、彈體與穩定控制系統動態響應模型、導引頭測量模型及誤差模型。其簡化方框圖如圖2所示。
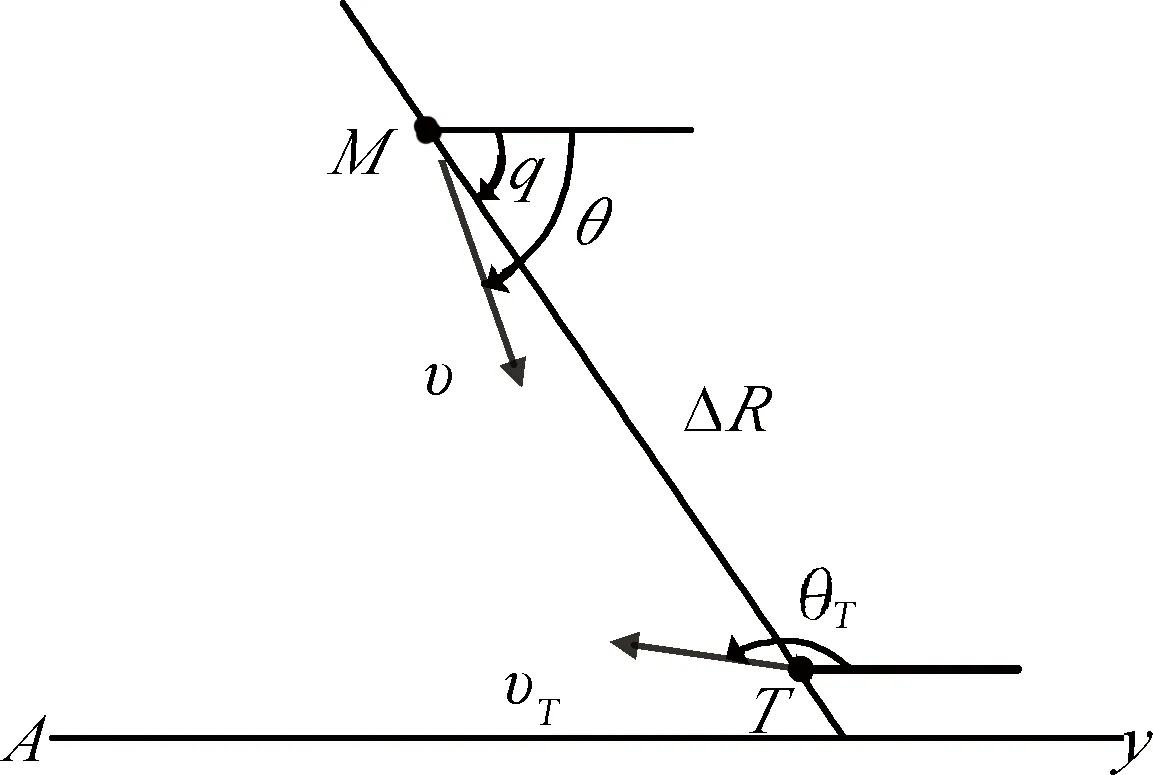
圖1 彈目相對運動關系Fig.1 Relative motion of missile and target
假定導彈和目標在同一固定平面內運動(即攻擊平面),彈目相對運動模型為
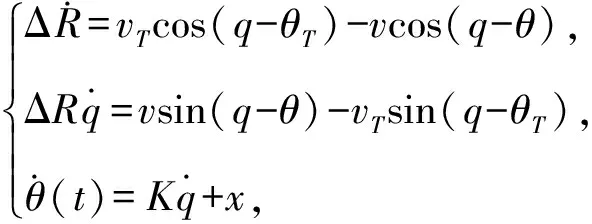
(1)
式中:ΔR為彈目相對距離;v為導彈速度;vT為目標速度;θT為目標速度方向與基準線夾角;x為補償量。
實際飛行中,導彈跟蹤控制指令時會有延時和超調;導引頭測量得到的視線轉率和真值相比不但有滯后,還包含噪聲。在基礎研究模型中,彈體與穩定控制系統動態響應環節可以等效為一個一階慣性環節1/(T1s+1);導引頭測量得到的視線轉率可以認為是實際視線轉率通過一個一階慣性環節1/(T2s+1),再加上噪聲得到。這里的噪聲按照有色噪聲來考慮[10]。
綜上所述,就得到一個考慮了導引頭環節和彈體與穩定控制系統動態響應環節的彈目相對運動數學模型如下:
(2)
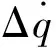
2 改進的比例導引律
2.1 地海雜波的特性
一般情況下,大地或大海可以看作半導電媒質,而地海雜波正是雷達天線所發射的電磁波經地面或海面反射而形成的反射波。根據電磁波理論,平面電磁波可分解為水平極化波和垂直極化波,并且,其反射波極化方式不變。可以證明,垂直極化的電磁波由空氣斜入射到半導電媒質時,地海雜波的反射系數隨入射角變化劇烈,如圖3所示:入射角小時,其反射系數趨近于1,并隨入射角增大快速下降;下降到一定值后,再增加入射角又會引起反射系數的迅速增加;沒有無反射點,但存在最小反射點,通常將產生最小反射的入射角稱為布魯斯特角[11]。

圖2 導彈攔截目標模型方框圖Fig.2 Block diagram of missiles intercepting targets
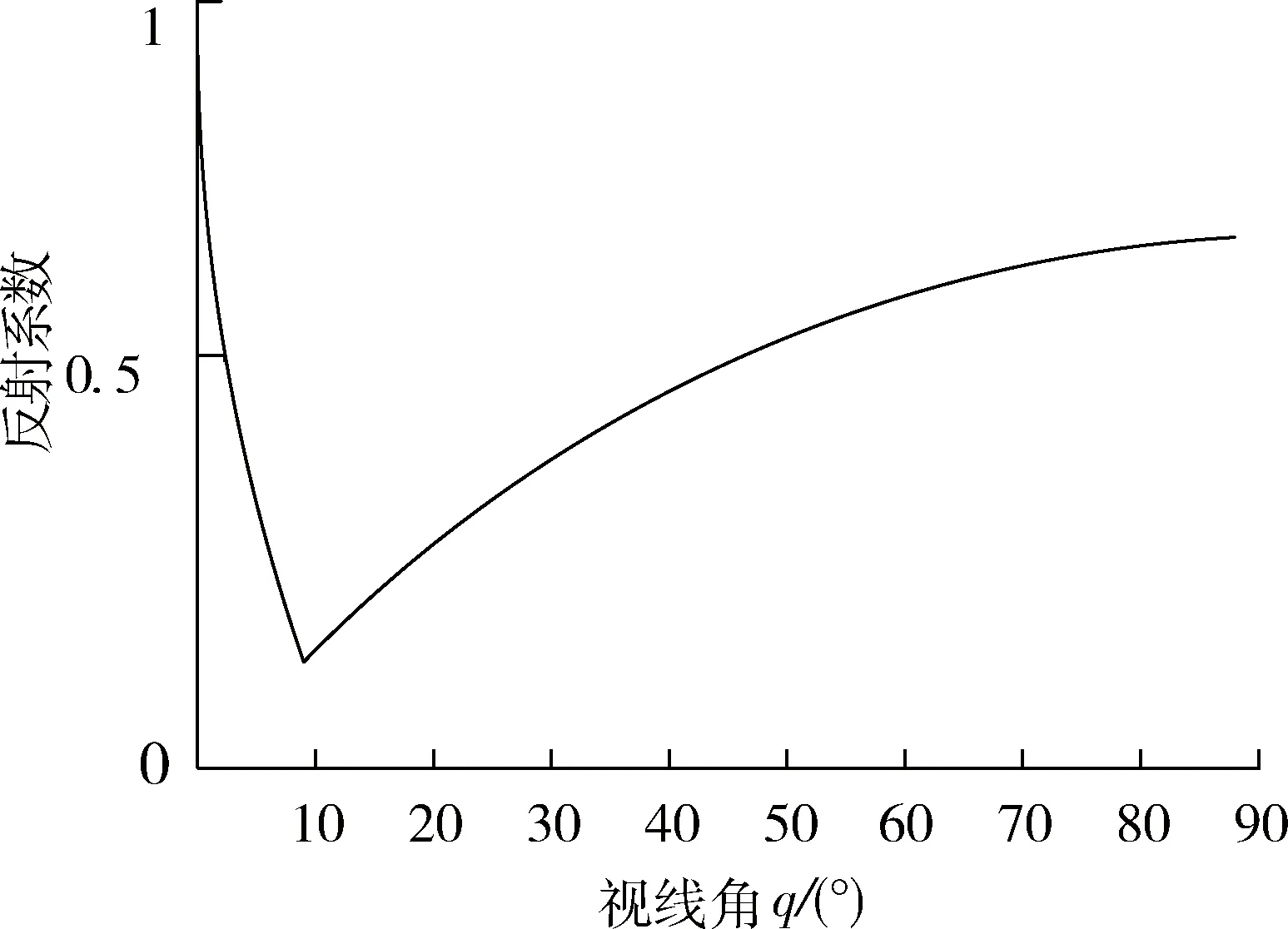
圖3 海雜波反射系數Fig.3 Reflection coefficient of sea clutter
導引頭在截獲和跟蹤目標時,真實目標回波和經地面或海面反射的目標回波均落入導引頭波束范圍內,形成目標的多路徑效應。如果此問題解決不好,將嚴重惡化制導精度。當入射角在布魯斯特角附近時,反射系數最小,能有效保證導引頭的測量精度。
2.2 視線轉率的控制規律設計
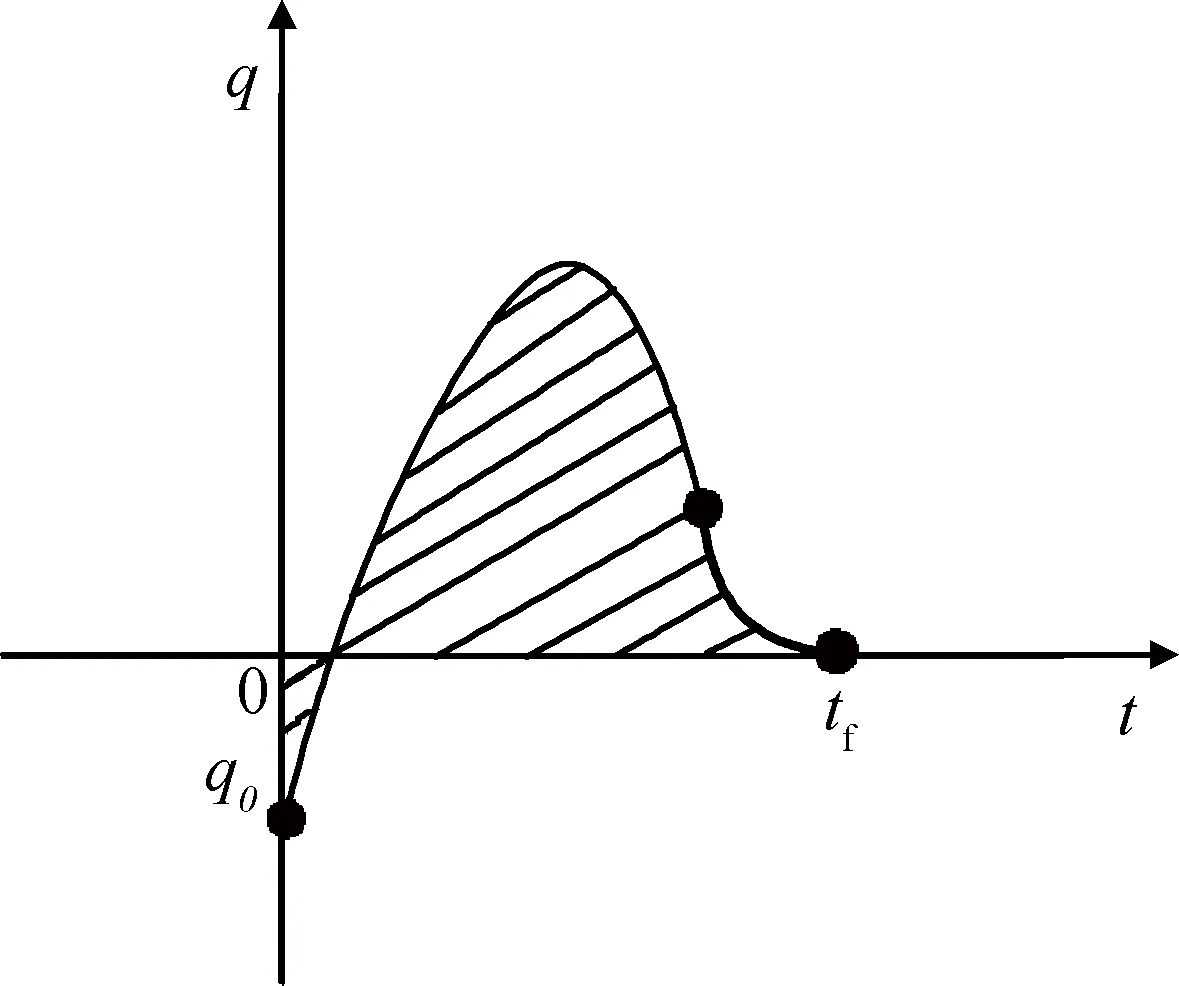
圖4 視線轉率變化曲線Fig.4 Changing curve of sight angular velocity
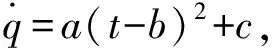
(3)
a(tf-b)2+c=0,
(4)
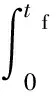
(5)
取定tf后,由式(3)~(5)可求得a,b,c。
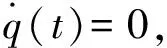
(6)
a(tf-b)2=0,
(7)
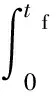
(8)
由式(6)~(8)可以解出tf,a,b。
(9)
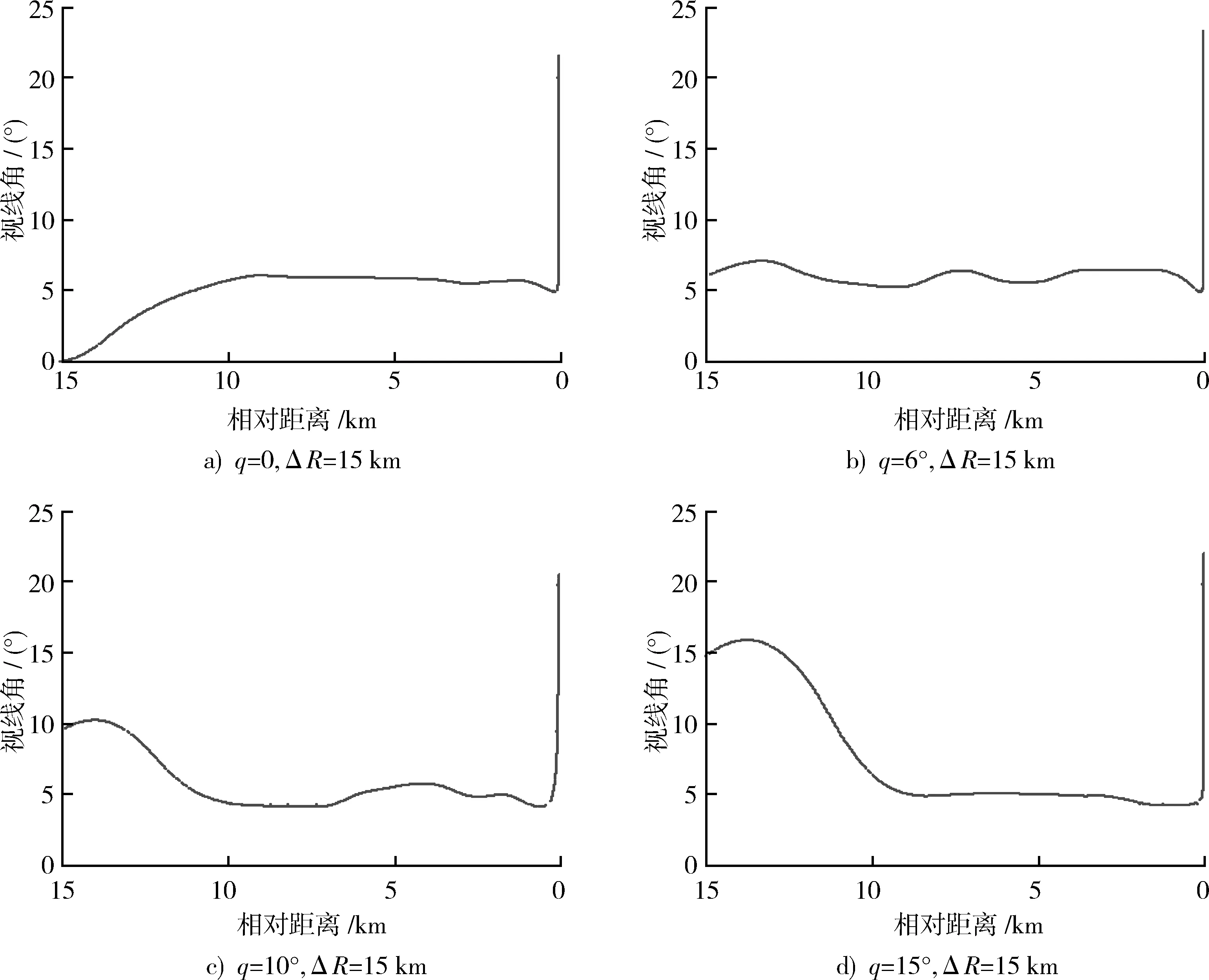
對于的q>qb情況,其計算過程與q (10) (11) 改進后的比例導引律形式為 (12) 仿真計算條件為: 穩定回路時間常數T1=0.3 s; 導引頭滯后常數T2=0.2 s; 導引頭噪聲為均值為-0.1 (°)/s,均方根值為1 (°)/s的高斯分布的白噪聲通過一個成型濾波器,得到有色噪聲; 布魯斯特角qb=6°。 期望通過數學仿真研究改進后比例導引律的控制效果。 取初始相對距離ΔR=15 km,初始視線角分別為q0=0°,6°,10°,15°,仿真后可得到圖5。由圖5可以看出,相對距離一定時,對于不同的初始視線角,通過改進的比例導引律進行導引時,可將視線角控制到布魯斯特角附近并保持。 取初始視線角q0=10°,初始相對距離分別取為ΔR=12,20 km,仿真后得到圖6。可以看出,對于不同的初始相對距離,同樣可以控制視線角到布魯斯特角附近并保持。 圖5 視線角變化曲線Fig.5 Changing curve of line-of-sight angle 圖6 視線角變化曲線Fig.6 Changing curve of line-of-sight angle 以q=10°,ΔR=15 km為例,分別對不加補償量和加入補償x進行仿真計算,仿真次數為100次,得到脫靶量[12]分布圖7a)和7b)。對比圖7a)和圖7b),可以得到結論:加補償量后對脫靶量無明顯影響。 圖7 脫靶量分布Fig.7 Distribution of miss distance 攔截超低空目標時,雷達導引頭的多路徑效應將嚴重影響導彈制導精度。通過約束視線角,可有效抑制多路徑效應,提高導引頭測量精度。本文研究了滿足布魯斯特角約束的改進型比例導引律,并進行了仿真研究。仿真結果表明,本文給出的導引律能夠有效約束視線角,而且補償項對脫靶量無明顯影響。 參考文獻: [1] 陳兵. 面向反艦導彈超低空突防效能分析的仿真系統研究[J]. 戰術導彈技術,2009(6):85-89. CHEN Bing. Research on Simulation System Based on Very Low Altitude Penetration Effectiveness Analysis of Anti-Ship Missile[J]. Tactical Missile Technology,2009(6):85-89. [2] 劉躍龍,張艷. 超低空引信技術綜述[J]. 制導與引信,2010(4):22-26. LIU Yue-long,ZHANG Yan. Summarization of Low Altitude Fuze Technology[J].Guidance and Fuze,2010(4):22-26. [3] 李彥佐,金亞秋. 隨機粗糙海面的多路徑海雜波頻譜數值模擬[J]. 微波學報,2005,21(4):6-11. LI Yan-zuo,JIN Ya-qiu. Numerical Simulation of Multi-path Clutter Spectrum of Randomly Rough Oceanic Surface[J]. Journal of Microwares,2005,21(4):6-11. [4] 劉永義,黨亞民,薛樹強. 海面環境多路徑效應建模研究[J]. 大地測量與地球動力學,2011,31(2):121-124. LIU Yong-yi,DANG Ya-min,XUE Shu-qiang. Research on Multipath Model of Sea Surface[J]. Journal of Geodesy and Geodynamics,2011,31(2):121-124. [5] 任子西. 不同入射余角情況下海面電波特性對雷達導引頭的影響分析[J]. 戰術導彈技術,2009(4):1-6. REN Zi-xi. Analysis of the Influence of Sea Radio Wave on Radar Seeker Under Different Incidence Angle Conditions[J]. Tactical Missile Technology,2009(4):1-6. [6] GUELMAN M. The Closed-Form Solution of Pure Proportional Navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976,12(7):526-532. [7] GUELMAN M. Optimal Guidance Law in the Plane[J]. Journal of Guidance,1984,7(4):471-476. [8] GUELMAN M. A Qualitative Study of Proportional Navigation[J]. IEEE Transactions on Aerospace and Electrionic Systems,1971,7(3):638-643. [9] 錢杏芳,林瑞雄,趙亞男. 導彈飛行力學[M]. 北京:北京理工大學出版社.2000. QIAN Xin-fang,LIN Rui-xiong,ZHAO Ya-nan. Dynamics of Missile[M]. Beijing:Beijing Institute of Technology Press,2000. [10] BARTOSCH L. Generation of Colored Noise[J]. International Journal of Modern Physics. C, Physics and Computers,2001,12(6):26-30. [11] 章惠君. 抗地雜波干擾的最優導引律[J]. 航空兵器,2004(3):30-31. ZHANG Hui-jun. Optimal Guidance Law of Anti-Interference of Earth Clutter[J]. Aero Weaponry,2004(3):30-31. [12] 李志宇,吳嗣亮,魏國華. 一種快速的矢量脫靶量測量算法[J]. 現代防御技術,2007,35(5):63-66. LI Zhi-yu,WU Si-liang,WEI Guo-hua. Measurement of Vector Miss distance Based on LFM Signal Model[J]. Modern Defence Technology,2007,35(5):63-66.2.3 補償量的計算
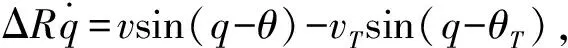
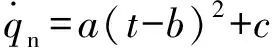
3 仿真結果與分析
3.1 不同初始視線角的仿真研究
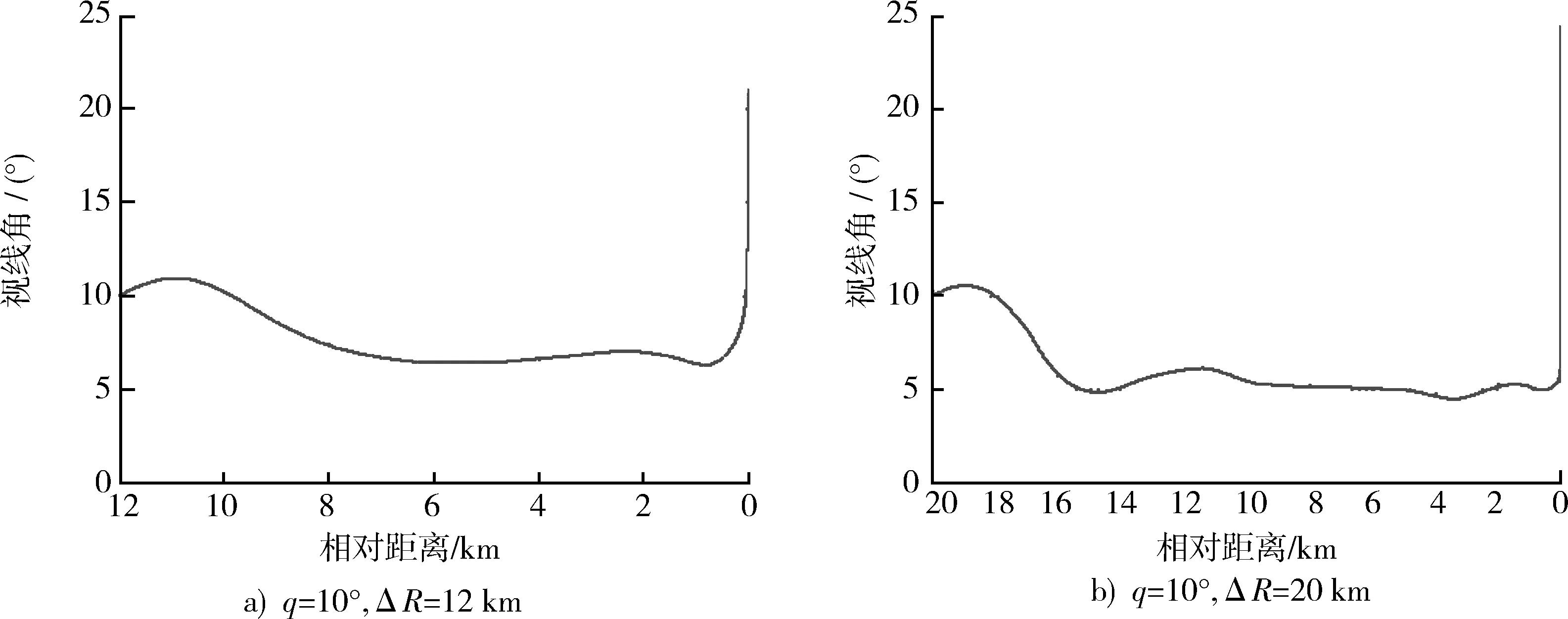
3.2 不同初始相對距離的仿真研究
3.3 對脫靶量影響分析
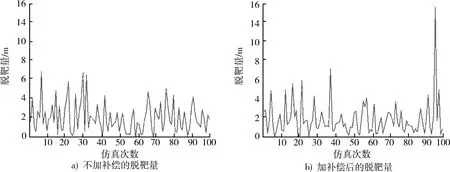
4 結束語

