新的Q整圖類
盧世芳
(青海大學基礎部,青海西寧810016)
盧世芳
(青海大學基礎部,青海西寧810016)
摘要:在他人研究整圖,Laplace整圖和Seidel-整圖的基礎上,刻畫了Q整圖新類.對圖類?的無符號拉普拉斯特征多項式進行研究分析,應用矩陣的初等變換,給出了圖類?是Q整圖的充分必要條件,得到了新的Q整圖類?及其Q譜.
關鍵詞:無符號拉普拉斯譜;無符號拉普拉斯特征多項式;Q整圖
1 引言
本文中所提到的圖都是有限、無向、簡單圖,沒有給出定義的記號和術語參見文獻[1-2].
設圖G的頂點集為V(G),邊集為E(G),A(G)=(aij)n×n是圖G的(0,1)-鄰接矩陣,即當ViVj∈E(G)時,aij=1;當ViVj/∈E(G)時,aij=0.矩陣

分別稱為圖G的Seidel矩陣、Laplace矩陣和無符號Laplace矩陣(或Q矩陣),其中D(G)是圖G的頂點度矩陣.多項式

分別稱為圖G的Seidel矩陣、Laplace矩陣和Q矩陣的特征多項式[2].如果,一個圖G的Seidel矩陣、Laplace矩陣和Q矩陣的特征值都是整數,則圖G分別稱作S-整圖、Laplace整圖和Q整圖.設λ1,λ2,………,λs是圖G的s個不同的無符號Laplace特征值,對應于它們的重數分別是為圖G的無符號Laplace譜.
設Kn是n個頂點的完全圖,是從Kn中刪去互不相鄰的條邊所得的圖類.
有關整圖的研究源于上世紀70年代,文獻[3-4]中對有少數點構成的所有整圖進行了刻畫.文獻[5]中給出了關于整圖的一些結果.文獻[6]中作者給出了完全6-部圖是Seidel-整圖的一個充分必要條件.文獻[7-10]中作者給出了關于Q整圖的一些結果.關于Q整圖新類的刻畫,迄今為止不是很多,具有很好的研究前景.這篇文章將從討論圖類的無符號Laplace特征多項式入手,給出并證明圖類是Q整圖的充分必要條件,得到了新的Q整圖類以及它們的Q譜.
定理2.1設圖是具有n個頂點的完全圖Kn中刪去互不相鄰的條邊所得的圖類.則圖的無符號Laplace特征多項式為:
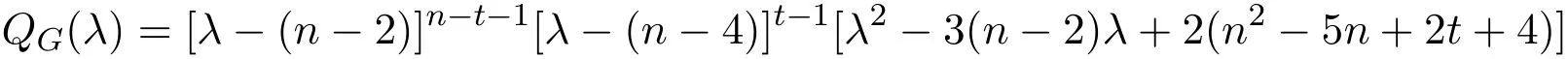
當且僅當方程
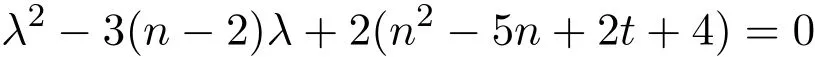
有整根,即當且僅當n2+4n+4?16t是一個完全平方數時,圖類是Q整圖.
證明圖G的無符號Laplace特征多項式QG(λ)為:

利用行列式行的初等變換,得到

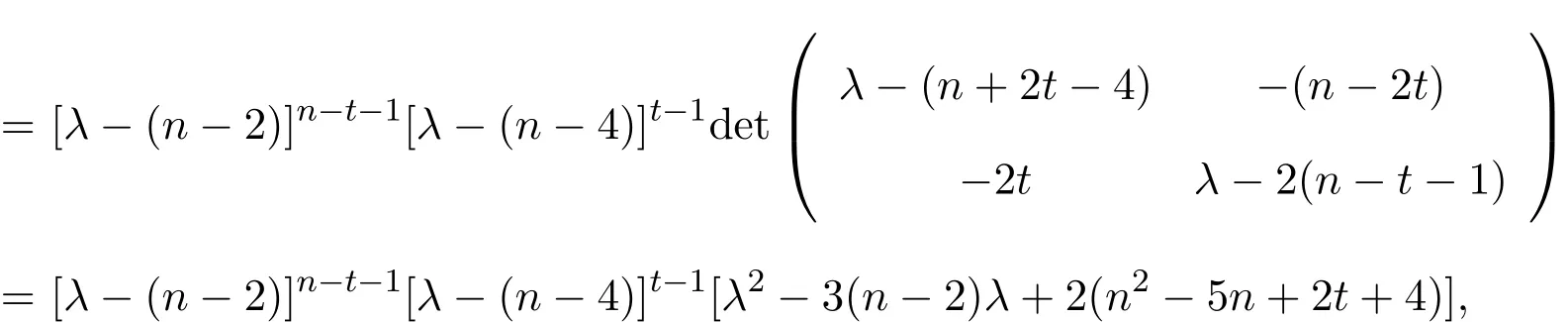

有整根.在n2+4n+4?16t和3(n?2)有相同的奇偶性的條件下,當且僅當n2+4n+4?16t是一個完全平方數時,方程有整根.

這里,當3(n?2)是偶數時,n是偶數.也是偶數.當3(n?2)是奇數時,n是奇數.也是奇數.


定理2.2設圖G=是具有n個頂點的完全圖Kn中刪去互不相鄰的條邊所得的圖類.




證明根據定理2.1得到圖G的無符號Laplace特征多項式QG(λ)為:

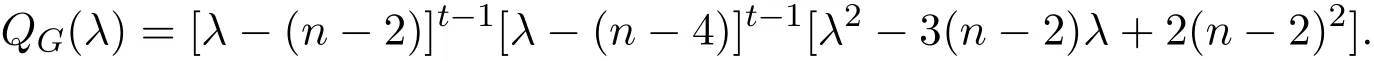

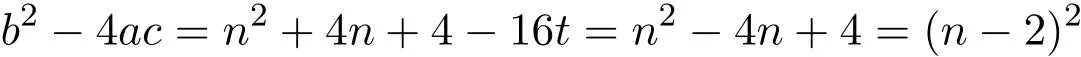


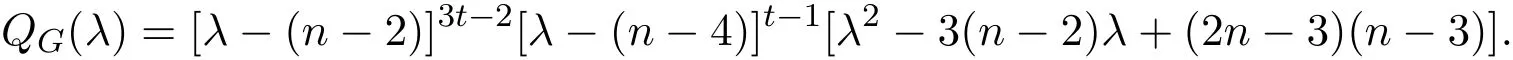




推論2.1設圖是具有n個頂點的完全圖Kn中刪去1條邊所得的圖類.則圖類K?k2n它的無符號Laplace特征多項式為:
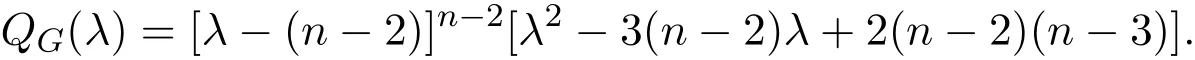
當n2+4n?12是平方數時,圖是Q整圖.
推論2.2設圖是具有n個頂點的完全圖Kn中刪去互不相鄰的2條邊所得的圖類.則圖它的無符號Laplace特征多項式為:
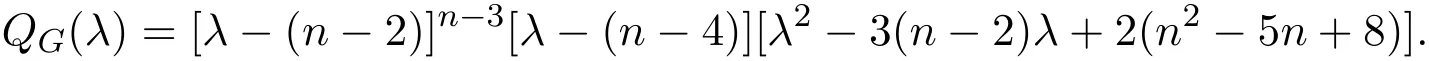
當n2+4n?28是平方數時,圖是Q整圖.
參考文獻
[1]Bondy J,Murty U S R.Graph Theory with Applications[M].New Youk:North-Holland,1976.
[2]Cvetovi′c D,Doob M,Sachs H.Spectra of Graphs Theory and Application[M].New York:Academic press, 1980.
[3]Harary F,Schwenk A J.Which graphs have integral[C]//Bari,Harary F.Graphs and Combinatorics.Berlin: Springer,1974.
[4]Balinska K T,Kupczyk M,Simic S K,et al.On Generating All Integral Graphs on 11 Vertices[R]//Science Center Report.Poznan:The Technical University of Poznan,2001.
[5]Wang Ligong,Liu Xiaodong.Integral complete multipartite graphs[J].Discrete Math.,2008,308:3860-3870.
[6]趙寧,吳廷增,郭承志.完全6-部圖是S-整圖的一個充分必要條件[J].純粹數學與應用數學,2013,29(2):132-139.
[7]盧世芳.完全4-部圖的無符號Laplacian整根[J].青海大學學報:自然科學版,2009,27(6):46-48,83.
[8]Lu Shifang,Zhao Haixing.Signless Laplacian characteristic polynomials of complete multipartite Graphs[J].數學季刊,2012,27(1):36-40.
[9]盧世芳,衛良,趙海興.完全3-部圖的無符號Laplacian譜[J].山東大學學報,2012(12):41-47.
[10]盧世芳.s=4的完全多部圖Ka1n1,a2n2,………,asns的無符號Laplace特征多項式[J].價值工程,2012(7):12-13.
2010 MSC:05C78
中圖分類號:O157.5
文獻標識碼:A
文章編號:1008-5513(2014)03-0229-05
DOI:10.3969/j.issn.1008-5513.2014.03.002
收稿日期:2013-12-01.
基金項目:教育部春暉計劃項目(Z2012091);青海大學中青年科研基金(2011-QGY-8).
作者簡介:盧世芳(1970-),碩士,副教授,研究方向:圖論.
Some new families of Q-integral graphs
Lu Shifang
(Department of Basic Research,Qinghai University,Xining810016,China)
Abstract:Based on the results of integral graphs,L-integral graphs and S-integral graphs.Characterized some new families of Q-integral graphs.We fi rstly give the necessary and sufficient condition for the graphs?to be Q-integral.Using the elementary row transformation of a matrix and the signless Laplace characteristic polynomial of the graphs?.Furthemore,we obtain large families of Q-integral graphs and their spectra.
Key words:signless Laplace spectra,signless Laplace characteristic polynomial,Q-integral polynomials

