一類非線性系統的周期擾動Hopf分支
殷紅燕
(中南民族大學數學與統計學學院,湖北武漢430074)
一類非線性系統的周期擾動Hopf分支
殷紅燕
(中南民族大學數學與統計學學院,湖北武漢430074)
研究了小周期擾動對一類存在Hopf分支的非線性系統的影響.特別是應用平均法討論了擾動頻率與Hopf分支固有頻率在共振及二階次調和共振的情形周期解分支的存在性.表明了在某些參數區域內,系統存在調和解分支和次調和解分支,并進一步討論了二階次調和分支周期解的穩定性.
Hopf分支;平均法;調和解分支;次調和解分支;穩定性
1 引言
周期擾動分支所考慮的問題是:當一個非線性動力系統正在經歷著某種分支狀態時,給它加上小周期擾動,研究其變化情況.其中周期擾動Hopf分支尤為引起人們的興趣.文獻[1-3]主要應用多重尺度法研究了周期擾動對一個分支系統的影響,文獻[4]用更替法對此類問題進行了研究.文獻[5]使用規范型及平均法研究了周期擾動Hopf分支問題的首次分支與二次分支現象.平均法是研究含小參數周期系統解的性質的一種比較方便簡捷的方法,此方法不僅用于研究常微分方程的周期擾動Hopf分支,還可用來研究滯后型泛函微分方程,相關結果可見文獻[6-7].本文主要使用平均法對常微分方程中的一類非線性系統的周期擾動Hopf分支情況進行研究,詳細給出了分支周期解存在的參數區域,并表明在不同的參數范圍內存在的周期解的個數是不同的.
所研究的系統為:
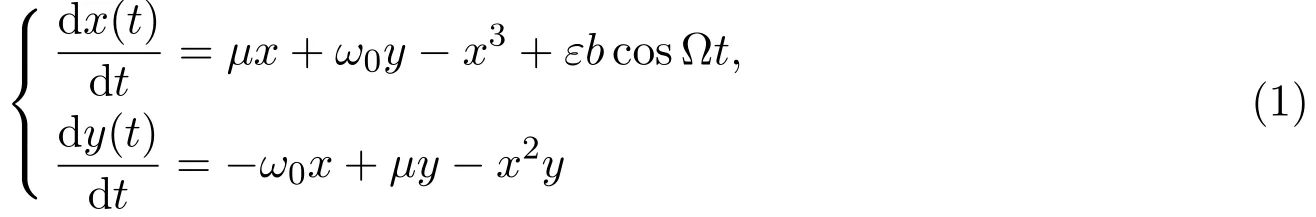
和
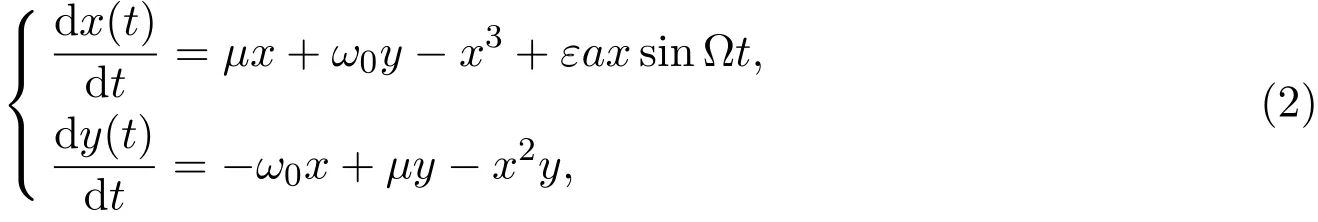
這里μ是分支參數,ε,a,b是實的參數,并且0<ε?1,進一步,引進一個去諧參數η,它由等式?=ω(1?η)所定義.
當ε=0時,系統(1)和(2)為:
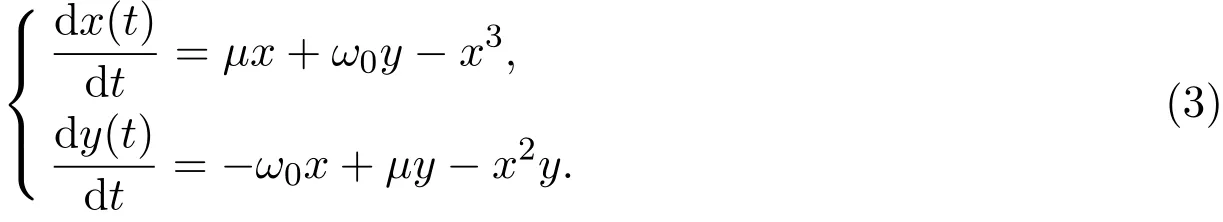
當μ=0時,系統(3)以(0,0)為唯一的平衡點,平衡點是中心型的,且容易驗證此平衡點是穩定的,當μ>0時,系統(3)以(0,0)為不穩定焦點.因此,當ε=0時,系統(1)和(2)在μ=0時存在Hopf分支,且分支發生在μ>0方向(上臨界),并且分支周期解是穩定的.
在第二節中,研究系統(1)在ε/=0的情形.主要討論周期擾動頻率?接近于臨界固有Hopf分支頻率ω0的情形.表明在某些參數范圍內,系統(1)存在調和解分支,并且隨著參數的變化,分支周期解的個數也會發生變化.
在第三節中,討論系統(2)在ε/=0的情形.主要討論周期擾動頻率?接近于臨界固有Hopf分支頻率ω0在二階次調和共振的情形.表明在某些參數范圍內,系統(2)存在次調和解分支,并且討論了次調和解的穩定性.
2 調和解分支
首先,對系統(1)進行尺度變換,令

則系統(1)化為:

再引入新的時間變量τ=?t,做變換
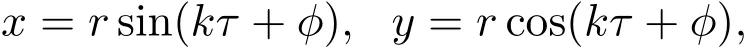
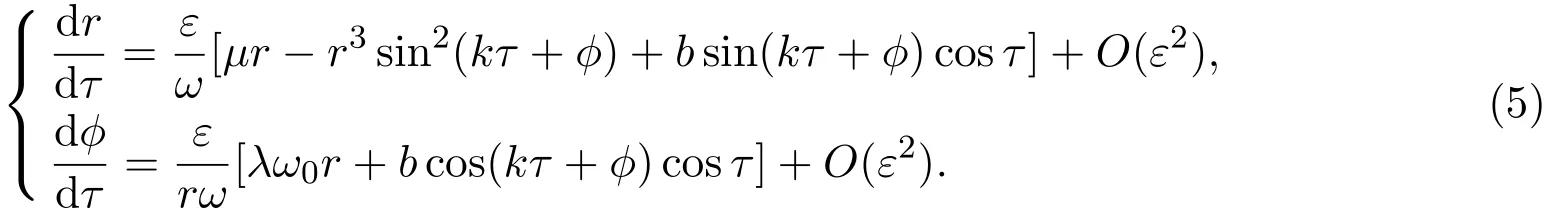
下面討論k=1的情形(共振情形),忽略O(ε2)項,對(5)式進行積分平均得到:
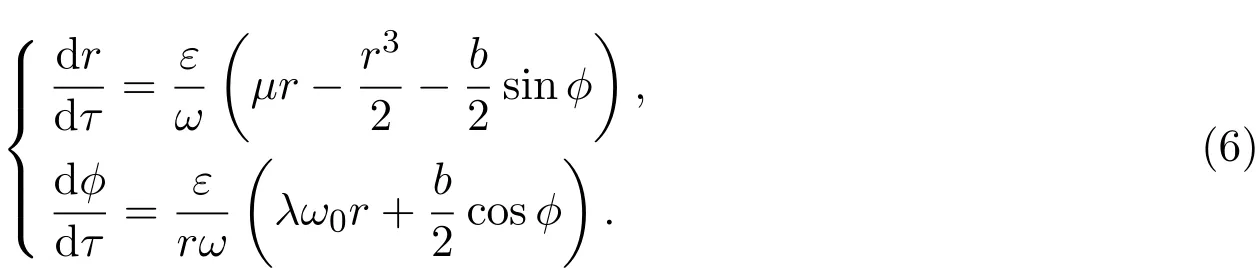
由平均定理[8],系統(6)的非平凡常數解對應于系統(4)的周期解.在系統(6)中令解得r所滿足的方程為:
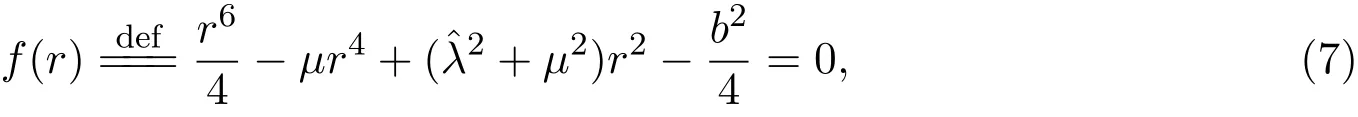
1.當μ2?32≤0時,對任意b2>0,方程只有一個正實根(包含有三重根情形).
2.當μ2?32>0,μ>0時,若b2∈C0,則方程(7)恰有三個正實根;若b2∈?C,則方程(7)恰有兩個正實根(其中有一個是二重根);若b2∈CC,則方程(7)只有一個正實根.這里C={x∈R|0 這樣就得到了: 定理2.1若系統(1)的參數μ>0,且那么當ε充分小時系統(1)存在調和解分支,而且調和解的個數隨著參數b的變化而不同. 對系統(2)進行尺度變換,令 則系統(2)化為: 由方程(10)可看出其正根的分布情況: 1.當時,方程(10)有兩個正實根,從方程(10)中可求得這兩個正實根為: 2.當時,方程(10)只有一個正根,取(11)式中符號為正的. 下面來考慮非平凡解的穩定性.令r=r0+ν1,?=?0+ν2,得到關于非平凡解的線性變分 方程為: 設方程(12)有形如exp(ρετ/ω)的解,那么ρ所滿足的特征方程為: 容易看出,當條件P(1)成立時,系統(9)的兩個非平凡解中, 是穩定的,而 是不穩定的.當條件P(2)成立時,若a>0,則系統(9)唯一的非平凡解為此解是穩定的;若a<0,則系統(9)唯一的非平凡解為此解是不穩定的.于是得到如下結論: 定理3.1若系統(2)的參數μ>0,且μ=O(ε),η=O(ε),那么當ε充分小時系統(2)存在二階次調和解.且當條件P(1)成立時,系統(2)存在兩個次調和解,其中一個為穩定的,一個為不穩定的.當條件P(2)成立時,若a>0,則系統(2)存在唯一的穩定的次調和解;若a<0,則系統(2)存在唯一的不穩定的次調和解. 參考文獻 [1]Rosenblat S,Cohen D S.Periodically perturbed bifurcation.I.Simple bifurcation[J].Stud.Appl.Math., 1980,63:1-23. [2]Rosenblat S,Cohen D S.Periodically perturbed bifurcation.II.Hopf bifurcation[J].Stud.Appl.Math., 1981,64:143-175. [3]Kath W L.Resonance in periodically perturbed Hopf bifurcation[J].Stud.Appl.Math.,1981,65:95-112. [4]Bajaj A K.Resonant parametric perturbations of the Hopf bifurcation[J].J.Math.Anal.Appl.,1986, 115:214-224. [5]Namachchivaya N S,Ariaratnam S T.Periodically perturbed Hopf bifurcation[J].Siam.J.Appl.Math., 1987,47:15-39. [6]殷紅燕,陳作清,胡智全.周期擾動對具有限時滯Lienard方程的Hopf分支的影響[J].華中師范大學學報:自然科學版,2010,44(3):361-364. [7]呂堂紅,周林華.一類物價瑞利模型在小周期擾動下的Hopf分支[J].揚州大學學報:自然科學版,2012, 15(4):20-24. [8]韓茂安.動力系統的周期解與分支理論[M].北京:科學出版社,2002. Periodically perturbed Hopf bifurcation of a kind of nonlinear systems Yin Hongyan The in fl uence of small periodic perturbations on a kind of nonlinear systems exhibiting Hopf bifurcation is studied.In particular,we discuss the existence of bifurcating periodic solutions in the case that the excitation frequency and the critical natural frequency of Hopf bifurcation is resonance and subharmonic resonance.In this work,the ideas related method of averaging.It is shown that in some parameter regions the systems exhibit harmonic solution bifurcation and subharmonic solution bifurcation.Furthermore,the stability of subharmonic solutions is discussed. Hopf bifurcation,method of averaging,harmonic solution bifurcation, subharmonic solution bifurcation,stability O175 A 1008-5513(2014)03-0240-05 10.3969/j.issn.1008-5513.2014.03.004 2014-02-28. 中央高?;究蒲袠I務費專項資金(CZQ13016). 殷紅燕(1978-),碩士,講師,研究方向:微分方程定性理論. 2010 MSC:34C233 次調和解分支和穩定性
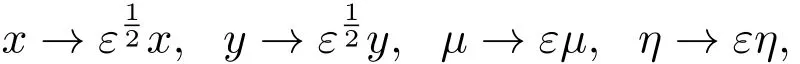
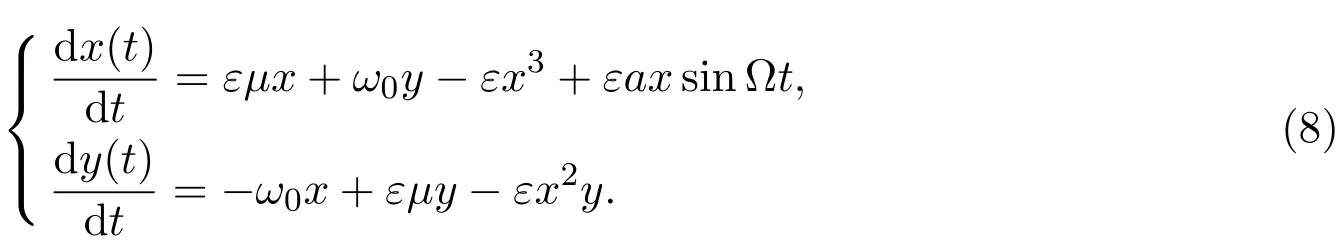
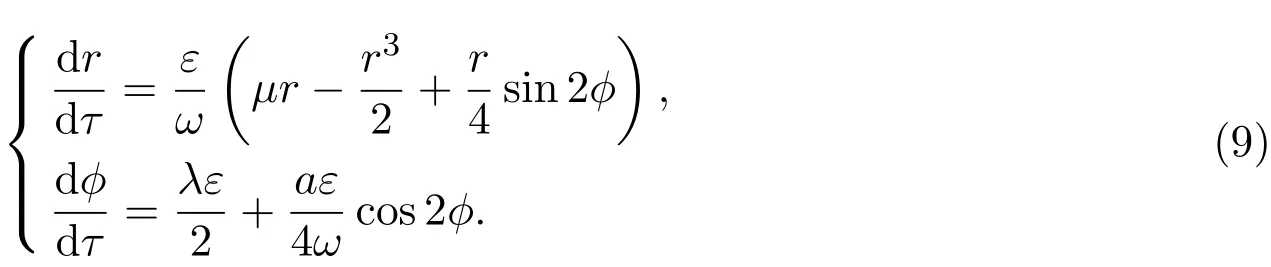
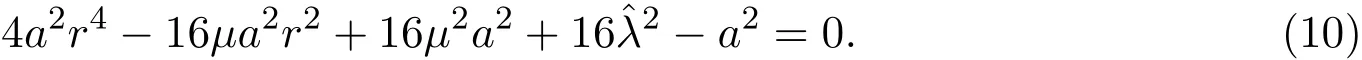
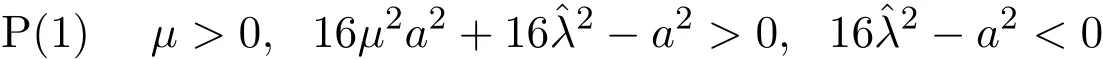
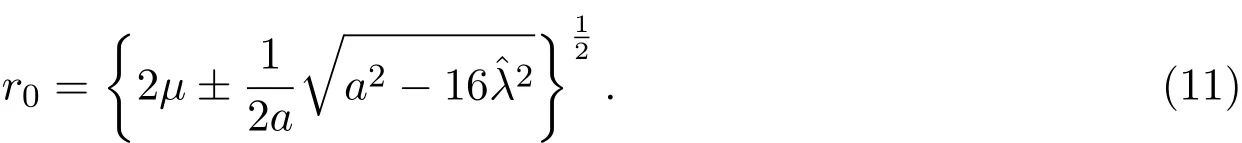
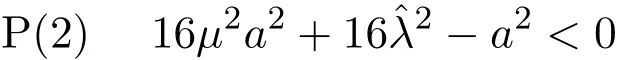
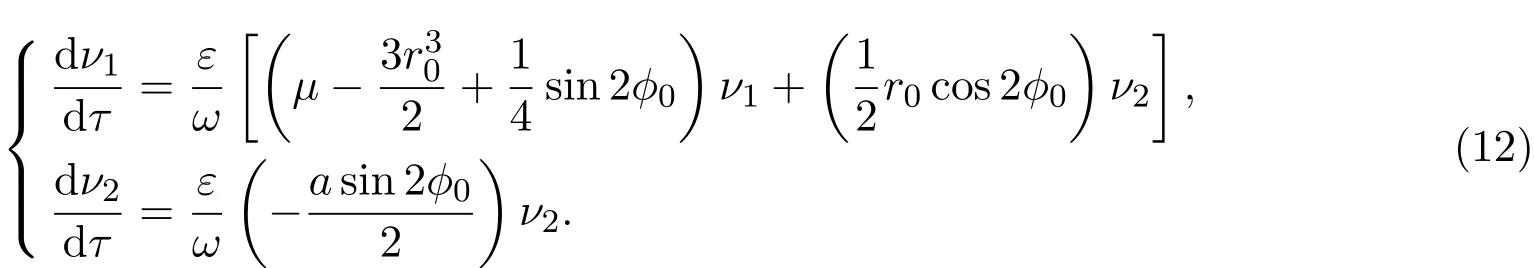

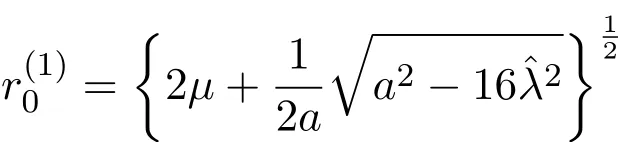
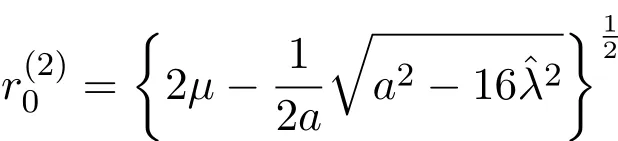
(College of Mathematics and Statistics,South-Central University for Nationalities, Wuhan430074,China)

