兩類圖的符號控制數

任媛,趙凌琪,吉日木圖,王妍

(1.內蒙古民族大學數學學院,內蒙古通遼市028043; 2.內蒙古民族大學計算機科學與技術學院，內蒙古通遼市028043; 3.山東水利職業學院信息工程系,山東日照276826)

兩類圖的符號控制數

任媛1,趙凌琪2,吉日木圖1,王妍3

(1.內蒙古民族大學數學學院,內蒙古通遼市028043; 2.內蒙古民族大學計算機科學與技術學院，內蒙古通遼市028043; 3.山東水利職業學院信息工程系,山東日照276826)

圖G的符號控制數(G)有著許多重要的應用背景,因而確定其精確值有重要意義.Cm表示m個頂點的圈,n?Cm和n…Cm分別表示恰有一條公共邊或一個公共頂點的n個Cm的拷貝.給出了n?Cm和n…Cm的符號控制數.

圖;符號控制函數;符號控制數

1 引言

本文中所指的圖均為無向簡單圖,文中未說明的符號和術語同文獻[1].

近些年來,圖的控制理論的研究越來越廣泛,各種控制概念相繼產生,例如符號邊控制,符號邊全控制,減控制,弱符號控制,符號星K控制等等,并獲得了一些初步的研究成果[2-6],尤其是對圖的符號控制,得到了許多新的結論[7-11].設圖G=(V,E).v∈V,v的開鄰域是與v相鄰接的頂點集合,即N(v)={u|uv∈E}.稱N(v)∪{v}為v的閉鄰域,記為N[v].

定義1.1[7]圖G=(V,E)的頂點集V上,定義一個雙值函數f:V→{?1,+1},并且f[v]=f(N[v]),若在任何一個頂點v的閉鄰域N[v]上函數值的和至少是1,即?v∈V, f(N[v])≥1,則稱函數f是G的一個符號控制函數.一個符號控制函數的權重是

圖G的符號控制數γs(G)定義為γs(G)=min{f(V)|f是G的符號控制函數}.

定理1.1[7]對階為n≥3的圈圖

定理1.2[7]對完全圖Kn,有

定理1.3[7]星圖K1,m的符號控制數γs(K1,m)=m+1.

對二部圖Km,n(n≥m≥2),有下面兩個定理:

定理1.4[7]當m=2,3時,有

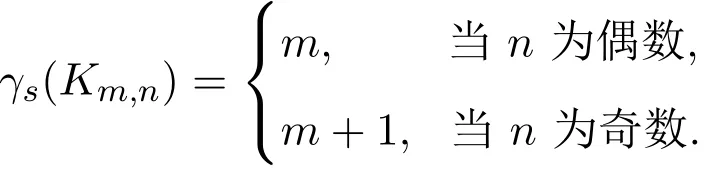
定理1.5[7]當n≥m≥4時,有

定理1.6[8]對任意正整數n≥2,扇圖

定理1.7[8]對任意正整數n≥3,輪圖

定理1.8[9]對于任意n階圖G,?和δ分別為圖G的最大度和最小度,則有

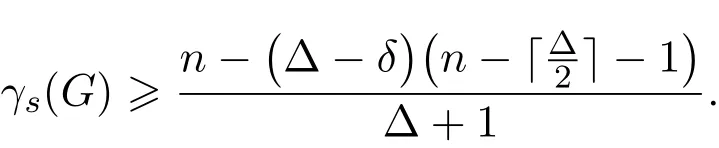
本文給出了n?Cm和n…Cm的符號控制數.

2 主要結果

定理2.1對任意正整數m≥3,n≥2,有

證明令表示n?Cm中的第i個m-圈,u和v表示的兩個公共頂點,n?Cm中的第i個m-圈中余下的頂點依次為

設函數f是n?Cm的一個符號控制函數,注意到:

下面分三種情況進行討論.

情況1當m≡0(mod 3)時,考慮u和v的對稱性,只需討論下面三種情況.

情況1.1當f(u)=f(v)=?1時.

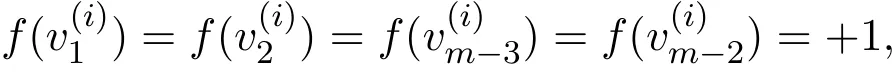
當m=3時,不滿足符號控制函數的定義,故下面考慮m>3時,由

容易得到每個m-圈中余下(m?6)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?6)個頂點中分配值為?1的個數為時,下面給出此時的一個符號控制函數:

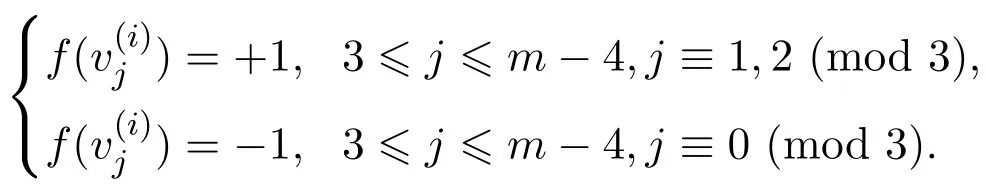
情況1.2當f(u)=?1,f(v)=+1時.

容易得到每個m-圈中余下(m?4)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?4)個頂點中分配值為?1的個數為時,下面給出此時的一個符號控制函數:

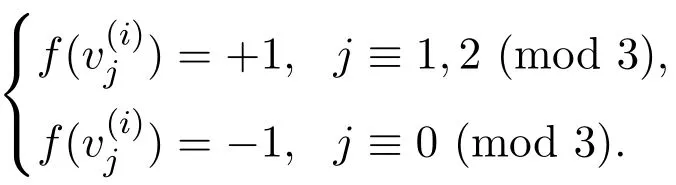
情況1.3當f(u)=f(v)=+1時.

下面討論n?Cm(m≡0(mod 3))中滿足上述條件的的個數:

由

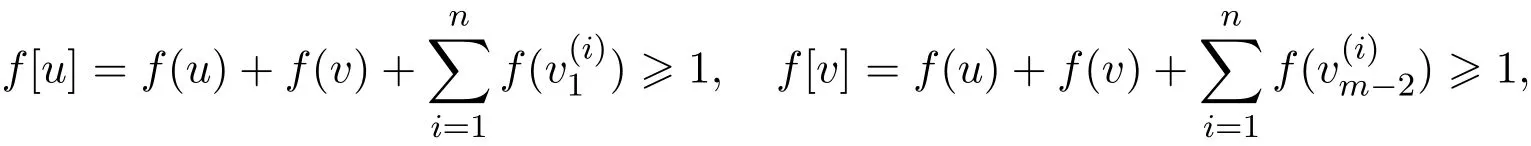
此時,f是滿足要求的、權最小的一個符號控制函數.

情況1.3.1當n≡1(mod 2)時,此時

情況1.3.2當n≡0(mod 2)時,此時

結合情況1.1,情況1.2,情況1.3,有

其中m≡0(mod 3).

情況2當m≡1(mod 3)時,考慮u和v的對稱性,只需討論下面三種情況.

情況2.1當f(u)=f(v)=?1時.

用情況1.1中同樣的方法,容易得到每個m-圈中余下(m?6)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?6)個頂點中分配值為?1的個數為時,下面給出此時的一個符號控制函數:

情況2.2當f(u)=?1,f(v)=+1時.

情況2.3當f(u)=f(v)=+1時.

結合情況2.1,情況2.2,情況2.3,有

情況3當m≡2(mod 3)時,考慮u和v的對稱性,只需討論下面三種情況.

情況3.1當f(u)=f(v)=?1時.

情況3.2當f(u)=?1,f(v)=+1時.

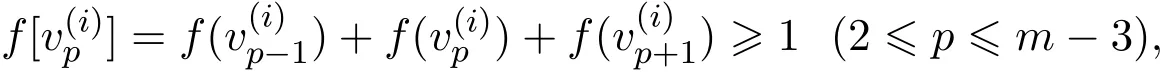
容易得到每個m-圈中余下(m?5)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?5)個頂點中分配值為?1的個數為時,又由

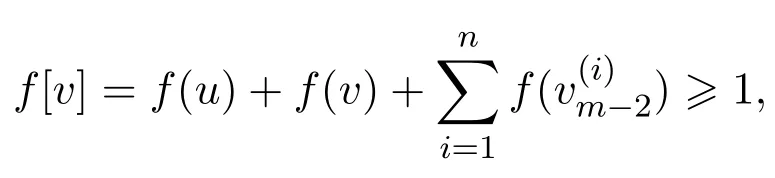
此時,f是滿足要求的、權最小的一個符號控制函數.

情況3.2.1當n≡1(mod 2)時,此時

情況3.2.2當n≡0(mod 2)時,此時

情況3.3當f(u)=f(v)=+1時.

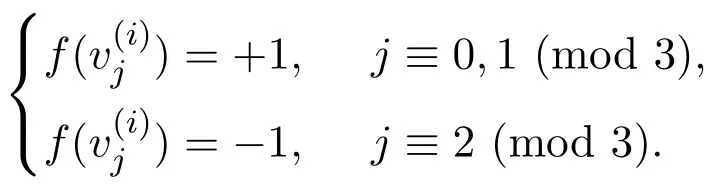
結合情況3.1,情況3.2,情況3.3,有

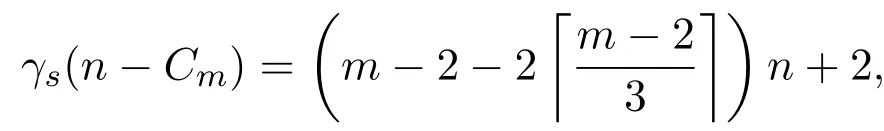
其中m≡2(mod 3).

綜上所述,對任意正整數m≥3,n≥2,

定理2.2對任意正整數m≥3,n≥2,

證明令表示n…Cm中的第i個m-圈,u表示的公共頂點,n…Cm中的第i個m-圈中余下的頂點依次為

設函數f是n…Cm的一個符號控制函數,注意到:

下面分三種情況進行討論:

情況1當m≡0(mod 3)時.

下面給出此時的一個符號控制函數:

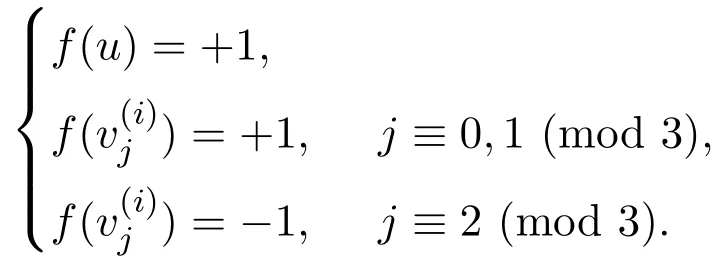
情況2當m≡1(mod 3)時.

情況2.1當f(u)=?1時.

容易得到每個m-圈中余下(m?5)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?5)個頂點中分配值為?1的個數為時,下面給出此時的一個符號控制函數:

情況2.2當f(u)=+1時.

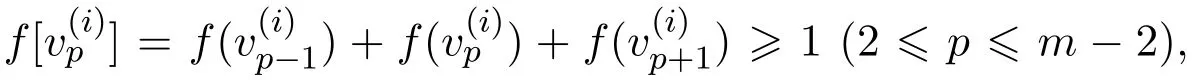
由容易得到每個m-圈中余下(m?1)個頂點中分配值為?1的個數最多為現在考慮每個m-圈中余下(m?1)個頂點中分配值為?1的個數為時,下面給出此時的一個符號控制函數:

結合情況2.1,情況2.2,有

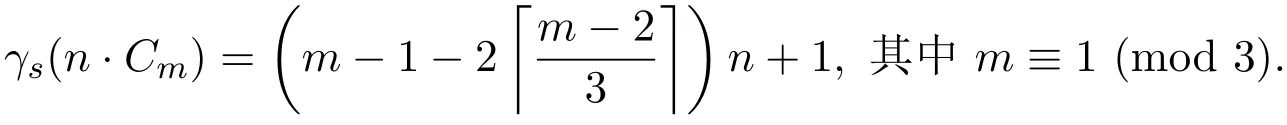
情況3當m≡2(mod 3)時.

情況3.1當f(u)=?1時.

情況3.2當f(u)=+1時.

下面討論n…Cm(m≡2(mod 3))中滿足上述條件的的個數:

由

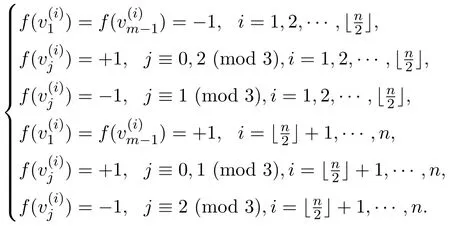
此時,f是滿足要求的、權最小的一個符號控制函數.

情況3.2.1當n≡1(mod 2)時,此時

情況3.2.2當n≡0(mod 2)時,此時

結合情況3.1,情況3.2,有

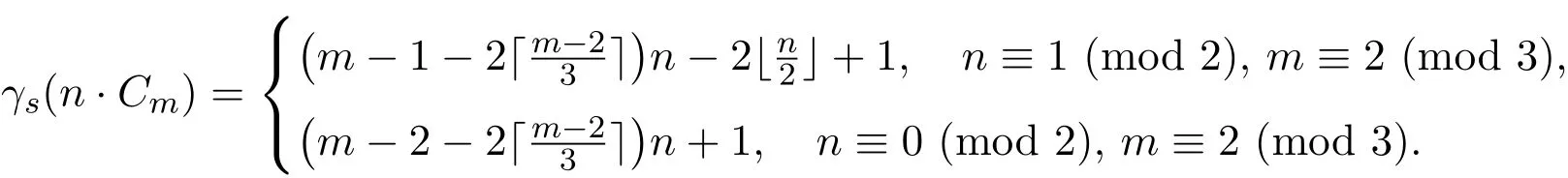
綜上所述,對任意正整數m≥3,n≥2,

[1]Bondy J A,Murty U S R.Graph Theory With Applications[M].London:Macmillan,1977.

[2]Xu Baogen.On signed edge domination numbers of graphs[J].Discrete Math.,2001,239:179-189.

[3]Zhao Jinfeng,Xu Baogen.On signed edge total domination numbers of graphs[J].Journal of Mathematical Research Exposition,2011,31(2):209-214.

[4]Xu Baogen.On minus domination and signed domination in graphs[J].J.Math.Res.Exposition, 2003,23(4):586-590.

[5]尚華輝,苗連英,苗正科,等.關于圖的弱符號控制數的下界[J].純粹數學與應用數學,2010,26(4):691-695.

[6]李春華.圖的符號星K控制數[J].純粹數學與應用數學,2009,25(4):638-641.

[7]于崇智,徐保根.圖的符號控制數[J].華東交通大學學報,1997,14(4):54-58,67.

[8]于崇智.圖的最小符號控制函數的充要條件[J].陰山學刊,1999,15(1):5-8.

[9]徐保根,丁宗鵬,羅茜.圖的符號控制數的下界[J].華東交通大學學報,2011,28(3):69-72.

[10]王軍秀.特殊圖類的符號控制數[J].純粹數學與應用數學,2005,21(1):59-61.

[11]徐保根.圖的控制理論[M].北京:科學出版社,2008.

Signed domination numbers for two class of graphs

Ren Yuan1,Zhao Lingqi2,Jirimutu1,Wang Yan3
(1.College of Mathematics,Inner Mongolia University for Nationalities,Tongliao028043,China; 2.College of Computer and Technology,Inner Mongolia University for Nationalities,Tongliao028043,China; 3.Department of Information Engineering,Shandong Water Polytechnic,Rizhao276826,China)

The signed domination number of a graph has its import and applying background,so it is useful to determinate the exact value of it.Cmdenotes the cycle of length m,n?Cmand n…Cmdenote the graph obtained from any n copies of Cmwhich have just one common edge and one common vertex,respectively.In this paper,we obtain the signed domination numbers of n?Cmand n…Cm.

graph,signed domination function,signed domination number

O157.5

A

1008-5513(2014)03-0271-09

10.3969/j.issn.1008-5513.2014.03.008

2012-06-07.

國家自然科學基金(61261025,61262018);內蒙古民族大學校級研究項目(NMD1104).

任媛(1987-),碩士,助教,研究方向：圖論及其應用.

2010 MSC:05C78