數學教師糾錯教學策略研究*
——從處理學生解題錯誤談起

陳建華 文 清

(1.揚州大學 江蘇揚州 225002； 2.成都大學 四川成都 610106)

數學教師糾錯教學策略研究*
——從處理學生解題錯誤談起

陳建華1文 清2

(1.揚州大學 江蘇揚州 225002； 2.成都大學 四川成都 610106)

教師的學科知識不能自動地產生成功的教學方式和教學理念；缺乏堅固的學科支撐，成功的教學方式和新穎的教學理念不可能實現。為了支持學生更深入學習高等數學，教師應該不斷積累、完善自己的數學教學知識結構，聚焦課堂教學實踐與反思，走向開拓性教學。通過教師對學生產生解題錯誤的不同教學處理，考察教師糾錯教學策略。借助習題涉及教學內容的知識包，探討數學教師掌握教學內容知識的深度、廣度對教學的影響，以及數學教師糾錯教學策略。

數學教師；糾錯教學策略；矩陣；零因子；秩；線性方程組；知識包

線性代數內容抽象，知識點間聯系緊密。它在給學生提供數學思維訓練素材的同時，也給學生理解課程的概念和法則甚至計算都帶來困難，亦給教師的教學帶來難度。基于課堂教學實踐的訪談，也是評價教師知識常見的方法之一[1]。本文通過教師對學生解題錯誤的不同教學處理，了解任課教師對線性代數糾錯教學能力的現狀。借助相關教學內容的知識包，討論數學教師掌握教學內容知識的深廣度對教學的影響，以及數學教師學科水平與教學能力契合的發展方向。

一、一道線性代數試題引出的話題

(一)從學期考試中獲得的問題情境

這是一道貌似簡單實質蘊含深刻的智慧的檢測學生矩陣的概念、計算等及相關知識聯系教學的有價值的題目，既考查學生基礎知識又考查其分析、解決問題的能力，還考查其嚴謹治學的意識。

2013年1月，將上題作為一道解答題植入線性代數課程期末試卷，為了保證測試調查的真實性、有效性，將其編排在試卷的前半部分。閱卷后，隨機選取兩個班級，進行了答題情況統計。結果如下：學生人數72人(不考慮重修學生)，未做解答的5人，獲得結論“k=-3”的65人中，理由正確的有36人，理由不正確的有29人。不正確的推理過程主要有兩類：

錯解(1)：因為AB=O，且B≠O，所以A=O，故行列式|A|=0。

錯解(2)：因為AB=O，所以|A|·|B|=0，由于B≠O,故|B|≠0，從而行列式|A|=0。

(二)從問題情境中引出的話題

請您花點時間考慮一下：如果您的學生發生上述錯誤，您認為：學生產生錯誤的原因是什么？教學中怎樣幫助學生改正錯誤？

(三)討論話題的對象

本年度講授過線性代數課程的大學數學教師，共18人。為了敘述方便用教師姓名拼音首字母代替某教師，其中新教師(教齡4年以下，用N表示)6人，經驗型教師(教齡4年以上)12人。本科學歷1人，碩士學歷4人，博士學歷(用D表示)13人；具有代數知識背景(攻讀碩士、博士階段是基礎數學代數方向，用A表示)的6人；具有教學知識背景(即本科階段是師范專業，用T表示)的12人。

二、學生解題錯誤成因與教學策略的討論

本研究中的所有教師都認為，學生在進行矩陣乘法的運算中用錯了運算律， 行列式和矩陣概念理解出現了問題。然而，他們在解釋學生解題出錯原因和如何幫助學生改正該錯誤時表達了不同的見解。

(一)學生解題錯誤成因討論

新教師在討論學生的錯誤時，6位教師都認為錯解(1)是由于學生對矩陣的乘法理解不深刻。錯解(2)是將零矩陣和矩陣的行列式為零兩個概念混淆了。在解釋學生的錯誤的過程時，雖然，ZJW(DN)是新教師，但她的分析還是簡潔明了的：

矩陣的乘法運算中存在零因子，即兩非零矩陣的乘積可能為零矩陣，部分學生形成錯解(1)，是由于對此疏忽造成的。我們可以通過一些例子來提醒學生注意，比如可以給學生下列例子：

另外5位新教師，也像ZJW這樣，雖然提及“零因子”或“方陣的行列式”，但他們沒有給學生提供反例，或告訴學生閱讀教材的相應部分，讓學生關注基本概念或運算律。關于解題的思維過程，一位新教師認為從解題的角度看，要求k值，當然只有|A|=0，才能推出具體數值。他認為學生不必過多糾纏“為什么”，傾向于讓學生記憶其思維模塊。由此可以看出，這些教師未想到要促進學生對矩陣乘法運算的深入理解，明晰混淆的概念；僅僅是從解題需要出發，建議學生如何做題。雖然他們的教學法理解有概念性理解的傾向，但還是處于過程性理解階段[2]。

雖然經驗型教師解釋學生的錯誤總體而言與新教師有相同之處，但他們更期望學生能夠學會更多而不僅僅是例子，希望學生學會在這個運算法則下所蘊含的數學原理。概念組的教師關注矩陣運算系統和實數運算系統，指出矩陣與行列式的本質區別，能提醒學生從函數的角度，理解方陣行列式的聯系。如JRZ(DAT)給出解釋是：

矩陣代數系統Mn(R)與我們熟悉的實數系統R的本質區別是在Mn(R)中存在零因子，消去律不成立，而實數系統中不存在零因子。我會給學生一個對照表，將矩陣系統和實數系統作一個比較，讓學生區分兩個系統，以加深對問題的理解。

實數集合R矩陣集合Mn(R)結合律、分配律結合律、分配律交換律、消去律零因子元素a可逆?存在b使得ab=ba=1?a≠0?存在b使得ab=1元素A可逆?存在B使得AB=BA=EA?|A|≠0?存在B使得AB=E

關于a≠0與|A|≠0從代數角度抽象地看，二者無任何差別。雖然矩陣的記號(數表外加括號)與行列式記號(數表外加兩豎線)很相像，但它們是兩個截然不同的概念，行列式是一個數，而矩陣為一個矩形的數列表。一方面，只有方陣才可能取行列式；另一方面，方陣與它的行列式又是密切相關的，行列式是方陣特性的重要標志，提高一個層面看，可以把矩陣(對應于一個數)看成方陣的函數。

事實上，對任意的A∈Mn(R)，如何定義其函數值f(A)，在不同的領域有多種不同的回答，矩陣A對應于|A|只是其中一種意義深刻的對應方法，比如行列式是否為零，把矩陣劃分為奇異和非奇異兩類。當我們將方陣的行列式概念推廣為矩陣的行列式的概念后，可以揭示出矩陣更深刻的特性，人們通常認為方陣的行列式概念是講授矩陣秩的先導。所有這些充分傳達了教師們對課題的概念性理解，對方陣行列式的核心思想的把握。

一部分有教學法知識背景的教師對學生的錯誤的解釋表現出特定的視角。他們認為：從學生的學習過程看，學生發生這兩類錯誤的根本原因是“存在矩陣B≠O”抽象造成的。如果題目中矩陣是具體給出的，學生的求解不就是剩下矩陣的乘法運算了嗎?應該從“存在矩陣B≠O”的作用是什么開始考慮問題：一個元素不為零、一列向量不為零或整個矩陣不為零，它們又能聯系哪些相關知識點或結論呢？面對有44.62%的學生就此題出現錯誤的現象，說明這是幫助學生正確運用矩陣運算律、辨別矩陣與行列式概念的極好素材。教學中要好好利用這一寶貴教學資源，達到“留得殘荷聽雨聲的”教學效果。

(二)糾錯教學策略討論

兩組教師對學生的錯誤的解釋不同，同樣處理學生錯誤的策略也有不同的方法。兩位新教師認為，之所以出錯是學生沒有很好地利用矩陣分塊的技巧，如果學生能夠想到將矩陣分塊B=(β1，β2，β3)，則有AB=(Aβ1,Aβ2,Aβ3)=O，自然會聯系齊次線性方程組AX=0。這兩位教師用語言說明了推理過程和步驟。

與新教師的“大框架”給學生提供問題思路的指導不同的是，經驗型教師的指導顯得更細致，他們希望學生清楚每一步推導的理由。如SHC(T)是一位從事大學數學教學二十多年的老教師，他認為必須給學生詳細的解題過程指導：

記B=(β1,β2，β3)，則AB=O?A(β1,β2，β3)=O(將矩陣B作列分塊)?(Aβ1,Aβ2,Aβ3)=O(分塊矩陣的乘法運算)?Aβ1=O(i=1,2,3)(分塊矩陣的相等)?β1(i=1,2,3)是齊次齊次線性方程組AX=O的解。?AX=O有非零解(因為B≠O，所以存在βi≠0)?|A|=0。

對于如何恰當地利用分塊矩陣進行矩陣的乘法，使之便于運算或論證，這是一個復雜且技巧性很高的問題。雖然矩陣的列分塊方法是常見的分塊方法，但結合本文討論的問題，到底是如何聯系上的呢？筆者進行如下追問：“您為什么會想到對矩陣B做列分塊？”SHC(T)：“為什么？可能是長期教授該課程，好像見到AB=O，總能想到將矩陣B分塊，然后聯系上齊次線性方程組AX=0。”筆者：“如果對矩陣A做列分塊，能獲得解題思路嗎？”SHC(T)：“應該可以的吧，還沒考慮過。”

矩陣分塊法是矩陣計算中的一種技巧，其好處在于矩陣分塊后，能夠突出該矩陣的結構，從而可以利用它的特殊結構，使得運算簡化；除了將運算調理化外，還可以為某些命題的證明提供方法和思路。如將m×n矩陣進行分塊A=(α1,α2,…，αm)，那么，在運算中，它可以視為一個“向量”，這時矩陣等同于它的列向量組。由此，理解矩陣與向量組的關系，這是對矩陣概念的深化，也是后續內容中利用矩陣來討論向量組的基礎。

帶著某些特定的期望，筆者訪談了一位有代數背景的老教師SJH(DAT)。在介紹基本情況后，直接詢問他：“您是如何聯系齊次線性方程組的？您會怎樣給學生提供思考問題的策略？”他說：

題目條件“AB=O,B≠O”的本質是思考問題的關鍵，于是我們可以從B≠O仔細考慮。若B≠O理解為有一個元素不為零，則在AB=O中矩陣A與一個元素相乘不好解釋，所以接著從該非零元素所在的列不為零考慮，則有Aβ=O，且β≠O，這樣克萊姆法則的結論自然聯系上。

SJH(DAT)稍稍思考后接著說：

若B≠O，從矩陣的秩不為零(即R(B)≥1)考慮，由AB=O，知道R(A)+R(B)≤3，從而R(A)≤2，則有|A|=0。問題也得到解決。

教師期望學生所知道的與教師自己的知識是相關的，僅僅期望學生學會這個過程的教師，往往只有過程性的理解。同時，有限的學科知識限制了教師促進學生概念學習能力的培養。一位長期從事碩士研究生入學輔導的教師WJC(DAT)，他給出的糾錯教學策略是：

此題思考的焦點是方陣的行列式，我認為中間結論|A|=0，應該可以猜測得到。而(非)奇異矩陣是線性代數中最重要和最基本的概念之一，沿著此思路，可以讓學生回憶刻劃|A|=0的等價條件，尋找解題思路。

根據WJC(DAT)的訪談整理得如下對照表：

|A|=0的等價條件解題思路AX=O有非零解將矩陣B作列分塊,由AB=O,B≠O判斷AX=O有非零解,故|A|=0A的秩小于3利用關系R(A)+R(B)≤3,且B≠O,從而R(A)≤2,故|A|=0A的列向量組線性相關將A做列分塊,A=(α1,α2,α3),由AB=O,B≠O,不妨令β=(k1,k2,k3)T≠0,則有k1α1+k2α2+k3α3=0,故A的列向量組線性相關,從而|A|=0A有特征值為零(|A|=λ1λ2λ3)由于B≠O,不妨令β為B的非零列向量,則由AB=O有Aβ=O=O·β,從而,矩陣有一個特征值為零,β是A的屬于0的特征向量,故|A|=0

教學實踐中，注重教學方法、關注學生學習過程的有3位教師，其中1人是教育學碩士，1人是課程與教學論方向博士。他們在學生出現錯誤的成因分析和糾錯教學策略指導中都能充分考慮學生學習習慣，有2位教師是采用反證法推導矩陣行列式|A|=0。QLL(T)教師認為：

從方法論的角度看，當我們正面思考問題受阻時，可以嘗試從反面考慮，假設矩陣A的行列式不為零，即|A|≠0，則它是可逆矩陣，在等式AB=O兩邊左乘A-1，則有A-1AB=A-1O，由此推出B=O與題設矛盾。

該思路簡潔明了，充分體現了“正難則反”的思維模式的威力。利用A-1這一具體對象交給將剛踏入全新矩陣運算系統的學生，避免了“無從著手，空中樓閣”的困惑。這里方法論知識對問題的解決發揮了決定性的作用。

課程與教學論方向博士ZBD(DT)的指導策略是為犯錯誤學生提供診斷性練習。她設計了幫助學生“診斷錯誤、解決問題”的一串練習題，試圖通過這些練習提出過程背后的概念性問題。

習題1 設非零矩陣

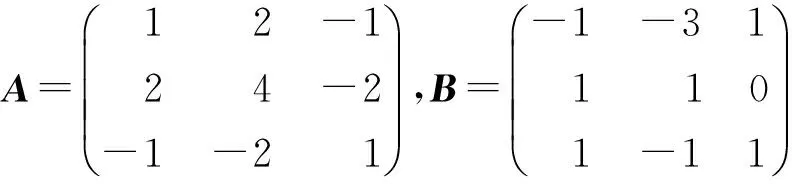
計算AB。由計算結果與題設條件比較，你發現了矩陣運算的什么特性？

計算矩陣的行列式|A|，思考零矩陣與矩陣行列式為零的區別與聯系。

分別求非零矩陣

使得AB=O，其中R(B1)=R(B2)=R(B3)=1。

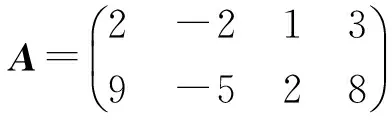
盡管這串習題從計算的角度看是從過程性方面開始的，但計算后的思考又讓學生回到概念，通過該習題串成功地幫助學生在理解的基礎上記住矩陣運算的若干規則。從教學角度看，既為學生指明思考問題的方向，又讓學生自己去發現錯誤、糾正錯誤。此外，教師們還提到一些基于學習的策略，如組織學生學習、幫助學生觀察、指導學生參與討論等。

三、學科知識與教學策略關系的討論

(一)知識包的建立和分析

綜合分析討論的過程，我們可以獲得關于本文所研究習題的一個知識包(圖1)。知識包中橢圓表示研究課題，圓角長方形表示相關知識點，通過有向線段聯系相關知識點；所有部分都明顯地與研究習題有關，知識包的下層支持對學生錯誤的解釋，上層則對教師給學生提供解題策略提供有力支持。

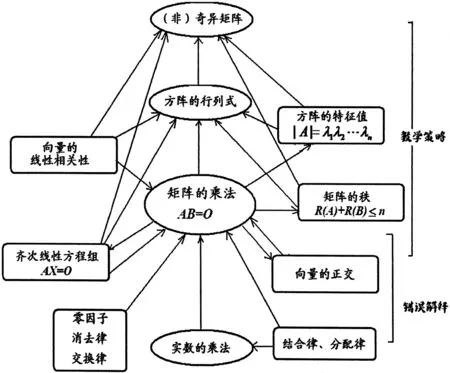
圖1 習題的知識包

知識包中的概念是濃縮的知識點，也是教學中師生思維的“細胞”。教學中可以從關鍵知識點，揭示其被掩蓋的特殊情況，如“矩陣B≠O”背后的“?bij≠O”或“?βj≠O”或“R(B)≥1”等，通過給出各種具體模式，幫助學生理解。也可以區分概念的異同，尋找它們的關鍵之處。

從學科知識的角度來看，參加討論的教師的知識理解幾乎都包含在這個包內。關于問題解決的教學策略，“奇異矩陣”幾乎是所有教師都能意識到的關鍵概念。大多數新教師考慮問題限制在解釋錯誤和解答問題范圍內。而經驗型教師，特別是有代數專業方向背景，或具有教學需求的教師(如SJH(DAT)和WJC(DAT))，能夠很“輕松”地從較多角度討論相關內容。這說明：專業知識背景的不同、教學知識的差異影響對知識包的相關各成分的了解范圍，導致教師教學策略的優劣。

(二)“概念性理解”并非簡單

新教師理解的深刻程度較淺，只能將知識包中少數元素引入問題的解決過程，且較為孤立。6位新教師中，關于錯誤解釋有2人在過程性理解層面，4人在概念性理解層面；從教學策略角度看，只有1位教師達到概念性取向。經驗型教師中，也只有具有代數背景的，或有教學需要的教師才有發展完全的、組織良好的概念性理解的知識包。統計表明：在12名經驗教師中，有10名(占83%)關于錯誤解釋在概念性理解層面；從教學策略角度看，只有8位教師達到概念性取向。圖2顯示了教師關于該內容的學科知識，圖3顯示了教師在認識和處理該問題時的教學法傾向。

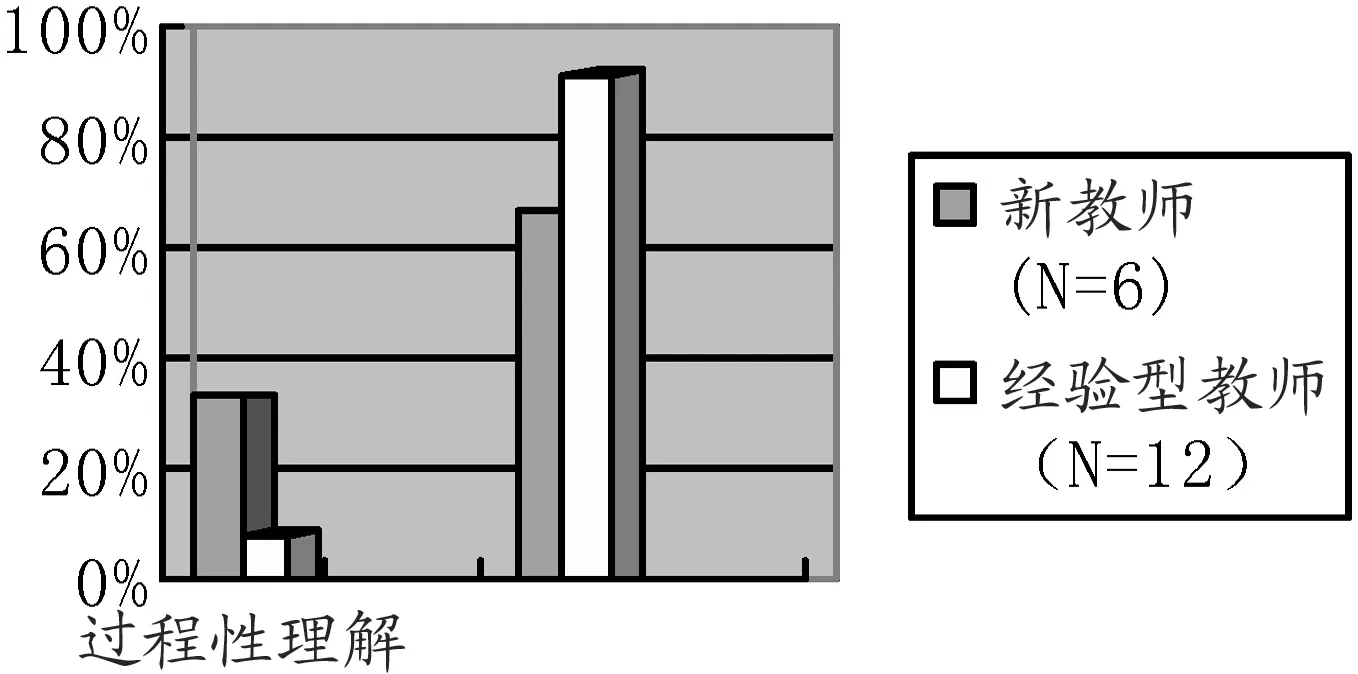
圖2

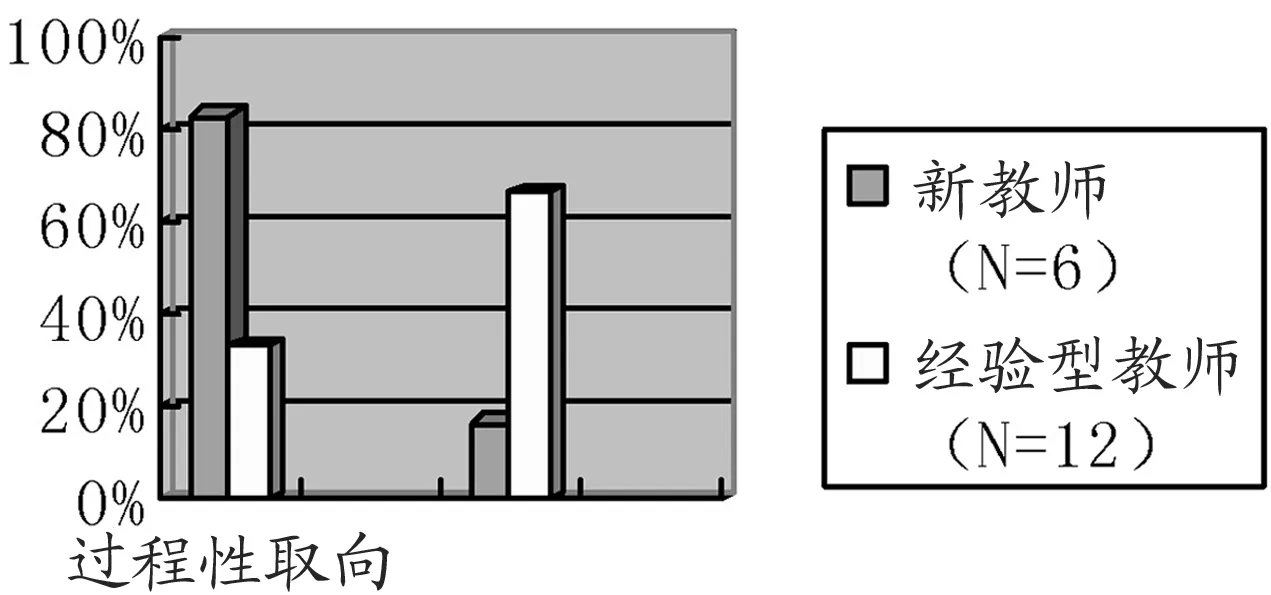
圖3

無論是新教師還是經驗型教師，從教學策略上看概念性取向的人數要比解釋錯誤時概念性理解的人數要少。這提示我們，數學知識的“概念性理解”并非簡單。訪談調查中，ZBD老師設計的習題串，從問題形式挖掘學生的思維過程，從學生的立場解釋知識、表征知識，能促進學生對數學知識的理解從過程性轉向概念性，給我們很好的啟示。

(三)若干思考

大學數學教師怎樣準確認識學生的錯誤，游刃有余地矯治錯誤，達到對講授學科知識的深刻理解?本課題的研究給我們一些啟示：

第一，教師的學科知識具有促進學生在課題學習中獲得特殊智慧的特征。數學教師往往會在相關課題之間和課題內部的知識之間建立一些聯系，形成中心概念、概念序列或概念節點，而如何創設知識點之間的聯結并形成一定的“知識包”，則需要教師自覺總結或在教研活動中共同討論。

第二，多角度地考慮問題，討論各種解法，是數學發展的一種持續的動力，也是數學教學追求的目標。計算過程、推理路徑的多樣化，源于概念性理解。一個問題能用多種方法計算或論證需要超越知識表面的形式，把握數學的精髓——蘊含的數學概念和原理。

第三，教育教學活動是復雜的、多變的，僅僅具備學科基礎性知識，并不足以保證數學教師能夠勝任數學教育實踐工作[3]。雖然大部分教師能夠顧及學生的認知水平，但具體操作中，有良好的教學法知識的教師，能更有效地幫助學生認識錯誤、矯治錯誤，表現出了更有章法的指導策略。

總而言之，教師的學科知識不能自動地產生成功的教學方式和教學理念；缺乏堅固的學科支撐，成功的教學方式和新穎的教學理念不可能實現[4]。我們期望做一個“WJC+QLL+ZBD”型即學科專業扎實、教育教學智慧、實踐反思深刻、睿智耐心的數學教師，為了支持學生更深入學習高等數學，我們應該不斷積累、完善自己的數學教學知識結構，聚焦課堂教學實踐與反思，走向開拓性教學。

[1]黃興豐，馬云鵬.美國數學教師學科知識評價方法的述評[J].數學教育學報，2013，(1).

[2]馬 復.試論數學理解的兩種類型——從斯根普的工作談起[J].數學教育學報，2001，(3).

[4]馬立平.小學數學的掌握與教學[M].李士钅奇等譯.上海：華東師范大學出版社，2011.

[5]陳建華，劉金林，魏俊潮.線性代數(第3版)[M].北京：機械工業出版社，2011.

[6]陳建華，李立斌，凌 智，劉金林，陳惠香.基于問題解決的線性代數課程教學設計研究[J].高等理科教育，2011，(4).

(責任編輯：李文富)

Study on Mathematics Teachers' Teaching Strategies of Error Correction——Based on Error Handling in Students' Problem Solving

Chen Jian-hua1Wen Qing2

(1.Yangzhou University, Yangzhou, Jiangsu, 225002, China; 2.Chengdu University, Chengdu, Sichuan, 610106, China)

Teacher's discipline knowledge can't automatically produce successful teaching modes and teaching ideas.Without strong subject support,the success of teaching methods and new teaching ideas is impossible.In order to help students study more deeply,university mathematics teachers should accumulate and improve their mathematics teaching knowledge structure,focus on classroom teaching practice,and achieve the pioneering teaching.Through teachers' different teaching to students' incorrect answers, we can observe teachers' teaching ability of error correction.By means of the knowledge package involved with teaching content, this article discusses the depth and width of teachers' teaching content knowledge,their influence on teaching, and mathematics teachers' error correction strategies.

mathematics teachers;teaching strategies of error correction;matrices;zero factor;rank;systems of linear equations;knowledge

2014-03-09

揚州大學教改課題“基于數學理解的線性代數課程教學實踐研究”(YZUJX2012-46B)。

陳建華(1963—)，男，揚州大學副教授，碩士生導師。研究方向：線性代數。

G645

A

1674-6120(2014)06-0049-05