線性互補問題中幾類特殊矩陣與半正定矩陣之間的關系
孫艷波,蔣建林
(1.南京航空航天大學金城學院,江蘇南京211156;2.南京航空航天大學理學院,江蘇南京211156)
線性互補問題中幾類特殊矩陣與半正定矩陣之間的關系
孫艷波1,蔣建林2
(1.南京航空航天大學金城學院,江蘇南京211156;2.南京航空航天大學理學院,江蘇南京211156)
線性互補問題中特殊矩陣M的性質(zhì)是線性互補問題中研究的重要部分之一,本文深入研究了矩陣與半正定矩陣、子正定矩陣與半正定矩陣之間的關系,并且得到了特殊矩陣是半正定矩陣的一些充分條件.
半正定矩陣;Q0矩陣;C0矩陣;矩陣;子正定矩陣
1 引言
互補問題是一類新的數(shù)學模型,此模型的應用非常廣泛,比如經(jīng)濟學中的均衡問題、力學中的接觸問題、燃料油的加工提煉問題等[1-2].
互補問題作為線性規(guī)劃與二次規(guī)劃的推廣,如今已經(jīng)發(fā)展成為數(shù)學規(guī)劃理論中的一個獨立分支,所以它的解的存在性研究及算法的可行性研究受到了研究者的重視.
對于線性互補問題,矩陣M的特性與互補問題的解的存在性及算法的收斂性密切相關.所以要針對不同的矩陣類來研究線性互補問題.首先定義兩類矩陣:設M∈,如果對于任意的q∈,Lcp(M,q)都有解,則稱M為Q矩陣;如果對于給定的使得Lcp(M,q)可行的q,Lcp(M,q)有解,則稱M為Q0矩陣.(Q),(Q0)矩陣類的某些子矩陣類已經(jīng)得到了研究.廣義的半正定矩陣和正定矩陣(即不要求為對稱矩陣),分別為Q0矩陣和Q矩陣[3].但在一些實際問題構(gòu)造的Lcp(M,q)模型中,M往往都不是正定矩陣和半正定矩陣,為此,Fiedler,Ptak,Gale,Nikaido等推廣了正定矩陣和半正定矩陣的概念,提出了P矩陣,P0矩陣,S矩陣.文獻[3]證明了正定矩陣是P矩陣,且(P)?(Q),M∈(P)?Lcp(M,q)有唯一解.文獻[4]提出了C矩陣、C0矩陣、矩陣等概念,文獻[5]證明了當n=2時,若M∈()∩(Q0),則M是半正定矩陣.文獻[6]提出了子正定矩陣(記為PSBD矩陣),文獻[7]中給出了PSBD矩陣是半正定矩陣的一個充分條件.
本文在這些已有結(jié)論的基礎上,進一步研究了這些特殊矩陣之間的關系,對于∩Q0矩陣,在取消n=2的限制下,推導了其為半正定矩陣的充分條件.PSBD矩陣作為半正定矩陣的直接推廣,在二次規(guī)劃算法的研究中起著重要作用,本文從兩個方面給出了PSBD矩陣是半正定矩陣的充分條件.
定義2.1[4]如果對所有x≥0,xTMx≥0,則稱M為C0矩陣.
定義2.2[4]如果M∈(C0),且?x≥0,Mx≥0,xTMx=0可推出MTx≤0,則稱M為矩陣.設M∈,Mαα是M相應于下標集α的主子矩陣,若Mαα非奇異,那么矩陣A定義如下:
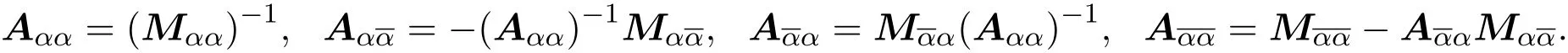
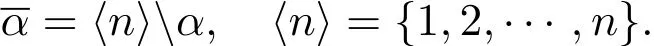
定義2.3[4]如果M的每個基主元變換都是C0矩陣,則稱M是矩陣.
引理2.1[5]設M∈∩(Q0),則M是半正定矩陣.
引理2.2[5]設M∈∩Rn×n,則下列條件等價:
(1)M∈(Q0);(2)對M的每個PPTA,aii=0?aij+aji=0,?i,j∈{1,2,···,n}.
定理2.1若M∈()∩∩(Q0)且rankM=1,則M是半正定矩陣.
證明當n = 1 , 2時,由引理2 . 1知M是半正定矩陣;當n≥3 ,設M∈且rankM=1,若M的對角元中至少有一個不為零(對角元全為零的情況不可能),設

則至少存在一個i使得ai和bi同時不為0,不妨設為i=1,這時m11=a1b1>0,取α={1},A=(M),即

注2.1定理中的條件rankM=1是必要的.例如,設
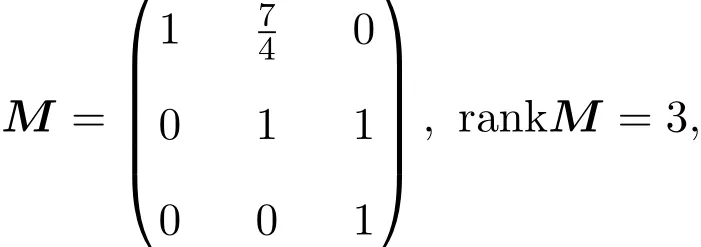
且對于基主元變換:

都是C0矩陣,從而
另一方面,由于det(M+MT)<0,所以M不是半正定矩陣.
3 PSBD矩陣與半正定矩陣
定義3.1[6]若?x∈,xTMx<0,可推出MTx≤0或MTx≥0,則稱M為PSBD矩陣.
引理3.1[7]若M∈是PSBD-矩陣且rankM≥2,那么MT∈(PSBD),且下列條件至少有一個成立:
(1)M是半正定矩陣;(2)(M+MT)≤0;(3)M∈().
引理3.2[7]設a?=b,a,b∈,且M=abT,那么M是PSBD矩陣當且僅當下列條件之一成立:
(1)存在t>0,使得b=ta;
(2)對所有t>0,b?=ta,且b≥0或b≤0.
引理3.3[7]設M=abT∈是PSBD矩陣,其中a,b∈,a,b?=0.假設?t>0,b?=ta,有a≥0或a≤0,那么M∈(Q0)當且僅當下列條件中至少有一個成立:
(1)M是半正定矩陣;
(2)a和b有相反的符號;
(3)a和b有相同的符號且當bi=0時,ai=0,?i∈{1,2,···,n}.
定理3.1設M∈∩(PSBD)∩(C0),rankM≥2,且M∈/則M是半正定矩陣.
證明因為M是PSBD矩陣,rankM≥2且M/∈(),由引理3.1知M是半正定矩陣或(M+MT)≤0中至少有一個成立.若(M+MT)≤0,則?x∈,有xT(M+MT)x≤0.
又由M∈(C0)知,
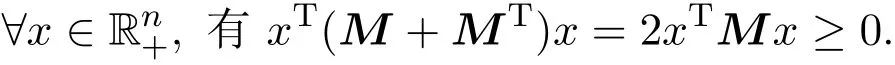

注3.1定理中的M/∈()以及rankM≥2是必要的.
例如,設
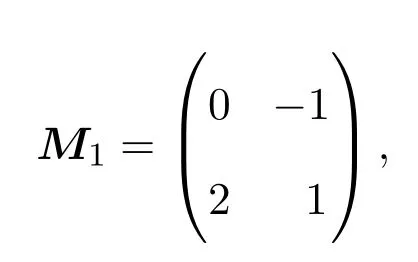
則M1∈()∩(PSBD)且rankM1=2,但M1不是半正定矩陣.另一方面,設

則
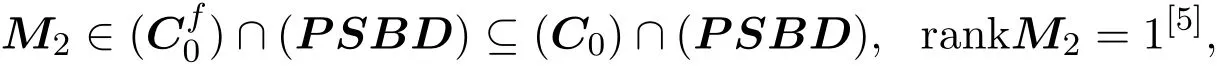
且M2/∈,但M2不是半正定矩陣.
特別地,當rankM=1時,我們有:
定理3.2設M=abT,其中a,b∈,M∈()∩(PSBD),且M∈(),則M是半正定矩陣.
證明假設M不是半正定矩陣.由M∈(PSBD)知M∈(MPSBD)(即M∈(PSBD),但M不是半正定矩陣),且M=abT,又M∈()?(C0),從而由引理3.2知a和b有相同的符號,由M∈()知,當bi=0時,ai=0,由引理3.3知M∈(Q0),從而有M∈()∩(Q0),且rankM=1,由定理2.1知M是半正定矩陣.
注3.2在注3.1中的第二個例子說明了在rankM=1的條件下,M∈()是必要的.下面的例子說明M∈()也是必要的.
設

M3∈()∩(PSBD),M3/∈,且rankM=1,但M不是半正定矩陣.
參考文獻
[1] Nagurney A,Dong J,Zhang D.A supply chain network equilibrium model[J].Transportation Research, 2002,38:281-303.
[2] 陳國慶,陳萬吉,馮恩民.三維接觸問題非線性互補原理及算法[J].中國科學:A輯,1995,25:1181-1190.
[3] Cottle R W,Pang J S,Stone R E.The Linear Complementarity Programming[M].Academic Press,New York,1992.
[4] Murthy G S R,Parthasarathy T.Some properties of fully semimonotone Q0-matrix[J].SIAM J.Matrix And Apl.,1995,16:1268-1286.
[5] Murthy G S R,Parthasarathy T.Fully copositive matrices[J].Math.Programming,1998,82:401-411.
[6] Crouzeix J P,Hassouni A.Positive subde fi nite matrices,generalized monoptonicity and linear compementarity problems[J].SIAM J.Matrix And Appl.,2000,22:66-85.
[7] Mohan S R,Neogy S K.Das A K.More on positive subde fi nnite matrices and the linear complementarity problem[J].Linear Algebra Appl.,2001,338:275-285.
The relationship between semi-de fi nite matrix and several types of special matrices in linear complementary problem
Sun Yanbo1,Jiang Jianlin2
(1.College of Jincheng,Nanhang Jincheng College,Nanjin211156,China; 2.College of Science,Nanhang Jincheng College,Nanjin211156,China)
The special matrix is an important part of the study of linear complementarity problem.In this paper,we study the relationship betweenmatrices and semi-de fi nite matrix,PSBD matrices and semide fi nite matrix.And we get some new conclusions about them.
semi-de fi nite matrix,Q0matrix,C0matrix,matrices,PSBD matrices
O211.1
A
1008-5513(2014)05-0480-05
10.3969/j.issn.1008-5513.2014.05.007
2014-07-10.
國家自然科學基金(11171013);江蘇省自然科學基金(BK2011719).
孫艷波(1979-),碩士,講師研究方向:線性與非線性規(guī)劃.
2010 MSC:30D30

