置換性很好的一類群
鐘艷林,曾吉文
(1.閩南理工學(xué)院信息管理系,福建泉州362700;2.廈門大學(xué)數(shù)學(xué)科學(xué)院,福建廈門361005)
置換性很好的一類群
鐘艷林1,曾吉文2
(1.閩南理工學(xué)院信息管理系,福建泉州362700;2.廈門大學(xué)數(shù)學(xué)科學(xué)院,福建廈門361005)
主要研究子群置換性質(zhì)對(duì)有限群結(jié)構(gòu)的影響.通過(guò)子群的置換性得到一類群,即B群.B群是全可置換群的擴(kuò)展,利用全可置換群的p次中心擴(kuò)張和子群的階得到B群的一些性質(zhì)并對(duì)B群的結(jié)構(gòu)進(jìn)行一些刻畫(huà).應(yīng)用B群的結(jié)構(gòu)得到有限p(p>2)群為二元生成的B群的充要條件.關(guān)鍵詞:有限群;B群;有限p群
1 基本知識(shí)
設(shè)G是有限群,記S1(G)={H|H是G的素?cái)?shù)冪階群},S2(G)={H|H是G的素?cái)?shù)階群,且|H|2||G|},若HΦ(G),K∈S1(G),總有HK=KH,則稱G是一個(gè)A群.若HΦ(G),K∈S1(G)?S2(G),總有HK=KH,則稱G是一個(gè)B群.如果G是A群,則G是全可置換群(見(jiàn)文獻(xiàn)[1]定理1.2).
從定義出發(fā),可以得到這樣的結(jié)論:若G是A群,則G是B群.若G是A群,則可以認(rèn)為不包含于Φ(G)的子群的置換性強(qiáng),G是全可置換群.這樣的群的結(jié)構(gòu)已知(見(jiàn)文獻(xiàn)[2]).若G是B群,則認(rèn)為不包含于(G)的子群的置換性稍弱一些.由定理2.1可以看出,G就是冪零群.提出問(wèn)題:若G是B群,則G是怎樣的?
2 主要結(jié)論及證明
定理2.1設(shè)G是B群.則
(1)G是冪零群.
(2)若P是G的一個(gè)Sylow子群,則G/P是B群.
(3)若P是G的一個(gè)Sylow子群,則P是B群.若1?=NP,則P/N是A群.
(4)若G是有限p群且不是A群,則G是外A群.
證明(1)任取P∈Sylp(G),其中,Sylp(G)表示G的Sylow子群,由p||G/Φ(G)|可知, P?∈Φ(G).任取P1∈Sylp(G),則PP1=P1P.由
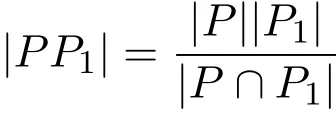
可知,|PP1|=|P|.因此P1?P.則G的Sylow p子群唯一.因此G是冪零群[3].
(2)設(shè)H/P≤G/P且H/P?≤Φ(G/P),K/P≤G/P且K/P∈S1(G/P)?S2(G/P).由G是冪零群,則可設(shè)
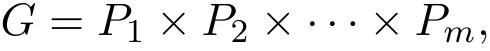
其中P是G的Sylow子群.因此K=K×P,其中K∩P=1.容易得到:
i11


因此HK=KH.則H/PK/P=K/PH/P.因此G/P是B群.
(3)由B群的定義易得P是B群.設(shè)H/N≤P/N且H/N?≤Φ(P/N),K/N≤P/N.不妨設(shè)

則|K|≥p2.從而K∈S1(P)?S2(P).由H?≤(P)可知,
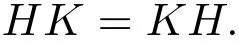
則H/NK/N=K/NH/N.因此P/N是A群.
(4)由G不是A群以及(3)可知結(jié)論.
由定理2.1(1)可知,一個(gè)B群為其Sylow子群的直積,故應(yīng)該對(duì)其Sylow子群進(jìn)行研究.由定理2.1(3)可知,一個(gè)B群的Sylow子群也是B群.因此對(duì)B群為有限p群進(jìn)行研究.
定理2.2設(shè)G是一個(gè)非交換的有限p群.若G是B群,則存在H≤G′∩Z(G),|H|=p,使得G/H是全可置換群.
證明取H≤G′且H是G的一個(gè)p階正規(guī)子群.顯然H≤Z(G)[4].由定理2.1(3)可知,G/H是A群.因此G/H是全可置換群.
定理2.3設(shè)G是一個(gè)有限p群,p>2,|G/Φ(G)|=pd,G=〈a1,a2,···,ad〉,T=〈a,b〉,其中a,b∈{a1,a2,···,ad}.
若G是B群,則T為下列群之一:
(1)Mp(1,1,1);(2)Cpm×Cpn;(3)非交換亞循環(huán)群.
證明若T交換,由d(T)=2可知:即定理中的(2).以下設(shè)T非交換.取H 情形1交換 則可以設(shè) 其中1≤i,j,k≤p. 此時(shí)討論參數(shù)n: 因此ab∈K〈a〉. 另一方面,ab=bac?∈〈b〉〈a〉?K〈a〉.這與ab∈K〈a〉矛盾. 情形2不交換 其中參數(shù)r,s,u,t是非負(fù)整數(shù)且滿足r≥1,u≤r.設(shè)T=〈a,b〉. 則可以設(shè) 其中1≤i,j,k≤p. 子情形1i?=p 由T′=〈[a,b],T3〉,通過(guò)計(jì)算容易得到,T′=〈aprxk〉,即T′循環(huán).因?yàn)椴唤粨Q,所以r+s+u>r.因此可以得到x∈T′. 若x?∈?1(T′),由T′循環(huán)可知T′=〈x〉.這與T′=〉矛盾.因此有 子情形2i=p 此時(shí) 若j?=p時(shí),則 顯然〈a〉〈b〉?T.因此T=〈a〉〈b〉.故T亞循環(huán).得到定理中(3)的一部分.因此總有j=p.此時(shí) 若k=p,則d(T)?=2.矛盾.所以總有k?=p.用xk替換x,有 通過(guò)計(jì)算容易得到apr+s+u?1∈Z(G). 令K=〈apr+s+u?1〉×〈b〉,則|K|≥p2.由〈a〉??(G),則〈a〉K=K〈a〉.因此ab∈K〈a〉. 另一方面, 這與〈a〉K=K〈a〉矛盾.因此沒(méi)有得到符合條件的群. 推論2.1設(shè)G是一個(gè)有限p群,p>2,|G/Φ(G)|=pd,G=〈a1,a2,···,ad〉,T=〈a,b〉,其中a,b∈{a1,a2,···,ad}. (1)若G是B群,則T也是B群. (2)設(shè)T1≤T,T2≤T,|T2|?=p.若G是B群,則T1T2=T2T1. 證明(1)由定理3可知,TMp(1,1,1)或者T為一個(gè)亞循環(huán)群.亞循環(huán)群都是A群,因此都是B群. 只需驗(yàn)證Mp(1,1,1)是B群.?K≤T且|K|?=p,則有KT.由B群定義可知, Mp(1,1,1)是B群.即T是B群. 推論2.2設(shè)G是一個(gè)有限p群,p>2.G是二元生成的B群當(dāng)且僅當(dāng)G為下列群之一: (1)Mp(1,1,1);(2)Cpm×Cpn;(3)非交換亞循環(huán)群. 證明(?)由定理3直接推出. (?)只需對(duì)定理中的群一一驗(yàn)證是B群.證明過(guò)程同推論4的證明. 推論2.3設(shè)G是一個(gè)有限p群,p>2,G是二元生成的B群.若H≤G,則H是一個(gè)B群. 證明只需對(duì)推論5中的群進(jìn)行驗(yàn)證.注意到亞循環(huán)群的子群都是亞循環(huán)群即可得到結(jié)論. [1]Kirtland J.Finite groups with all subgroups not contained in the Frattini subgroup permutable[J].Arch. Math.,2011,97:399-406. [2]Iwasawa K.Uber die endlichen Gruppen und die Verba nde ihrer Untergruppen[J].Fac.Sci.Imp.Tokyo Sect.,1941,14:171-199. [3]徐明曜.有限群導(dǎo)引(上冊(cè))[M].2版.北京:科學(xué)出版社,1999. [4]徐明曜,曲海鵬.有限p群[M].北京:北京大學(xué)出版社,2010. Some groups with a good permutability of subgroups Zhong Yanlin1,Zeng Jiwen2 The paper studies the in fl uence of subgroups replacement properties on the structure of fi nite groups. A fi nite group is derived from the subgroup replacement properties,which is called B group.B groups is the extension of full permutation groups,the power of p center expansion of full permutation groups and Subgroups order use to get some properties of B groups and descriptions about the structure of B groups.By using the structure of B group,we get the necessary and sufficient conditions of a fi nite p(p>2)group being a binary generating B group. fi nite groups,B groups, fi nite p groups O152 A 1008-5513(2014)05-0491-05 10.3969/j.issn.1008-5513.2014.05.009 2014-06-10. 福建省中青年教師教育科研項(xiàng)目(JB14108);福建省自然科學(xué)基金(2012J01022). 鐘艷林(1980-),碩士,講師,研究方向:有限群論及p群. 2010 MSC:20B05


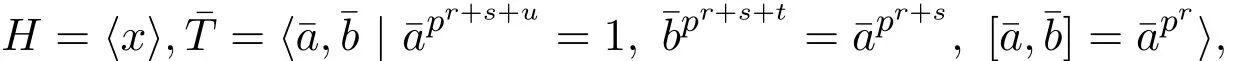
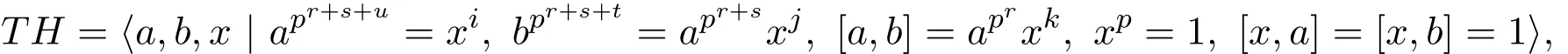
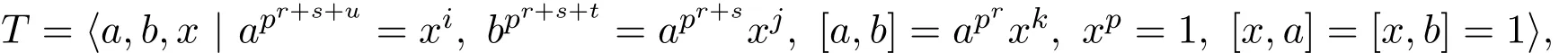


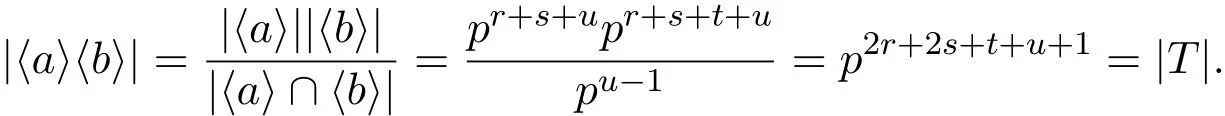

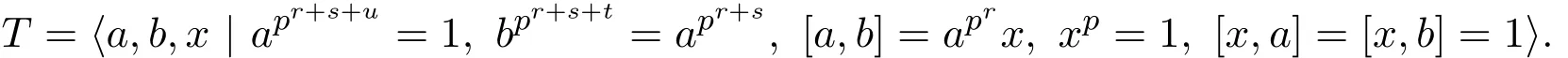

(1.Information Management Department,Minnan University of Science and Technology, Quanzhou362700,China; 2.School of Mathematical Science,Xiamen University,Xiamen361005,China)

