離散晶格的正族、負族及其Hamilton結構

常輝,屈哲,陶可勤

(青島濱海學院數學教研室,山東青島266555)

離散晶格的正族、負族及其Hamilton結構

常輝,屈哲,陶可勤

(青島濱海學院數學教研室,山東青島266555)

構造了一個新的等譜問題,利用相容性條件,推導出離散晶格方程的正族和負族.再利用跡恒等式,建立其Hamilton結構.獲得的離散方程族的達布變換、雙線性化、對稱、守恒率及其精確解也值得進一步研究.

晶格方程;正族;負族;跡恒等式;Hamilton結構

1 引言

許多物理、化學、生物現象都可以用離散晶格方程或連續的時間演化方程來描述,如: Toda晶格方程、離散或連續的KdV方程等.近年來,連續或離散可積方程族的研究引起研究人員極大的關注[1-5].尋找非線性可積方程族并研究其雙線性化、恒率、Hamilton結構及其精確解成為孤子理論的一個重要的課題[6-8].離散的時間演化方程族合適的等譜問題是這一課題的一個難點.本文設計了一個新的等譜問題,根據相容性條件,推導出其Lax可積的非線性離散的晶格方程的正族和負族.最后,利用跡恒等式建立了它們的Hamilton結構.

考慮如下離散的矩陣等譜問題:

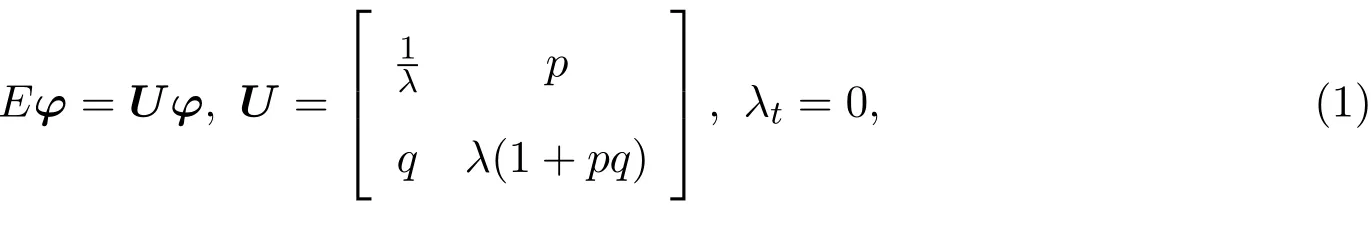
這里

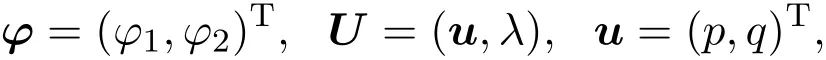
其中p=p(n,t),q=(n,t)是關于n和t的位勢函數,n∈Z,t∈R,λ是譜參數.令f=f(n)是一個離散的函數,如果E,E?1,D滿足下列關系:

Ef(n)=f(n+1),E?1f(n)=f(n?1),Df(n)=f(n+1)?f(n?1)=(E?1)f(n),n∈Z.則稱E是一個平移算子,E?1是它的逆算子,D是一個差分算子.

下面根據相應的時間譜矩陣Γ的不同情況,利用等譜問題(1)可以推出兩個不同的可積方程族,分別稱為正族與負族.

2 正的離散晶格方程族

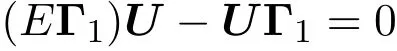
可以獲得下列方程:

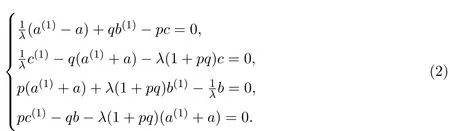
令

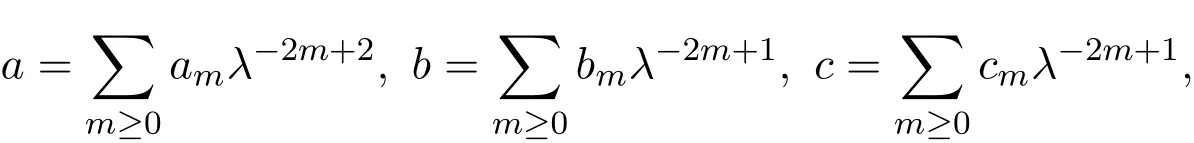
并把它們代入(2)式,可得

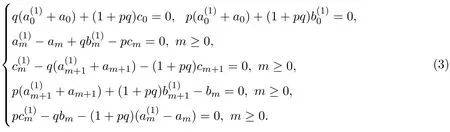
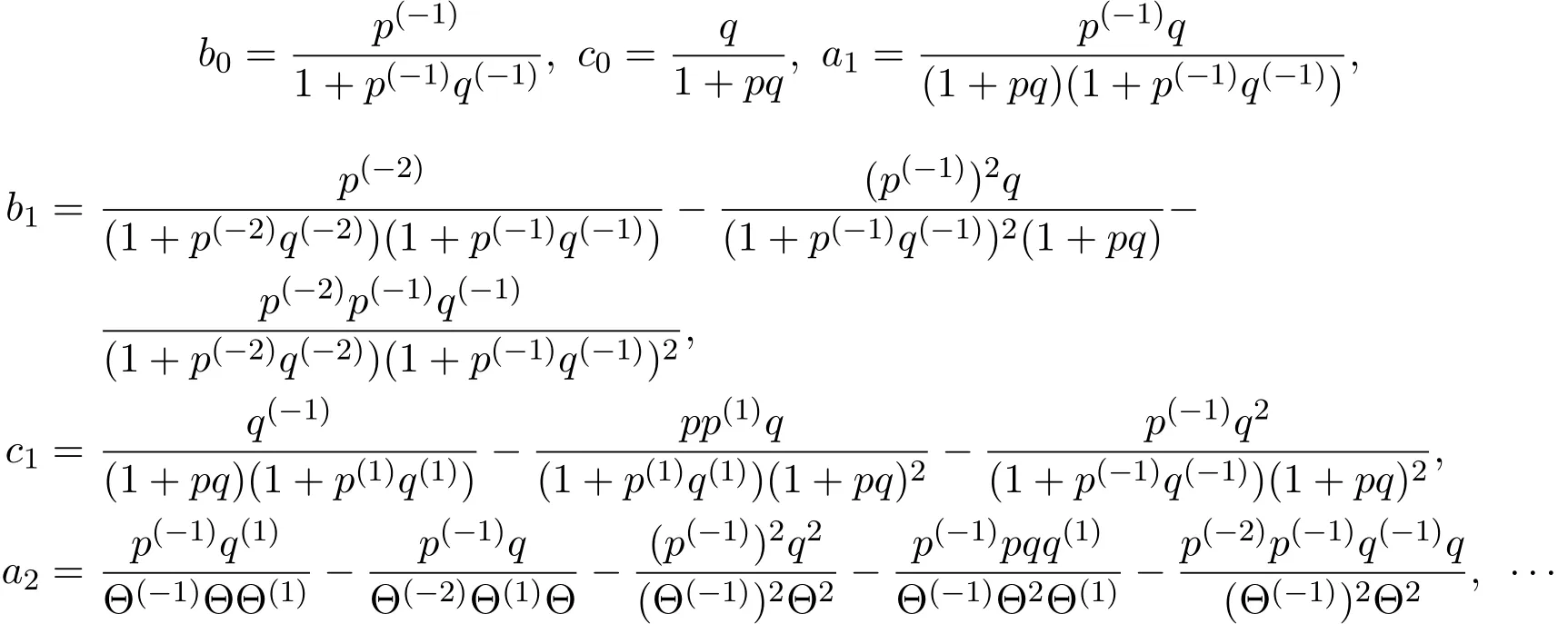
其中Θ=1+pq.根據文獻[1],容易證明am+1,bm,cm,m≥0都是局域的.

令

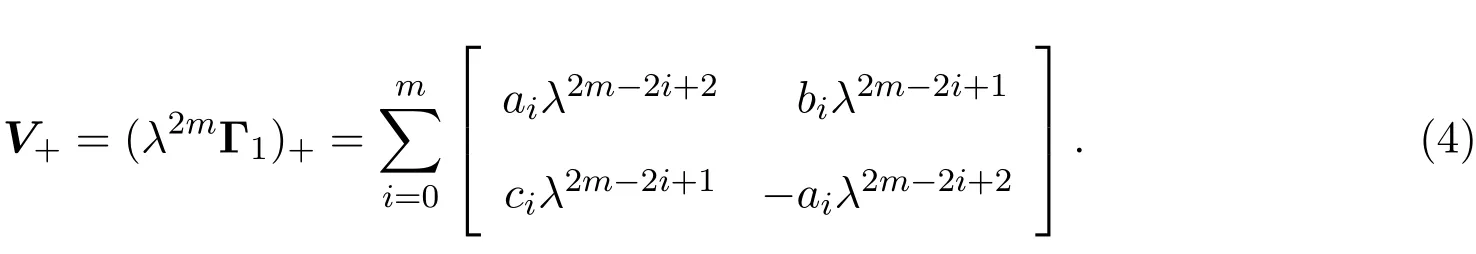
通過比較λ的次數,容易得到:

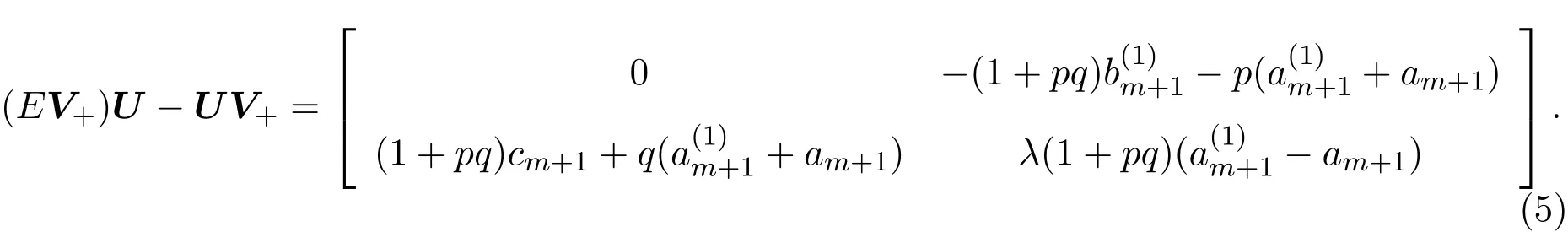
取Vm=V+,根據離散的零曲率方程Utm=(EV(m))U?UV(m),可以獲得Lax可積的離散方程族:

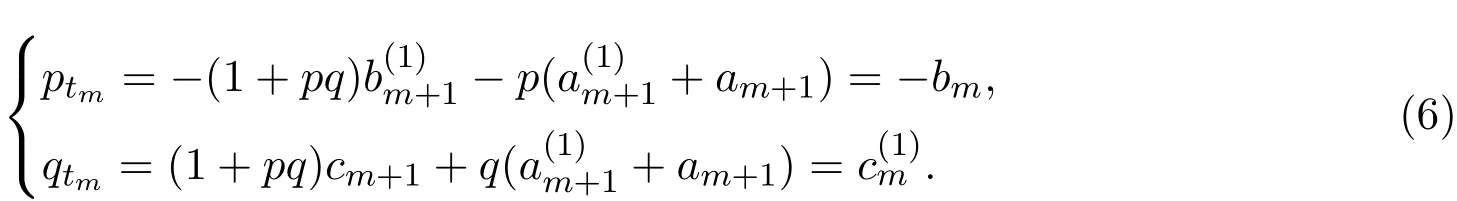
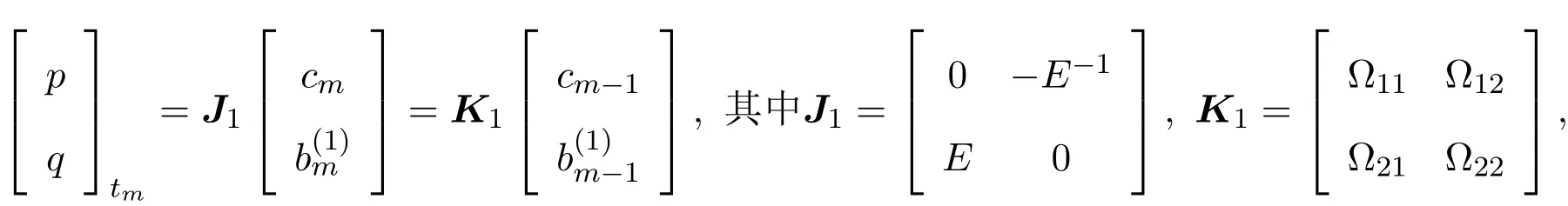
且

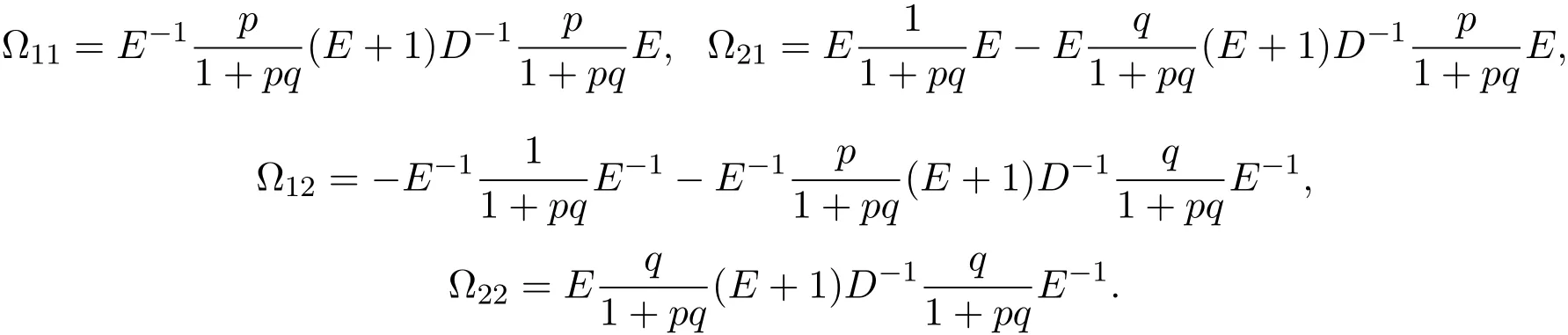
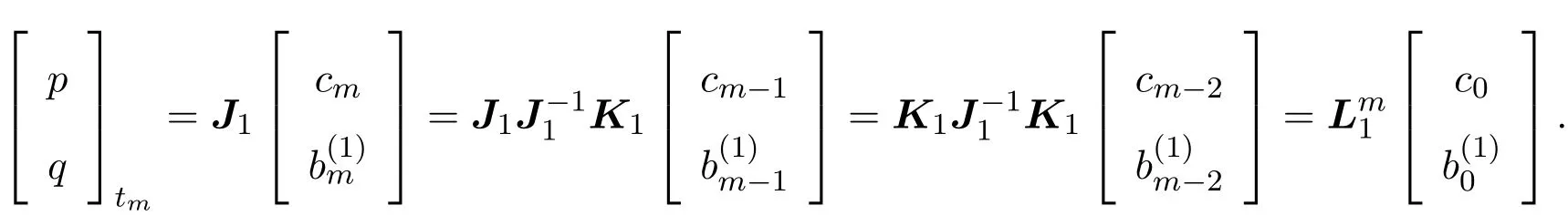
下面討論方程族(6)的Hamilton結構.

令

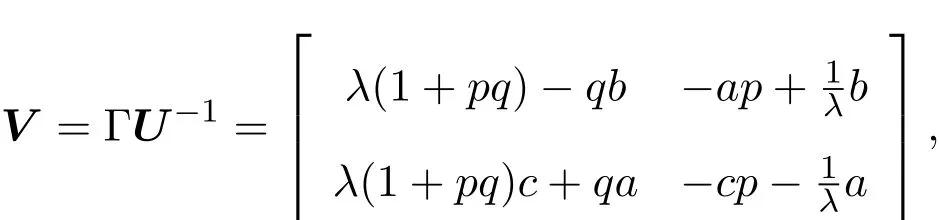
計算得

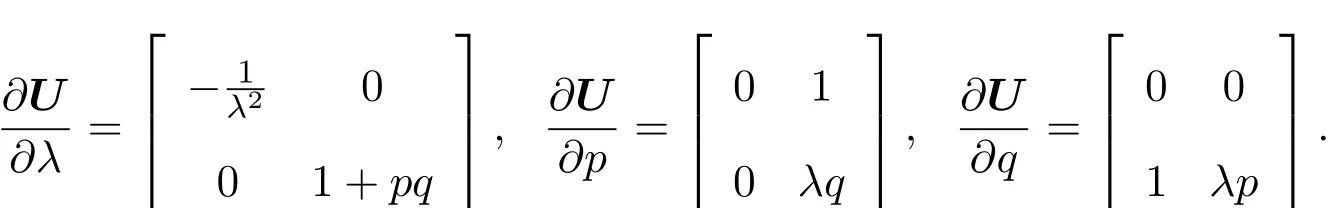
記〈A,B〉=tr(AB),這里A,B是方陣,“tr”表示方陣的跡.經計算可得:

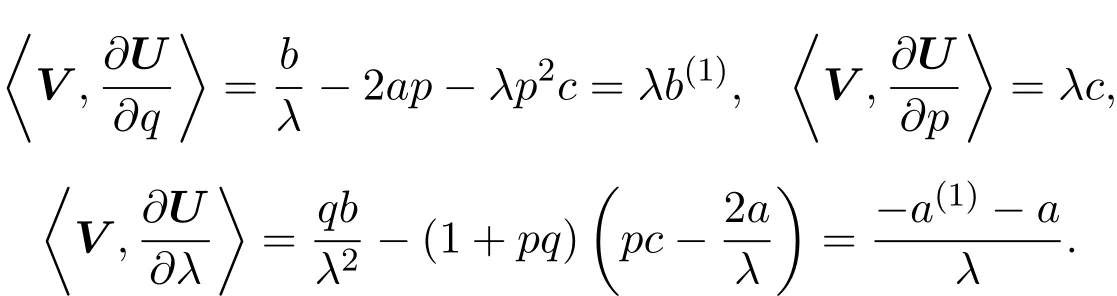
根據跡恒等式

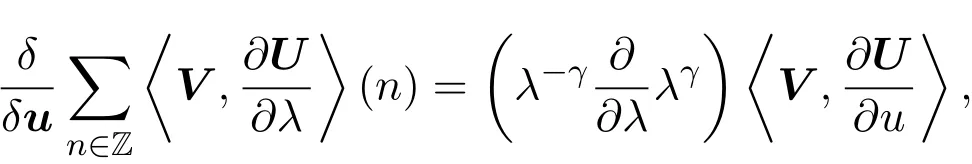
可得:

比較上式兩邊λ?2m+1的系數,得

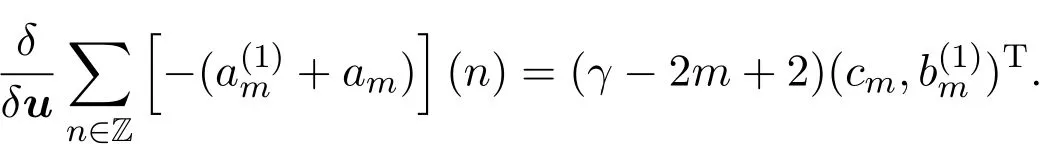
為了確定常數γ的值,上式兩端取m=0,可得γ=?2.從而(6)式可寫為:

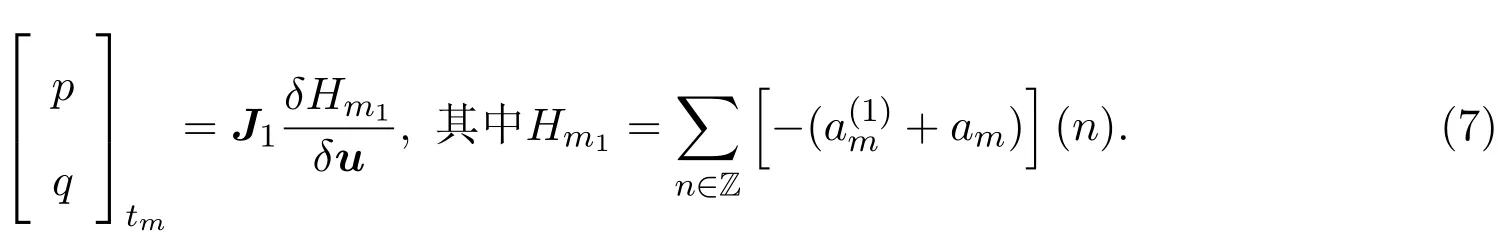
方程族(7)是在關系式(4)中λ次數為正號的情況下推導出來的.因此,稱此方程族為正的離散晶格族.

3 負的離散晶格方程族

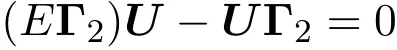
可以獲得下列方程:

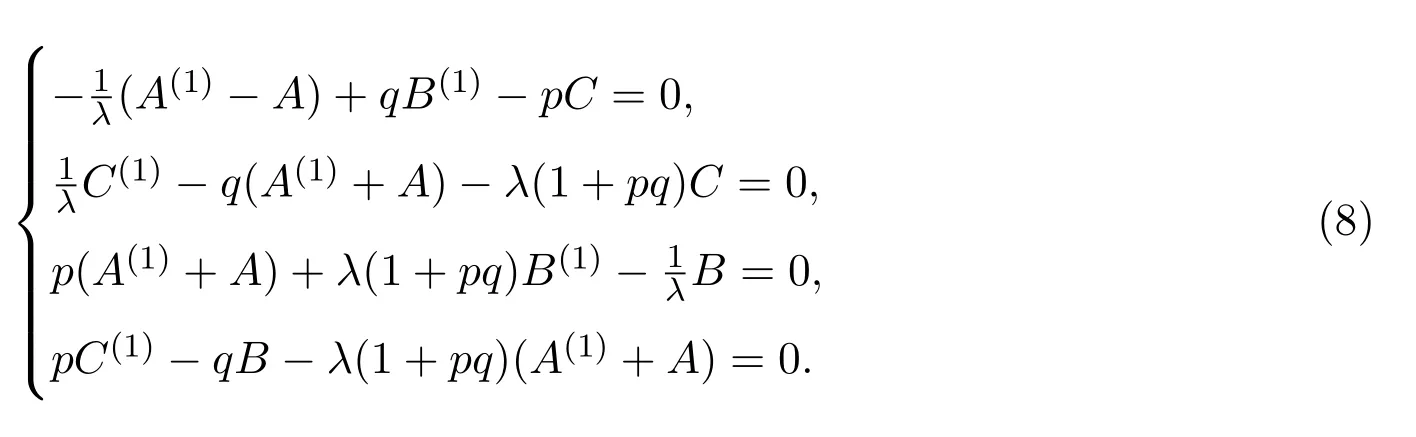
令

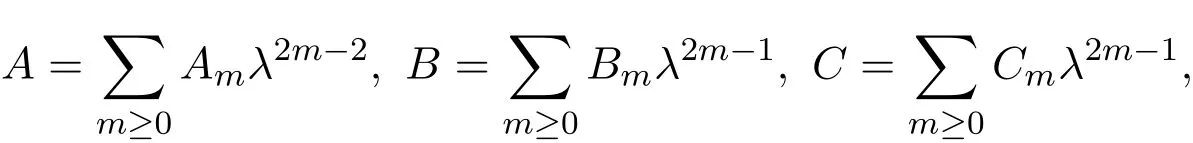
并把它們代入上述方程,可得

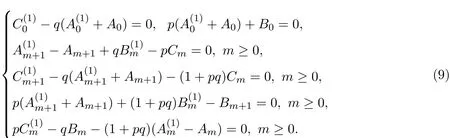
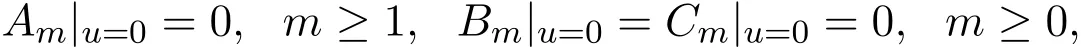
利用遞推關系(9),可以依次獲得:

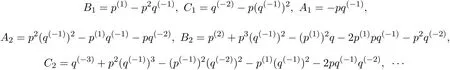
根據文獻[1],容易證明Am+1,Bm,Cm,m≥0都是局域的.

令

通過比較λ的次數,容易得到:

為了導出零曲率方程,選取修正項取?m=則

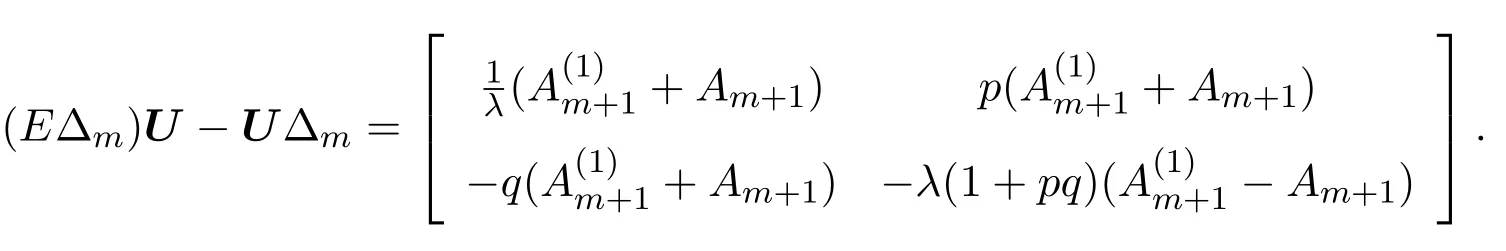
取Vm=V?+?m,則有

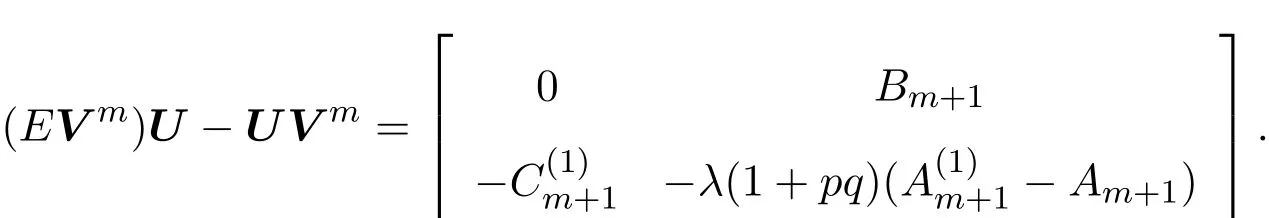
根據離散的零曲率方程Utm=(EV(m))U?UV(m),可以獲得Lax可積的離散方程族:

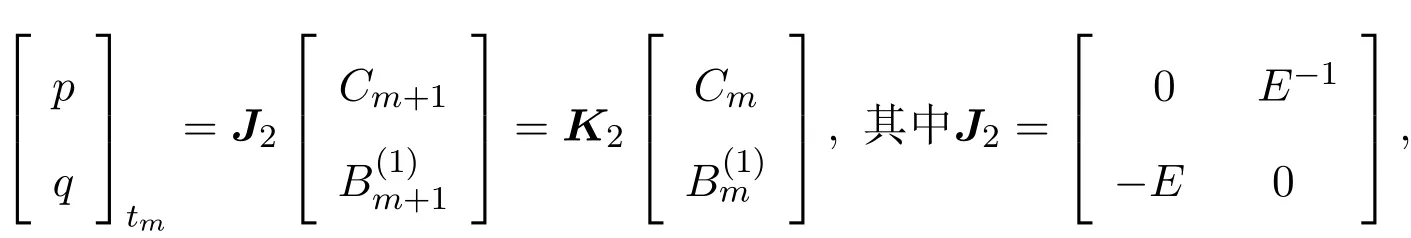
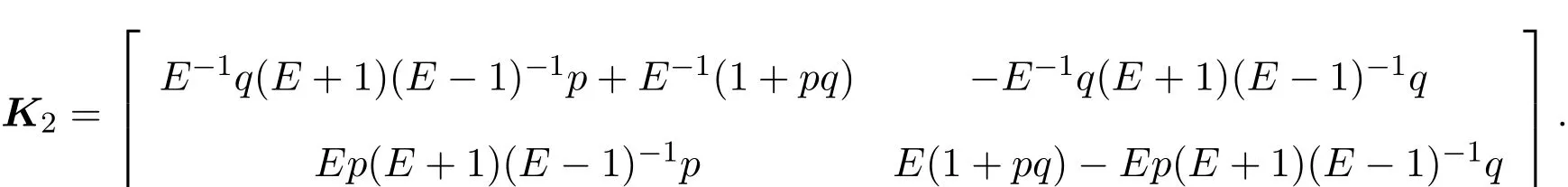
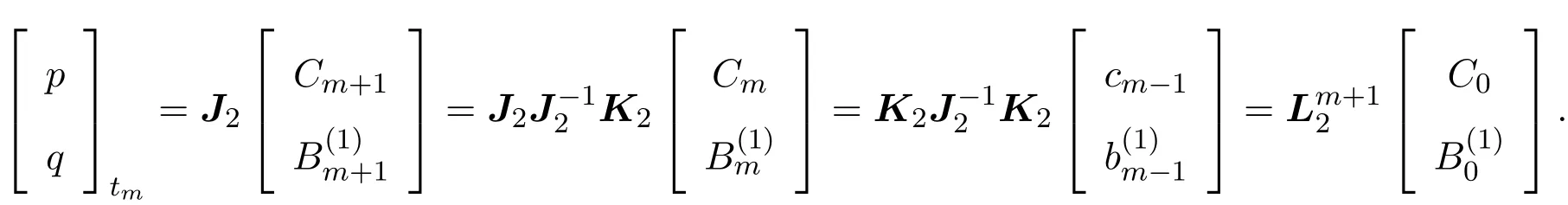
下面討論方程族(12)的Hamilton結構.

利用跡恒等式,通過運算可得:

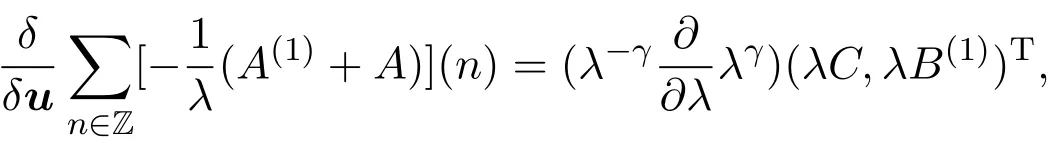
比較上式兩邊λ2m?1的系數,得

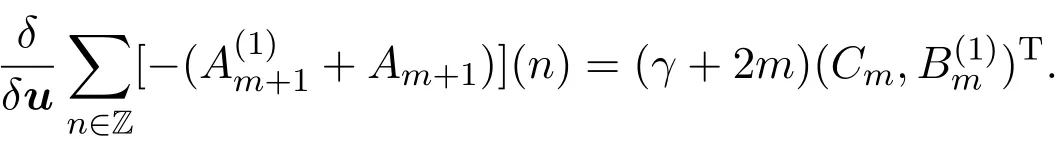
為了確定常數γ的值,上式兩端取m=0,可得γ=1.從而(12)式可寫為:

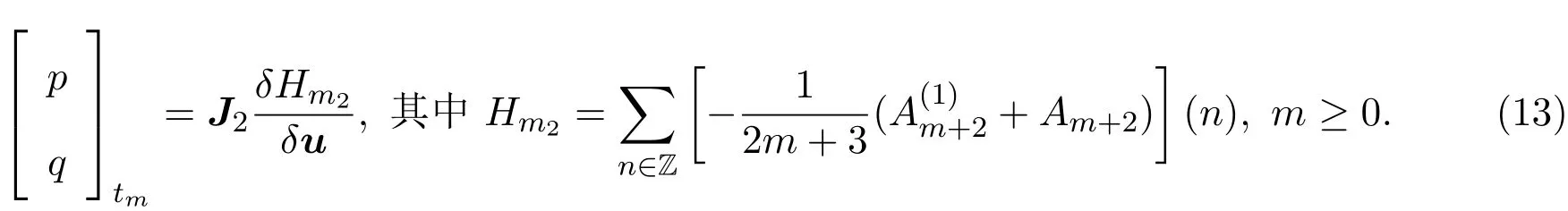
而方程族(13)是在關系式(10)的次數為負的情況下推導出來的,因此稱這個方程族為負族.

通過新構造譜問題(1),本文推導出兩個可積的方程族(6)和(12),并利用跡恒等式建立了它們的Hamilton結構(7)和(13).

參考文獻

[1] Tu Guizhang.A trace identity and its applications to the throry of discrete integrable systems[J].J.Phys. A:Math.Gen.,1990,23:3903-3922.

[2] 陳登遠.孤子引論[M].北京:科學出版社,2006.

[3] Zhang Yufeng,Yan Wang.A higher-dimensional Lie algebra and its decomposed Subalgebras[J].Physics Letters A,2006,360(1):92-98.

[4] Xu Xixiang.A hierarchy of discrete Hamiltonian equations and its binary nonlinear by symmetry constraint[J].Physics Letters A,2004,326:199-210.

[5] 常雙領.一個新的Lie代數和它的應用[J].純粹數學與應用數學,2013,29(6):627-633.

[6] Fu Jingli,Song Duan,Fu Hao,et al.Symmetries and conserved quantities of discrete wave equation associated with the Ablowitz-Ladik-Lattice system[J].Chinese Physics B,2014,22(9):1-6.

[7] 行姍,勾明,時振華.一類非線性時間演化方程的新的行波解[J],純粹數學與應用數學,2011,27(2):220-224.

[8] 聞小永.一個離散晶格方程的N波Darboux變換和無窮守恒率[J],數學的實踐與認識,2012,42(13):246-252.

A discrete positive hierarchy and a negative hierarchy as well as their Hamilton structures

Chang Hui,Qu Zhe,Tao Keqin
(Department of Mathematics,Qingdao Binhai University,Qingdao266555,China)

A new discrete spectral problem in the paper is devised,whose compatibility condition gives rise to a new positive hierarchy and a negative hierarchy of discrete integrable equations.Making use of the trace identity, their Hamiltonian structures are worked out respectively.The Darboux translation,bilinear form,symmetries, conservation laws,conserved quantities and their exact solutions of the resulting equation hierarchies are worth investigating in the future.

lattice equation,positive hierarchy,negative hierarchy,trace identity,Hamiltonian structure

O175

A

1008-5513(2014)05-0496-07

10.3969/j.issn.1008-5513.2014.05.010

2014-07-04.

山東省自然科學基金(ZR2011AQ017,ZR2010AM028).

常輝(1978-),碩士,講師,研究方向:可積系統與精確解.

2010 MSC:45G15