非齊次樹上馬氏信源的一類Shannon-McMillan定理
金少華,盧芳,陳秀引,王東
(河北工業大學理學院,天津300401)
非齊次樹上馬氏信源的一類Shannon-McMillan定理
金少華,盧芳,陳秀引,王東
(河北工業大學理學院,天津300401)
通過構造適當的非負鞅,將Doob鞅收斂定理應用于幾乎處處收斂的研究,給出了非齊次樹上m重非齊次馬氏信源的一類Shannon-McMillan定理.
非齊次樹;鞅;馬氏信源;Shannon-McMillan定理
1 引言
樹指標隨機過程已成為近年來發展起來的概率論的研究方向之一.強極限定理一直是國際概率論界研究的中心課題之一.文獻[1]利用隨機變量的截尾方法,給出了H可積下的相依隨機變量和的完全收斂定理以及強大數定理.文獻[2]利用ND隨機變量序列的矩不等式、極大值不等式以及隨機變量的截尾方法,研究了ND隨機變量序列部分和的大偏差結果和強收斂性.文獻[3]研究了兩兩NQD序列部分和完全收斂性的較一般形式,通過NQD序列的截尾方法以及相關引理,在較寬泛的條件下得到了一類較為廣泛的完全收斂性的結果.文獻[4]研究了一類隨機適應序列部分和的一類新的局部極限定理,得出了一些新結果,并進一步推廣了Borel-Cantelli引理.文獻[5]利用兩兩NQD列三級數定理的思想和Chebyshev不等式,研究了兩兩NQD列在一類廣泛條件下的弱大數定理和一類加強條件下的強大數定理,得到了與獨立情形一致的結果,還特別討論了同分布情形,推廣了相關文獻的結果.文獻[6]給出了樹指標馬氏鏈的定義并研究了其常返性及角常返性.文獻[7]研究了齊次樹上某些平穩隨機場的熵率.文獻[8]定義了在任意狀態空間取值的二叉樹上的分枝馬氏鏈,并研究了其極限定理.文獻[9]給出了Bethe樹上非齊次馬爾科夫隨機場的一類偏差定理.文獻[10]首先給出了在可列狀態空間取值的二叉樹上分枝馬氏鏈定義的離散形式,然后建立了二叉樹上分枝馬氏鏈的若干強極限定理,最后研究了二叉樹上有限狀態分枝馬氏鏈的強大數定理.文獻[11]研究給出了非齊次樹上二重馬爾可夫鏈的若干強極限定理.本文通過構造適當的非負鞅,將Doob鞅收斂定理應用于幾乎處處收斂的研究,給出了非齊次樹上m重非齊次馬氏信源的一類Shannon-McMillan定理.
2 定義
設T是一個具有根頂點O的無限樹,{Nn,n≥1}是一列正整數集,如果第n(n≥0)層上的每個頂點均與第n+1層上的Nn+1個頂點相鄰,則稱T為廣義Bethe樹或廣義Cayley樹.特別地,若對非負整數集N,用模m的同余關系對其分類得到模m的剩余類:
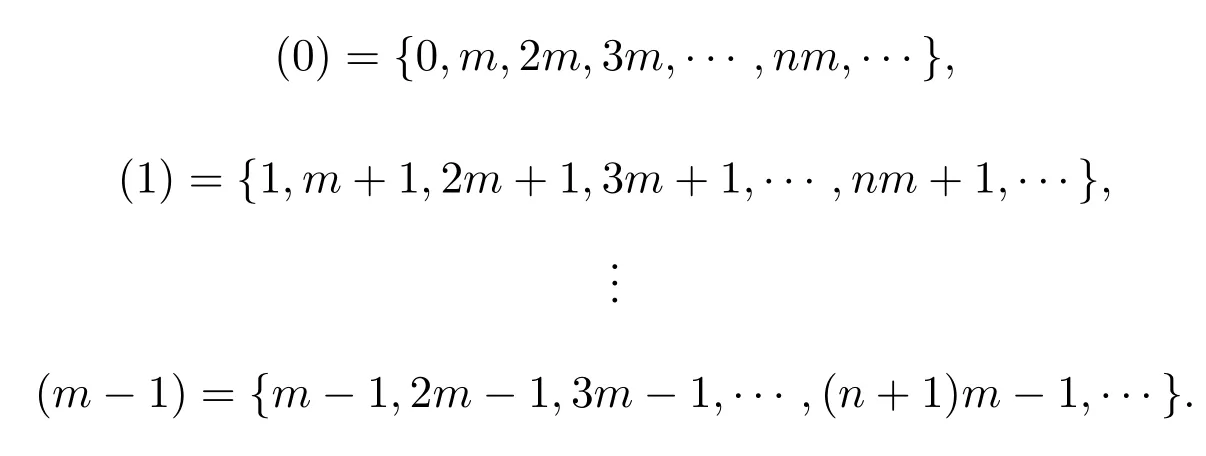
當n∈(i)時,令Nn+1=αi(αi均為正整數且不同時為1,i=0,1,2,···,m?1),就得到了一類特殊的非齊次樹Tα0,α1,··,αm?1.
以下恒以T表示樹Tα0,α1,··,αm?1,以Ln表示第n(n≥0)層上所有頂點的子圖,Tn表示含有從頂點O到第n層上所有頂點的子圖.S(t)表示頂點t的所有子代的子圖.
定義2.1[12]設(?,F,P)為一概率空間,Tn表示樹T上含有從o頂點到第n層上所有頂點的子圖,|Tn|表示子圖Tn的所有頂點數.{Xσ,σ∈T}是定義在該概率空間并于字母集S={s1,s2,···}上取值的任意信源,其聯合分布為:

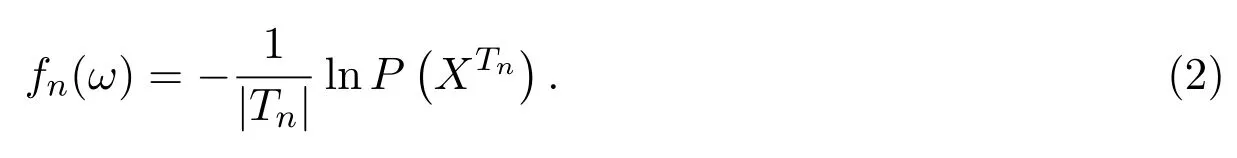
令則稱fn(ω)為{Xσ,σ∈T}的相對熵密度.
相對熵密度fn(ω)的極限性質在信息論中稱為Shannon-McMillan定理或信源的漸近均分割性,是信息論編碼的基礎.
定義2.2[13]如果存在STm?1上的分布
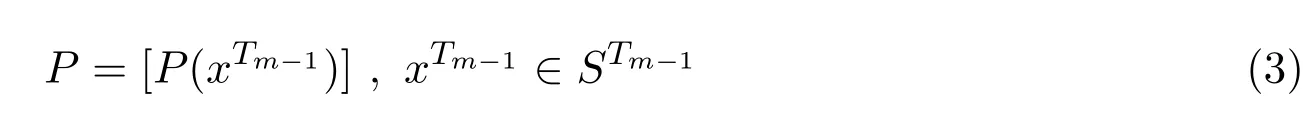
和一列定義在Sm+1上的條件概率組
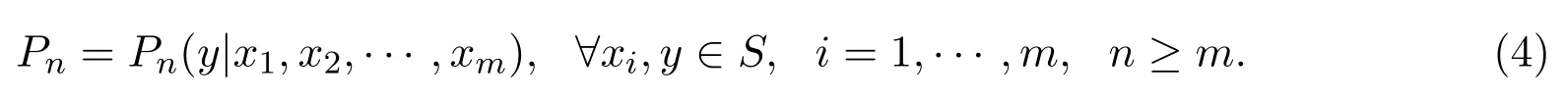
使得?σ,τ∈T,σ∈Ln,有
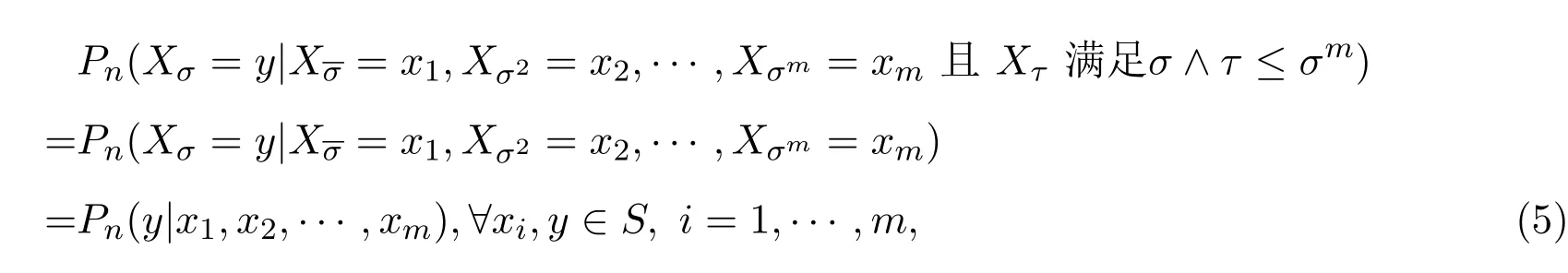
且

則稱{Xσ,σ∈T}為具有初始分布(3)與轉移矩陣列(4)的在S上取值的樹T上的m重非齊次馬爾可夫鏈.
在上述定義下,樹T上的非齊次馬爾可夫鏈的聯合分布為:
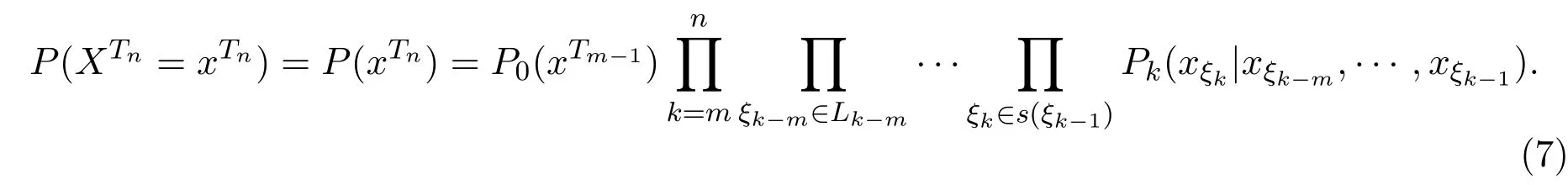
從而有
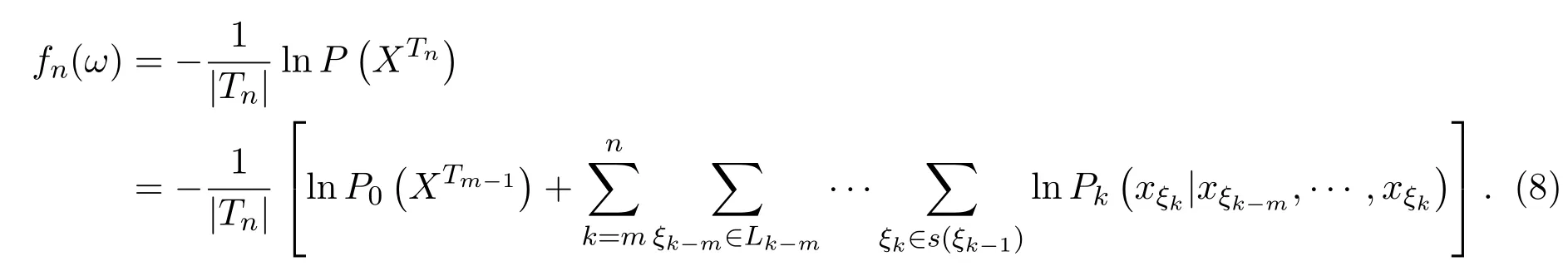
定義2.3[14]設
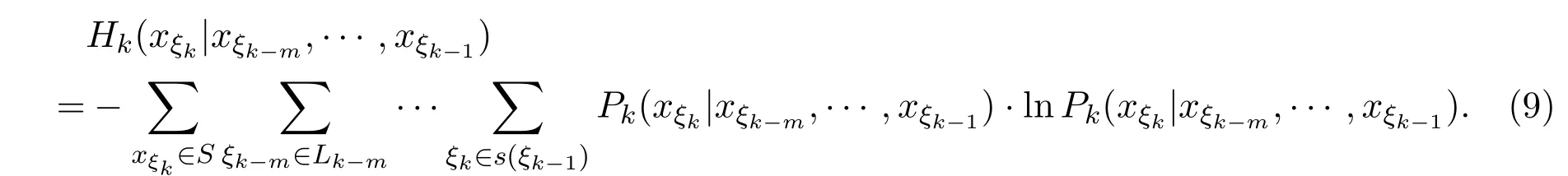
稱Hk(Xξk|Xξk?m,···,Xξk?1)為Xξk關于Xξk?m,···,Xξk?1的隨機條件熵.
3 主要結果及其證明
引理3.1設{Xσ,σ∈T}為具有初始分布(3)與轉移矩陣列(4)的取值于S的樹T上的m重非齊次馬爾可夫鏈,λ為一常數,令
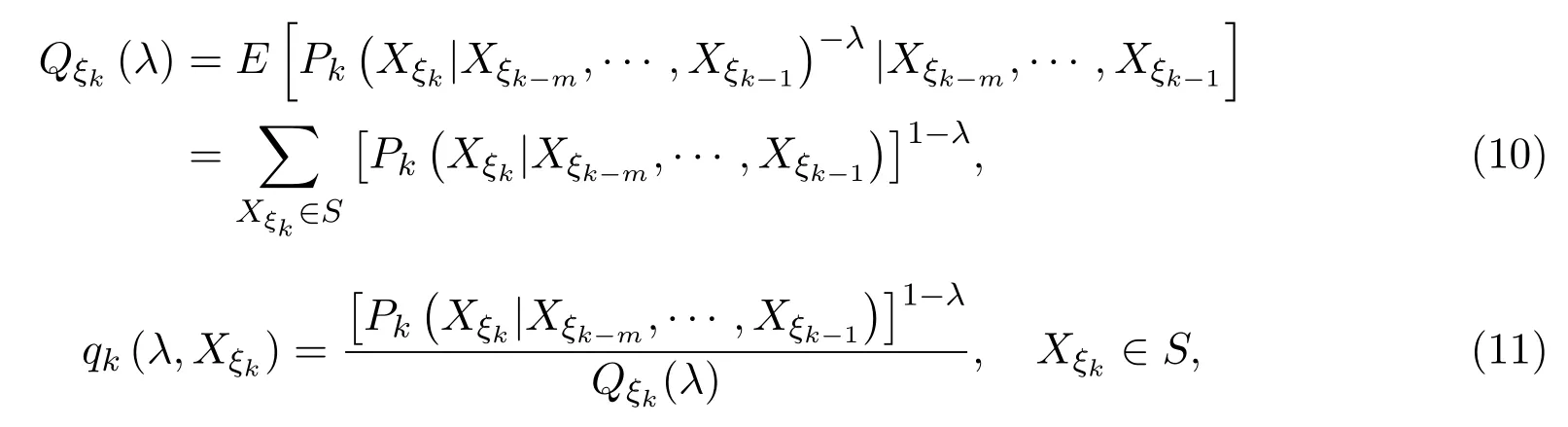
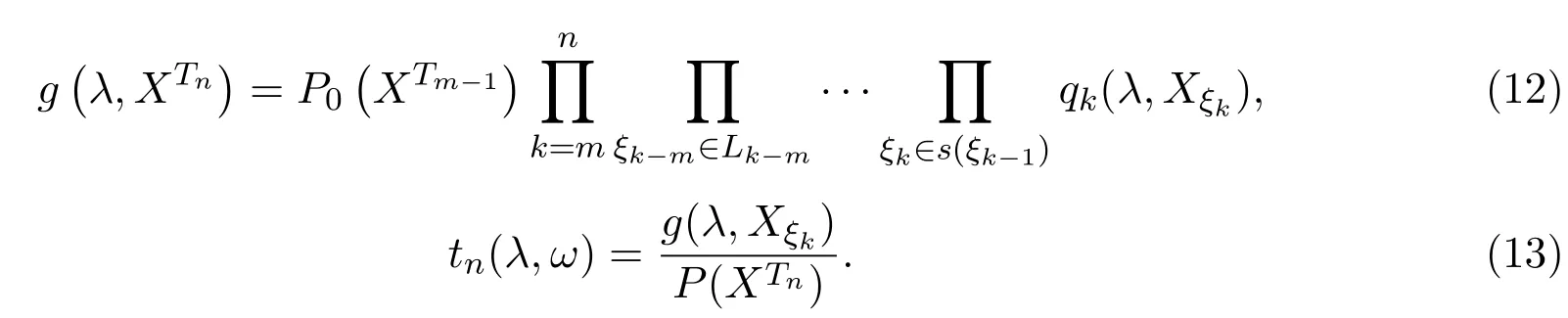
則{tn(λ,ω),σ(XTn),n≥m}是一非負鞅.
證明由于P(XLn=xLn|XTn?1=xTn?1)所以有
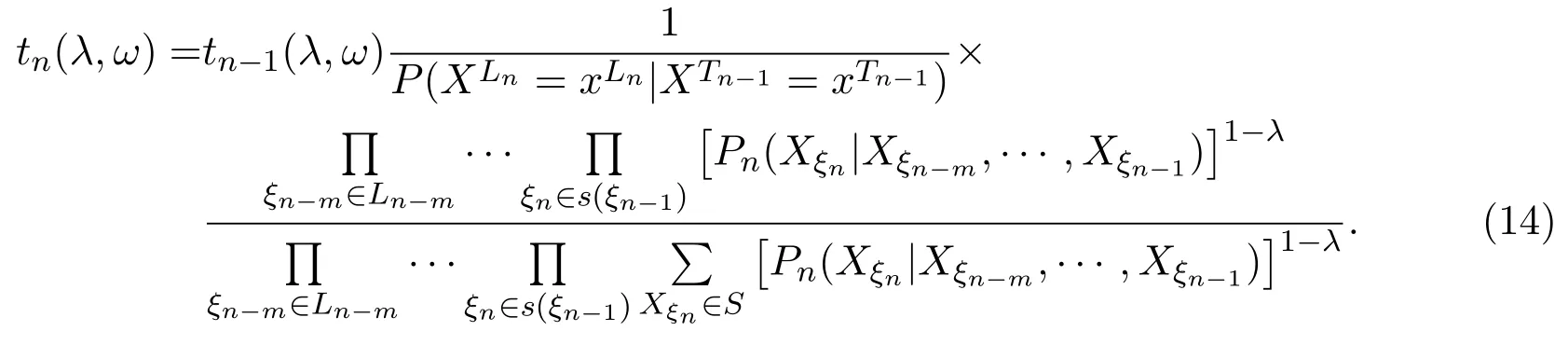
而

即
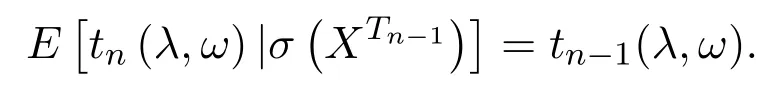
從而{tn(λ,ω),σ(XTn),n≥m}是一非負鞅.
定理3.1設{Xσ,σ∈T}為具有初始分布(3)與轉移矩陣列(4)且具有聯合分布(7)的非齊次樹T上的m重非齊次馬氏信源,fn(ω)與Hk(Xξk|Xξk?m,···,Xξk?1)分別由(8)式
和(9)式定義,設α>0,令
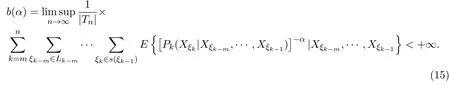
則有
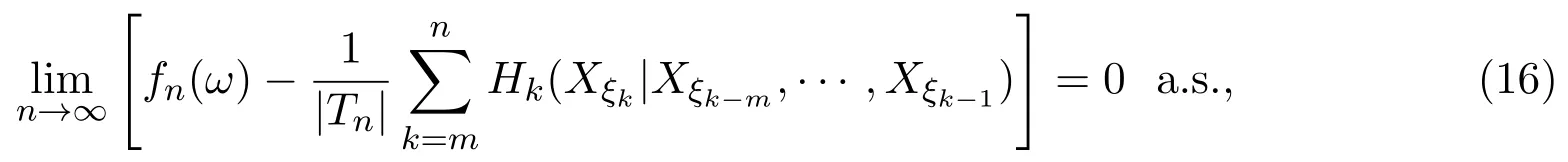
證明取(?,F,P)為所考慮的概率空間,由引理3.1知對任意的常數λ,
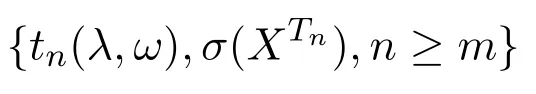
是一非負鞅.故由Doob鞅收斂定理知,存在A(λ)∈F,P(A(λ))=1,使得
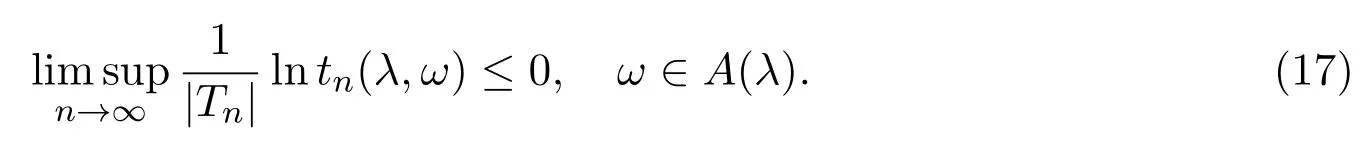
由(13)式與(17)式,有
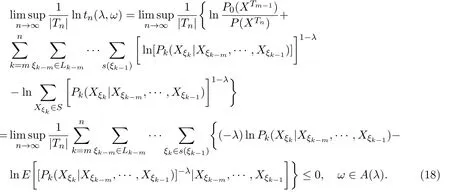
由(18)式,上極限的性質
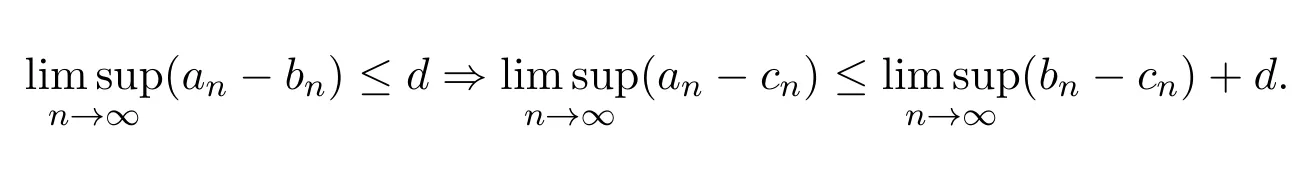
不等式
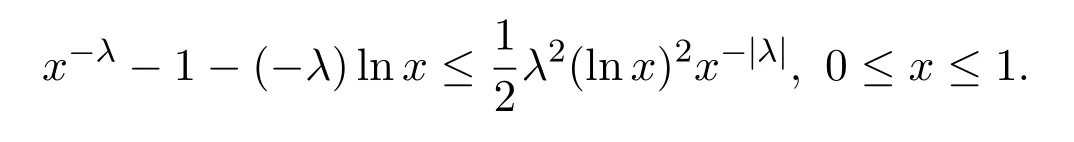
以及不等式
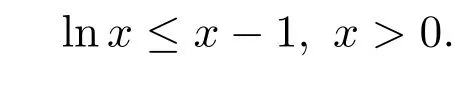
有
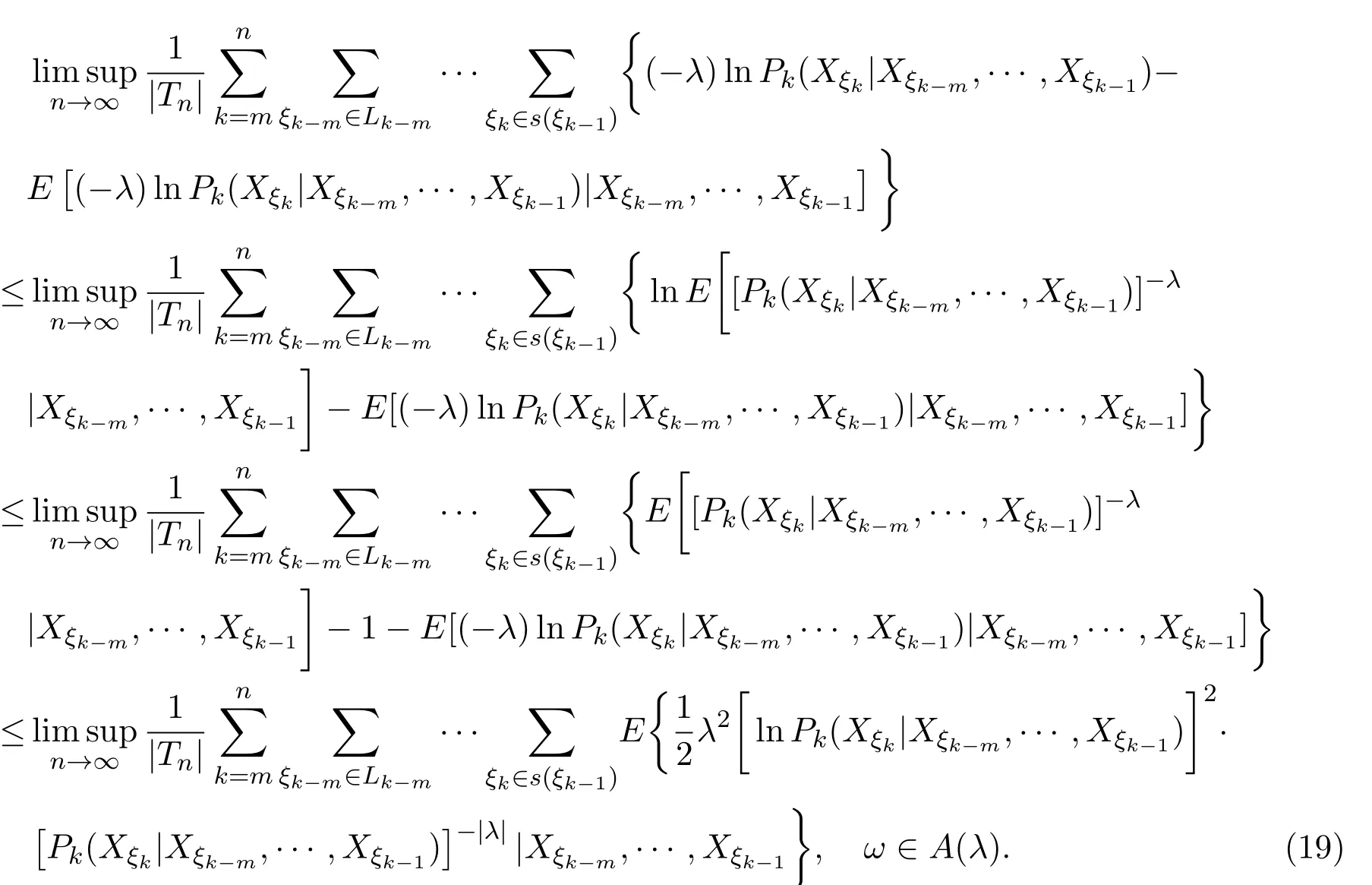
取0 因函數g(x)=(lnx)2xh,h>0,在處達到區間(0,1]上的最大值故有 當0<λ 取0<λi<α(i=1,2···),使得λi→0(i→∞).則對一切正整數i,由(22)式,有 類似地,當?α 與(23)式類似,可證得 由(23)式與(25)式,有 又由(9)式,有 于是由(26)式,有 推論3.1設{Xσ,σ∈T}為具有初始分布(3)與轉移矩陣列(4)且具有聯合分布(7)的非齊次樹T上的m重非齊次馬氏信源,fn(ω)與Hk(Xξk|Xξk?m,···,Xξk?1)分別由(8)式和(9)式定義,設α>0,令 則有 證明當0<|λ|<α時,由定理3.1證明中的(19)式,即 當0<λ<α時,將(29)式兩端同除以λ,得 取0<λi<α(i=1,2,···),使得λi→0(i→∞).則對一切正整數i,由(30)式,有 類似地,當?α<λ<0時,將(29)式兩端同除以λ,得 由(31)式和(32)式,有 由(33)式和(9)式,有(28)式成立. 參考文獻 [1] 施明華,周本達,趙建中等.H可積下的相依隨機變量和的完全收斂性質[J].純粹數學與應用數學, 2013,29(4):364-372. [2] 李旭,王學軍,劉小濤等.ND序列部分和的大偏差和強收斂性[J].純粹數學與應用數學,2011,27(6):808-813. [3] 施建華,林影.關于兩兩NQD序列部分和的完全收斂性[J].純粹數學與應用數學,2012,28(4):483-492. [4] 薛秀梅,楊衛國.一類隨機適應序列部分和的局部極限定理的一個注記[J].純粹數學與應用數學,2013,29(2):172-178. [5] 王志剛,歐宜貴.兩兩NQD列大數定律的一個注記[J].純粹數學與應用數學,2011,27(5):592-599. [6] Benjamini I,Peres Y.Markov chains indexed by trees[J].Ann.Probab.,1994,22:219-243. [7] Berger T,Ye Z.Entropic aspects of random fi elds on trees[J].IEEE Trans.Inform.Theory,1990,36:1006-1018. [8] Guyon J.Limit theorems for bifurcating Markov chains.Application to the detection of cellular aging[J]. Ann.Appl.Probab.,2007,17:1538-1569. [9] Yang W G.A class of deviation theorems for the random fi elds associated with nonhomogeneous Markov chains indexed by a Bethe tree[J].Stochastic Analysis and Applications,2012,30(2):220-237. [10] 黨慧,楊衛國,高榮,等.二叉樹上分枝馬氏鏈的強大數定理[J].純粹數學與應用數學,2013,29(5):529-535. [11] 金少華,霍艷,崔春紅,等.一類特殊非齊次樹上二重馬爾可夫鏈的若干強極限定理[J].數學的實踐與認識, 2013,43(2):218-223. [12] 金少華,呂潔.一類非齊次樹上非齊次馬氏信源的Shannon-McMillan定理[J].河北工業大學學報, 2012,41(2):19-22. [13] 金少華,宛艷萍,陳秀引,等.非齊次樹上m階非齊次馬氏鏈的一類強偏差定理[J].河北工業大學學報, 2013,42(2):61-66. [14] 王康康.任意信源關于賭博系統的一類Shannon-McMillan定理[J].純粹數學與應用數學,2008,24(2):353-357. A class of Shannon-McMillan theorems for Markov information source on a non-homogeneous tree Jin Shaohua,Lu Fang,Chen Xiuyin,Wang Dong In this paper,by constructing non-negative martingales and appliying Doob′s martingale convergence theorem to the research of a.e.convergence,a class of Shannon-McMillan theorems for m-order non-homogeneous Markov information source on a non-homogeneous tree are given. non-homogeneous tree,martingale,Markov information source,Shannon-McMillan theorem O177.91 A 1008-5513(2014)04-0331-10 10.3969/j.issn.1008-5513.2014.04.001 2014-01-30. 河北省高等學校科學技術研究重點項目(ZD2014051). 金少華(1965-),博士,教授,研究方向:概率極限理論. 2010 MSC:60B12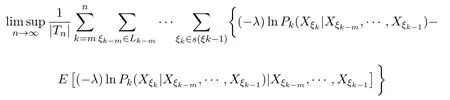
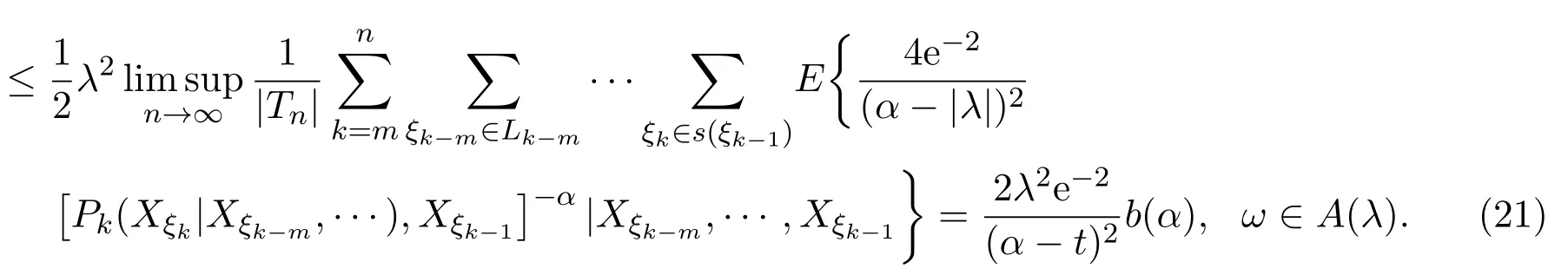
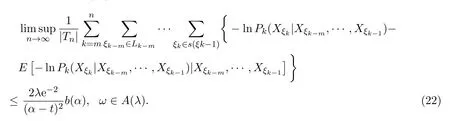
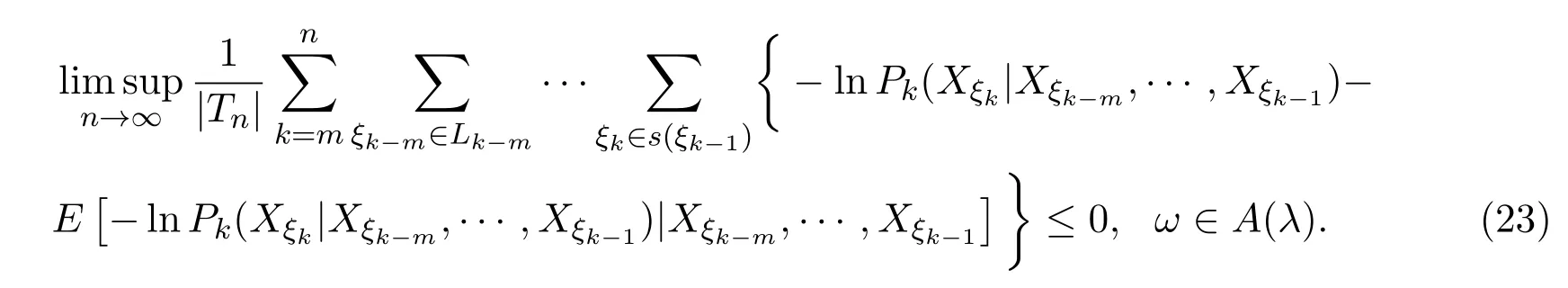
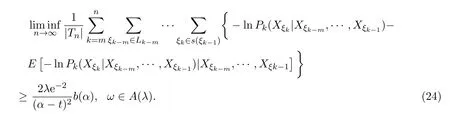

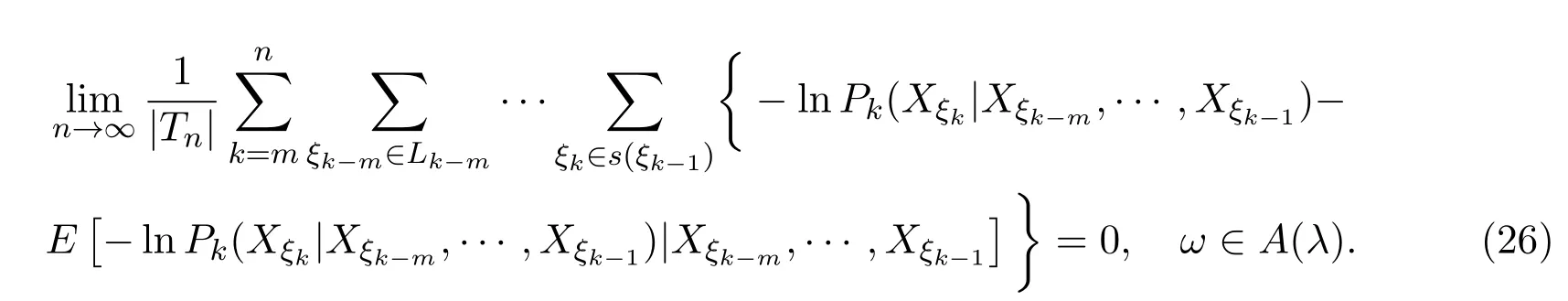
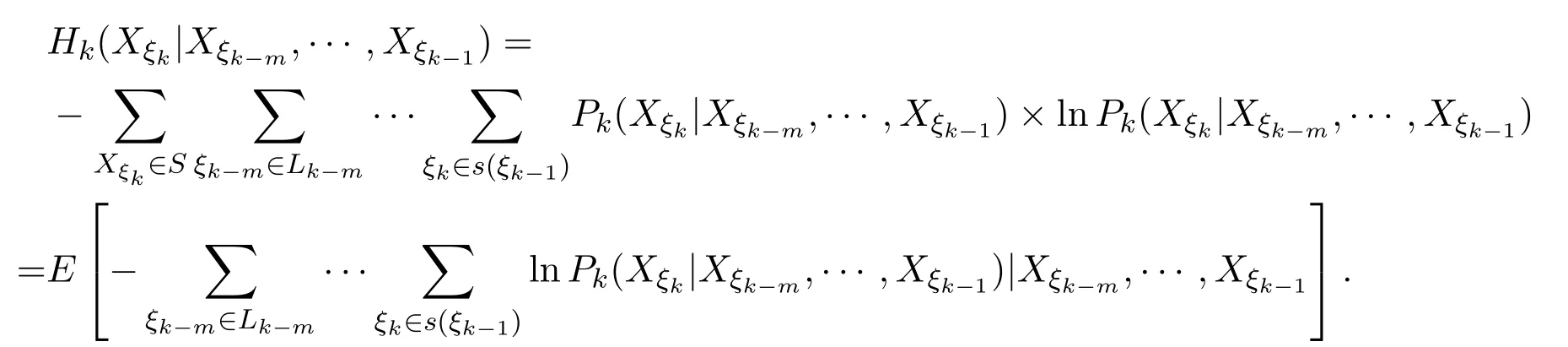
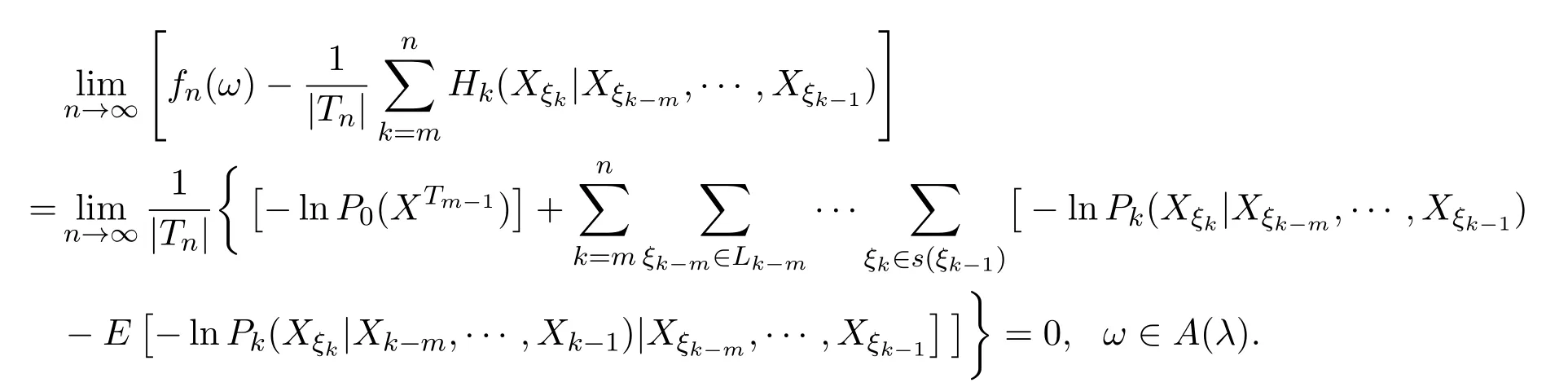
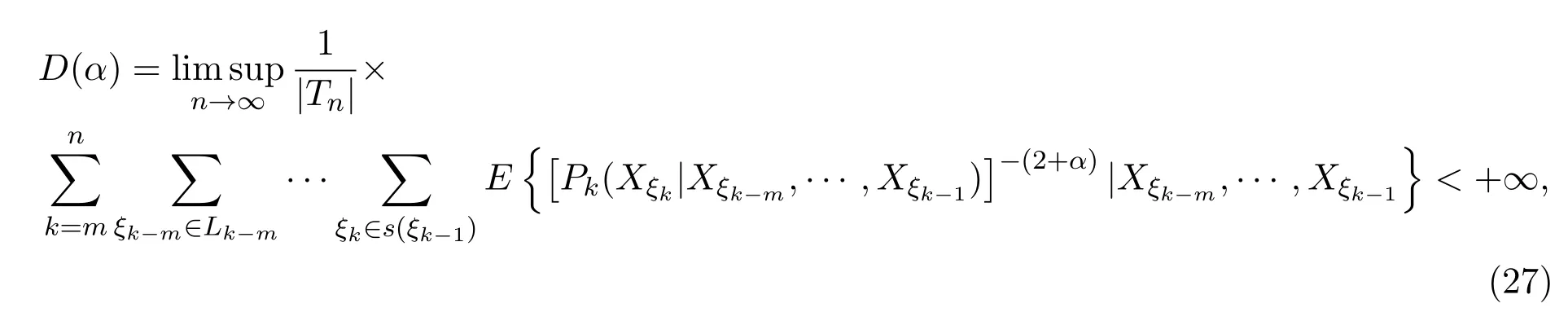
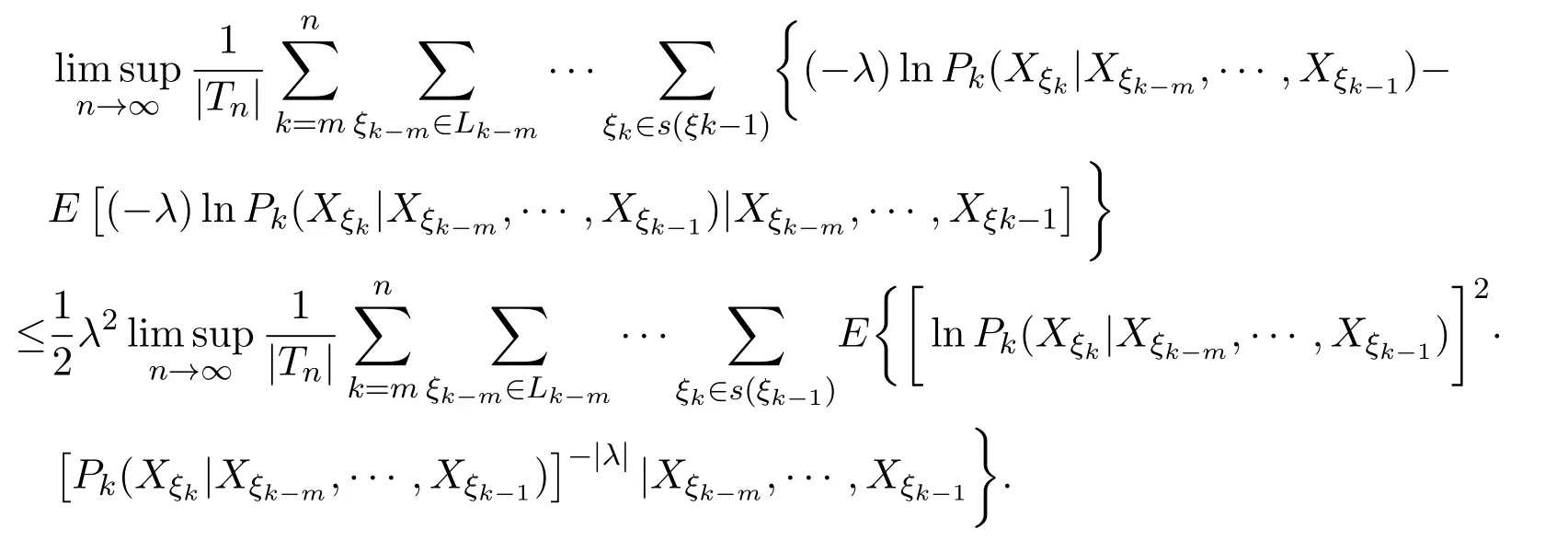
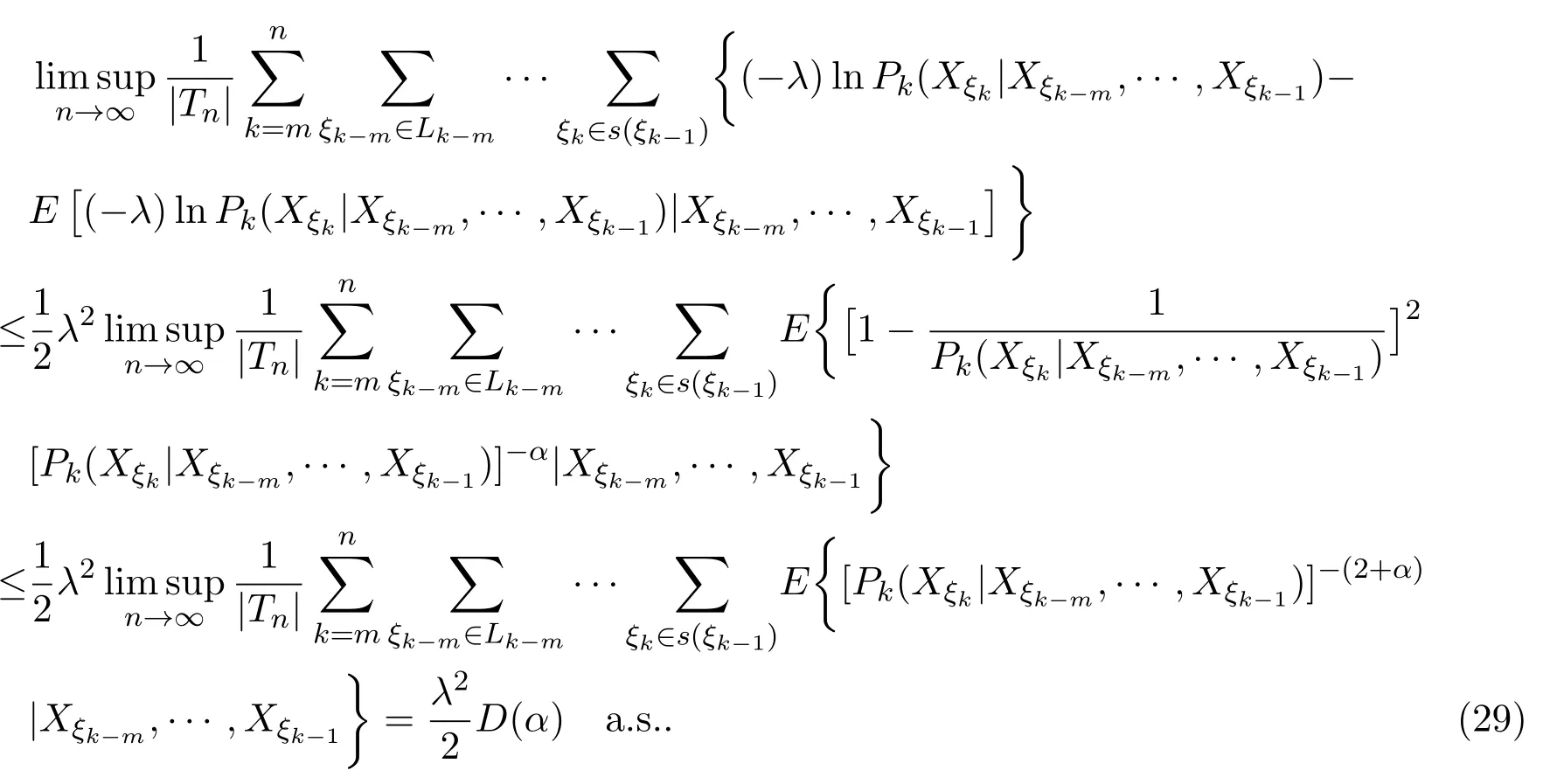
(College of Science,Hebei University of Technology,Tianjin300401,China)

