關(guān)于一類半環(huán)上的格林關(guān)系的若干研究
練利鋒, 任苗苗, 陳益智
(1.西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127;2.廣東惠州學(xué)院數(shù)學(xué)系,廣東 惠州 516007)
關(guān)于一類半環(huán)上的格林關(guān)系的若干研究
練利鋒1, 任苗苗1, 陳益智2
(1.西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127;2.廣東惠州學(xué)院數(shù)學(xué)系,廣東 惠州 516007)
研究了加法半群是帶,乘法半群是完全正則半群的半環(huán)上的格林關(guān)系,給出了是同余關(guān)系的充分必要條件,證明了由這些同余關(guān)系所決定的半環(huán)類都是半環(huán)簇,并給出了這些半環(huán)簇的積分解.
半環(huán);簇;同余;格林關(guān)系
1 引言及預(yù)備知識(shí)
設(shè)(S,·)是半群,若S的每個(gè)元素都是完全正則元(即對(duì)任意的a∈S,若存在x∈S使得a=axa且ax=xa)則稱S是完全正則半群.文獻(xiàn)[1]深入研究了完全正則半群,并從冪等元的角度對(duì)完全正則半群進(jìn)行了分類.完全正則半群的每個(gè)H-類都是群(見文獻(xiàn)[2-3]), Ha表示a所在的H-類,a0表示群Ha的單位元.
設(shè)(S,+,·)是(2,2)-型代數(shù),其中“+”和“·”是二元運(yùn)算.若S滿足下列條件: (1)(S,+)和(S,·)是半群;
(2)(S,+,·)滿足等式x(y+z)≈xy+xz和(x+y)z≈xz+yz;
則稱(S,+,·)是半環(huán).格林關(guān)系在半群理論發(fā)展過程中扮演著非常重要的角色,因此對(duì)格林關(guān)系的研究是有意義的.從代數(shù)角度來說,半環(huán)可以看做是由分配律聯(lián)系著的同一非空集合上的兩個(gè)半群,而半環(huán)的乘法半群和加法半群都有各自的格林關(guān)系,因此對(duì)半環(huán)的乘法半群和加法半群的格林關(guān)系的研究也是很有必要的.文獻(xiàn)[4-8]對(duì)冪等元半環(huán)進(jìn)行了深入細(xì)致的研究,并借助冪等元半環(huán)的格林關(guān)系研究了冪等元半環(huán)簇的L-子簇和D-子簇(見文獻(xiàn)[5-6]),得到了許多重要結(jié)論.
設(shè)S是半環(huán),若S滿足附加恒等式:則對(duì)任意的 a∈S,由aan?2a=a且 aan?2=an?1=an?1a,可知 (S,·)是完全正則半群.因此將滿足 (1),(2),(3)這三個(gè)附加恒等式的所有半環(huán)作成的簇記為 ˉCR,并將(S,+)上的格林L(R,D)關(guān)系記為(S,·)上的格林L(R,D)關(guān)系記為本文主要研究中半環(huán)上的格林關(guān)系,并給出下列各種關(guān)系的刻畫,證明了由這些關(guān)系所決定的半環(huán)簇都是的子簇,最后通過積得到了這些子簇之間的關(guān)系:


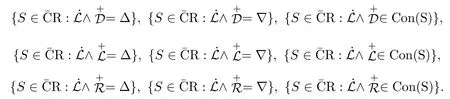
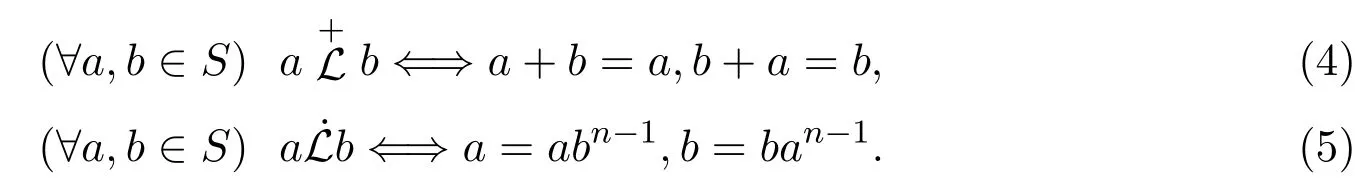
由文獻(xiàn)[1]可知,任一完全正則半群S都是完全單半群的半格S=(Y,Sα),其中Y與S/J同構(gòu),Sα是S的J?類.且有
引理 1.1[1]設(shè)S=(Y,Sα)是完全正則半群,a∈Sα,b∈Sβ,其中α≤β,則有:
(i)a0=(aba)0;(ii)a L ba,a R ab;(iii)a=a(ba)0=(ab)0a.
引理 1.2[1]設(shè)(S,·)是完全正則半群,則D=J是S上的同余關(guān)系.
引理 2.1設(shè)則是S上的同余關(guān)系.
證明顯然是(S,+)上的同余關(guān)系.下證是 (S,·)上的同余關(guān)系.已知是等價(jià)關(guān)系,故只需證明關(guān)于乘法滿足相容性即可.
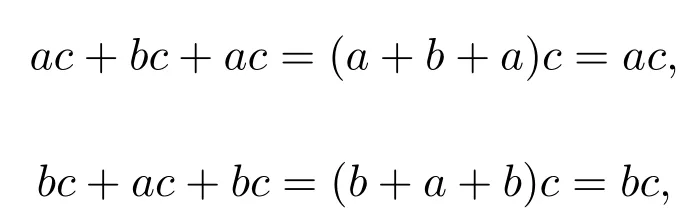
引理 2.2設(shè)則類是S的子半環(huán).
證明若則有a=abn?1,b=ban?1,且

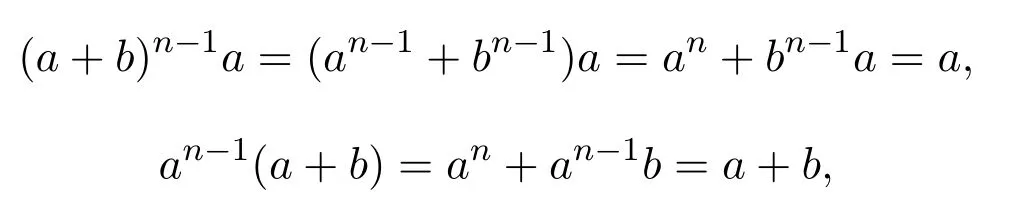
引理 2.3設(shè)則有
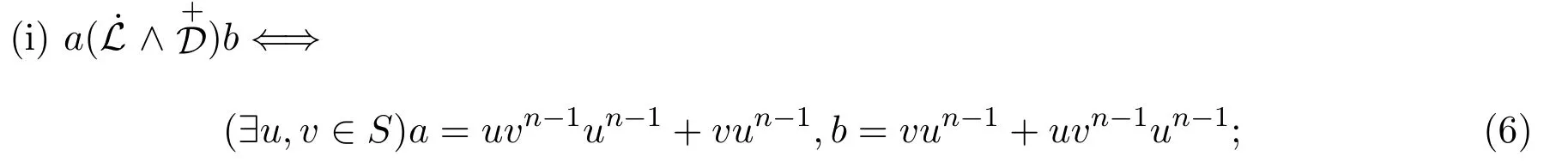
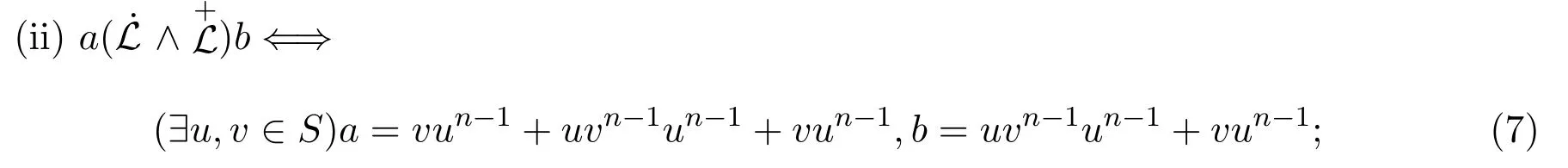
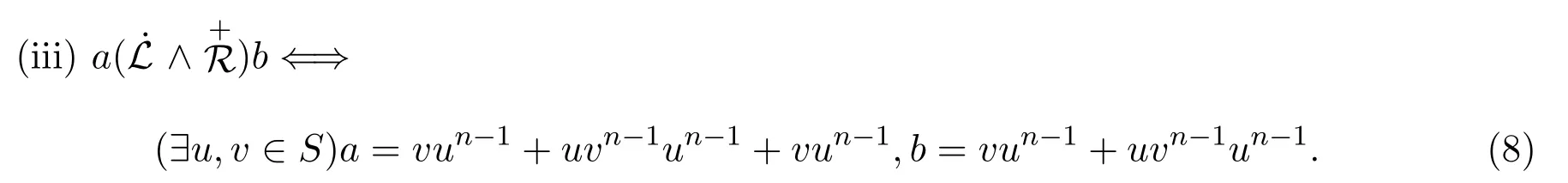
證明(i)若則設(shè) u=a+b,v=b+a,于是有
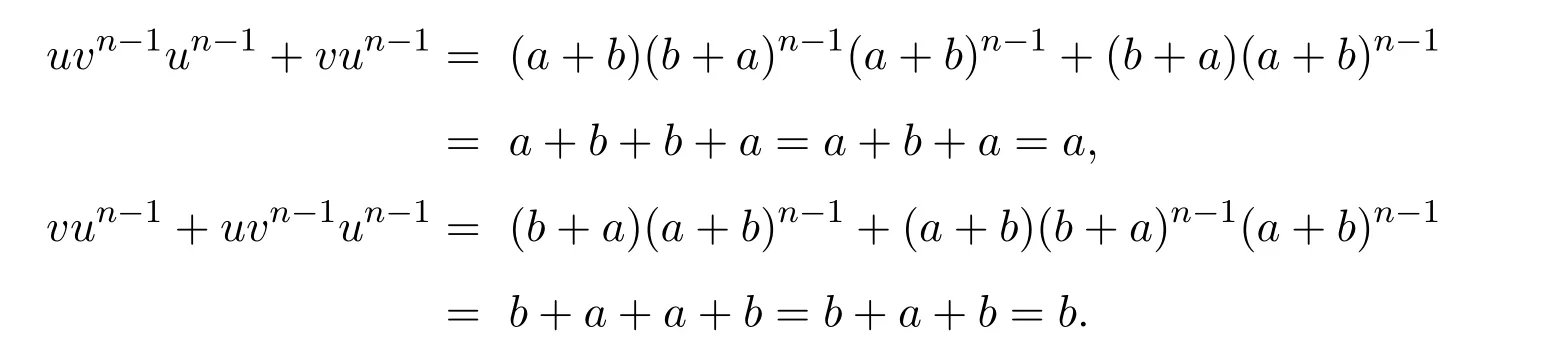
反之,假設(shè)u,v∈S,使得
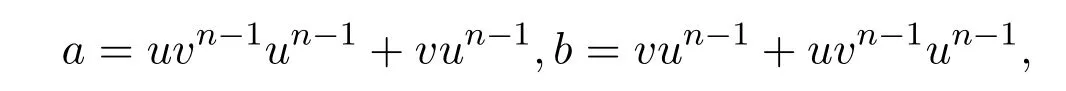
則有
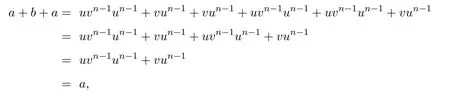
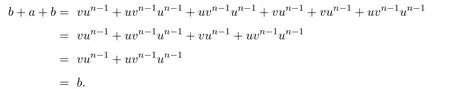
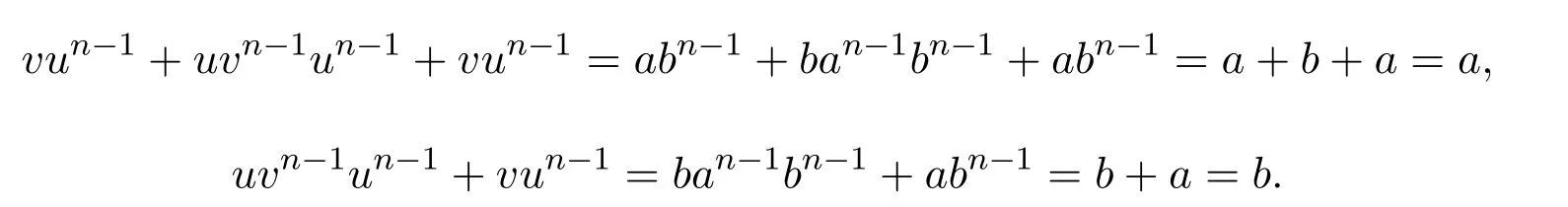
反之,假設(shè)u,v∈S,使得
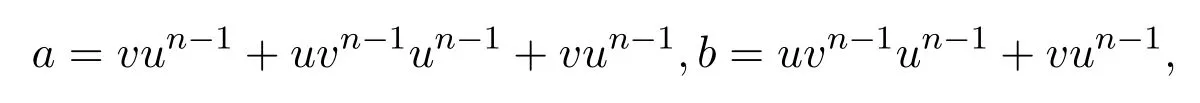
則有
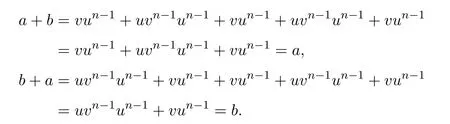
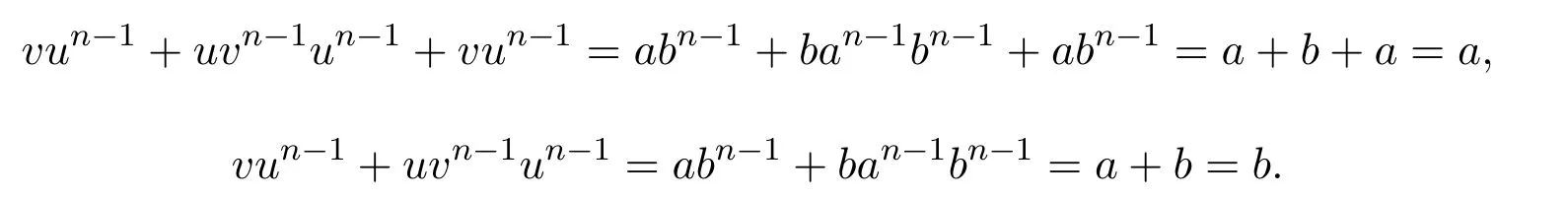
反之,假設(shè)u,v∈S,使得
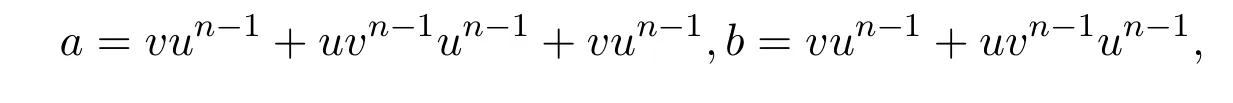
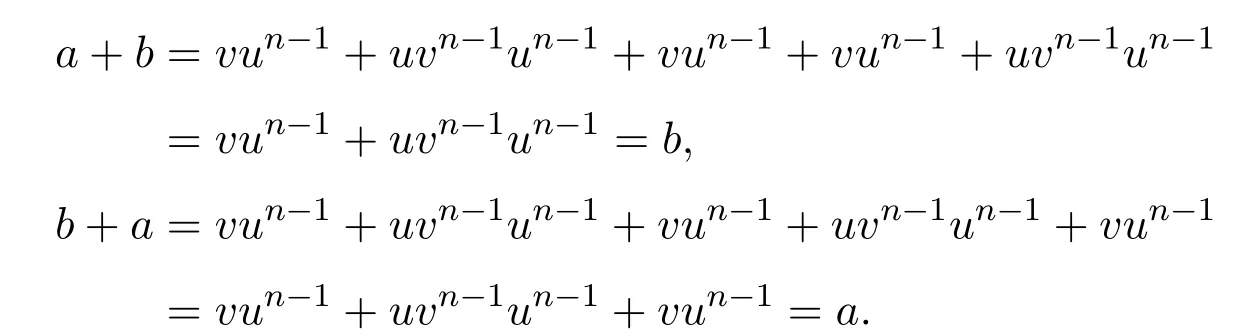
定理 2.1設(shè)則有
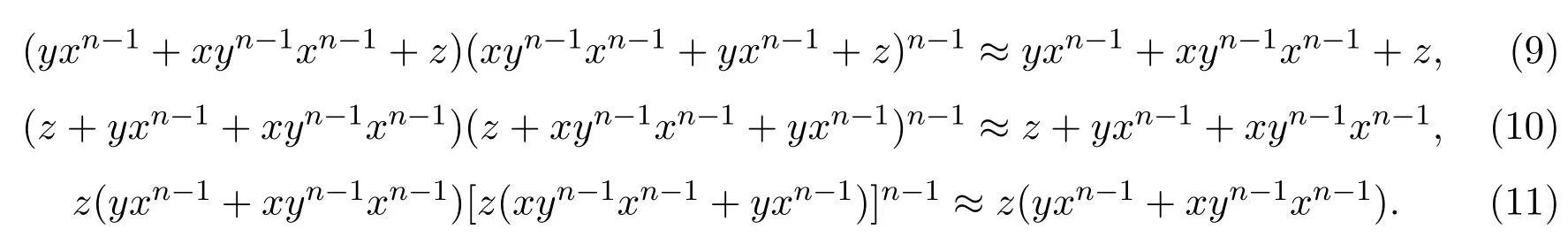

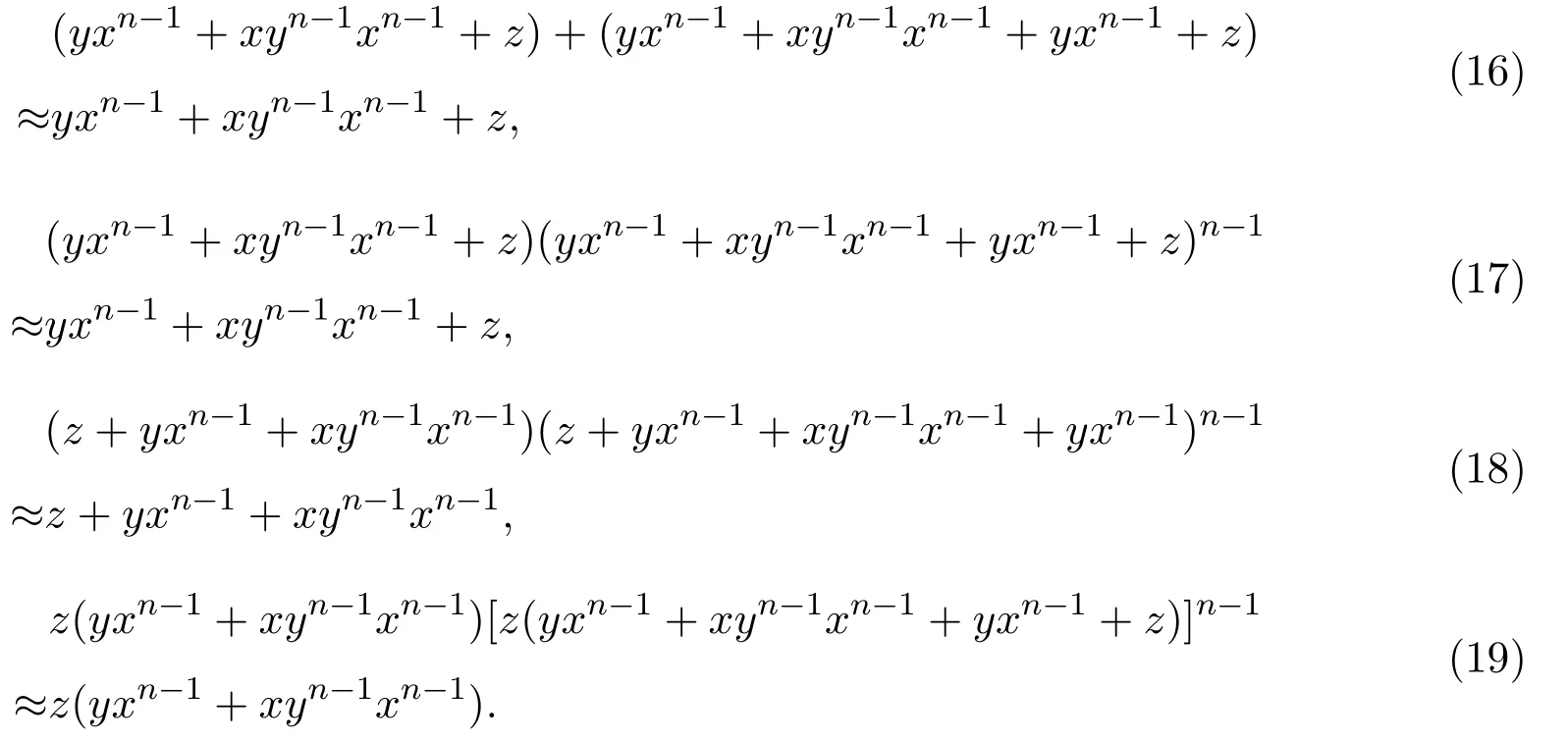
證明只證明 (ii),類似可證(i),(iii).
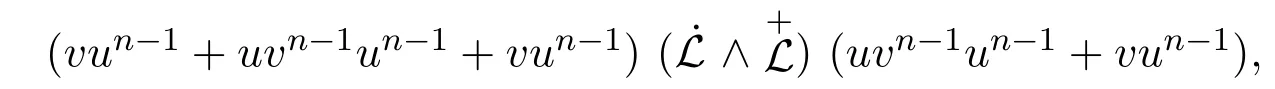
因此對(duì)w∈S,有
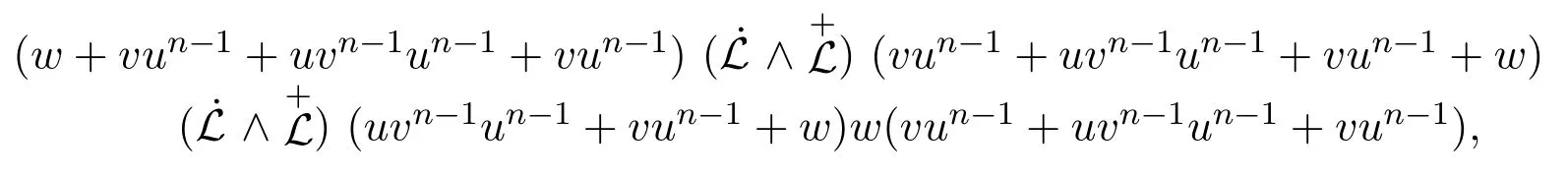
由此可得:
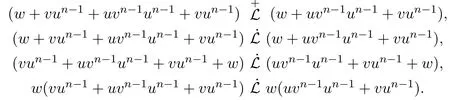
即
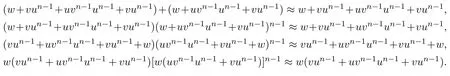
因此可得S滿足等式(12),(13),(14)和(15).
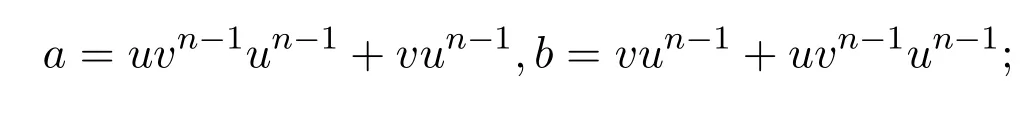
用c代替z,用u代替x,用v代替y,則由(10),(11)式可得:
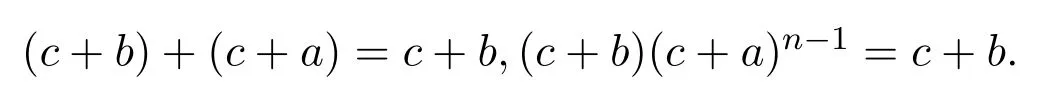
將上式中的a,b交換,類似可得:
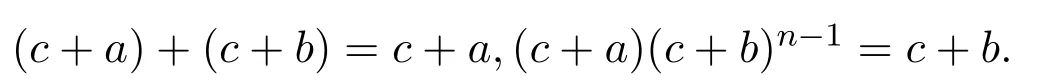
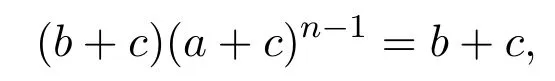
交換a,b有(a+c)(b+c)n?1=a+c.故是(S,+)上的右同余.因此可得是(S,+)上的同余關(guān)系.下證是(S,·)上的同余.已知是(S,·)上的同余關(guān)系,而是(S,·)上的右同余,因此是(S,·)上的右同余.最后證明是(S,·)上的左同余即可.用c代替 z,用u代替 x,用v代替y,由 (15)式可得ca(cb)n?1=ca,交換a,b得cb(ca)n?1=cb,即于是因此也是 (S,·)上的同余.綜上可知是半環(huán)(S,+,·)上的半環(huán)同余關(guān)系.
由引理2.3可知半環(huán)類
引理 2.4設(shè)則有
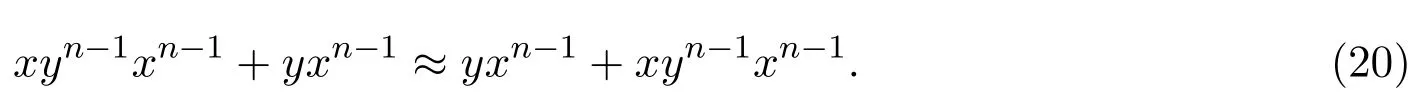
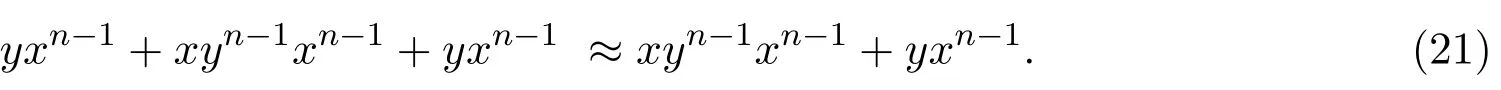
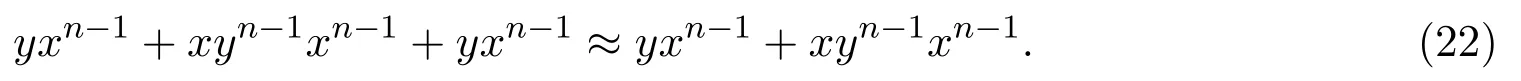
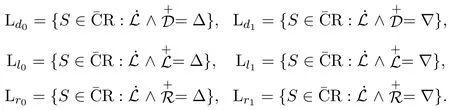
下面將通過Mal′cev積,得到這些半環(huán)簇的Mal′cev積分解.
定理 2.2(i)Ld=Ld1?Ld0;(ii)Ll=Ll1?Ll0;(iii)Lr=Lr1?Lr0.
證明(i)若S∈Ld,則而類在Ld1中,因此在Ld0中,這就說明S∈Ld1?Ld0.即Ld?Ld1?Ld0.
反之,設(shè)S∈Ld1?Ld0且ρ∈Con(S).假設(shè)對(duì)任意的u∈S,ρ-類ρu∈Ld1,則S/ρ∈Ld0.于是由S/ρ∈Ld0和引理2.4(i)可知,對(duì)任意的a,b∈S,
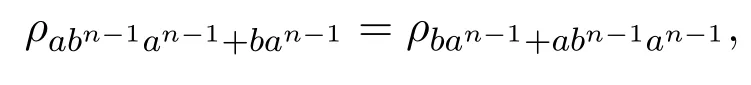
因此對(duì)任意的c∈S,有
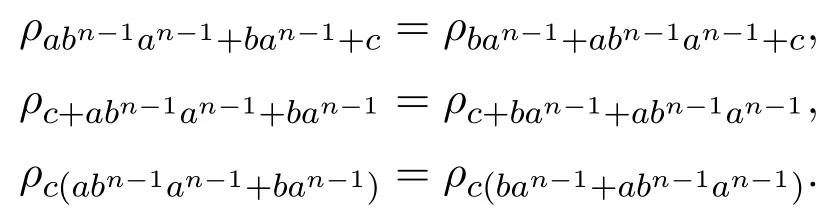
然而,因?yàn)棣製∈Ld1,于是有

因此得到了S滿足等式(9),(10),(11).由定理2.1(i)知S∈Ld,即有Ld1?Ld0∈Ld.綜上證得了 Ll=Ll1?Ll0.
同理可證(ii),(iii).
[1] Petrich M,Reilly N R.Completely Regular Semigroup[M].New York:Wiley,1999.
[2] Howie J M.Fundamentals of Semigroup Theory[M].Oxford:Oxford Science Publication,1995.
[3] Burris S,Sankppanaver H P.A Course in Universal Algebra[M].New York:Springer Verlag,1981.
[4] Pastijn F,Zhao X Z.Green′s D-relation for the multiplicative reduct of an idempotent semiring[J]. Arch.Math.(Brno),2000,36:77-93.
[5] Zhao X Z,Shum K P,Guo Y Q.L-subvarieties of the variety of idempotent semirings[J].Algebra Univers, 2001,46:75-96.
[6] Zhao X Z,Guo Y Q,Shum K P.D-subvarieties of the variety of idempotent semirings[J].Algebra Colloquium, 2002,9:15-28.
[7] Zhao X Z.Idempotent semirings with a commutative additive reduct[J].Semigroup Forum,2002,64:289-296.
[8] Pastijn F,Zhao X Z.Varieties of idempotent semirings with commutative addition[J].Algebra Universalis, 2005,54:301-321.
Several studies of Green′s relations on a class of semiring
Lian Lifeng1,Ren Miaomiao1,Chen Yizhi2
(1.Department of Mathematics,Northwest University,Xi′an 710127,China
2.Department of Mathematics,Huizhou University,Huizhou Guangdong 516007,China)
Green′s-relations of a semiring variety whose additive reduct is band and multiplicative reduct is completely regular semigroup are studied.We give the sufficient and necessary conditions which makebe congruence relations,obtain the classes of semiring which are determined by these Green s-relations are semiring varieties,and through the Mal′cev product,we also obtain the decomposition of these semiring varieties.
semiring,variety,congruence,Green′s relation
O153.3
A
1008-5513(2014)04-0420-08
10.3969/j.issn.1008-5513.2014.04.012
2014-5-21.
廣東高校優(yōu)秀青年創(chuàng)新人才培養(yǎng)計(jì)劃項(xiàng)目(2013LYM0086).
練利鋒(1989-),碩士生,研究方向:代數(shù)學(xué).
2010 MSC:16Y60

