一類后綴碼的代數性質
田徑,胡鋼
(西安理工大學理學院,陜西 西安 710054)
一類后綴碼的代數性質
田徑,胡鋼
(西安理工大學理學院,陜西 西安 710054)
利用自由含幺半群X?上的一個偏序關系,介紹了一類特殊的后綴碼.通過定義這類后綴碼上的兩種二元運算,研究了這類后綴碼的代數性質.證明了該子類在這兩種運算下形成一個加法導出是半格的半環,并且滿足吸收律.從而提供了一個滿足吸收律的半格序半群的例子.
后綴碼;半格序;半環
1 引言與預備知識
設X為非空字符集,稱為字母表.稱X中有限多個字符形成的字符串為X上的字.特別的,稱不含任何字符的字為空字,記為ε.設w為字,記lg(w)為字w中包含字母的個數(同一字母出現多次,按重數計算).若x∈X,則lg(xx)=2.顯然lg(ε)=0.稱由若干字形成的集合(有限或無限)為形式語言(或語言).進一步,記X?為X上字的全體.對任意的x,y∈X?,記xy為字x和y的并置,即:
xy=x1x2···xny1y2···ym,其中x=x1x2···xn,y=y1y2···ym,n,m為正整數.
那么,xy∈X?.易見,并置是X?上的二元運算.這樣X?在并置運算下成為一個幺半群,稱為由X生成的自由幺半群[1],并稱X+=X?{ε}為由X生成的自由半群.
設A?X?是一個非空語言.若對于任意的字x1,x2,···,xn,y1,y2,···,ym∈A,總有成立,則稱A為碼[2].
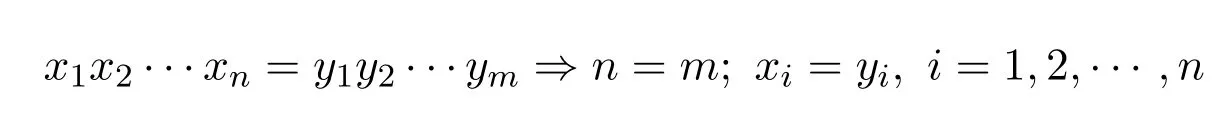
設A?X?是一個非空語言.令w,u∈A.若存在x∈X?使得w=xu,則稱u是w的一個后綴.若A中任意一個字都不是其他字的后綴,則稱A為后綴碼.容易驗證后綴碼是碼[2].
在X?上定義偏序關系“≤s”如下:
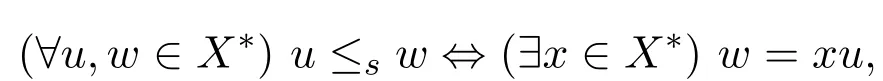
容易發現非空語言A是后綴碼當且僅當A中任意兩個元素在偏序關系“≤s”下是不可比較的.文獻[3]中給出了“≤s”是偏序關系的證明和更多用偏序關系定義的碼.
另一方面,對于一個(2,2)-型代數(T,+,·),如果(T,+)和(T,·)是半群并且滿足分配律,那么就稱(T,+,·)是半環[4].若半環(T,+,·)還適合恒等式x+x≈x和x+y≈y+x,就可以在半群(T,·)上定義一個半格序,使之成為偏序半群.那么二元運算“+”就可以看成取兩個元素的上確界(或下確界).此時,也稱(T,+,·)為半格序半群.由于半格序半群是一種很常見的代數結構,所以被半群學者廣泛研究(見文獻[6-8]).
記S(X)(Sf(X))為字母表X上后綴碼(有限后綴碼)的全體.文獻[3]詳細論述了S(X)作為2-型代數的性質,證明S(X)關于集合的乘法運算“?”成為自由含幺半群,并進一步研究了后綴碼的一些子類和它們的代數性質.文獻[9]利用X?上的嵌入序定義了超碼之間加法運算“+”,使全體超碼在集合乘法和加法的意義下成為半環且適合恒等式1+x≈x.
作為文獻[3,9]的延續,第二節利用X?上的偏序關系得到有限后綴碼的一個子類Sw(X).并討論了它在集合的乘法運算和并運算下的性質.第三節利用集合的乘法運算和并運算定義了這一子類上的兩個新的二元運算—乘法和加法,討論Sw(X)代數性質.結果表明(Sw(X),+,·)是一個滿足吸收律的半格序半群.
2 正規后綴碼
設ρ為X?上的二元關系,H?X?.若對H 中任意兩個不同的元素u,v都有(u,v)/∈ρ,則稱H是X?上ρ的無關集.記X?上所有ρ的無關集形成的集族為Hρ(X).稱X?上的二元關系ρ是嚴格的[10],如果對任意的u,v∈X?有:
(i)uρu且ερu;
(ii)uρv?lg(u)≤lg(v);
(iii)uρv,lg(u)=lg(v)?u=v.
顯然,上一節中提到的二元關系“≤s”是嚴格的并且H≤s(X)=S(X).現定義X?上的二元關系“≤w”如下:
(?u,v∈X?)u≤wv?u=v或(?z∈X+,x,y∈X?)lg(x) 定義2.1設A?X?.若A是X上的≤w的無關集,則稱A是X上正規后綴碼.記X上的全體有限正規后綴碼形成的集族為Sw(X). 由“≤w”的定義可知, 進一步,u≤wv當且僅當下面兩個條件成立: (i)當 lg(u)=lg(v)時,u=v; (ii)當 lg(u) 這樣,容易驗證二元關系“≤w”是嚴格的.此外,由嚴格二元關系定義中的(i)和(iii)知“≤w”是自反的和反對稱的.下面證明“≤w”是傳遞的. 設 t≤wu,u≤wv.若 lg(t)=lg(u)=lg(v),則 t=u=v,那么 t≤wv;若 lg(t)/=lg(u)或 lg(u)/=lg(v),則 lg(t) 性質 2.1“≤w”是X?上的嚴格偏序關系并且≤s?≤w. 證明只需證明 ≤s?≤w.設 u,v∈X?,u≤sv.那么 (?x∈X?)使得 v=xu.故有lg(v)≤lg(u).于是當lg(u)=lg(v)時,由v=xu知x=ε,故u=v.當lg(u) 關于嚴格二元關系,文獻[10]給出了下面的結果. 引理 2.1[10]令ρ1,ρ2是X?上的嚴格二元關系.那么 由性質2.1和引理2.1可知H≤w(X)?H≤s(X).因為H≤s(X)=S(X),所以正規后綴碼是后綴碼.從而Sw(x)?S(X).關于二元關系與碼的聯系的更多內容,參見文獻[3,10]. 例 2.1設X={a,b}.令A={aa,ba,b},B={ba,baa}.由于A是“≤w”無關的,所以A是正規后綴碼.又因為ba≤wbaa,所以B不是正規后綴碼.但B是“≤s”無關的,故B是后綴碼. 設A?X+是非空有限語言.分別記A中所有在偏序關系“≤w”下的極小元和極大元形成的集合為L(A)和U(A),即 根據正規后綴碼的定義可直接得到以下結果. 性質2.2設A?X+是非空有限語言.那么 (i)L(A)和U(A)都是正規后綴碼; (ii)A是正規后綴碼當且僅當L(A)=U(A)=A. 設A?X+.記A中字長最短的元素形成的集合為A,即 性質2.3設A?X+是非空語言.那么是正規后綴碼. 文獻[3]證明如果A和B都是后綴碼,那么A?B也是后綴碼.其中“?”是通常的集合的乘法運算,其定義如下: 但下面的例子表明,對于正規后綴碼,類似的結果一般并不成立. 例2.2設X={a,b}.令A={ab,baa},B={b}.顯然A和B都是正規后綴碼.但A?B={abb,baab}不是正規后綴碼.注意到,集合A∪B={ab,baa,b}甚至不是后綴碼. 引理2.2設那么是正規后綴碼. 證明反證法.假設不是正規后綴碼,則必然存在使a1b1≤wa2b2, 其中a1,a2∈A;b1,b2∈B.若lg(a1b1)=lg(a2b2),則有a1b1=a2b2.因為lg(a1)=lg(a2),所以b1=b2,這與B是正規后綴碼矛盾. 另一方面,若lg(a1b1) 設A,B∈X+.由性質2.3知和是正規后綴碼,又由引理2.2,知是正規后綴碼.進一步,容易證明下面的引理2.3. 引理2.3若A,B∈X+,則 設A,B∈X+.由性質2.2知L(B)是正規后綴碼,又由引理2.2知也是正規后綴碼.并且有 引理2.4若A,B?X+,則 證明設A,B?X+.若則存在使由于是語言中的極小元,那么b是B中的極小元,即b∈L(B).(事實上,若b/∈B,則存在不同于b的b′∈B,使得b′≤wb,于是這就意味著矛盾.)故從而有 關于集合的并運算,有下面的結果. 引理2.5若B,C?X+,則 證明設B,C?X+.顯然L(B∪C)?B∪C,那么 在全體有限正規后綴碼形成的集族Sw(X)上定義乘法運算“·”與加法運算“+”如下: 由于這兩個二元運算都是封閉的,那么(Sw(X),+,·)成為一個(2,2)-型代數.這一節將討論二元運算“·”,“+”的性質并利用相關結果證明(Sw(X),+,·)是一個半環.首先討論乘法運算的性質. 性質3.1設A,B?Sw(X).那么 證明設A,B∈Sw(X).令因為對任意的和b∈B,總有那么所以于是再由引理2.2和性質2.2知故 性質 3.2(Sw(X),·)是半群. 證明只需證明乘法“·”是結合的.對任意的A,B,C∈Sw(X),有 接下來討論加法運算的性質.對于任意的A,B∈Sw(X),根據集合的并運算“∪”的冪等性和交換性得到 這就說明加法運算是冪等的和交換的.進一步,有 性質 3.3(Sw(X),+)是半群. 證明只需證明加法“+”是結合的.對任意的A,B,C∈Sw(X),總有 成立.為了確定集合A∪B∪C在偏序關系“≤ w ”下的極小元.可先找出A∪B中的所有極小元,即L(A∪B).然后再找出集合L(A∪B)∪C中的所有極小元L(L(A∪B)∪C),于是L(A∪B∪C)=L(L(A∪B)∪C)成立.這就說明 同理可證,L(A∪B∪C)=A+(B+C),那么 故“+”是結合的,從而(Sw(X),+)是半群. 為了說明(Sw(X),+,·)是半環,只需再證分配律成立,即對任意的A,B,C∈Sw(X),總有 成立.因為 所以(1)式成立.又因為 所以(2)式成立. 綜上所述,(Sw(X),+,·)是半環并且它的加法導出(Sw(X),+)是半格.此外,還可以證明以下結果. 性質3.4對任意的A,B,C∈Sw(X),有B·A+A=A成立. 證明設A,B,C∈Sw(X).那么 這樣,(Sw(X),+,·)是一個適合吸收律yx+x≈x的半格序半群. [1] Howie J.Fundamentals of Semigroup Theory[M].Oxford:Clarendon Press,1995. [2] Berstel J,Perrin D,Reutenauer C.Codes and Automata[M].Cambridge:Cambridge University Press, 2010. [3] Ito M,J¨urgensen H,Shyr H J,Thierrin G.Out fi x and in fi x codes and related classes of languages[J].Journal of Computer and System Sciences,1991,43(3):484-508. [4] Golan J.The Theory of Semirings,with Applications in Mathematics and Theoretical Computer Science[M]. Harlow:Longman Scienti fi c and Technical,1992. [5] Burris S,Sankappanavar H P.A Course in Universal Algebra[M].New York:Springer-Verlag,1981. [6] Zhao X.Idempotent semigroups with a commutative additive reduct[J].Semigroup Forum,2002,64(2):289-296. [7] Martin K,Libor P.On varieties of semilattice-ordered semigroups[J].Semigroup Forum,2005,71(1):27-48. [8] Sen M K,Bhuniya A K.On semirings whose additive reduct is a semilattice[J].Semigroup Forum, 2011,82(1):131-140. [9] Wang Z,Liang F,He Y,Yang D.Semiring structures of some classes of hypercodes[J].Journal of Automata, Languages and Combinatorics,2009,14(3):259-272. [10] Shyr H J.Lecture notes:Free Monoids and Languages[M].3rd ed.Oxford:Hon.Min.Book Company, 2001. On a subclass of suffix codes Tian Jing,Hu Gang We introduce a subclass of suffix codes in terms of a partially order on X?.By using two binary operations de fi ned on this subclass,we investigate the algebraic properties of it.It is shown that equipped with these two binary operations,this subclass forms a semiring whose addictive reduct is a semilattice.Also,we prove that this algebra satis fi es absorbtion law.Thus,we provide an example of semilattice-ordered semigroup satisfying absorbtion law. suffix codes,semilattice order,semirings O236.2 A 1008-5513(2014)04-0360-07 10.3969/j.issn.1008-5513.2014.04.005 2014-03-20. 國家自然科學基金(51305344);陜西省自然科學基金(2014JQ1014). 田徑(1979-),博士,講師,研究方向:自動機和形式語言理論. 2010 MSC:20M35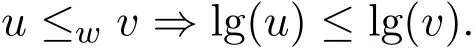

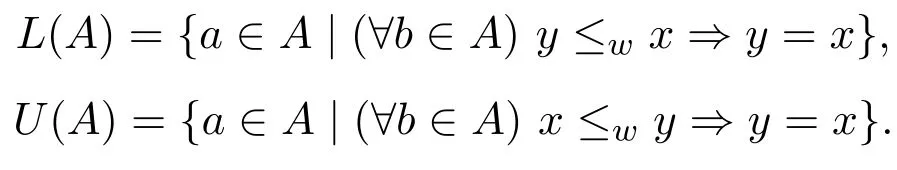

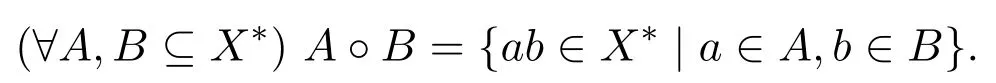
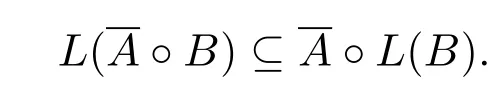
3 正規后綴碼的代數性質
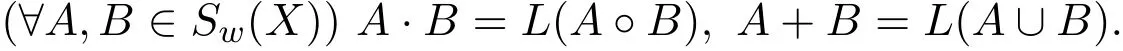

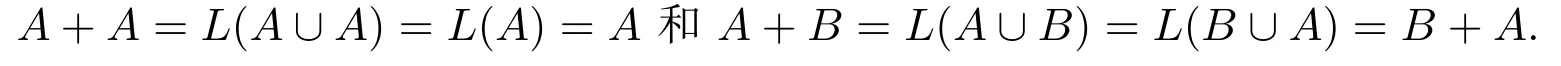

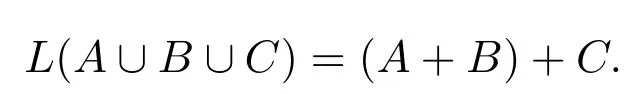
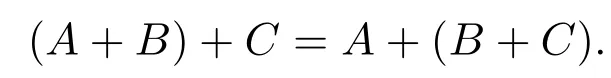
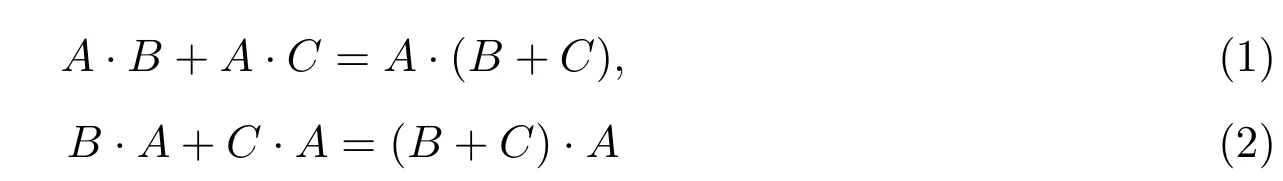
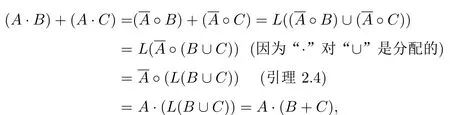


(School of Scince,Xi′an University of technology,Xi′an 710054,China)

