q-Baskakov型算子的A-統計逼近
劉生貴
(嘉應學院數學學院,廣東 梅州 514015)
q-Baskakov型算子的A-統計逼近
劉生貴
(嘉應學院數學學院,廣東 梅州 514015)
引入一類q-Baskakov型算子,對一個非負正則可求和矩陣A,應用A-統計逼近的理論,研究了這類修正的Korovkin型統計逼近性質.對于0 統計逼近;q-Baskakov型算子;連續性模 Baskakov算子在逼近論及其應用中有著重要的地位,它的各種變形也被人們廣泛的研究[14].近年來,因q積分研究的深入,與q積分相關的推廣的Bernstein多項式的研究也開始備受關注. 首先給出文中所需的關于q分析的一些記號.設q>0,對任給非負整數k,q-階乘[k]q!定義如下: 設n,k都是整數,n≥k≥0,q-二項式或Gaussian系數定義為: 記 文獻[5]中,Aral定義一類q-Baskakov算子如下:設n∈N,f∈C[0,∞], 顯然,q=1時算子Bn(f,q;x)即為熟知的Baskakov算子, 若0 定理A對固定的a>0和足夠大的n,設{qn}為滿足的序列,若f∈CM[0,a],則 定理A表明,對任給f∈C[0,1],算子列Bn(f;qn;x)一致收斂于f當且僅當qn=1. 近年來,線性算子的統計逼近被逐步引入逼近論領域[69].把統計收斂的理念引入到逼近論領域大大促進了逼近論的發展,特別是Ces`aro型矩陣可求和方法有力彌補了各類線性算子(例如Hermite-Fej′er插值算子)收斂性質上的不足,因為這些算子在那些簡單的不連續點上并不收斂[1011].A-統計收斂在非收斂正線性算子的求和上顯得更為有效[79]. 設{xn}n∈N是一個數字序列,如果對任給ε>0,有 則稱{xn}n∈N統計收斂于數M.這里?B表示集合B的基數[1213].{xn}n∈N統計收斂于數M記為: 設A=(ajn)是一個無限的可求和矩陣,記x=(xn),如果對每一個j, 收斂,則記關于x=(xn)的A變換為Ax:=(Ax)j.稱矩陣A正則的,如果當時,有(參見文獻[14]). 例如,定義Ces`aro矩陣C1=(cjn)如下: 則C1就是一個正則矩陣.設A是非負可求和的正則矩陣,Freedman和Sember[15]引入了A-統計收斂,它是一種更為一般的統計收斂.稱序列(xn)n∈NA-統計收斂到M,如果滿足對任給ε>0,式子 成立.A-統計收斂到M記為 若將A用單位矩陣代替,則A-統計收斂就是普通意義的收斂.不難看出,如果取 A=C1,則C1-統計收斂就是上面所提到的統計收斂,即對任給的非負的正則矩陣,每一個收斂列A-統計收斂于同一值,但它的逆命題不成立.特別,Kolk[16]已經證得,當非負正則矩陣A=(ajn)滿足條件時,A-統計收斂強于普通意義的收斂. 本文定義一類q-Baskakov型算子如下.設0 將研究這類新算子A-統計逼近的性質.借助光滑模,討論A-統計逼近收斂速度的估計.進一步證明,這類q-Baskakov型算子算子的收斂速度要優于算子 先給以下兩個引理. 引理 2.1設n∈N,0 證明由下面的等式 通過簡單計算可得(4)式成立. 另一方面,因為 所以 為了方便,本文中記I:=[0,∞),C(I):={f:f為在區間I上的連續的實值函數}, ? CB(I):={f:f為I上的有界連續函數}.空間Hω是定義在區間I上且滿足 的實值函數f所組成的集合.其中ω為如下定義的連續模.設f∈C(I),任給δ>0, 顯然Hω中的函數在I中連續且有界. 引理2.2 [17]設A=(ajn)是一個非負可求和的正則矩陣,{Ln}是從Hω到CB(I)的正線性算子序列,則對任意f∈Hω,有 如果滿足 定理2.1設A=(ajn)是一個非負正則可求和矩陣,{qn}是一個在區間(0,1]上的序列,且滿足 則對任意f∈Hω,有 證明由(4)式,有 對給定的ε>0,定義如下集合: 由(10)式知S?S?,則對每一個j∈N,有 在(10)式中令j→∞,并注意到(8)式,有 則 最后,由(6)式,可得 由(8)式,有 定義如下集合: 得U?U∪U.因此,對所有j∈N,有 12 令j→∞,可得 由引理2.2,及(9),(11)和(13)式,命題得證. 注 2.1事實上,可以構造序列{qn}滿足(8)式.例如,設 顯然A=(ajn)是一個正則矩陣.對α>1,定義序列{qn}如下: 則有stA?limnqnn=1,但是序列{qnn}在普通意義下并不收斂.另一方面,若n/=m2,則不難得出 引理 3.1對n∈N,0 其中ei(t)=ti,i=0,1,2.由光滑模的性質,對λ,t>0,ω(f,λt)≤(1+λ)ω(f,t)得 證明由(7)式易得(15)式.下面證明(16)式. 最后,由等式[k]2q=[k]q(q[k?1]q+1)可得, 注3.1顯然,由引理3.1,若 則 定理 3.1設n∈N,f∈Hω,{qn}是一滿足0 其中 證明因為算子是正線性算子,對任給x∈[0,∞),有 由(14)式,對任意δ>0,有 由正線性算子的Cauchy-Schwarz不等式,可得 由(15)-(17)式,得 注3.2若{qn}滿足(8)式,有 [1]Xiaoming Z,Gupta V.Rate of convergence of Baskakov-B′ezier type operators for locally bounded functions[J].Comput.Math.Appl.,2002,44:1445-1453. [2]Gupta V,Yadav R.Rate of convergence for generalized Baskakov opoerators[J].Arab J.Math.Scineces, 2012,18:39-50. [3] Jes′us D L C,Francisco L.Approximating Sz′asz and Gamma operators by Baskakov opertors[J].J.Math. Anal.Appl.,1994,184:585-593. [4] Aral A,Gupta V.Generalized q-Baskakov operators[J].Math.Slovaca,2011,61:619-634. [5] Aral A,Gupta V.On q-Baskakov type operators[J].Demon.Math.,2009,XLII(1):109-122. [6] Boos J.Classical and Modern Methods in Summability[M].Oxford:Oxford Univ Press,2000. [7] Gadjiev A,Orhan C.Some approximation theorems via statistical convergence[J].Rocky Mountain J. Math.,2002,32:129-138. [8] Do?gru O,¨Orkc¨u M.Statistical approximation by a modi fi cation of q-Meyer-K¨onig and Zeller operators[J]. Appl.Math.Letters,2010,23:261-266. [9] Dalmanoglu O,Dogru O.On statistical approximation properties of Kantorovich type Bernstein operators[J]. Math.Comput.Modelling,2010,52:760-771. [10] Bojanic R,Khan M.Summability of Hermite-Fej′er interpolation for functions of bounded variation[J].J. Natur.Sci.Math.,1992,32:5-10. [11] Bojanic R,Cheng F.Estimates for the rate of approximation of functions of bounded variation by Hermite-Fej′er polynomials[J].CMS Conf.Proc.,1983,3:5-17. [12] Ilinskii A,Ostrovska S.Convergence of generalized Bernstein polynomials[J].J.Approx.Theory,2002,116:100-112. [13] Do?gru O,¨Orkc¨u M.Statistical approximation by a modi fi cation of q-Meyer-K¨onig and Zeller operators[J]. Appl.Math.Letters,2010,23:261-266. [14] Videnskii V.On some classes of q-parametric positive linear operators[J].Oper.Theory Adv.Appl.,2005, 158:213-222. [15] Freedman A,Sember J.Densitied and summability[J].Paci fi c J.Math.,1981,95:293-305. [16] Kolk E.Matrix summability of statistically convergent sequences[J].Analysis,1991,13:77-83. [17] Erkus E,Duman O.A-statistical extension of the Korovkin type approximation theorem[J].Proc.Indian Acad.Math.Sci.,2005,115(4):499-508. A-statistical approximation of q-Baskakov type operators Liu Shenggui In this paper,the q-Baskakov type operators are introduced.And we investigate the Korovkin type statistical approximation properties of these operators via A-statistical approximation.For 0 statistical approximation,q-Baskakov type operators,modulus of continuity 0174.41 A 1008-5513(2014)04-0367-10 10.3969/j.issn.1008-5513.2014.04.006 2013-12-17. 國家自然科學基金(11001107). 劉生貴(1974-),碩士,講師,研究方向:函數逼近論. 2010 MSC:41A10,41A361 引言

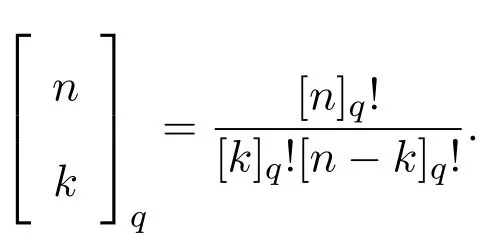
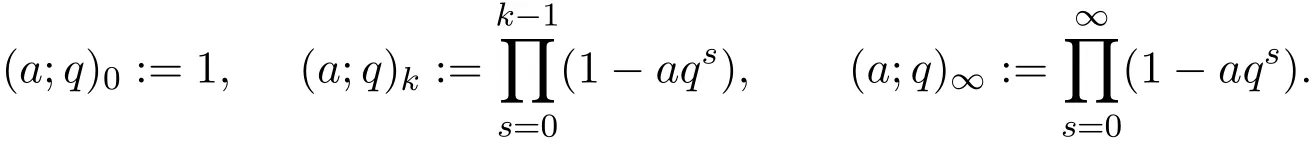
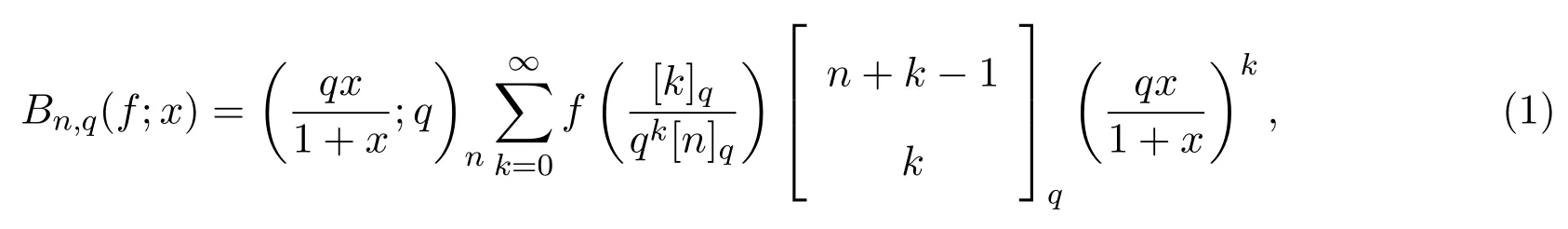
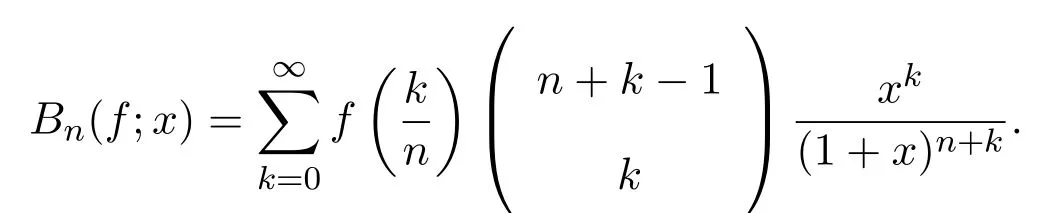
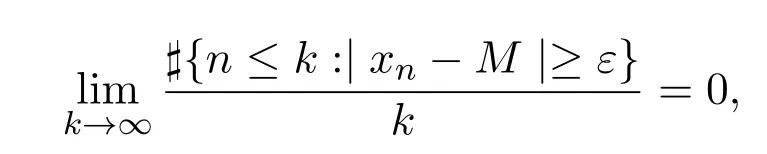
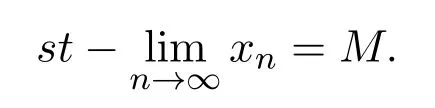
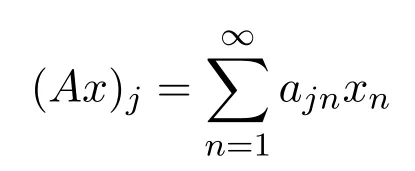
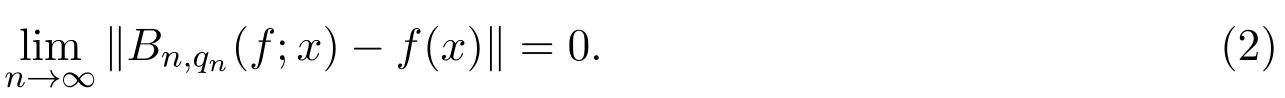

2 算子的A-統計逼近
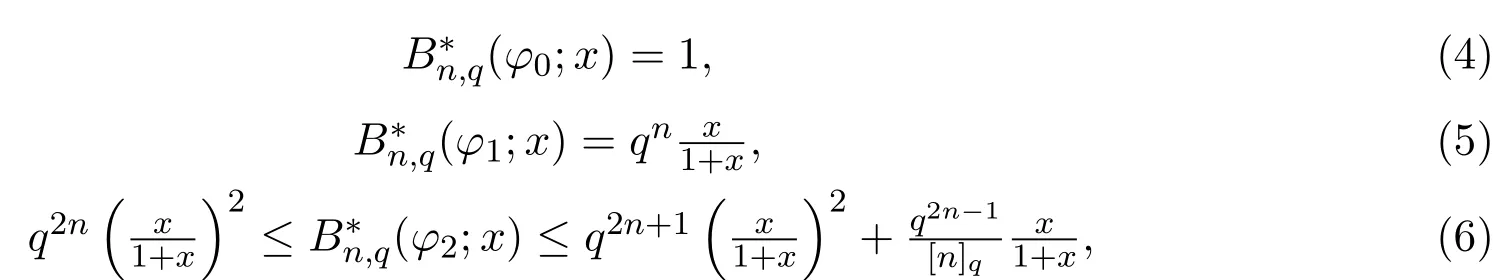
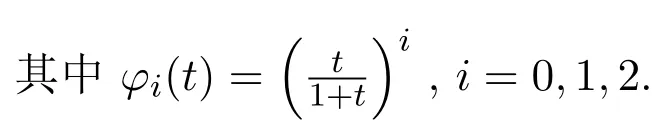
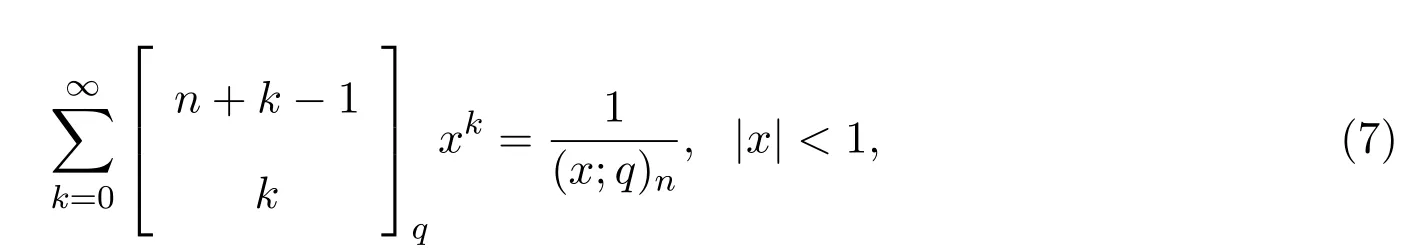
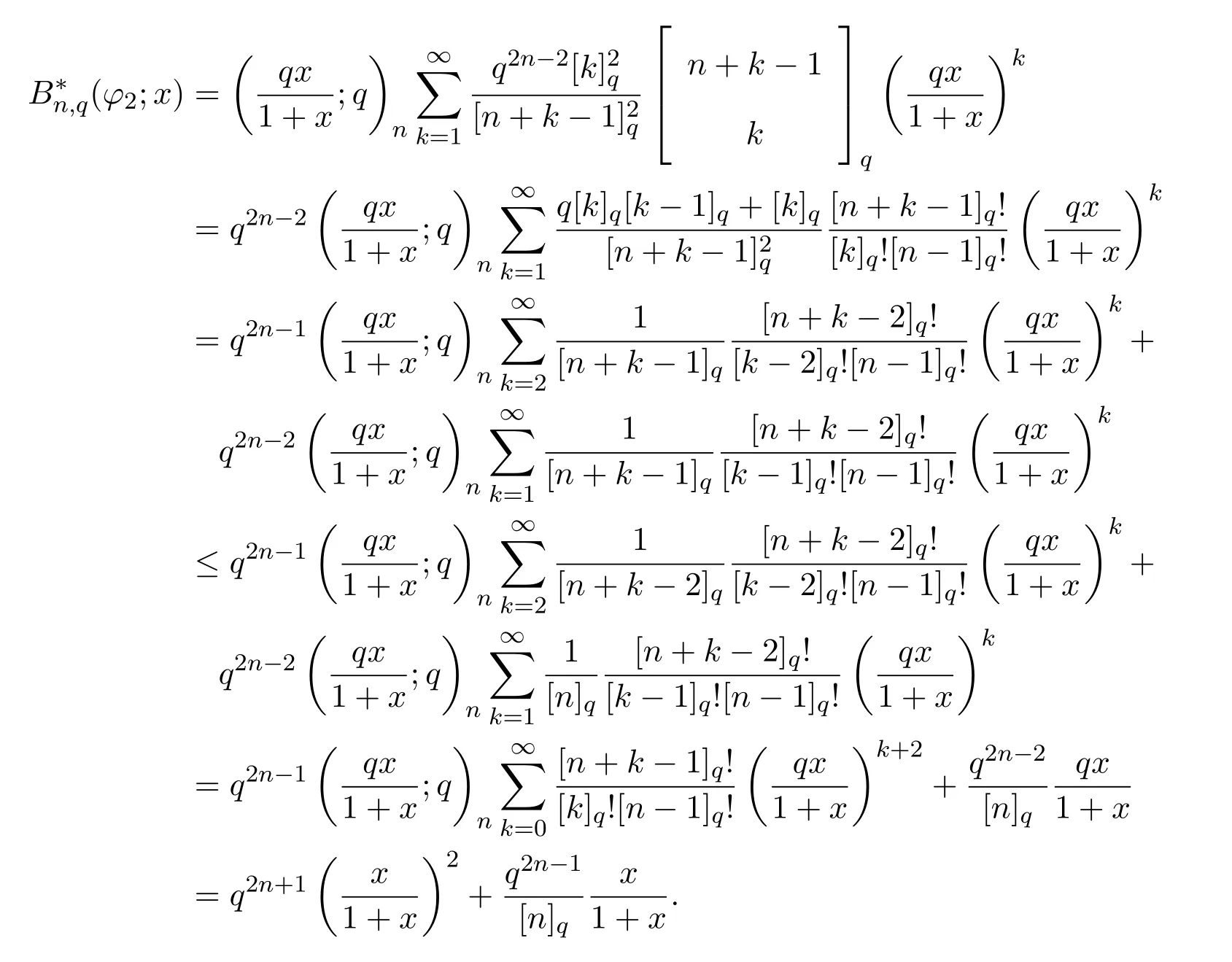
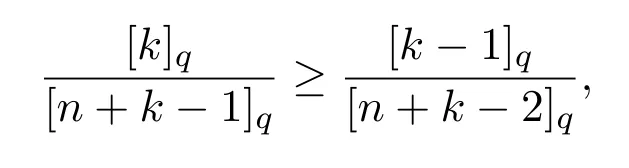
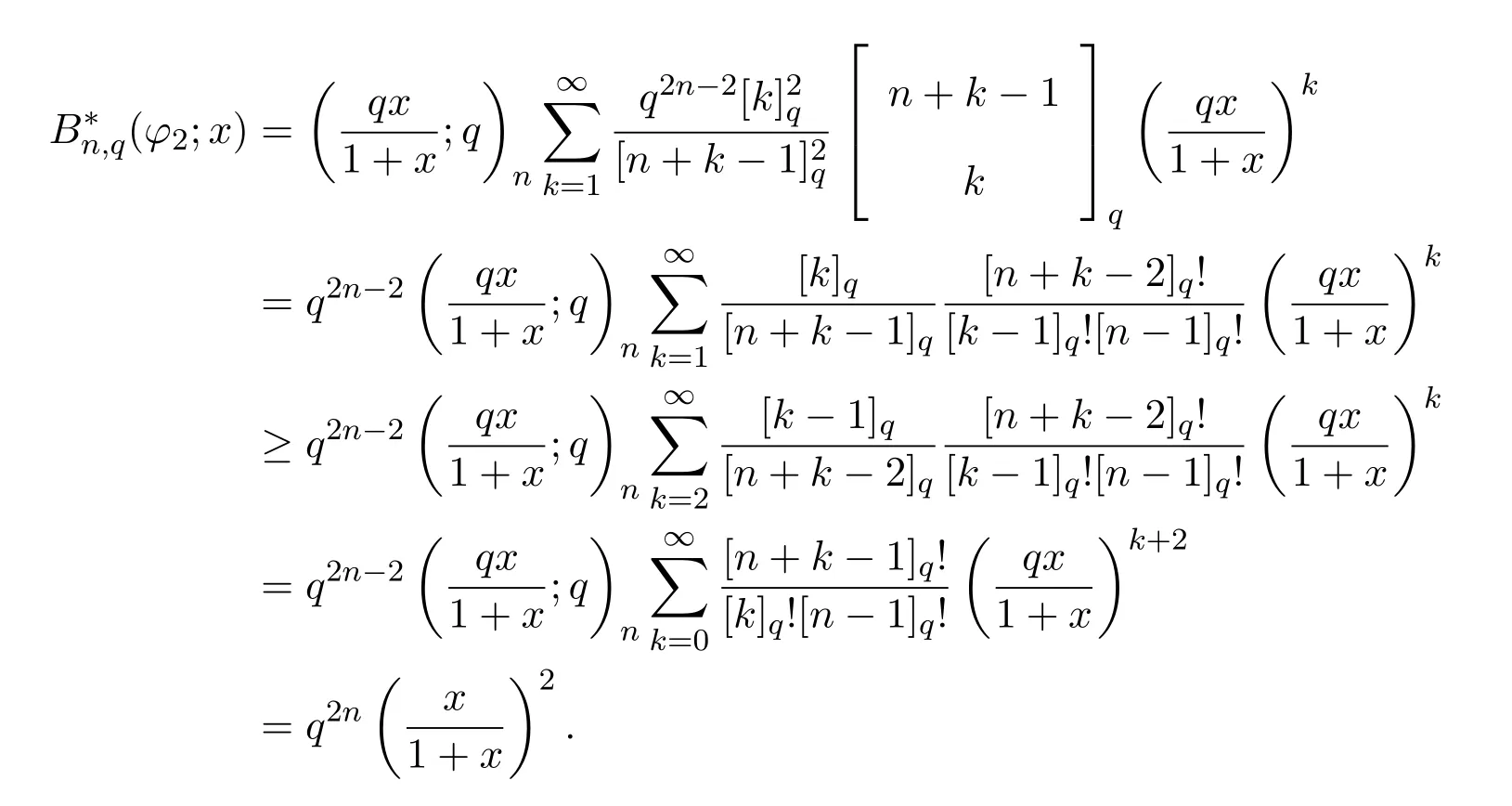
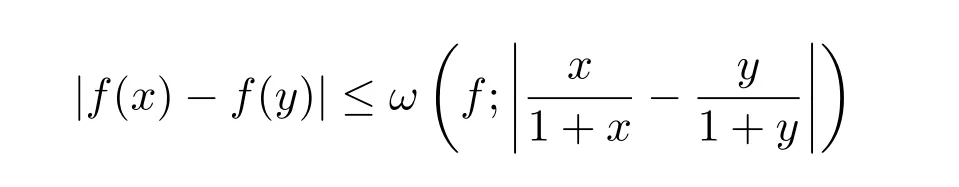
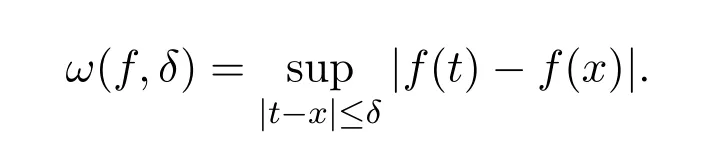
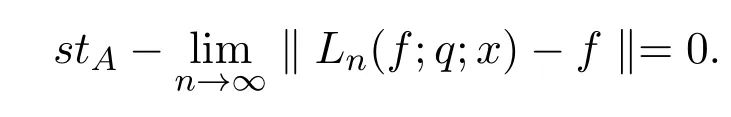
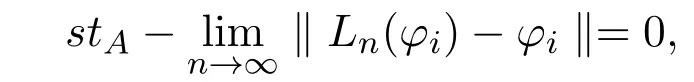
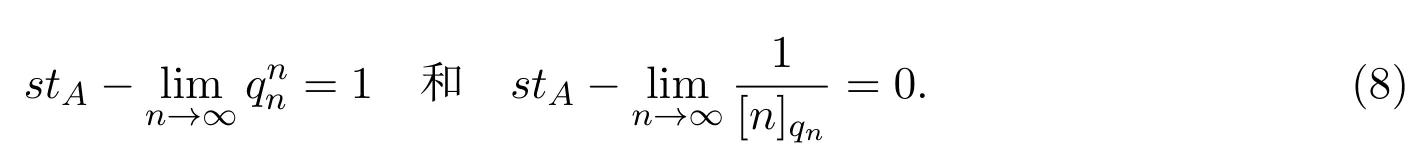
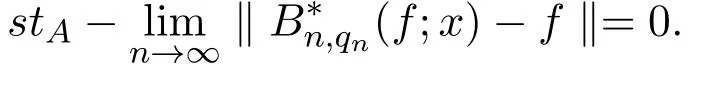
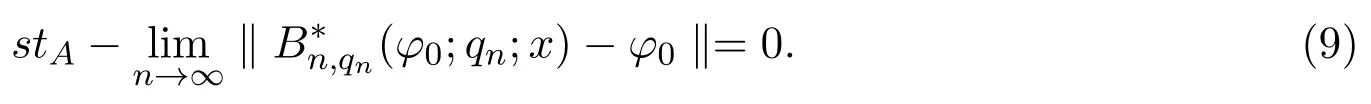
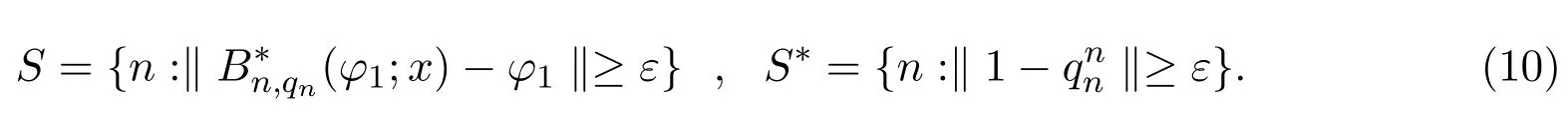
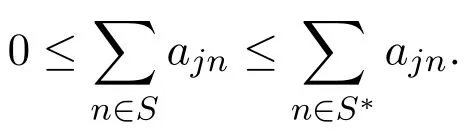
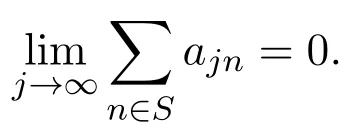
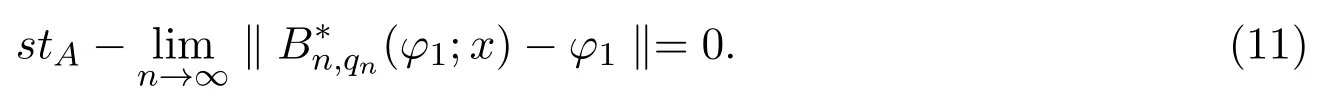
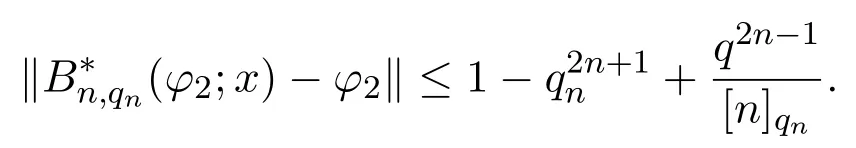
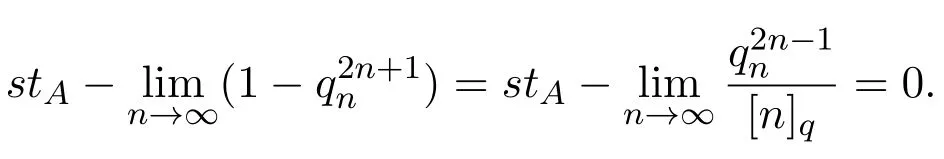
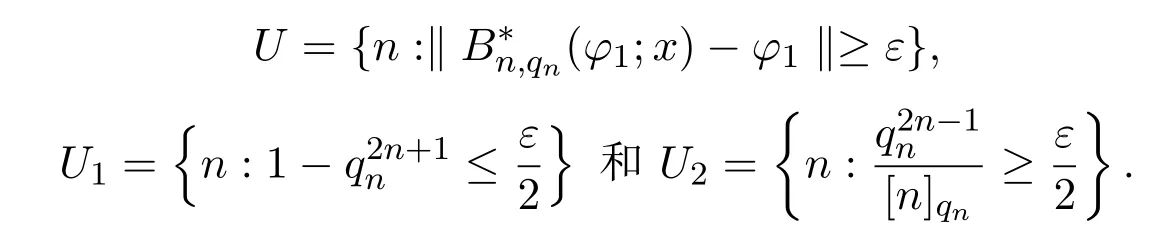
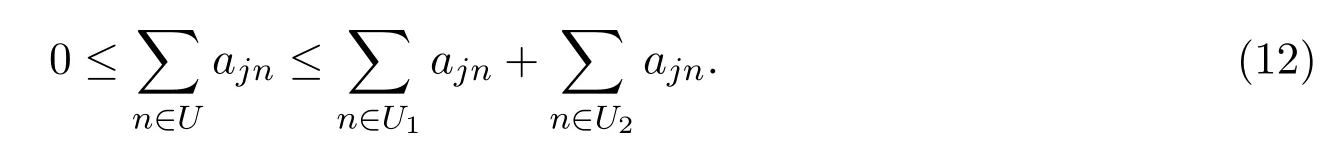
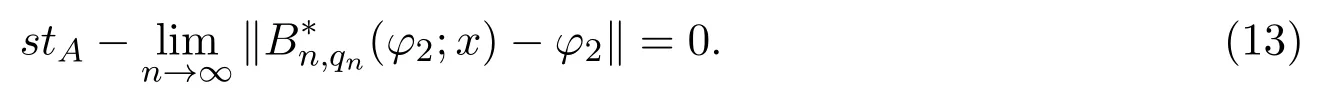
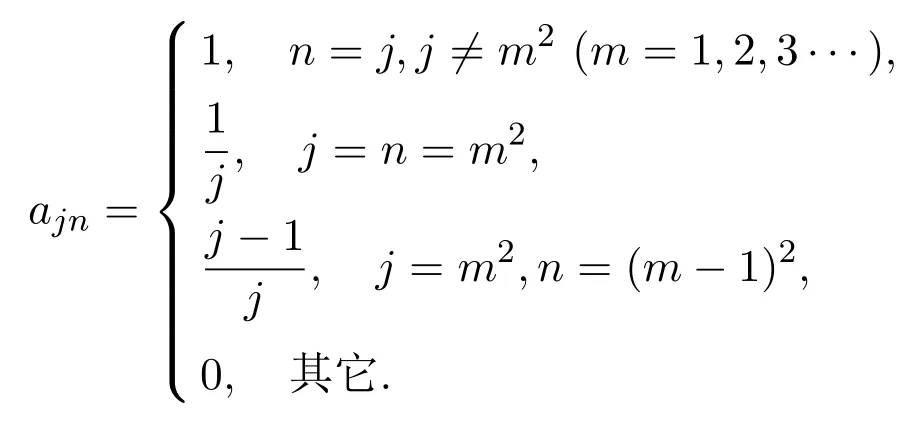
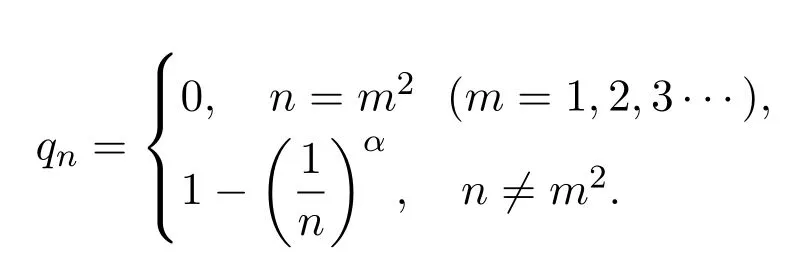
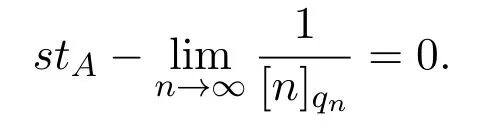
3 A-統計逼近的收斂速度估計
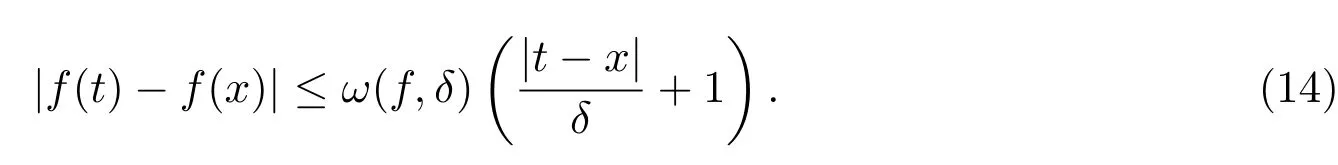


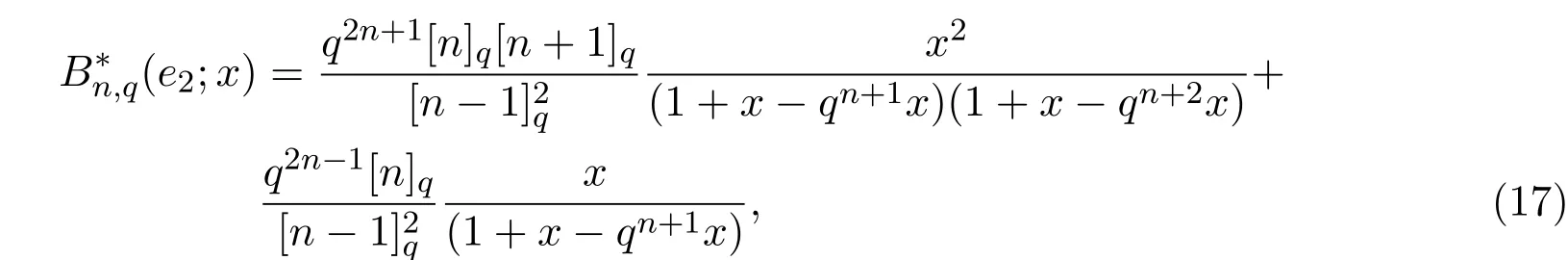
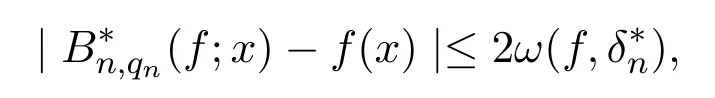
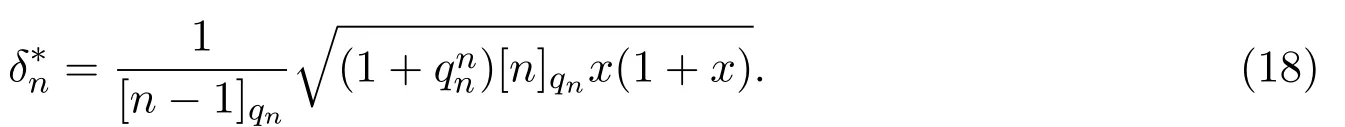

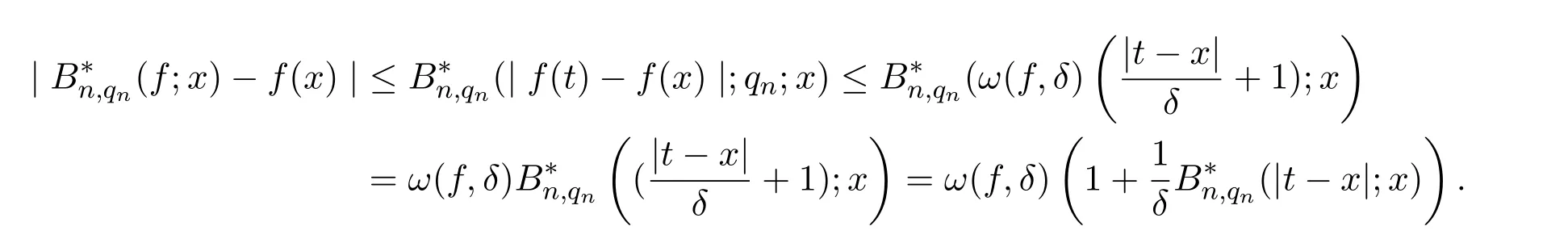
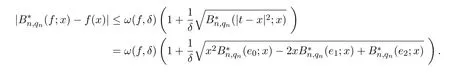

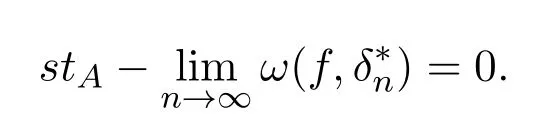
(School of Mathematics,Jiaying University,Meizhou 514015,China)

