基于高速單體無人艇航行性能的并行優化方法

俞 強，楊松林，王保明，于 寧

(1.江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003；2.南京中船綠洲機器有限公司，江蘇 南京 210012)

基于高速單體無人艇航行性能的并行優化方法

俞 強1，楊松林1，王保明1，于 寧2

(1.江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003；2.南京中船綠洲機器有限公司，江蘇 南京 210012)

基于高速單體無人艇航行性能建立包括快速性、操縱性和耐波性的綜合優化數學模型，構造混合的遺傳混沌算法(GAPCA)和混沌遺傳算法(PCAGA)，并編制相關軟件對該模型進行綜合優化計算，探討混合算法和單一算法(遺傳算法(GA)和混沌算法(CA))優化性能的優劣，同時研究二次載波搜索域區間比例和區間并行次數對優化效率的影響，得到遺傳混沌優化算法和混沌遺傳優化算法相比單一優化算法尋優效率高，不同算法對應于不同的最佳二次區間搜索比例。

水面無人艇；航行性能；綜合優化；遺傳混沌算法；混沌遺傳算法

0 引 言

船舶優化設計是一個涉及多學科多領域多目標的綜合設計優化問題，這種尋找最優設計過程中往往需要對變量的可行域進行大量搜索[1]。近年來遺傳算法和混沌算法在船舶工程優化問題得到了一定的應用，國內有馮佰威結合國外艦船研制領域中多學科優化的典型應用，提出了適合我國艦船研制模式的計算環境體系結構[2]。唐正茂等對船舶概念設計階段進行了多學科和多目標優化研究[3]。但隨著設計考慮因素增多帶來設計變量的不斷增加，優化耗費的時間會呈現指數倍增長，為了提高優化效率，本文基于高速單體無人艇航行性能綜合優化問題，提出了一種基于遺傳算法和混沌算法的并行混合優化方法。

1 基于遺傳和混沌的并行優化方法

1.1 遺傳算法與混沌算法

1)遺傳算法(GA)

遺傳算法是建立在自然選擇和群體遺傳學基礎上，通過自然選擇、雜交和變異實現搜索的方法進行優化，遺傳算法對于變量較少的多目標工程設計優化問題尋優的能力很強，但隨著種群規模的不斷增加，進行同樣代數，遺傳算法的效率會大大降低，遺傳算法的具體步驟如下：

步驟1 確定種群中個體個數，遺傳代數，交叉概率和變異概率，初始化種群；

步驟2 通過適應度函數計算種群中個體的絕對適應度，并根據其對個體進行排序，適應度函數為懲罰函數和目標函數的乘積，目標函數是指尋優指標函數，懲罰函數為設計約束的滿足程度，懲罰函數的構造策略是基于約束的重要程度構造懲罰因子；

步驟3 通過個體的絕對適應度計算相對適應度和累加適應度，利用輪盤賭方法，優勝劣汰，對種群中個體進行更新，形成新的種群；

步驟4 對種群中的個體進行交叉，交叉方法采用非對稱交叉方法，對種群中較差的個體進行變異得到新的個體基因，增加種群得到最優個體的概率，重復步驟2。

2)混沌算法(CA)

混沌優化算法通過混沌變量來實現，最常用的是基于logistic映射混沌優化方法。

步驟1構造混沌因子，選取一個X0，取值為0～1之間的數，但是不能等于0.25，0.5，0.75，(混沌奇點)，帶入logistic模型進行初值映射：

xn+1=μxn(1-xn)。

(1)式中μ為控制參數。不難證明，當μ等于4時處于完全混沌狀態，利用混沌對初值的敏感特性，迭代得到多個0～1之間不同初值，稱為混沌因子。

步驟2 將混沌變量的值映射到設計變量的空間得到相應自變量的N維向量(N為自變量的個數)：

xi=ai+ui(bi-ai)，

Xj:Xj={x1,x2,x3,…,xN}→f(Xj)。

式中：i取值范圍為1～N；j取值為1～M，M為混沌優化代數。

1.2 基于并行因子的并行算法

傳統的優化算法都是對于自變量區間區域整體進行尋優，在自變量個數比較少的情況下，尋優能力比較可觀。隨著自變量個數增加，尋優能力會大大降低，因此借用計算機學科中并行的思想將設計變量的區間進行等區域劃分，每個自變量的區域被分成幾個區間塊，各個自變量區間塊的組合形成一個計算向量空間，假設設計變量的個數為N，劃分的區間次數(又稱為區間并行次數)為M，每個區間組合中優化計算次數為P，則形成區間的組合為MN方式，總的計算次數W：

W=MNP。

(2)

優化的區域本來是一個N維空間，并行算法實質是對區間的等區域分割，將計算空間進行縮小，因此能大大提高尋優的概率。由于計算的區間向量空間是并行次數的指數函數，所以區間并行次數不是越多越好，合理的選擇區間并行次數和每個區間組內的尋優次數是決定并行算法優劣的關鍵。

借用計算機中數制編碼的思想，在程序中引入并行因子的概念，設置并行因子的初值為0000000....00(0的個數為N)，讓其最低位的0以1的步長進行遞增，當某個位上的數達到M則需要向高位進1，同時該位的數重新設置為0，典型的例如并行次數為2時，并行因子進行的是二進制的N位自增運算，一般情況下并行因子的設置與自變量的個數和每個區間組的尋優次數有關，一般選取不會超過4，否則并行算法的尋優優勢不能體現?；诓⑿兴惴ㄌ岢鱿旅?種算法：

1)混沌并行算法(PCA)：基于并行思想每個區間組中采用混沌算法進行尋優。

2)混沌二次并行算法(PDCA)：第一次載波采用區間的并行混沌算法，第二次在第一次選取的4個最優解的一定鄰域進行非并行的二次載波，尋取最優解。

3)遺傳并行算法(PGA)：基于并行思想每個區間組中采用遺傳算法進行尋優

4)遺傳二次并行算法(PCA)：第一次載波采用區間的并行遺傳算法，第二次在第一次選取的4個最優解的一定鄰域進行非并行的二次載波，尋取最優解。

5)混沌遺傳算法(PCAGA)：第一次載波采用混沌并行算法，第二次載波采用遺傳非并行算法，在第一次5個最優解的一定鄰域內尋取最優解。

6)遺傳混沌算法(GAPCA)：第一次載波采用非并行遺傳算法，第二次載波采取并行的混沌算法，在第一次5個最優解的一定鄰域內尋取最優解。

2 高速單體無人艇航行性能綜合優化模型

2.1 設計變量

綜合快速性、操縱性、耐波性的設計變量，本文中高速單體船流體動力學性能綜合優化的數學模型選擇17個船型參數作為設計變量，分別是：船長L，船寬B，吃水T，方型系數CB，中橫剖面系數CM，設計水線面系數CW，浮心縱向位置LCB，螺旋槳直徑DP，盤面比AE/AO，螺距比P/DP，螺旋槳轉速N，設計航速VS，半進水角ie，尾板相對浸濕面積At/Am，縱傾角α，斜升角β，重心距基線高度Zg，將其用向量X表示，即：

X= {X1,X2,X3,X4,X5,X6,X7,X8,X9,X10,X11,

X12,X13,X14,X15,X16,X17}={L,B,T,CB,

CM,CW,LCB,DP,AE/AO,P/DP,N,VS,ie,

At/Am,α,β,Zg}。

(3)

2.2 目標函數

高速單體水面無人艇航行性能的總目標函數用F(X)表示如下：

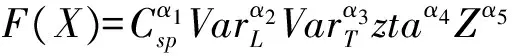
(4)

式中α1，α2，α3，α4，α5分別為快速性、直線穩定性、回轉性、縱搖和垂蕩指標的權重，并將該指標壓縮至0～1之間標準值，且有α1α2α3α4α5=1。

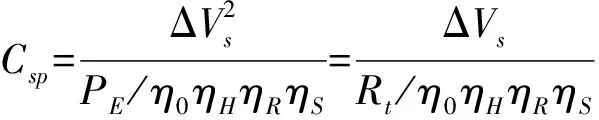
(5)

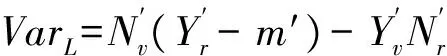
(6)

VarT=D/L。

(7)

借助于Fridsma圖譜進行四維插值得出縱搖和垂蕩十分之一有義幅值ψ1/10和Z1/10。

2.3 約束條件

1)等式約束

① 滿足浮性條件，Δ保持不變，Δ-LBTCB=0；

② 螺旋槳的推力與船舶航行時遭受的阻力平衡；

③ 設計狀態下主機供給螺旋槳的轉矩必須等于螺旋槳吸收的轉矩。

2) 不等式約束

① 各個設計變量的設計取值范圍；

② 按海船穩性規范，初穩性高GM,GM>0.7mg；

③ 螺旋槳需滿足空泡要求；

⑤ 橫搖幅值Φα滿足不等式約束條件：Φα=Φα(X)≤10°。

⑦ 滿足舒適性條件(主要考慮橫搖周期大小)：Tφ=Tφ(x)>2.0 s。

3 優化計算及結果分析

3.1 優化計算

高速單體無人艇的航行性能綜合優化問題涉及到17個設計變量，包括6個等式約束和7個不等式約束，本文基于此數學模型和上述6種算法基礎上編寫了計算程序。該高速艇優化設計變量的取值范圍如表1所示。

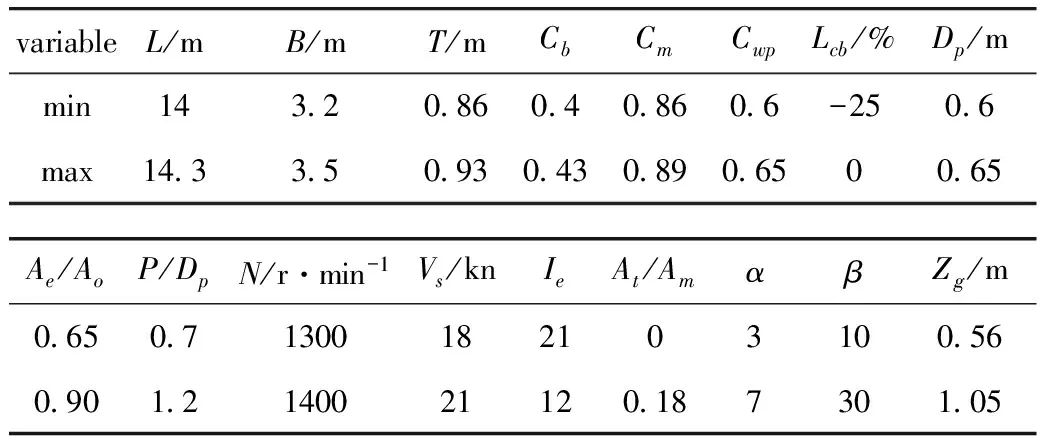
表1 設計變量范圍

選取α1=9/7，α2=1，α3=7/9，α4=1，α5=1，這樣的選取原則是考慮到高速單體船的快速性、操縱性、耐波性的相對重要性來決定的[4-5]，本文在1臺計算主頻為2.3GHz，內存為2G，硬盤為250G的電腦上進行優化計算。

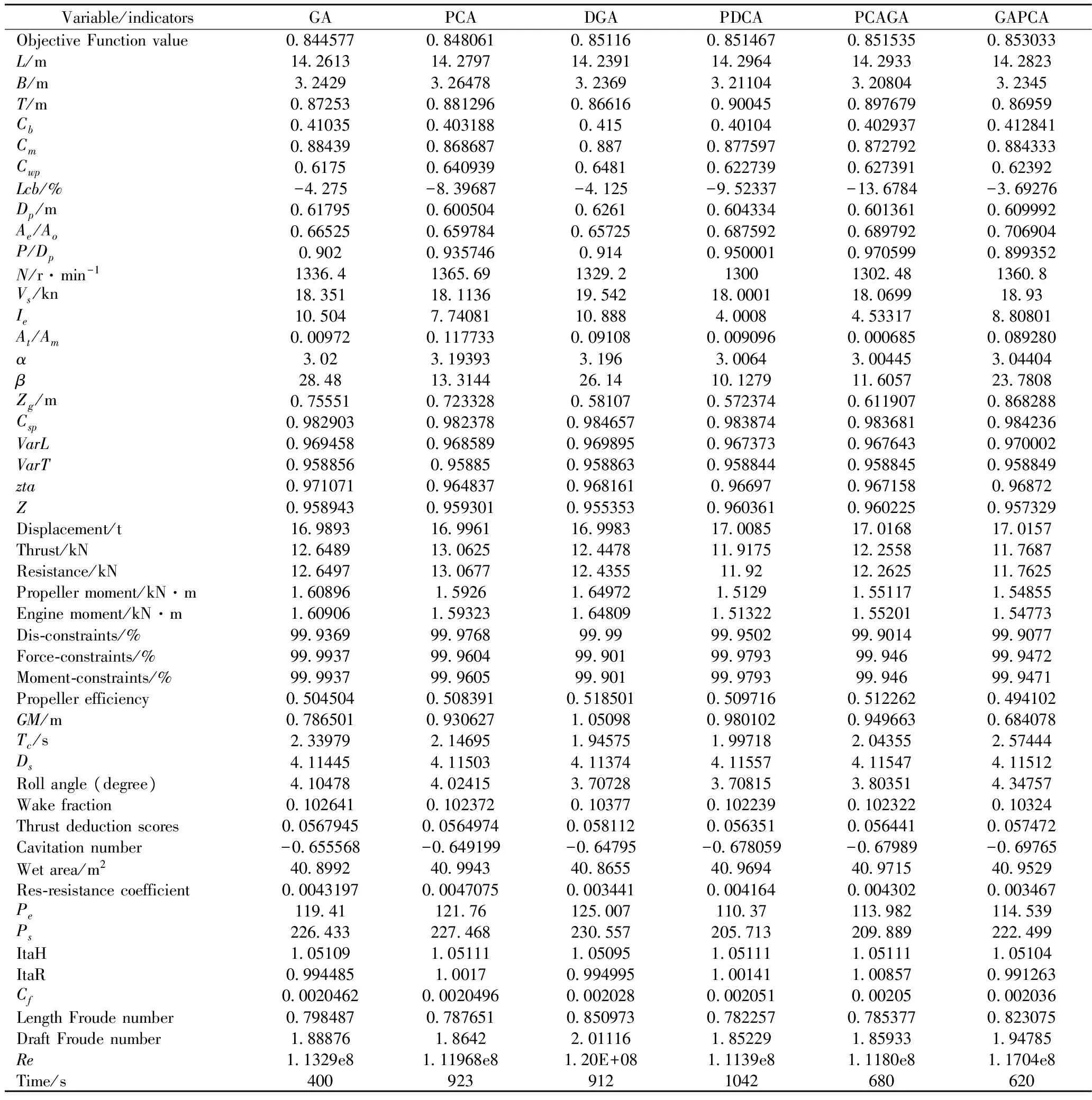
表2 不同優化方法的計算結果

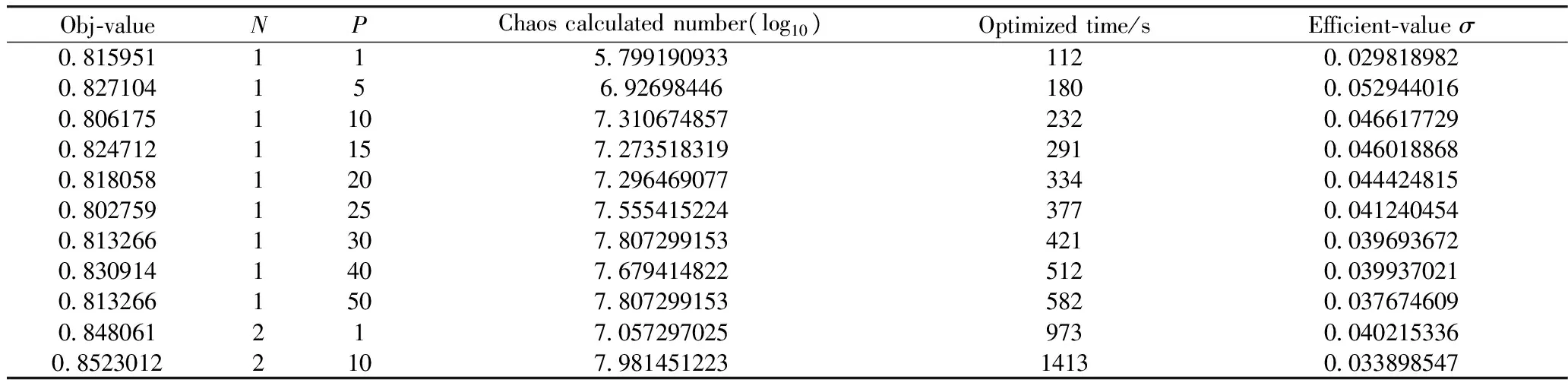
表3 混沌并行算法效率與并行次數N和區間混沌次數P關系表

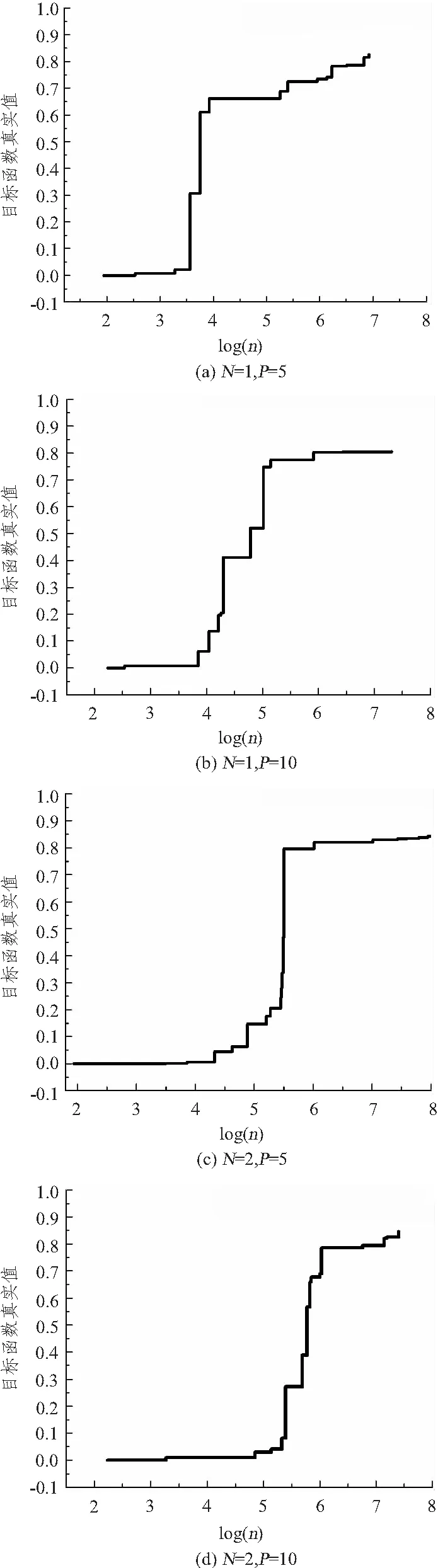
圖1 不同并行次數N和區間混沌次數P下目標函數 隨著混沌次數對數值變化圖Fig.1 Obj-function value increase by chaotic logarithm with different parallel number N and subspace chaotic value P

RatioscarriersDGACAGAGACA000110849465080617508514442084952608517790851492Improvement00072%56568%00056%00051085296508061750851950208532108512140852225Improvement00287%55868%00323%00110850065080617508505192085096008294830851099Improvement01053%28912%00682%00510849486080617508506362085172308270020852252Improvement02633%25834%01900%011085079108061750849951208525590828419085359Improvement02078%27592%04281%

3.2 結果分析

1)表1中遺傳算法一次載波遺傳代數為8 000次，并行混沌算法為混沌一次載波，并行次數取值為2，區間組混沌次數為1，混沌二次載波中第一次載波和并行混沌算法一致，在第二次載波中所選搜索域為原自變量區域的0.001，遺傳混沌算法采用遺傳算法為8 000代和混沌算法N=1，P=10，搜索域為原自變量區域的0.001，而混沌遺傳算法參數同遺傳混沌算法，但搜索區域為0.1，遺傳二次載波所選區域同樣為0.001。通過表1可以看出，6種優化算法的優化結果都比較好，各個約束都達到99%以上，遺傳的一次載波雖然搜索精度沒有其他6種算法的精度高，但是所花費的時間比較少；并行混沌一次載波和二次載波搜索精度相對于遺傳一次載波的有所提高，計算時間大大增加，效率因此會有所降低；遺傳算法二次載波在遺傳一次載波的基礎上繼續尋找最優值，但是所消耗時間比較多。遺傳混沌算法和混沌遺傳算法結合了2種算法優點，遺傳對變量范圍比較大的情況進行全局尋優能力比較強，而混沌對局部區域的尋優效果很明顯，在達到同樣的精度的情況下二者尋優所耗費時間比單一混沌算法或者遺傳算法少。

2)觀察表2，綜合優化算法的結果，綜合算法的搜索精度和搜索時間與計算次數，定義算法效率值：

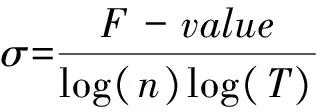
(8)

式中：n為混沌計算次數；T為計算時間；F-value為在對應n和T的情況下所搜索的最優函數值。對于混沌并行算法來說，在N=1的情況下，隨著P增加，搜索精度提高并不明顯，反而耗費的時間大大增加，效率值在P=5左右達到一個峰值，而當N=2時，搜索精度會很大程度上得到提高，但是效率值提高并不明顯。

3)觀察圖1，比較尋優函數值突增區域可以發現，隨著N的增加該區域會產生滯后，N=1、P=5時計算到3 500次目標函數值突增，N=2、P=5時計算到4 300次函數值突增，比較在P=10的2個圖像同樣出現了滯后增加現象。

圖2 優化提高比例隨二次搜索域比例變化圖Fig.2 Optimization improvement ratio with different secondary search domain

4)遺傳算法中全部取1 200代，比較不同二次載波搜索域比例對尋優的影響。二次搜索區域分別選取原區間的0.1%，0.5%，1%，5%，10%，分別選用遺傳二次載波、遺傳混沌算法和混沌遺傳算法3種算法比較兩次載波的尋優值，可以發現對于遺傳算法二次載波，隨著二次搜索區域的擴大，目標函數值優化提高的百分比出現增加，在5%的左右出現峰值，遺傳混沌算法的優化提高百分比一致增加，且增加幅度越來越大，混沌遺傳算法優化的目標函數值提高幅度卻隨著搜索域的增加而減少，混沌遺傳算法的二次載波最優值提高的幅度比例大大優于其他2種算法。

5)遺傳算法初始種群時是利用隨機數進行初始化，因此每次載波計算的結果都不相同，而混沌算法只要混沌初值一定，對應的混沌計算軌跡會一致。相對于選用混沌算法，第一次載波選用的遺傳算法可以降低優化陷入局部最優的可能性，以最快的速度找到最優值可能存在的區域，而合理的選取二次載波區域。如果選取混沌算法，利用混沌局部尋優的優點，可以在一定的時間內找到更好的最優值；如果選取遺傳算法，尋優效率沒有混沌算法高，計算時間長，且尋優值也低于混沌算法。

4 結 語

綜上所述，本文在一種高速單體無人艇數學模型的基礎上，應用上述6種算法進行了無人艇航行性能的優化計算，在達到同樣尋優精度的情況下，遺傳混沌算法和混沌遺傳算法的尋優效果都比單一的算法好得多，該方法為船舶優化設計提供了一種重要思路[6]。在船舶設計中，并不是所有的設計變量對船舶的綜合性能具有相同的重要性，有些設計變量存在平行關系和從屬關系，因此可以選取重要的設計變量進行優化計算，同時對于帶有系統可靠性設計的優化，怎樣構造帶有隨機性設計優化數學模型[7]，需要下一步的研究。

[1] YANG Song-lin,CHEN Shu-lin,ZHU Ren-qing,et al.A kind of design method of ship form parameters of large ship based on the best comprehensive performance[J].Ship Mechanics,2005,9(6):56-62.

[2] FENG Bai-wei,LIU Zhu-yuan,CHANG Hai-chao,et al.Study of multidisciplinary integrated optimization computing environment in ship design[J].Ship Mechanics,2009,20(2):5-8.

[3] TANG Zhen-mao,JIE De,MA Shi-hu,et al.Study of ship the conceptual design stage of multidisciplinary and multi-objective optimization[J].Ship Mechanics,2010,14(8):879-886.

[4] YANG Song-lin,CHEN Shu-lin,XI Wei,et al.Research of fuzzy chaos algorithm and its application in ship performance or structural characteristics comprehensive optimization[J].Ship Mechanics,2007,11(2):208-213.

[5] WU Yan,YANG Song-lin.Research of principal dimensions limited ship performance and structural features comprehensive optimization method[C].2009 Academic Conference Proceedings of the National High Performance Computing,2009:303-306.

[6] LU Chong-hong,LIN Yan,JI Zhuo-shang,et al.Application of genetic algorithms in the application of the calculation of ship free floating state[J].Journal of Shanghai Jiaotong University,2005,39(5):701-705,710.

[7] HAO Cui,OSMAN T.Application of a new multi-agent hybrid co-evolution based particle swarm optimization methodology in ship design[J].Computer-Aided Design，2010：1013-1027.

Parallel optimization method based on navigation performance of high-speed single hull ship

YU Qiang1,YANG Song-lin1,WANG Bao-ming1,YU Ning2

(1.Jiangsu University of Science and Technology, Zhenjiang 212003,China; 2.China Ship New Oasis Machinery Company,Nanjing 210012,China)

The optimization model is established including resistance and propulsion, maneuverability and seakeeping performance. Algorithms of GAPCA and PCAGA are developed while optimization program is written in C++ language in order to conduct optimization calculation based on the model, optimization ability research comparison of mixed algorithms of GAPCA and PCAGA and single algorithms of GA and CA are made while impacts of different secondary search domain ratios on objective function are studied, the conclusion is mixed optimization algorithm shows superior ability while different algorithms to find best objective value correspond to different secondary search domain ratios.

USV;navigation performance;comprehensive optimization;GAPCA;PCAGA

2013-05-20；

2013-07-01

俞強(1990-)男 ，碩士研究生，研究方向為水面高速船總體性能綜合優化方法、水下深潛器總體性能優化設計。

U661.1

A

1672-7649(2014)03-0040-06

10.3404/j.issn.1672-7649.2014.03.008