隨機因素作用下的超臨界Hopf分岔附近的動力學

李玉葉

（赤峰學院 數學與統計學院， 內蒙古 赤峰024000）

隨機因素作用下的超臨界Hopf分岔附近的動力學

李玉葉

（赤峰學院 數學與統計學院， 內蒙古 赤峰024000）

本文研究了確定的和隨機的INa,p+IK神經元模型中的超臨界霍普夫（Hopf）分岔附近的動力學行為，隨機模型中靠近Hopf分岔點的隨機節律被認為是整數倍節律模式；還研究了相應于分岔點附近的隨機自共振機制.結果不僅揭示了超臨界Hopf分岔點附近的神經放電的統計特征和動力學機制，還給出了實用于現實神經系統中Hopf分岔的判斷指標.

Hopf分岔；隨機自共振；神經放電模式；II型興奮

李玉葉，女，1980年7月生，內蒙古赤峰市人。2004年畢業于內蒙古大學理工學院數學系數理基地（數學），獲得理學學士學位；2009年畢業于內蒙古大學數學與統計學院應用數學專業，獲得理學碩士學位；2012年畢業于陜西師范大學生命科學學院生物物理專業，獲得理學博士學位。

研究方向：非線性動力系統的分岔與混沌理論及其應用，神經動力系統與復雜網絡動力學，神經信息傳遞與編碼。

1 引言

整數倍節律模式的放電現象最初是在實驗中被發現的.早在1967年，Rose[1]發現猴聽神經纖維表現這種較為異常的放電活動模式，但是，這一實驗現象很長時間內并未得到合理的解釋和引起大家的注意.隨后更多的實驗發現了類似的現象，如Douglass[2]在選擇小龍蝦水力敏感觸須的機械感受器作為實驗對象時，發現其放電節律模式呈現整數倍現象.這種具有“遺漏”現象的放電模式，在外周期刺激下的放電節律和放電尖峰的峰峰間期統計直方圖呈現出兩個特點：（1）多數峰峰間期是某一放電峰峰間期的整數倍；（2）峰峰間期統計直方圖是多模態的高峰狀,且隨著ISI的增大其出現的頻率呈降低的趨勢,如圖3（b）和（c）所示.

隨著隨機共振（stochastic resonance）概念被引入神經科學，整數倍節律的現象得到了研究，揭示了噪聲在神經信息處理中會起關鍵的正面作用；同時也揭示了整數倍的特征及動力學機制.在沒有外界周期信號激勵的情況下，現實生物的自發神經放電也發現了位于靜息和周期1節律之間的自發整數倍節律[3]；將隨機因素引入到確定性模型形成的隨機模型模擬了從靜息到整數倍放電再到周期1放電的過程[3]；而自發整數倍節律也被揭示為是經過隨機自共振(Autonomous stochastic resonance or coherence resonance)機制在Hopf分岔點附近產生的，也是現實神經系統中Ⅱ型興奮的自發放電的真實表現[3].

在本文中，基于實驗中神經起步點的整數倍節律[4,5]，通過噪聲對神經元INa,p+IK模型在超臨界Hopf分岔附近的作用，得到由隨機共振產生的整數倍節律，并對其產生的節律進行隨機共振分析.

2 INa,p+IK模型[6]及特性

此模型是與Morris-Lecar(ML)模型類似的模型，基于來自實驗的一個合理的假設：鈉的門控變量m(t)比膜電位V快，m(t)即時接近于m∞(V)的值.因此，令m=m∞(V)把三維系統簡化成二維系統，確定性INa,p+IK模型方程如下：

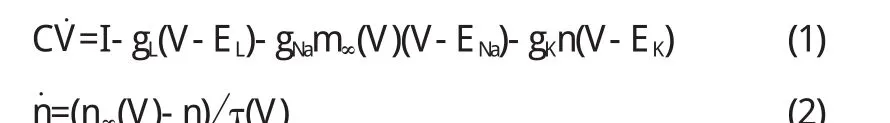
其中V是膜電位，I是膜電流，C膜電容，gNa、gK、gL分別是鈉電導、鉀電導和漏電導，ENa、EK、EL是相應的平衡電位，m∞(V)、n∞(V)分別是Na+離子通道和K+離子通道打開概率的穩態值，它們滿足如下方程：

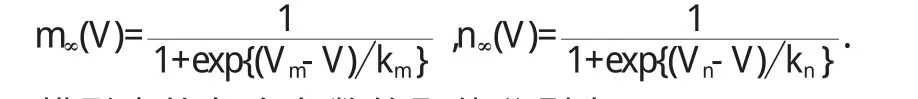
模型中的各個參數的取值分別為：C=1.0；EL=-78.0；gL=8.0；gNa=20.0；gK=10.0；Vm=-20.0；Vn=-45.0；Km=15.0；Kn=5.0；τ(V)=8.0；ENa=60.0；I=3.0；Ek為分岔參數.此時INa,p+IK模型為II興奮性的.時間單位msec.

引入高斯白噪聲ξ(t)作用到方程（1）式，方程（2）式不變，就形成了隨機INa,p+IK模型.白噪聲ξ(t)具有以下性質：(1)統計平均值為零，<ξ(t)>=0；(2)不同時刻的ξ(t)互不相關，<ξ(t) ξ(t')>=D2δ(t-t')，其中D是噪聲強度，δ(·)是Diract-δ函數.

在確定和隨機的INa,p+IK模型中，在數值模擬中，我們采用定步長Mannella算法[7]對微分方程組進行積分，其積分步長取0.001msec.

確定性INa,p+IK模型關于參數Ek的平衡點分岔圖，如圖1所示.當Ek<-88.216156系統存在一個穩定的不動點.在Ek=-88.216156發生了超臨界的Hopf分岔，有向右的穩定的如圖2所示.隨著參數Ek的繼續增加，Ek=-54.379639發生了亞臨界的Hopf分岔，同時有不穩定極限環產生，然后穩定極限環(粗實線)和不穩極限環(粗虛線)相碰發生了極限環的鞍結分岔，極限環消失，這里不予關注.極限環產生（黑實線代表極限環的最大幅值和最小幅值），

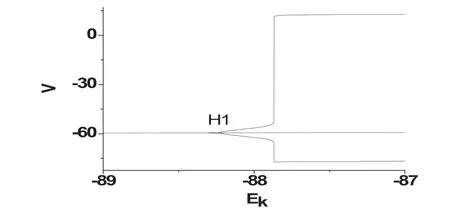
圖1 確定性INa,p+IK模型關于分岔參數Ek的平衡點分岔圖

3隨機INa,p+IK模型中的隨機放電節律

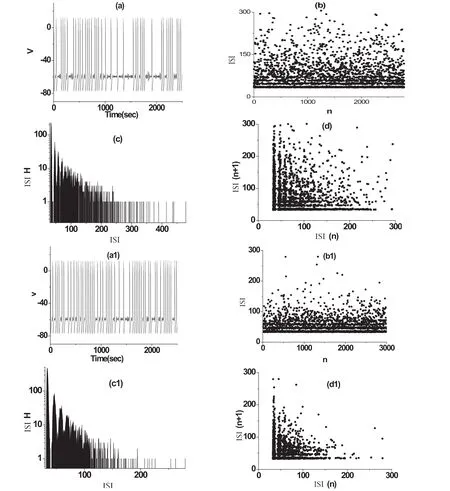
圖2 當不同Ek時，隨機INa,p+IK模型整數倍節律模式：（a）和（a1）是膜電位的時間歷程圖；（b）和（b1）是ISI的時間歷程圖；（c）和（c1）是ISI的統計直方圖；（d）和（d1）是ISI的回歸映射圖.其中（a）、(b)、(c)、(d)代表Ek=-88.5時，（a1）、(b1)、(c1)、(d1)代表Ek=-88時

在確定性INa,p+IK模型中，Ek=-88.5和Ek=-88時其行為為靜息態，無放電.在隨機INa,p+IK模型中，在引入合適的噪聲強度（D=0.5）時，會有非周期放電節律產生.其放電軌跡如圖2(a)和(a1)所示，看似是沒有規律的放電活動.其峰峰間期（ISI）序列，都具有明顯的分層現象，如圖2(b)和(b1)所示.其峰峰間期（ISI）統計分布圖標也為多峰態，隨著各模態的峰隨峰峰間期的增大而逐漸衰減，且大多數峰峰間期大約為第一模態峰峰間期的整數倍，如圖2(c)和(c1)所示.所以通過上述分析可以認為此隨機節律為整數倍節律，同時可以理解整數倍節律模式的膜電位的時間序列是在周期一與靜息交替出現，且靜息的長基本是周期一的整數倍；但在Ek=-88.5和Ek=-88時整數倍節律的區別是：在相同的噪聲強度下，當Ek=-88.5時的周期一放電比當Ek=-88時的放電偏少，主要原因有兩個：一是分岔參數距離分岔點的遠近問題，另一個是分岔參數所處的穩定極限環和平衡點的吸引域的大小問題.整數倍節律的峰峰間期序列雖都具有明顯的分層現象，但當Ek=-88.5（Hopf分岔點左）時的峰峰間期序列相對散，而當Ek=-88（Hopf分岔點右）時的峰峰間期序列主要集中在周期一放電.但兩者整數倍節律模式的峰峰間期序列的回歸映射都成晶格狀，如圖2(d)和(d1)所示.這些不僅體現整數倍的特征，還體現了在Hopf分岔點左、右得到的整數倍節律的區別，這不僅有利于我們模擬數據的選取，還有利于我們更好的了解整數倍節律產生的機制.

4 隨機INa,p+IK模型中的隨機自共振

由于隨機INa,p+IK模型系統含有噪聲項，所以由于噪聲的影響，在Hopf分岔附近有隨機共振現象產生.現取Ek=-88.5（Hopf分岔點左）為例說明，當噪聲強度為零時，初值取為(V,n)=（-60.46571，0.05226），系統處于閾下振蕩或者靜息態，如圖3(a)所示；當噪聲強度比較小時，神經元大部分時間在固定點(靜息電位)附近波動，只偶爾才激發，這是由噪聲超過閾值而造成的，如圖3(b)所示；當噪聲強度略為增大時，噪聲會激發神經元的發放，放電增多，如圖3(c)所示，而且，在幾個主要的頻率附近出現峰電位，這個頻率是頻譜圖最高峰處所對應的頻率，如圖3(d)所示.由圖3(b)和(c)可以看出，在噪聲強度較弱的情況下，膜電位的時間序列中的低閾值振蕩和稀疏的周期振蕩序列的間隔非常明顯.

圖3 當Ek=-88.5時，隨機INa,p+IK模型在不同噪聲強度下膜電位的時間歷程圖：（a）D=0；(b)D=0.05；(c)D=0.5；(d)隨機INa,p+IK模型在不同噪聲強度下功率譜

描述共振特征的一種常用手段是信噪比[8]，這里采用胡崗[9]在1993年提出的一個定義：

上式中H代表經過快速傅立葉變化后所得的頻率譜上峰的高度，ωp是峰高處對應的頻率（也被叫做基頻），Δω表示峰的半峰高度時的頻率寬度.

在處理內隨機共振情況時，信噪比還有另一種比較常用的定義，其定義如下

用公式（3）計算其信噪比，如圖4(a)所示，當Ek的值增大時，信噪比沒有大的變化，但對于每一條曲線（即Ek固定）上都存在一個最佳噪聲強度使得信噪比的值最大，且信噪比取最大值所對應的噪聲強度都約為D=10.這種共振性質也可以用另一種方式來描述，即用公式（4）計算其信噪比，如圖4(b)所示,當Ek的值增大時，信噪比沒有大的變化，但在每一條曲線（即Ek固定）上都存在一個最佳噪聲強度使得信噪比的值最大，且信噪比取最大值所對應的噪聲強度都約為D=10.上述兩種信噪比的計算方式都體現了隨機自共振（或相干共振）的特性.

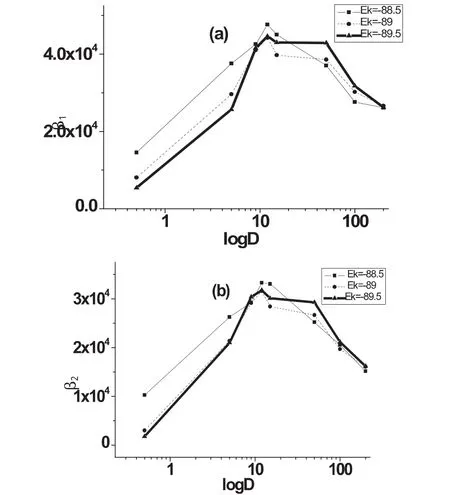
圖4 當Ek不同時，隨機INa,p+IK模型中通過功率譜計算β1、β2與噪聲D的關系圖：（a）是β1和logD的關系圖；(b)是β2和logD的關系圖

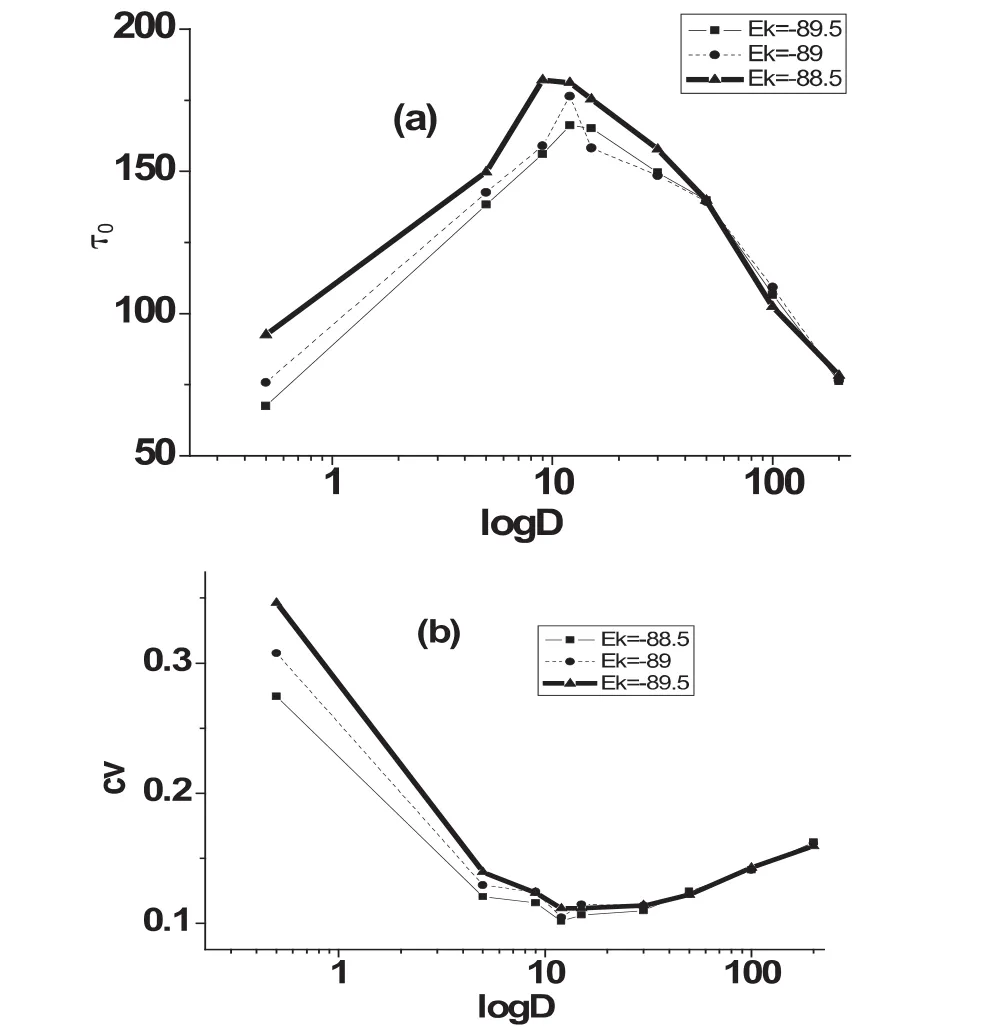
圖5 當Ek不同時，隨機INa,p+IK模型,(a)相關時間τ0與logD的關系圖;(b)變異系數CV與logD的關系圖

5 結論與討論

本文通過研究II型興奮對應的INa,p+IK模型中的超臨界Hopf分岔附近的自發放電節律的特征:ISI序列，回歸映射，ISI統計直方圖（含有指數衰減特征），ISI隨機序列的變異系數等，探討了在無外界的刺激下產生的隨機性整數倍節律模式.并且，整數倍節律模式存在于INa,p+IK模型的超臨界Hopf分岔附近的周期一與靜息之間.這與整數倍節律模式存在于Chay模型的亞臨界Hopf附近的周期一與靜息之間，而未出現于超臨界Hopf分岔附近的周一與靜息之間的結論[11]有些不一致.這是由于亞臨界Hopf分岔的共存區間特別小，它表現的性質與超臨界Hopf分岔的性質很接近的原因.還有并不是所有的超臨界Hopf附近都可以產生整數倍節律模式，由于整數倍節律模式必須有一個基本的放電頻率，所以我們選擇超臨界Hopf時選擇極限環變化比較穩定的較易出現整數倍節律模式.在本文中，隨機性整數倍節律模式都是高斯白噪激勵的隨機自共振現象.但其它噪聲也可以激勵出隨機自共振現象，如偽單色噪聲激勵的FHN模型可以在Hopf分岔點附近區域產生陣發周期一隨機共振現象[12].

〔1〕Rose J.E.,Brugge J.F.,Ardertson D.D.and Hind J.E.. Phase-locked response to low-frequency tones in single auditory nerve fibers of the squirrel mongkey[J]. Neurophysiol,1967,30:769.

〔2〕Douglass J.k.,W ilkens L.,PantazelouE.,Moss F.Noise enhancement of information Transfer in crayfish mechanoreceptors by stochastic resonance[J].Nature, 1993,365:337-340.

〔3〕Gu H.G.,RenW.,Lu Q.S.,W u S.G.,YangM.H.,ChenW.J. Integermultiplespiking inneuralpacemakersw ithoutexternal periodicstimulation[J].PhysLettA,2001,285:63～68.

〔4〕古華光，任維，楊明浩，陸啟韶.神經起步點產生一種新型簇放電節律-陣法周期1節律[J].生物物理學報,2002,18 (4):440-446.

〔5〕古華光，李莉，楊明浩，劉志強，任維.實驗性神經起步點產生的整數倍簇放電節律[J].生物物理學報,2003,19(1): 68-72.

〔6〕Izhikevich E.M.Dynam ical Systems in Neuroscience:The Geometry of Excitability and Bursting[M].The M IT Press, 2005.

〔7〕Mannella R.,Palleschi V.Fast and precise algorithm for computer simulation of stochastic differential equations[J]. Phys Rev A,1989,40:3381-3386.

〔8〕Benzi R.,Sutera S.,Vulpiani A.The mechanism of stochastic resonance[J].PhysA,1981,14:453～457.

〔9〕Hu G.,Ditzinger T.,N ing C.Z.Stochastic resonancew ithout externalperiodic force[J].PhysRev Lett,1993,71:807～810.

〔10〕Pikovsky A.S.,Kurth J.Coherence Resonance in a Noise-Driven Excitable System[J].Phys Rev Lett,1997, 78:775～778.

〔11〕楊卓琴.神經元模型放電節律模式的非線性動力學研究[D].北京:北京航空航天大學，2003.

〔12〕古華光.實驗性神經起步點的自發放電節律和心臟電活動的非線性動力學分析[D].北京:北京航空航天大學，2000.

Q42

A

1673-260X（2014）07-0003-04

內蒙古自治區自然科學基金面上項目資助（2012MS0103）