計算機輔助教學在《數學建模》課程中的運用
——赤峰學院《數學建模》教學心得體會

李玉葉，王曉英

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

計算機輔助教學在《數學建模》課程中的運用
——赤峰學院《數學建模》教學心得體會

李玉葉，王曉英

（赤峰學院 數學與統計學院，內蒙古 赤峰 024000）

《數學建模》是一門綜合利用數學知識和計算機技術解決實際問題應用性很強的課程，是培養學生綜合素質特別是數學應用能力的重要途徑.但該課程涉及的知識領域眾多，并且所研究的問題都來源于實際比較復雜，在授課中如果采用傳統的單一授課方式，會使學生感到枯燥，難于理解而失去學習的興趣，很難達到良好的效果.為了提高教學效率，要寓教于樂，運用計算機輔助的多種教學手段：運用現代化教學手段，提高學生對知識的理解；利用圖形結合，加強學生的直觀認識，培養學生運用所學知識的能力；親自建模、編程，課堂講授，發展學生的應用意識，培養實踐能力.通過這些計算機輔助手段的運用，使枯燥、難于理解、涉及面廣的《數學建模》課程變得形象、直觀、易接受，從而獲得了良好的教學效果.

《數學建模》； 課堂教學；教學手段

數學建模是利用數學方法解決實際問題的一種活動，是把數學知識與客觀實際問題聯系起來的紐帶.是培養學生綜合素質特別是數學應用能力的重要途徑.《數學建模》這門課的開設培養了學生的創新能力、想象力、洞察力、判斷力等，從而有效地體現了數學教育對于學生能力培養的重要作用.但在授課過程中，由于該門課程所涉及的領域廣泛，且所建模的問題幾乎來源于實際，因此，大多數情況下，涉及眾多理論及復雜的實際問題，從而使得該課程在某種程度上顯得索然無味，比較枯燥，大學生正處于思維活躍期，專注力持續時間有限，故而容易產生厭倦情緒，傳統的教學方法，很難保證讓學生持續專注，達到預期的目的.為了提高

《數學建模》這門課的教學的效率，使學生樂于學習，更好的掌握所學的知識，在該門課程的授課過程中，我們要突破以講授為主的傳統的教學手段，通過計算機輔助教學，采用多種教學手段，比如數形結合，圖形結合，動態切換，圖文并茂等，可以形象直觀的學到知識，產生深刻的印象，并獲得良好的教學效果.

1 運用現代化教學手段，提高學生對所學知識的理解能力

現代化的教學手段包括錄像、錄音、幻燈、投影、多媒體課件等影像資料，把這些直觀的、生動的運用到《數學建模》的課堂教學中，能有效地提高教學質量.

比如“數學規劃模型”這一節內容，對于根據實際問題所建的數學模型，其變量有十幾個甚至幾十個之多；除此之外，還有一些其他的約束條件.如此一來，變量參數多，計算量龐大，過程繁瑣，因此傳統的計算方法（如手工運算）求解比較困難.但對于該規劃問題的求解，如果采用LINGO軟件，就非常簡便.LINGO（Linear Interactive and General Optimizer即“交互式的線性和通用優化求解器”），它可以用于一些線性和非線性方程組的求解，也可以用于求解非線性規劃等，功能十分強大，是求解優化模型的最佳選擇.但學生對此軟件并不熟悉甚至沒有聽說過，更別提使用了.因此，為了提高課堂教學效果，我們借助多媒體課件首先給同學們介紹一下LINGO軟件的基本使用方法，然后選取不同實際事例，不同變量個數的數學規劃模型進行講解.

例如：在講授“奶制品的生產與銷售”這一節時我們建立規劃模型如下：

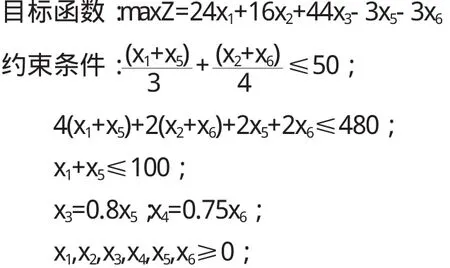
這是一個六個變量的線性規劃問題，用LINGO求解就比較方便，在LINGO下新建一個模型文件（即LINGO程序，一般以“LG4”為后綴名），書寫形式如下：

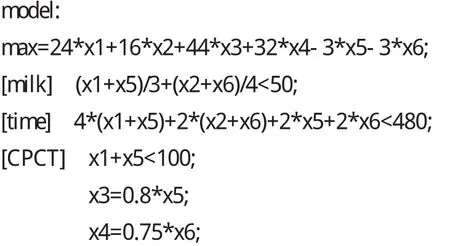
將文件存儲并命名后，選擇菜單“LINGO︳Solve”執行，即可得到如下的解：

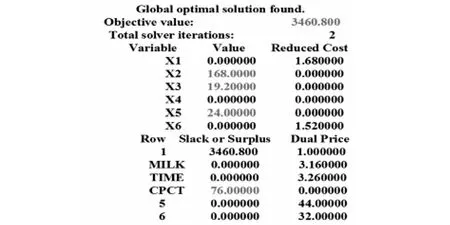
最優解為x1=0,x2=168,x3=19.2,x4=0,x5=24,x6=0,最優值為3460.8.通過計算機，可以輕松的改變變量，建立新的模型，從而更好地揭示規律.

2 利用圖形結合，加強學生的直觀認識，培養學生運用所學知識的能力

《數學建模》這門課程是近十幾年來開設的一門新課程，它以現實問題為載體，把數學知識、數學軟件和計算機應用有機的結合，融實用性、實踐性、知識性和創造性于一體，特別強調學生的主體地位，在教師的指導下，用所學的數學知識和計算機技術，借助于數學軟件，建立數學模型，分析、解決一些經過簡化的現實問題.但是對于實際問題往往很復雜，建立的數學模型，無法通過求解數學方程得到其解析解，所以只能借助數學軟件進行求解，將求得的數值解，用軟件畫圖，以圖的形式展現給學生，這樣加強學生的直觀認識，培養學生運用所學知識的能力.

例如，在講授傳染病模型SIR模型：

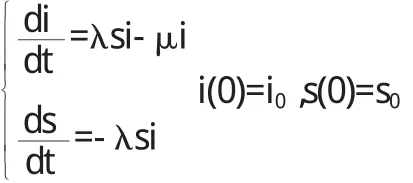
該方程無法求出s(t)和i(t)的解析解，我們只好求數值解，這就的借助于計算機軟件，我們通過多媒體課件展示數值求解的程序，如下：

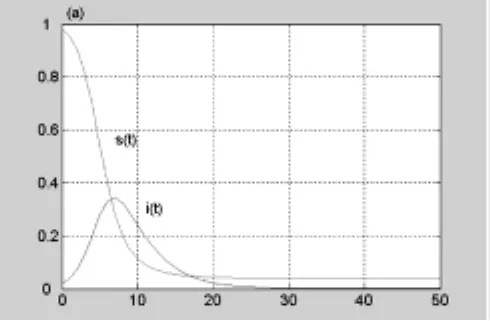
圖1 s(t)和i(t)關于時間t的圖

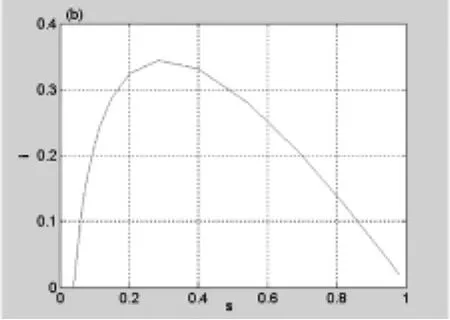
圖2 i：s圖形

3 親自建模、編程，課堂講授，發展學生的應用意識，培養實踐能力

《數學建模》這門課程不是為了建模而建模,開設數學建模課的目的是通過建模加深學生對數學知識的理解,掌握建模的思想方法,促進其他課程的教學,提高學生的綜合素質.因此在數學建模實踐課中，要充分發揮學生的主體作用，充分調動學生的主觀能動性，讓學生們結合學習生活中所遇到的問題，進行選題，建模，編程求解、回答原問題等，學生完成以上工作后，進行課堂講授、討論，通過大家的不同建議及意見，作進一步的修正，同時，在這一過程中，對于學生，老師是一個引導者，啟發者；而對于老師也是學習的過程，學習學生對這個問題的理解和認識；達到教學相長的相互有益的結果.在整個過程中，學生們要解決問題，必須善于深入地思考問題,迅速準確地把握問題的關鍵,揭開問題的本質,將現實問題抽象的化簡為數學問題,搞清楚問題的已知條件、未知條件和求解目標，并找出以上因素之間的聯系，建立模型.這個過程對于學生思維的深刻性和敏捷性得到了充分的鍛煉.由于學生所作的建模問題是一個沒有現成答案、模式的問題，所以他們在建立數學模型的過程中,充滿了大量的分析與綜合、猜側與嘗試、類比與聯想等的創造性活動,這就需要學生充分發揮想象力和洞察力,創造性地去解決問題.而且數學建模所得結果只是最優解答,并非唯一解答,這樣就給學生營造了一個可以充分發揮創造才能的空間.在完成了模型的建立、模型還得求解,實際問題抽象的數學模型往往很復雜，這就需要同學們自己編程借助軟件求解，提高了學生利用計算機處理問題的能力.將所得的計算結果學生必須“翻譯”回到現實問題中去,進行分析和檢驗.這是一個回顧和反思的過程，對于培養和訓練學生思維的批判性具有十分重要的作用.

總之，通過該學期計算機教學的課堂效果顯示，計算機輔助教學在數學建模課程中的作用是顯而易見的，同學們的課堂積極性，知識收獲程度，較上學期相比，有了很大的提升.通過計算機輔助的多種教學手段的運用，使枯燥、抽象、復雜的《數學建模》課程變得形象、直觀，也提高了同學們的學習興趣，從而獲得了良好的教學效果.

〔1〕姜啟源.數學模型[M].北京：高等教育出版社,1993.

〔2〕胡玉梅.高師院校數學建模課程建設的理論與實踐研究[D].天津師范大學,2003.

〔3〕劉來福，楊淳，黃海洋.數學建模方法與分析[M].北京：機械工業出版社,2009.

〔4〕嚴士健.數學思維與數學意識、創新意識、應用意識[J].教學與教材研究，1999.

G642

A

1673-260X（2014）10-0003-02

內蒙古自治區自然科學基金面上項目（2012MS0103）資助