基于主元分析與偏最小二乘故障診斷算法的研究
于 飛 王紅蛟
(青島科技大學自動化與電子工程學院,山東 青島 266042)
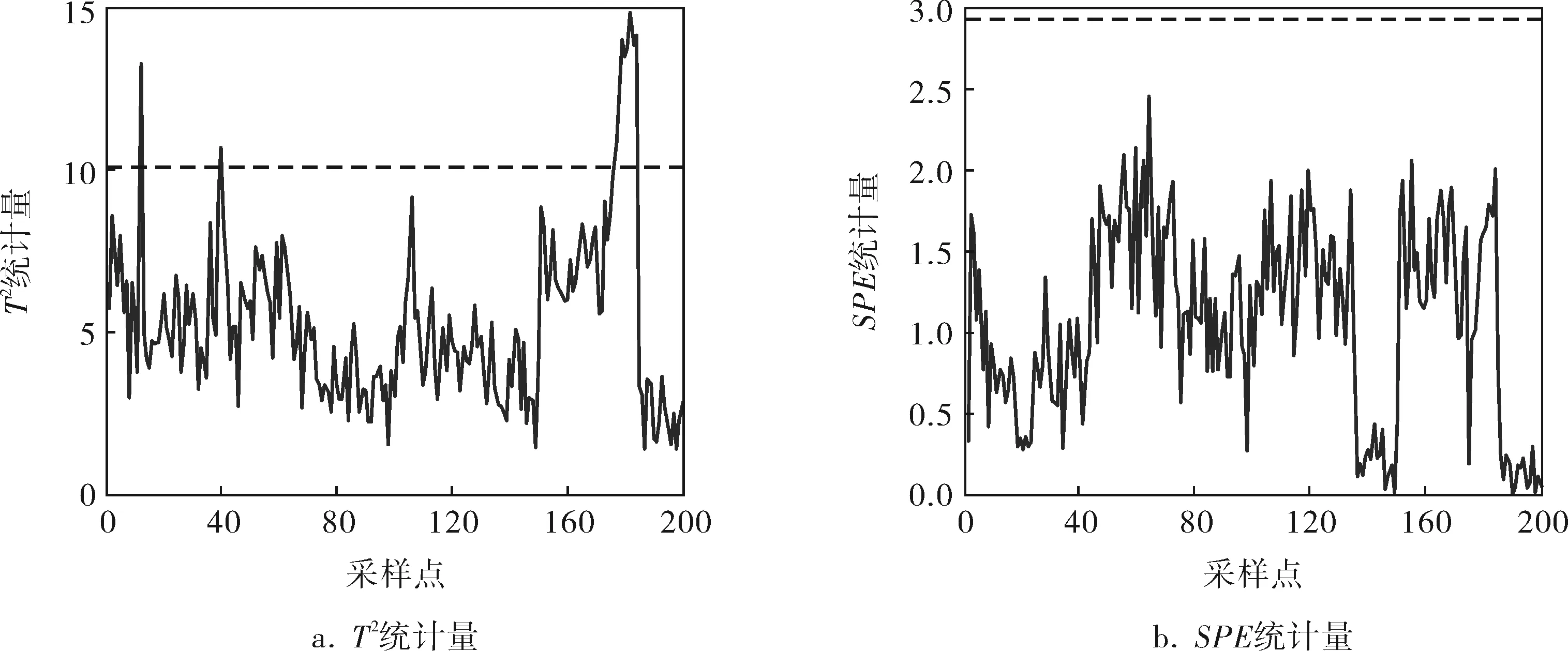
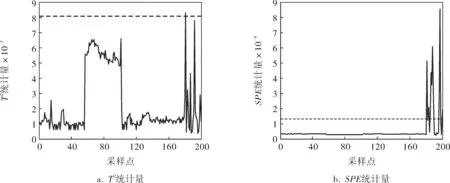
隨著計算機和電子測量技術的飛速發展,現代工業過程大都具有完備的傳感器裝置,可以在線獲得大量的過程數據。對這些數據進行統計分析可以幫助操作人員及時發現過程故障,避免重大事故的發生。目前,基于數據分析的故障檢測方法中應用最多的有主元分析、偏最小二乘及獨立元分析等。主元分析在故障診斷、數據壓縮、信號處理及模式識別等領域中均有廣泛的應用[1~3],該方法是依據線性變換,將數據從原始的n維空間映射到新的m維子空間上(m 假設所研究的監測過程有n個樣本,m個變量,將研究對象轉換為一個n行m列的矩陣Xn×m。對矩陣X中的每個變量進行標準化處理,標準化后的數據矩陣為: (1) 求得標準化后的數據矩陣X的協方差矩陣為: (2) 確定主元的個數時常用特征值方差累計貢獻率法,前k個主元累計貢獻率CPV可表示為: (3) 當前k個主元的累積貢獻率超過一個閾值時(閾值需根據實際情況確定,如85%),對應的k值就是需要保留的主元個數。由主元得分矩陣T=XP,可得主成分向量為: (4) 通過建立HotellingT2和預測誤差統計量(SPE)判斷過程是否發生故障。其方法是在主元子空間HotellingT2統計量進行統計檢驗;在殘差子空間中建立預測誤差統計量進行統計檢測[6]。SPE統計量也稱為Q統計量,即: (5) SPE統計量的控制限通過其近似分布來計算:當SPE≤SPEa時,系統運行正常;當SPE>SPEa時,系統出現故障。其中SPEa是檢驗水平a下的置信度,其計算式為: (6) h0=1-2θ1θ3/3θ2 式中Ca——正態分布在檢驗水平a下的臨界值; HotellingT2統計量通過主元模型內部的主元向量模的波動來反映多變量的情況,可以定義為: (7) (8) 式中F(l,n-l,a)——對應于檢驗水平為a、自由度為l和n-l條件下的F分布臨界點; Λ——前l個主元對應的特征值λ1,λ2,…,λl構成的l×l對角矩陣。 偏最小二乘法利用多變量輸入和多變量輸出組成的矩陣,通過矩陣的降維處理建立低維的輸入和輸出矩陣,再用線性回歸法建立自變量(輸入得分向量)與因變量(輸出得分向量)之間的內在線性關系[7]。收集正常流程的質量數據[8],建立自變量輸入矩陣X∈Rn×m和因變量輸出矩陣Y∈Rn×p,其中n是樣本點的個數,m是變量的個數,p是因變量的個數。偏最小二乘法把X和Y降維到一個低維空間,定義一個小數量的潛變量t1,…,tI,其中I是投影的隱潛在結構因素的個數。對X和Y均值中心化和標準化處理分解如下: (9) 其中,T=[t1,…,tI]是輸入的得分向量,P=[p1,…,pI]和Q=[q1,…,qI]分別為X和Y的載荷,E和F分別是X和Y的偏最小二乘殘差。潛在的得分向量ti的計算順序以輸入數據之間最大的協方差為標準,Xi=Xi-1-ti-1pi-1T,X1=X,輸出數據為Y。 通過判斷SPE統計量和T2統計量是否超過各自的控制限來檢測系統是否發生故障。T2、SPE統計監測的計算式分別為: t=RTX F(l,n-l)是以l和n-l為自由度的F分布,χh2是以h為自由度的χ2分布。其中SPE統計量的分布還可以按Jackson和Mudholkar的方法來近似計算[9]: 筆者采用分析離線數據的方法進行故障診斷,首先對鍋爐系統變量的離線數據進行預處理。筆者提取400個采樣點進行數據分析,分析前200個數據得到控制限,分析后200個數據進行故障診斷。用主元分析法對故障進行仿真,得到的T2和SPE統計結果如圖1所示;用偏最小二乘法進行故障診斷并建立回歸模型,找到各自變量(輸入)對因變量(輸出)的回歸關系,得到的故障檢測結果如圖2所示。 由圖1、2可以看出:在采樣點181~200添加一個變量引風調速閥位故障,兩種方法都可以診斷得出結果;但是,偏最小二乘法比主元分析法有較高的正確率,而且偏最小二乘法在進行故障診斷時對正常數據與故障數據的區分更有效,對于故障數據的識別率和靈敏度更高。 圖1 基于主元分析法的T2和SPE統計結果 圖2 基于偏最小二乘法的T2和SPE統計結果 利用主元分析法和偏最小二乘法對工業鍋爐故障進行診斷,通過仿真結果分析得出,偏最小二乘法比主元分析法有更高的正確率,對故障數據的識別率和靈敏性較高,并且能反映出線性回歸的方法建立自變量(輸入)與因變量(輸出)之間的關系。1 主元分析法及其故障診斷①
1.1 主元分析法的基本原理
1.2 基于主元分析法的故障診斷
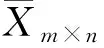

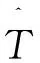
2 偏最小二乘法及其故障診斷
2.1 偏最小二乘法
2.2 基于偏最小二乘法的故障診斷
3 實例仿真
4 結束語

